zleti gazdasgtan Andor Gyrgy BME BME Ismtls 5

Üzleti gazdaságtan Andor György BME

BME Ismétlés › 5 Profit és a nettó jelenérték – 5. 1 Közgazdasági értelemben mi nem profit? – 5. 2 A számviteli és a gazdasági profit – 5. 3 A gazdasági profit forrásai – 5. 4 Profit a jövőben és a jelenre vetítve – 5. 5 Nettó jelenérték és a belső megtérülési ráta 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 2

6 Tőkejavak árazódása › Tőkejavak árazódási modellje vagy Tőkepiaci árfolyamok modellje – Capital Asset Pricing Model – CAPM BME 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 3

› Kockázat, kockázatkerülés, biztos egyenértékes, kockázati prémium, normális eloszlás, volatilitás… › E(F) és σ(F) › A kockázatos hozam is a normális eloszlással lesz megragadható. – A konstanssal osztás és kivonás nem változtat az eloszlás normalitásán (de a paraméterein természetesen igen). BME 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 4

› Mint már korábban megállapítottuk, a hatékonyan árazó tőkepiacon logikus kapcsolat kell legyen a biztos jelenbeli és a kockázatos jövőbeli pénzösszegek között. – A befektetők elvárt kamatait (hozamait) az időért és a kockázatért járó prémiumokra bontjuk fel: – Kockázatmentes kamat és kockázati hozamprémium › E(r. RP) „valahogy” a volatilitással függ majd össze, de hogy pontosan hogyan, ennek nem jártunk még a végére. BME 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 5
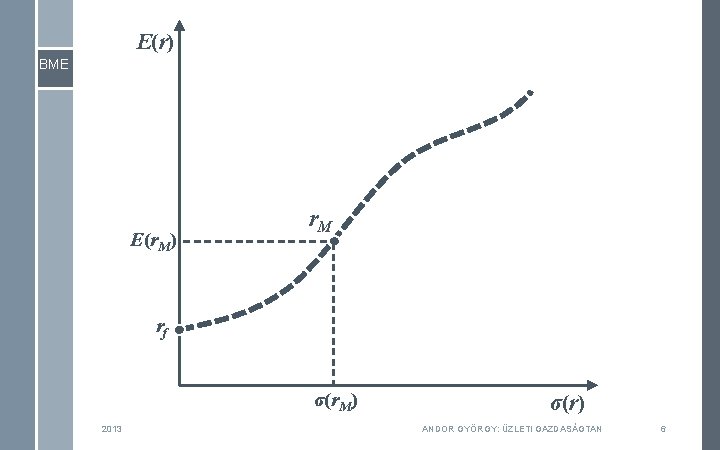
E(r) BME E(r. M) r. M rf σ(r. M) 2013 σ(r) ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 6

› Több időperiódus (év) esetén – Az időért járó prémium időben konzisztens. – A kockázatosságot okozó tényezők az üzleti világban időben állandó intenzitású véletlenséget okoznak. – Tehát az időt és a kockázatosságot egyszerre megragadó (egységnyi időre értelmezett) tőkeköltség állandó. BME 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 7

BME 6. 1 Várható hasznosság modellje › Bernoulli – A döntéshozó az egyes kimeneteleket nem a (várható) „matematikai” értékük szerint, hanem a (várható) hasznosságuk szerint súlyozva minősíti. – A döntési modellben tehát a várható hasznosság jelenik meg a várható értékkel szemben. – Ez a csökkenő határhasznosság elve miatt jelent alapvetően más megközelítést. › „A vagyon növekményének hasznossága fordított arányban lesz a már korábban birtokolt javak mennyiségével. ” › „Figyelembe véve az emberi természetet, úgy vélem, hogy a fenti hipotézis sokakra látszik érvényesnek. ” 2013 8
DANIEL BERNOULLI 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 9

SZENTPÉTERVÁRI PARADOXON Egy érmét addig dobálunk fel, amíg (például) fejet nem kapunk. A nyeremény összege 2 azon hatványa, ahányadikra sikerült fejet dobnunk. Egy ilyen játék várható értéke (várható nyereménye) végtelen: Az emberek viszont nem hajlandóak e játék lehetőségéért sokat fizetni… Hogyan magyarázná meg mindezt a várható hasznosság modelljével? 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 10

BME › Homo oeconomicusi döntés kockázatos helyzetekben – 1) Számba veszi a kockázatos választási lehetőségeket; – 2) Meghatározza e kockázatos lehetőségek lehetséges kimeneteleit (Fi) és ezekhez bekövetkezési valószínűségeket (pi) is rendel; – 3) Az összevethetőséghez (várható) hasznossági értéket E(U) rendel e kockázatos lehetőségekhez. 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 11

BME › A kockázatos helyzetekben való racionális viselkedéshez viszonylag összetett konzisztencia-követelményeknek kapcsolódnak. – Neumann János és Oskar Morgenstern › Játékelmélet, 1944 – Várható hasznosság modellje › Axiómarendszer › Képlet: 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 12

› Axiómarendszer BME – 1) A döntéshozó képes hasznosságuk szerint rangsorolni az egyes lehetséges kimeneteleket. (Összehasonlíthatóság axiómája. ) – 2) Amennyiben a döntéshozó A-t előnyben részesíti B-vel szemben, valamint B-t C-vel szemben, akkor A-t is előnyben fogja részesíteni Cvel szemben. (Tranzitivitás axiómája. ) – 3) A fenti A, B és C lehetőségeket tekintve mindig létezik (a legjobb) A-nak és (a legrosszabb) C-nek egy olyan valószínűségekkel súlyozott változata, amely mellett a döntéshozó közömbös lenne e változat és a B kimenet választása között. (Mérhetőség vagy folytonosság axiómája. ) 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 13

BME – 4) Amennyiben a döntéshozó A-t előnyben részesíti B-vel szemben, akkor előnyben fogja részesíteni az A p 1 valószínűséggel és B (1–p 1) valószínűséggel kombinációt az A p 2 és B (1–p 2) kombinációval szemben, ha p 1 > p 2. (Monotonitás axiómája. ) – 5) Az egyes lehetséges kimenetelek hasznosságai és bekövetkezésük valószínűségei egymástól függetlenek kell, hogy legyenek. (Függetlenség axiómája. ) › Ha ezek teljesülnek, akkor igaz, hogy 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 14

Ritka betegség, 600 áldozat AXIÓMÁK MEGSÉRTÉSE A: 200 -at megmentünk B: 33% senki nem hal meg, 67% mindenki meghal (72% az A-ra voksolt) C: 400 meghal D: 33% mindenki túléli, 67% senki sem menekül meg (78% D-t választotta) 5% munkanélküliség ~ 95%-os foglalkoztatottság 40$-os színház jegy A: Korábban megvesszük, de elvesztjük B: Előadás előtt vennénk, de észrevesszük, hogy elvesztettünk 40$-t Az A esetben inkább hazamegy…. 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 15
![A : [10. 000 € (100%)] ALLAISPARADOXON B : [15. 000 € (90%); 0 A : [10. 000 € (100%)] ALLAISPARADOXON B : [15. 000 € (90%); 0](http://slidetodoc.com/presentation_image_h/279c493c05b9040ee11bc099f4225a20/image-16.jpg)
A : [10. 000 € (100%)] ALLAISPARADOXON B : [15. 000 € (90%); 0 € (10%)] A többség A-t választja (pedig a B várható értéke 13. 500). C : [10. 000 € (10%); 0 € (90%)] D : [15. 000 € (9%); 0 € (91%)] Itt a többség D-t választja. Pedig 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 16

Két urna: ELLSBERG- PARADOXON 1) száz db piros és fekete golyó, ismeretlen arányban 2) száz db piros és fekete golyó, fele-fele arányban Egy urna és egy szín választás, ha talál: 100 €, ha nem: 0 €. A színekkel kapcsolatosan indifferensek voltak, viszont az urnákkal kapcsolatosan nem: többségük ragaszkodott a második urnához. 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 17

› Szubjektív valószínűség BME 2013 18

Bernoulli: „A találgatás művészete” › A valószínűség – matematikai értelemben – nagy számban ismétlődő események relatív gyakoriságának határértéke. Laplace: „A valószínűségek analitikai elmélete” Gauss: „Mi a valószínűsége, hogy…” Keynes: „Értekezés a valószínűségről” Jacob Bernoulli Pierre-Simon Laplace Friedrich Gauss A közgazdaságtanban a sokszori ismétlődés – legtöbbször – értelmezhetetlen. – Kockadobás eredménye vs. zöldmezős beruházás eredménye – Jövőre vonatkozó kérdések – Ott és akkor körülmények – Múltbeli adatok (nem is „ugyanarról”) M. Keynes 2013 ANDOR GYÖRGY: ÜZLETI GAZDASÁGTAN 19

› Szubjektív valószínűség BME – Amennyire a hasznosság is szubjektív, úgy gyakran a valószínűség is. – Az események bekövetkezési valószínűségeit nem mindig tudjuk objektíven meghatározni. › Csak ha pontosan ismerjük a valószínűségi szerkezetet. › Ha nem, ami egyáltalán nem ritka helyzet, kénytelenek vagyunk „csak” szubjektív valószínűség becslésekre hagyatkozni. › Ezek viszont inkább csak az események bekövetkezésével kapcsolatos meggyőződések, „hitek” mértékei, és nem objektív, statisztikai vagy valószínűségelméleti alapú döntési paraméterek. 2013 20
- Slides: 20