Zklady terie pravdepodobnost 1 asto sa hovor e

Základy teórie pravdepodobností 1

Často sa hovorí, že štatistika je “aplikovaný počet pravdepodobností” Štatistika popisná - vyčerpávajúce skúmanie (veda o štáte, popisná aritmetika) induktívna - výberové skúmanie (štatistické analýzy, výberové vzorky) Most medzi oboma druhmi štatistiky tvorí teória pravdepodobnosti • tvorí teoretický základ pre posudzovanie spoľahlivosti a presnosti výberových postupov 2

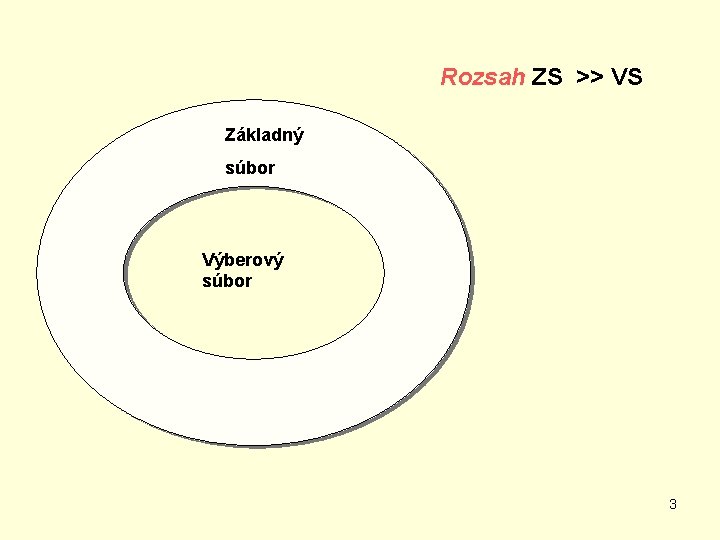
Rozsah ZS >> VS Základný súbor Výberový súbor 3

ZÁKLADNÉ POJMY TP: Náhodný jav, je jav ktorý ako výsledok určitého pokusu (komplexu podmienok) môže alebo nemusí nastať. Označujeme veľkými písmenami zo začiatku abecedy A, B, C. . Extrémnymi prípadmi javov je jav istý a jav nemožný. Jav istý (I)je taký jav ktorý ako výsledok daného pokusu nastane vždy. Jav nemožný (O)je taký jav ktorý ako výsledok pokusu nemôže nastať nikdy. Pravdepodobnosť je číselná miera možnosti nastatia náhodného javu 4

KLASICKÁ definícia pravdepodobnosti (Pierre Simon Laplace) n. . Počet všetkých možných výsledkov pokusu m. . . Počet výsledkov pokusu v ktorých jav A nastane (priaznivé výsledky). ŠTATISTICKÁ definícia pravdepodobnosti (Richard von Mises) Táto definícia je spojená s pojmon relatívnej početnosti, kedy pri malom počte pokusov má relatívna početnosť náhodný charakter. S rastúcim počtom pokusov sa však stabilizuje a približuje k určitému číslu (pravdepodobnosti). 5

Quetélet meral obvod hrude 5738 škótskych vojakov 6

Základné vlastnosti pravdepodobnosti Pravdepodobnosť, ako číselná miera možnosti nastatia náhodného javu, má niektoré dôležité vlastnosti: 1. Pre každý náhodný jav A platí: 2. Pravdepodobnosť javu istého I ( jav, ktorý ako výsledok náhodného pokusu nastane vždy ) je rovná jednej: 3. Pravdepodobnosť javu nemožného 0 ( jav, ktorý ako výsledok náhodného pokusu nikdy nenastane) je rovný nule: . 4. Pravdepodobnosť javu opačného k javu sa rovná: 7

Náhodný jav charakterizuje výsledok náhodného pokusu kvalitatívne (slovne). V mnohých prípadoch je však výhodnejšie charakterizovať výsledok kvantitatívne (číselne), k čomu používame náhodnú premennú. Náhodná premenná je taká premenná, ktorá môže nadobúdať rôzne hodnoty, alebo hodnoty z rôznych intervalov v závislosti na náhode. Náhodné veličiny budeme označovať veľkými písmenami s konca abecedy X, Y, Z a ich konkrétne hodnoty: xj, j=1, 2…n Na štatistické znaky môžme pozerať ako na náhodné premenné NP………. Členenie NP: § diskrétne (DNP) -nadobúdajú izolované, väčšinou celočíselné hodnoty, napr. počet narodených chlapcov z 1000 narodených detí, počet chybných výrobkov…. § spojité (SNP)-môžu nadobúdať ľubovoľné hodnoty z ohraničeného, alebo neohraničeného intervalu, napr. : hmotnosť, výška človeka, chyby merania v mm, príjem. . . 8

Náhodná premenná je plne popísaná zákonom rozdelenia NP Zákon rozdelenia náhodnej premennej je pravidlo pomocou, ktorého definujeme obor hodnôt NP a pravdepodobnosti s ktorými tieto hodnoty nadobúda. Môže byť vyjadrený rôznymi formami q pravdepodobnostná tabuľka, alebo rad rozdelenia q distribučná funkcia q funkcia hustoty pravdepodobnosti q DNP má dve formy zákona rozdelenia: –- pravdepodobnostná tabuľka, alebo rad rozdelenia –- distribučná funkcia q SNP má dve formy zákona rozdelenia: – distribučná funkcia – funkcia hustoty pravdepodobnosti 9

Pravdepodobnostná tabuľka- rad rozdelenia pravdepodobností - popisuje len diskrétnu náhodnú premennú (DNP), je najjednoduchšou formou zákona rozdelenia xi x 1 x 2 . . . xn Spolu pi p 1 p 2 . . . pn 1 V prvom riadku tabuľky sú uvedené všetky možné hodnoty diskrétnej premennej a druhom riadku im zodpovedajúce pravdepodobnosti 10

Distribučná funkcia je univerzálnejšou formou vyjadrenia zákona rozdelenia, slúži k popisu tak diskrétnej ako aj spojitej NP. Každému reálnemu číslu priraďuje pravdepodobnosť, že NP nadobudne hodnotu menšiu než toto číslo tj. : F(x) = P(X x) Každá distribučná funkcia má tieto základné vlastnosti 1. , tj. distribučná funkcia nadobúda hodnoty od nuly do jednej vrátane. 2. a 3. Distribučná funkcia je neklesajúca tzn. : ak 4. 5. Distribučná funkcia je spojitá zľava. Graf distribučnej funkcie zodpovedá v popisnej štatistike grafu kumulatívnych relatívnych početností. 11

Distribučná funkcia DNP Distribučná funkcia SNP 12

Funkcia hustoty pravdepodobnosti Pre spojitú náhodnú premennú je možné definovať zákon rozdelenia pomocou funkcie hustoty pravdepodobnosti f(x), alebo stručne hustota NP Funkcia hustoty pravdepodobnosti má tieto základné vlastnosti: 1. 2. 3. 4. 13

F(x) 14

Charakteristiky náhodných premenných Koncentrovaný popis rozdelenia náhodných premenných využíva (podobne ako v popisnej štatistike), číselné hodnoty, ktoré nazývame charakteristiky náhodných premenných. Najčastejšie používanými charakteristikami sú stredná hodnota, popisujúca polohu (úroveň) náhodnej premennej a rozptyl popisujúci variabilitu náhodnej premennej Pre DNP Pre SNP 15

Rozptyl je mierou variability náhodnej premennej, pričom ho môžeme všeobecne definovať v tvare: Pre DNP Pre SNP Pri popise náhodných premenných, najmä spojitých, sa veľmi často používajú tiež kvantily: p % kvantilom náhodnej premennej X, ktorá má spojité rozdelenie s distribučnou funkciou a hustotu pravdepodobnosti je číslo , pre ktoré platí: kde 16

Najčastejšie používané rozdelenia náhodných premenných Rozdelenia spojitej NP Diskrétne rozdelenia NP 1. 2. 3. 4. Alternatívne rozdelenie Binomické rozdelenie Poissonovo rozdelenie Hypergeometrické rozdelenie a iné 1. Normálne rozdelenie 2. Normované normálne rozdelenie 3. Rovnomerné rozdelenie 4. Exponenciálne rozdelenie 5. Weibullovo rozdelenie 6. Gama rozdelenie 7. a iné Výberové rozdelenia • chí- kvadrát rozdelenie • Studentovo t – rozdelenie • F- rozdelenie 17

Rozdelenia diskrétnej náhodnej premennej Alternatívne rozdelenie Náhodná premenná X má alternatívne rozdelenie s parametrom , kde , a ak nadobúda len dve hodnoty x = 0, a x = 1 a to s pravdepodobnosťami a , kde . Stredná hodnota alternatívneho rozdelenia je a rozptyl Uvedenú náhodnú premennú nazývame nula – jedničková, v praxi sa používa pri popise výskytu určitého javu. 18

Binomické rozdelenie Predpokladajme, že určitý pokus opakujeme n- krát za tých istých podmienok ( tj. takých pokusov, kedy výsledok žiadneho pokusu neovplyvní pravdepodobnosť výsledkov iných pokusov), pri ktorých môže nastať jav A s pravdepodobnosťou p, a nenastane s pravdepodobnosťou Pravdepodobnosť, že sa jav A objaví práve k- krát, je daná vzťahom: kde k = 0, 1, 2, . . . , n Hodnoty n a p sú parametre binomického rozdelenia tj. také veličiny, ktoré musíme poznať, aby sme mohli ľubovoľnému X priradiť jeho pravdepodobnosť. Pre strednú hodnotu a rozptyl náhodnej premennej s binomickým rozdelením platí 19

Poissonovo rozdelenie Predpokladajme, že počet pokusov n je dostatočne veľký (stačí ) a pravdepodobnosť p je veľmi malá (prakticky ), potom môžeme binomické rozdelenie aproximovať Poissonovým rozdelením s parametrom Pravdepodobnostná funkcia Poissonovho rozdelenia je daná vzťahom Kde k = 0, 1, 2, . . . Pre strednú hodnotu a rozptyl náhodnej veličiny s Poissonovým rozdelením platí ich rovnosť, tj Poissonovo rozdelenie tým lepšie aproximuje binomické rozdelenie, čím väčší je počet pokusov n a čím menšia je pravdepodobnosť p Riadi sa ním počet javov v priestorovej jednotke alebo počet udalostí v časovej jednotke. Niekedy sa zvykne Poissonovo rozdelenie označovať ako zákon vzácnych resp. zriedkavých javov. Príkladom môže byť počet výskytov vzácneho ochorenia zvierat, výskyt porúch strojného zariadenia 20 v čase t, a pod.

Hypergeometrické rozdelenie Predpokladajme, že v súbore N prvkov ich M má určitú vlastnosť A. Zo súboru náhodne vyberieme n prvkov, bez toho aby sme ich vracali späť do pôvodného súboru ( tzv. výber bez opakovania ). Počet prvkov s vlastnosťou A , ktoré boli vybrané do výberu prvkov je zrejme náhodná premenná X, ktorá môže nadobúdať hodnoty s pravdepodobnosťami Ak je rozsah výberu príliš malý vzhľadom na rozsah základného súboru , je možné hypergeometrické rozdelenie úspešne nahradiť binomickým rozdelením. V praxi sa často vyskytuje tiež aproximácia hypergeometrického rozdelenia Poissonovým rozdelením s parametrom náhrada je kvalitná už pri a . Hypergeometrické rozdelenie sa využíva v teórii výberových šetrení a štatistickej kontrole akosti 21.

Rozdelenia spojitej náhodnej premennej Normálne rozdelenie (Gaussovo) Normálne rozdelenie má v štatistike kľúčové postavenie, slúži ako pravdepodobnostný model chovania veľkého počtu náhodných javov v biológii, technike i ekonómii. Normálne rozdelenie je vhodným pravdepodobnostným modelom takých náhodných premenných, ktoré sú súčtom veľkého počtu nezávislých alebo len slabo závislých veličín ( zložiek ) Veľký význam normálneho rozdelenia je aj v tom, že za určitých podmienok je možné pomocou neho aproximovať rad iných spojitých i nespojitých rozdelení. Uvedeným podmienkam vyhovuje mnoho dôležitých premenných, s ktorými sa v praxi často stretávame napr. : úroda tej istej rastliny na rôznych pozemkoch, výška, hmotnosť, chyby merania a iné. Hustota pravdepodobnosti normálne rozdelenej náhodnej premennej je daná vzťahom: kde konštanty a sú parametre normálneho rozdelenia, kde je stredná hodnota, charakterizujúca polohu tohto rozdelenia, a je jeho rozptyl. 22

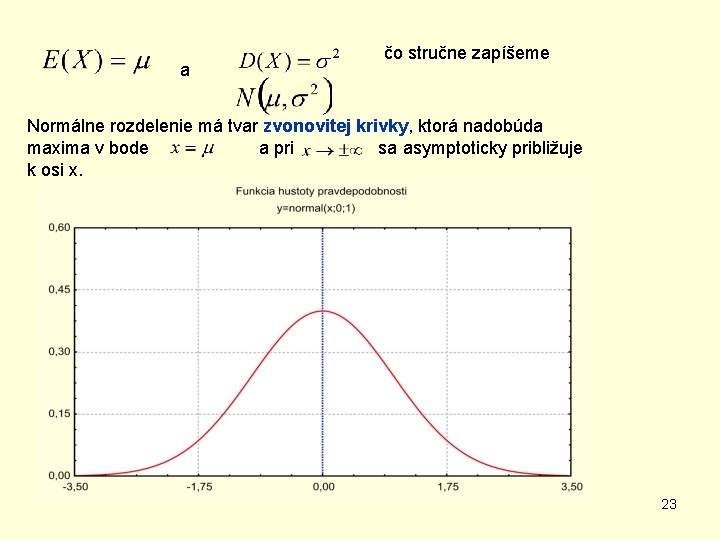
a čo stručne zapíšeme Normálne rozdelenie má tvar zvonovitej krivky, ktorá nadobúda maxima v bode a pri sa asymptoticky približuje k osi x. 23

Pre distribučnú funkciu normálneho rozdelenia platí vzťah: 24

Normované normálne rozdelenie Parametre normovaného normálneho rozdelenia sú resp. , normovaná náhodná premenná U má teda normálne rozdelenie so strednou hodnotou 0 a rozptylom 1, čo stručne zapíšeme N(0, 1). Stačí teda poznať normované normálne rozdelenie N(0, 1), pomocou ktorého s využitím transformácie popíšeme akékoľvek normálne rozdelenie Každé normálne rozdelenie je možné pomocou transformácie U upraviť na normované N(0, 1) Hustota pravdepodobnosti je symetrická okolo nuly, preto platí: 25

Častou úlohou pri aplikácii normálneho rozdelenia je nájsť pravdepodobnosť toho, že náhodná premenná X nadobudne hodnoty z intervalu x 1 až x 2. Pri výpočte tejto pravdepodobnosti využívame normovanie takto: z vlastnosti distribučnej funkcie vyplýva : Podobne postupujeme aj pri výpočte pravdepodobnosti toho, že náhodná premenná X je menšia než vopred zvolená konštanta x 26

27

- -2 -3 68, 26% 95, 45% 99, 73% + +2 +3 28

Typ rozdelenia Rovnomerné Parametre E(X) D(X) Hustota pravdepodobnosti Distribučná funkcia a, b Exponenciálne a, b, c Weibullovo Gama a, b a. b 29

Výberové rozdelenia S normálnym rozdelením sú úzko spojené tri dôležité rozdelenia spojitých náhodných premenných: chí- kvadrát rozdelenie , Studentovo t – rozdelenie a F- rozdelenie. Majú mimoriadny význam pri analýze štatistických údajov, získaných náhodným výberom - rozdelenie Ak sú , nezávislé náhodné premenné, z ktorých každá má normálne rozdelenie N(0, 1), potom súčet štvorcov týchto náhodných premenných, tj. premenná: má - rozdelenie s v stupňami voľnosti. Počet stupňov voľnosti je daný počtom nezávislých sčítancov, a je jediným parametrom tohto rozdelenia. Kvantily tohto rozdelenia je možné bežne vyhľadávať v tabuľkách resp. vypočítať s pomocou dostupného štatistického softwaru. Má rozsiahle použitie v teórii odhadu, testovaní štatistických hypotéz, pri overovaní nezávislosti kvalitatívnych znakov. . . 30

31

► Studentovo t-rozdelenie Nech sú nezávislé náhodné premenné, z ktorých a -rozdelenieso stupňami voľnosti . má normálne rozdelenie N(0, 1) a Z má Náhodná premenná : má Studentovo t- rozdelenie s v stupňami voľnosti. Počet stupňov voľnosti je jediný parameter tohto rozdelenia. Stretávame sa s ním v matematickej štatistike - odhady, testy hypotéz. . 32

F - rozdelenie Ak uvažujeme dve nezávislé náhodné premenné a s rozdelením a a stupňami voľnosti, potom náhodná premenná : má F - rozdelenie s a stupňami voľnosti, čo sú zároveň aj dva parametre tohto rozdelenia Stretávame sa s ním v matematickej štatistike - testy hypotéz, ANOVA. . 33