ZeroSkew Trees ZeroSkew Tree rooted tree in which

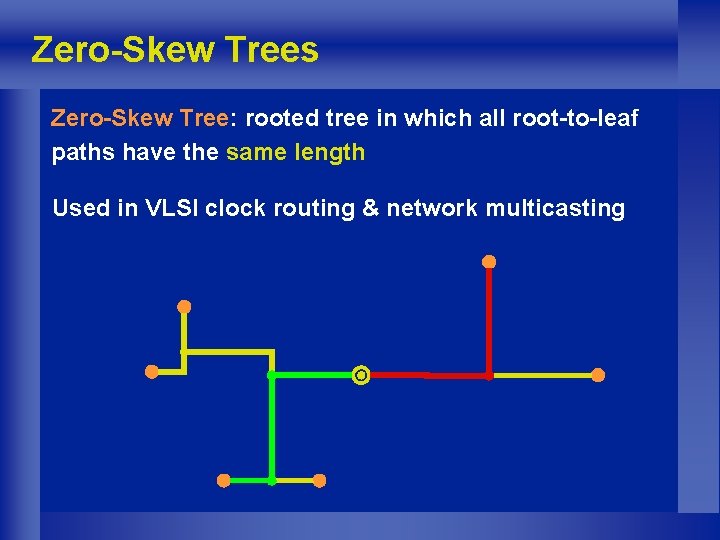
Zero-Skew Trees Zero-Skew Tree: rooted tree in which all root-to-leaf paths have the same length Used in VLSI clock routing & network multicasting

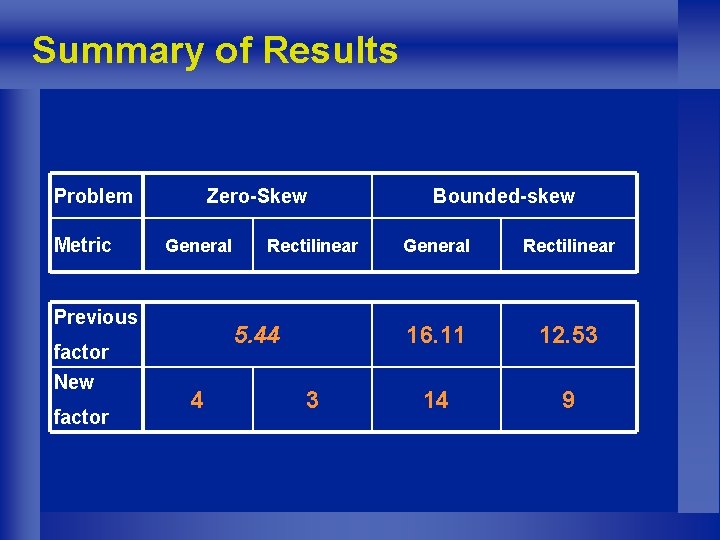
The Zero-Skew Tree Problem Given: set of terminals in rectilinear plane Find: zero-skew tree with minimum total length Previous results [CKKRST 99] • NP-hard for general metric spaces • factor 2 e ~ 5. 44 approximation Our results: • factor 4 approximation for general metric spaces • factor 3 approximation for rectilinear plane

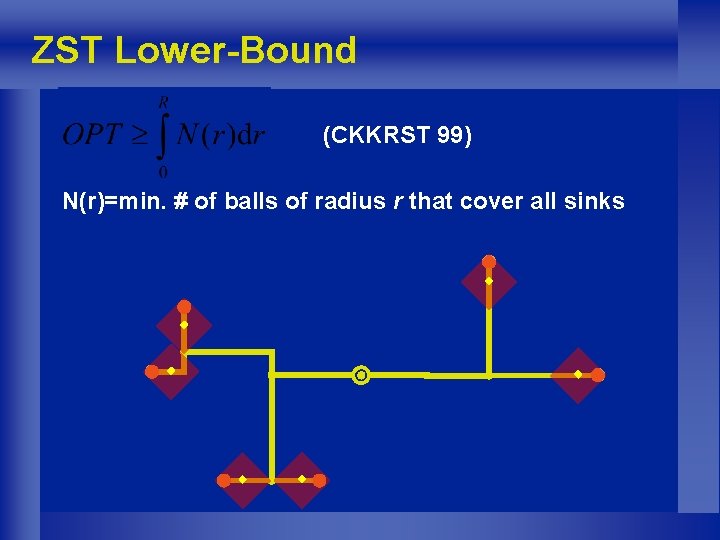
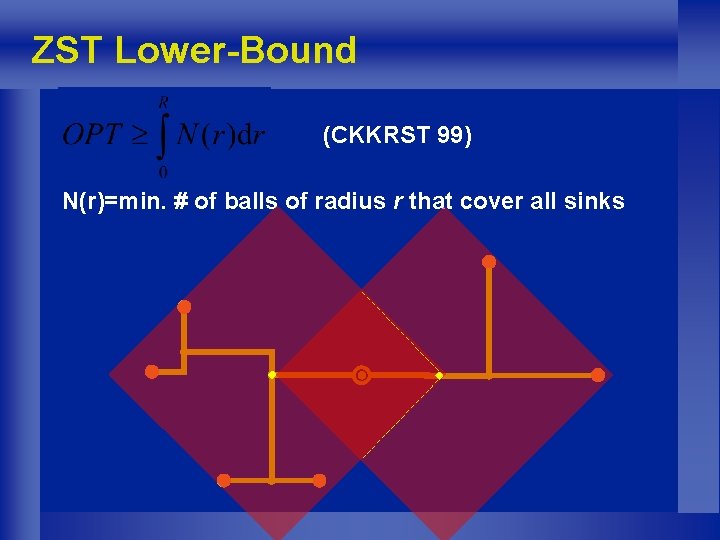
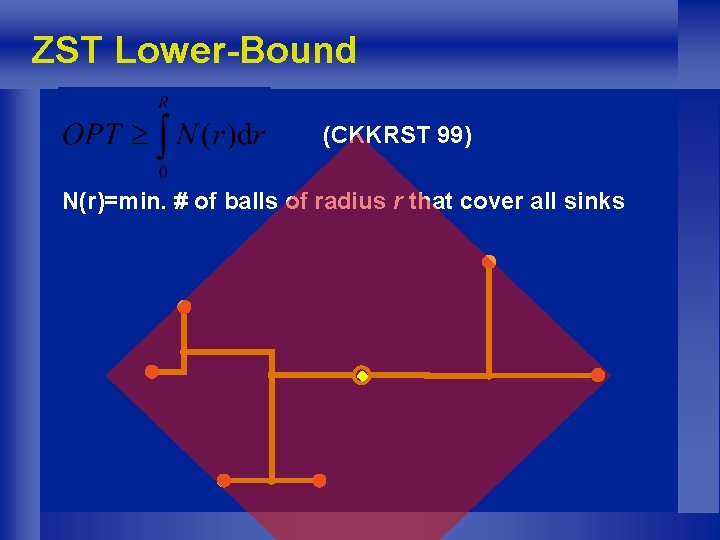
ZST Lower-Bound (CKKRST 99) N(r)=min. # of balls of radius r that cover all sinks

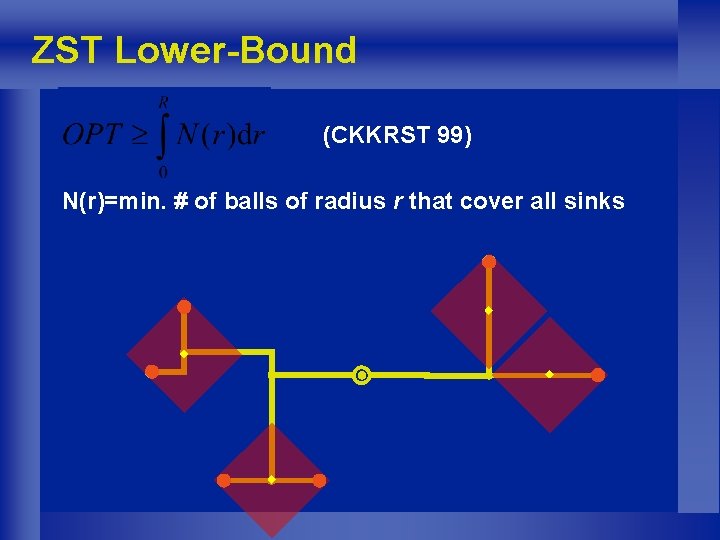
ZST Lower-Bound (CKKRST 99) N(r)=min. # of balls of radius r that cover all sinks

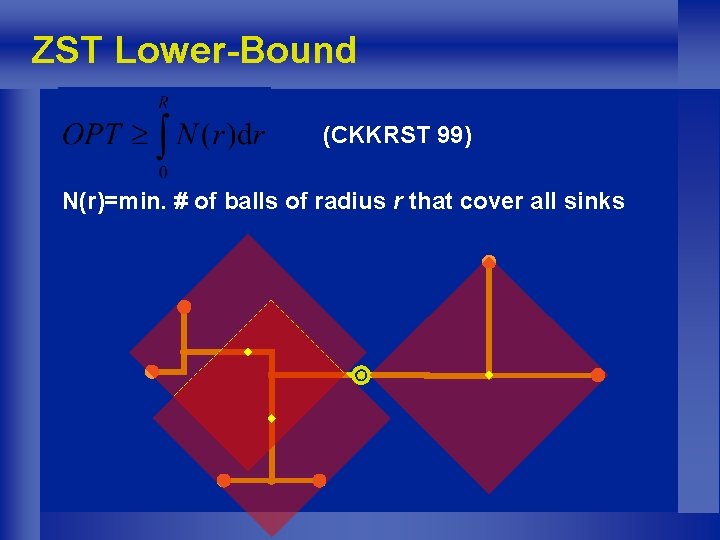
ZST Lower-Bound (CKKRST 99) N(r)=min. # of balls of radius r that cover all sinks

ZST Lower-Bound (CKKRST 99) N(r)=min. # of balls of radius r that cover all sinks

ZST Lower-Bound (CKKRST 99) N(r)=min. # of balls of radius r that cover all sinks

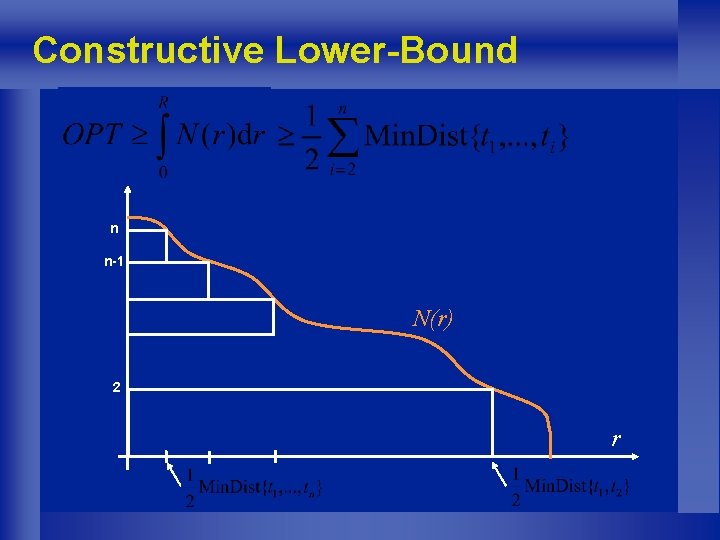
Constructive Lower-Bound Computing N(r) is NP-hard, but … Lemma: For any ordering then of the terminals, if

Constructive Lower-Bound n n-1 N(r) 2 r

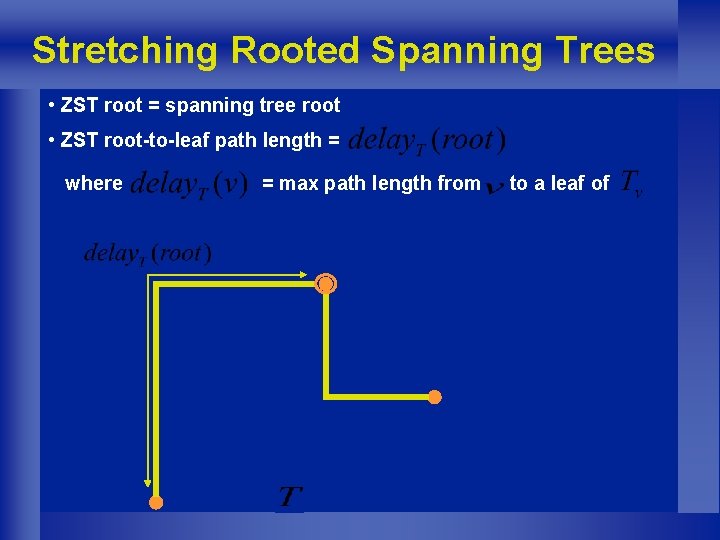
Stretching Rooted Spanning Trees • ZST root = spanning tree root • ZST root-to-leaf path length = where = max path length from to a leaf of

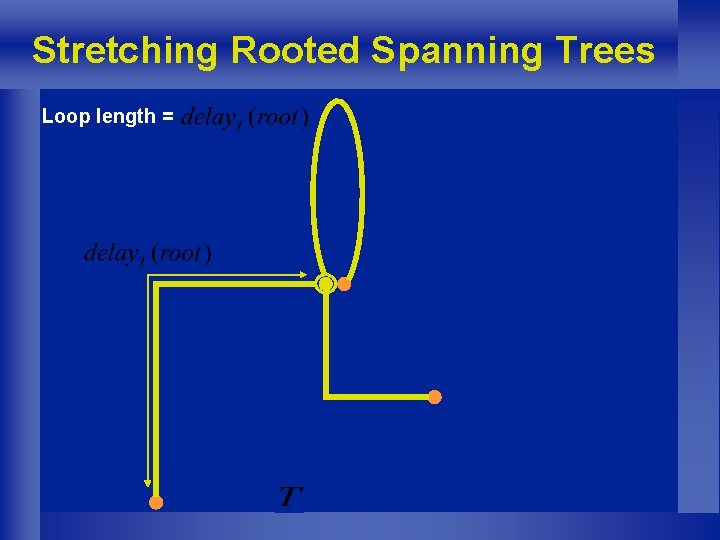
Stretching Rooted Spanning Trees Loop length =

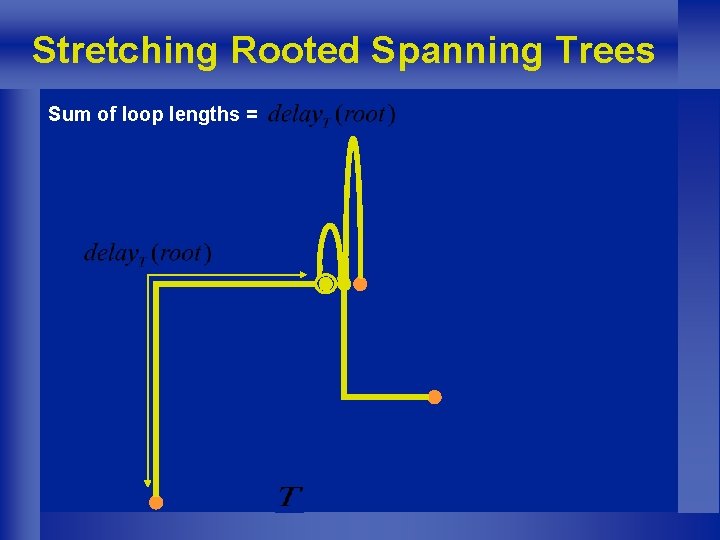
Stretching Rooted Spanning Trees Sum of loop lengths =

Zero-Skew Spanning Tree Problem Theorem: Every rooted spanning tree stretched to a ZST of total length can be where Zero-Skew Spanning Tree Problem: Find rooted spanning tree minimizing

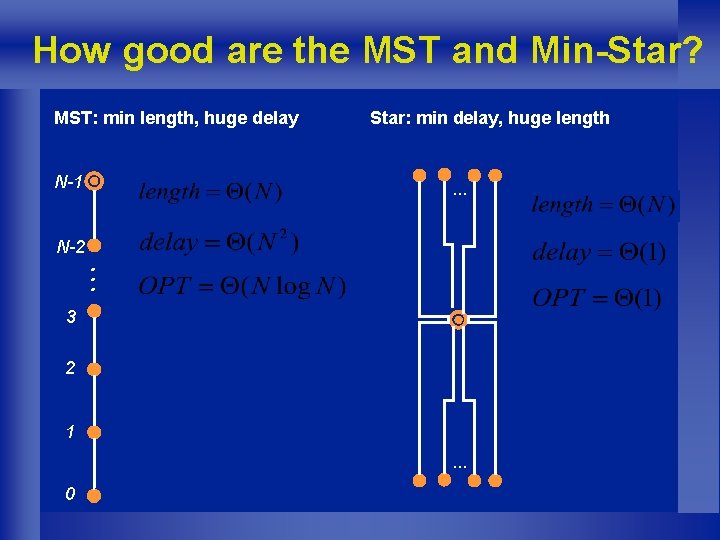
How good are the MST and Min-Star? MST: min length, huge delay N-1 N-2 Star: min delay, huge length … . . . 3 2 1 … 0

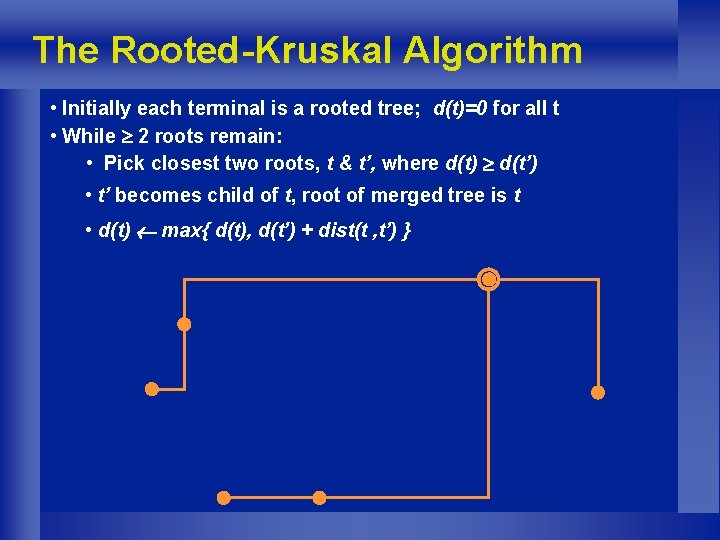
The Rooted-Kruskal Algorithm • Initially each terminal is a rooted tree; d(t)=0 for all t • While 2 roots remain: • Pick closest two roots, t & t’, where d(t) d(t’) • t’ becomes child of t, root of merged tree is t • d(t) max{ d(t), d(t’) + dist(t , t’) } t’ t

The Rooted-Kruskal Algorithm • Initially each terminal is a rooted tree; d(t)=0 for all t • While 2 roots remain: • Pick closest two roots, t & t’, where d(t) d(t’) • t’ becomes child of t, root of merged tree is t • d(t) max{ d(t), d(t’) + dist(t , t’) }

How good is Rooted-Kruskal? • Initially each terminal is a rooted tree; d(t)=0 for all t • While 2 roots remain: • Pick closest two roots, t & t’, where d(t) d(t’) • t’ becomes child of t, root of merged tree is t • d(t) max{ d(t), d(t’) + dist(t , t’) } Lemma: delay(T) length(T) At the end of the algorithm, d(t)=delay (t ) T When edge (t , t’) is added to T: • length(T) increases by dist(t , t’) • delay(T) increases by at most dist(t , t’)

How good is Rooted-Kruskal? • Initially each terminal is a rooted tree; d(t)=0 for all t • While 2 roots remain: • Pick closest two roots, t & t’, where d(t) d(t’) • t’ becomes child of t, root of merged tree is t • d(t) max{ d(t), d(t’) + dist(t , t’) } Lemma: length(T) 2 OPT Number terminals in reverse order of becoming non-roots length(T) =

Factor 4 Approximation Algorithm: Rooted-Kruskal + Stretching • Length after stretching = length(T) + delay(T) • delay(T) length(T) • length(T) 2 OPT ZST length 4 OPT

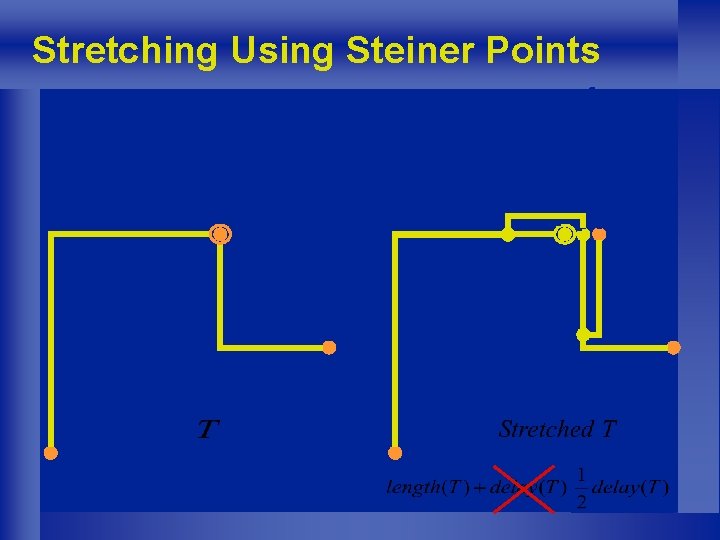
Stretching Using Steiner Points

Factor 3 Approximation Algorithm: Rooted-Kruskal + Improved Stretching • Length after stretching = length(T) + ½ delay(T) • delay(T) length(T) • length(T) 2 OPT ZST length 3 OPT

Practical Considerations • For a fixed topology, minimum length ZST can be found in linear time using the Deferred Merge Embedding (DME) algorithm [Eda 91, BK 92, CHH 92] • Practical algo: Rooted-Kruskal + Stretching + DME Theorem: Both stretching algorithms lead to the same ZST topology when applied to the Rooted. Kruskal tree

Running Time • Stretching: O(N log. N) • Rooted-Kruskal: O(N log. N) using the dynamic closest-pair data structure of [B 98] • DME: O(N) [Eda 91, BK 92, CHH 92] O(N log. N) overall

Extension to Other Metric Spaces Everything works as in rectilinear plane, except: • Running time of Rooted-Kruskal becomes O(N 2) • No equivalent of DME known for other spaces • The space must be metrically convex to apply second stretching algorithm

Bounded-Skew Trees b-bounded-skew tree: difference between length of any two root-to-leaf paths is at most b Bounded-Skew Tree Problem: given a set of terminals and bound b>0, find a b-bounded-skew tree with minimum total length Previous approximation guarantees [CKKRST 99]: • factor 16. 11 for arbitrary metrics • factor 12. 53 for rectilinear plane Our results: factor 14, resp. 9 approximation

BST construction idea + lower bound Two stage BST construction: • Cover terminals by disjoint b-bounded-skew trees • Connect roots via a zero-skew tree Lemma: For any set of terminals, and any

Constructing the tree cover • T MST on terminals, rooted arbitrarily • While T do: • Find leaf of T furthest from the root • Find its highest ancestor u that still has delay b • Add u to W • Add T u to the tree cover and delete it from T Lemma:

BST Approximation Algorithm: Output tree cover approximate ZST on W

BST Approximation Theorem: Rectilinear Plane: Arbitrary metric spaces:

Summary of Results Problem Metric Zero-Skew General Previous 5. 44 factor New factor Rectilinear 4 3 Bounded-skew General Rectilinear 16. 11 12. 53 14 9

Open Problems • Complexity of ZST problem in rectilinear plane • Complexity of finding the spanning tree with minimum length+delay? • Zero-skew Steiner ratio: supremum, over all sets of terminals, of the ratio between minimum ZST length and minimum spanning tree length+delay • What is the ratio for rectilinear plane? • What is the ratio for arbitrary spaces? ( 4, 3) • Planar ZST / BST