Zarzdzanie projektami Metoda CPM MCX Minimum Cost Expenditure

Zarządzanie projektami Metoda CPM MCX (Minimum Cost Expenditure)

Metoda CPM MCX Metoda CPM stosowana jest w analizie czasowej sieci czynności i służy do minimalizacji czasu realizacji projektu Nie mniej ważnym zagadnieniem jest jednak aspekt ekonomiczny zarządzania projektami i możliwość modyfikacji modelu poprzez kompresję sieci czynności oraz skrócenie czasu wykonywania projektu kosztem dodatkowych zasobów. 2

Metoda CPM MCX W przypadkach wielu praktycznych projektów czas trwania niektórych czynności można skrócić, zwiększając jednak koszt ich realizacji przez przydział dodatkowych zasobów. Klasycznym, znanym z literatury modelem opisującym tę zależność jest model Time/Cost Trade off. 3

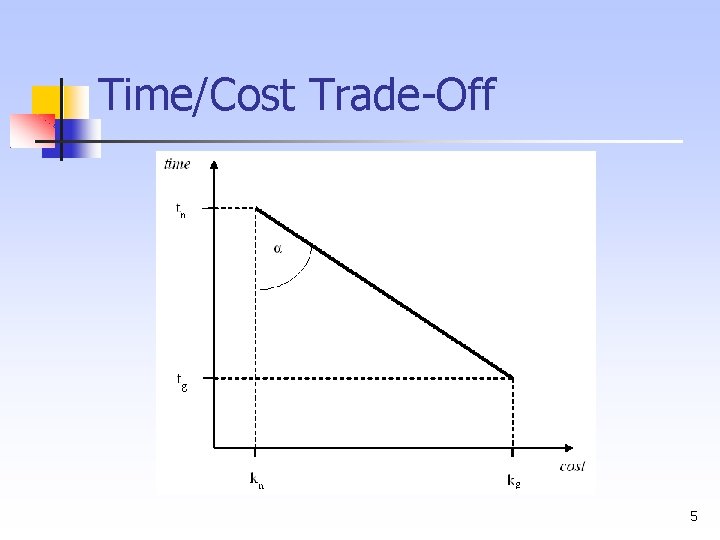
Time/Cost Trade Off W modelu Time/Cost Trade off czas wykonywania czynności jest funkcją kosztu wykonania tej czynności. Funkcja jest nierosnąca i w klasycznym przypadku zakłada się, że jest liniowa, choć w ogólności być tak nie musi. 4

Time/Cost Trade Off 5

Time/Cost Trade Off 6

Metoda CPM MCX stosowana jest w analizie czasowo kosztowej sieci i służy do określenia najkrótszego czasu wykonania projektu tak, aby sumaryczny koszt związany z jego skróceniem był minimalny. Skrócenie czasu wykonania projektu jest możliwe przez skrócenie czynności krytycznych, a największe przyspieszenie powinno przypadać na te czynności krytyczne których koszty przyspieszenia są najmniejsze. 7

Metoda CPM MCX Czynności mają określone kombinacje czasów trwania i kosztów ich realizacji. Zależność czasu trwania czynności od kosztu jej realizacji jest nierosnącą funkcją liniową. Przyjmujemy: tijn normalny czas trwania czynności (i, j) kijn normalny koszt wykonania czynności (i, j) tzn. koszt jej wykonania w czasie tijn tijg graniczny czas wykonania czynności (i, j) tzn. najkrótszy ze względów technicznych i technologicznych czas wykonania tej czynności przy użyciu wszystkich dostępnych zasobów 8

Metoda CPM MCX kijg – koszt graniczny wykonania czynności (i, j) czyli koszt wykonania w czasie granicznym sij – średni gradient kosztów czyli współczynnik wzrostu kosztów na jednostkę czasu (koszt skrócenia czynności (i, j) o 1 jednostkę): Dla czynności, których skrócenie jest niemożliwe, czyli tijg= tijn średni gradient kosztów nie istnieje (nie jest równy zero!) 9

Algorytm kompresji sieci 1. Przeprowadzić analizę czasową sieci dla normalnych czasów wykonania czynności i wyznaczyć ścieżkę krytyczną. 2. Obliczyć średnie gradienty kosztów wszystkich czynności krytycznych i wyeliminować czynności krytyczne dla których gradient kosztów nie istnieje. 3. Rozpocząć proces kompresji sieci zaczynając skracanie od tej czynności krytycznej, dla której średni gradient kosztów jest najmniejszy. 10

Algorytm kompresji sieci 4. Wybraną czynność skrócić o możliwie największą liczbę jednostek, uwzględniając jednak 2 ograniczenia: 1. czas graniczny danej czynności 2. minimalny zapas całkowity którejkolwiek czynności niekrytycznej Z p. 2 może się wiązać pojawienie się nowej ścieżki krytycznej. 5. Przy istnieniu dwóch lub więcej ścieżek krytycznych należy skracać czynności o tą samą wartość na wszystkich równoległych ścieżkach krytycznych. 11

Algorytm kompresji sieci 6. Najkrótszy czas realizacji projektu osiąga się, gdy wszystkie czynności leżące na którejkolwiek ścieżce krytycznej osiągną swe czasy graniczne. 7. Koszty przyspieszenia na każdym etapie oblicza się jako iloczyn średniego gradientu kosztów dla danej czynności i liczby jednostek czasu, o którą dana czynność została skrócona. 8. Łączny koszt przyspieszenia jest sumą kosztów na poszczególnych etapach. 12

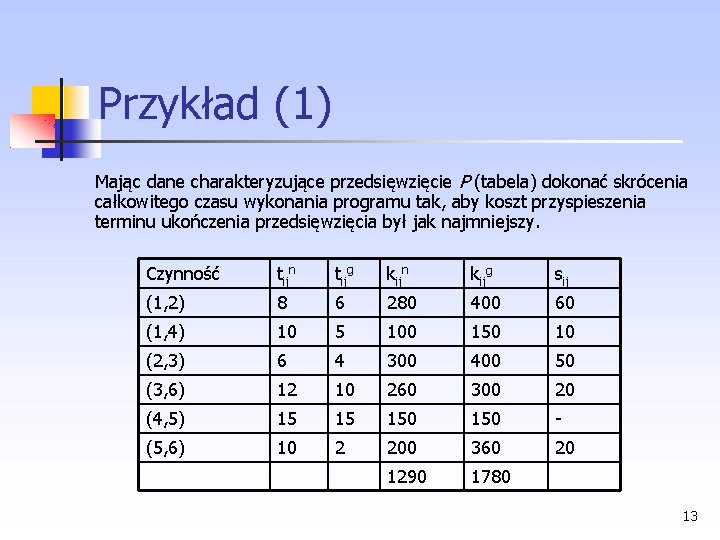
Przykład (1) Mając dane charakteryzujące przedsięwzięcie P (tabela) dokonać skrócenia całkowitego czasu wykonania programu tak, aby koszt przyspieszenia terminu ukończenia przedsięwzięcia był jak najmniejszy. Czynność tijn tijg kijn kijg sij (1, 2) 8 6 280 400 60 (1, 4) 10 5 100 150 10 (2, 3) 6 4 300 400 50 (3, 6) 12 10 260 300 20 (4, 5) 15 15 150 (5, 6) 10 2 200 360 20 1290 1780 13

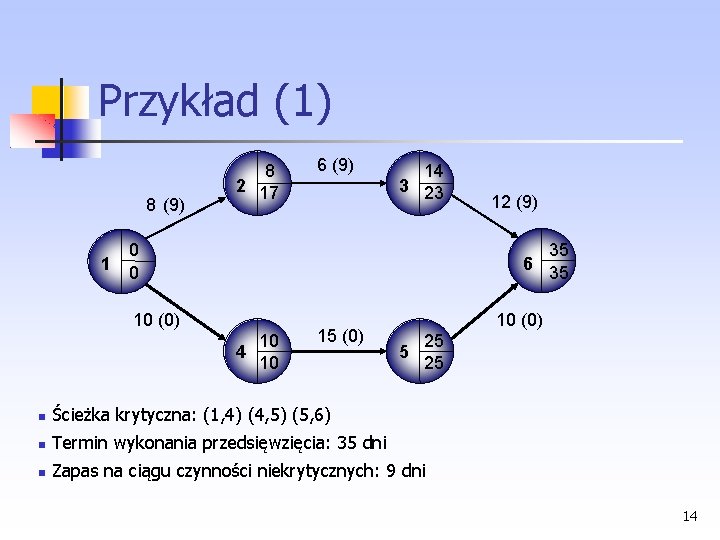
Przykład (1) 8 (9) 1 8 2 17 6 (9) 14 3 23 0 0 12 (9) 35 6 35 10 (0) 10 4 10 15 (0) 10 (0) 5 25 25 Ścieżka krytyczna: (1, 4) (4, 5) (5, 6) Termin wykonania przedsięwzięcia: 35 dni Zapas na ciągu czynności niekrytycznych: 9 dni 14

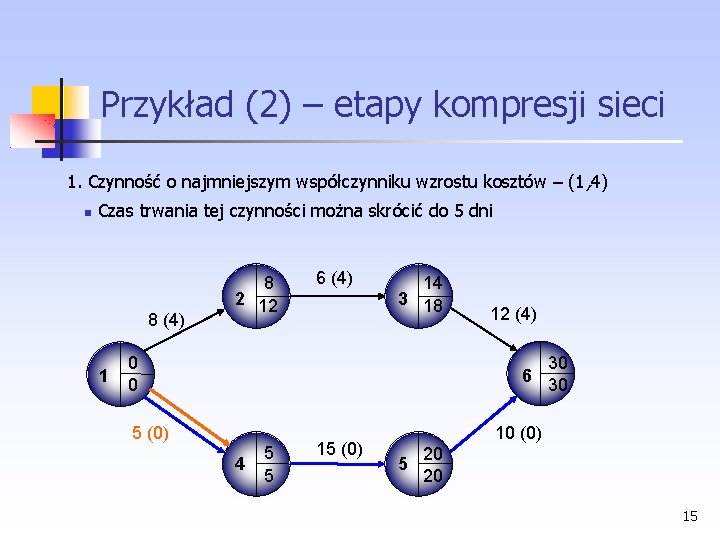
Przykład (2) – etapy kompresji sieci 1. Czynność o najmniejszym współczynniku wzrostu kosztów – (1 , 4) Czas trwania tej czynności można skrócić do 5 dni 8 (4) 1 8 2 12 6 (4) 14 3 18 0 0 12 (4) 30 6 30 5 (0) 4 5 5 15 (0) 10 (0) 5 20 20 15

Przykład (3) Czas realizacji przedsięwzięcia zostaje skrócony do 30 dni Koszty: 16

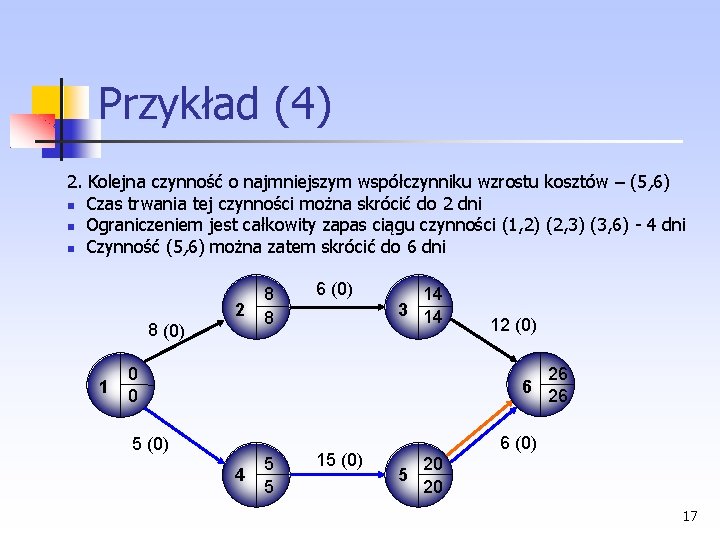
Przykład (4) 2. Kolejna czynność o najmniejszym współczynniku wzrostu kosztów – (5 , 6) Czas trwania tej czynności można skrócić do 2 dni Ograniczeniem jest całkowity zapas ciągu czynności (1, 2) (2, 3) (3, 6) 4 dni Czynność (5, 6) można zatem skrócić do 6 dni 2 8 (0) 1 8 8 6 (0) 14 3 14 0 0 12 (0) 26 6 26 5 (0) 4 5 5 15 (0) 6 (0) 5 20 20 17

Przykład (5) Czas realizacji przedsięwzięcia skrócony zostaje do 26 dni Koszty: Ścieżki krytyczne: (1, 2) (2, 3) (3, 6) i (1, 4) (4, 5) (5, 6) Dalsza kompresja sieci jest możliwa 18

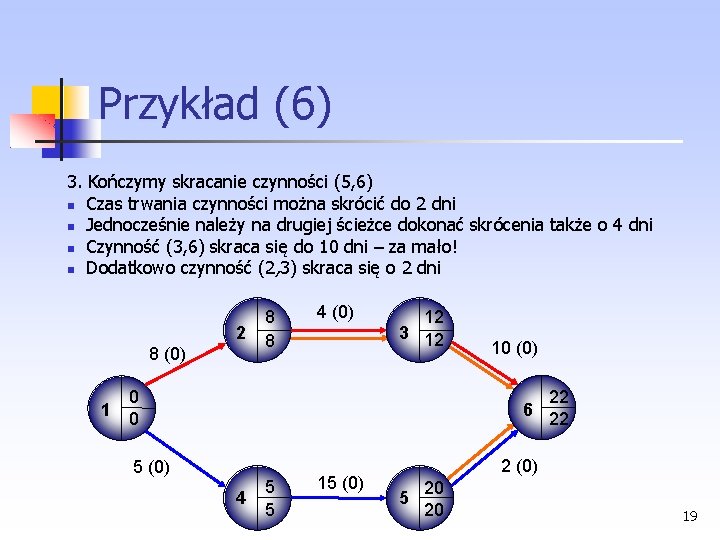
Przykład (6) 3. Kończymy skracanie czynności (5, 6) Czas trwania czynności można skrócić do 2 dni Jednocześnie należy na drugiej ścieżce dokonać skrócenia także o 4 dni Czynność (3, 6) skraca się do 10 dni – za mało! Dodatkowo czynność (2, 3) skraca się o 2 dni 2 8 (0) 1 8 8 4 (0) 12 3 12 0 0 10 (0) 22 6 22 5 (0) 4 5 5 15 (0) 2 (0) 5 20 20 19

Przykład (7) Czas realizacji przedsięwzięcia skraca się do 22 dni Osiagnieto bilans na obu ścieżkach Koszty związane z tymi czynnościami są następujące: dla (5, 6): dla (3, 6): dla (2, 3): K 3 = 80 + 40 + 100 = 220 20

Przykład (8) podsumowanie Dalsze skracanie jest niemożliwe, gdyż wszystkie czynności leżące na ścieżce krytycznej (1, 4) (4, 5) (5, 6) osiągnęły czasy graniczne Czas trwania przedsięwzięcia – 22 dni Koszt związany ze skróceniem czasu wykonania przedsięwzięcia: 21

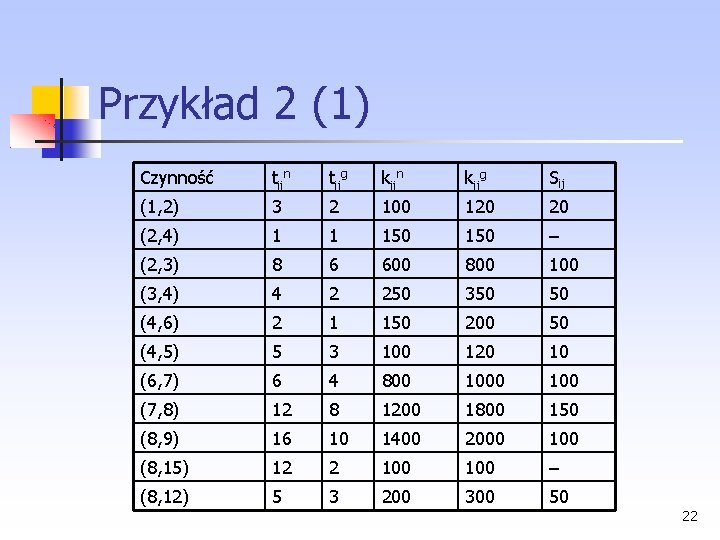
Przykład 2 (1) Czynność tijn tijg kijn kijg Sij (1, 2) 3 2 100 120 20 (2, 4) 1 1 150 – (2, 3) 8 6 600 800 100 (3, 4) 4 2 250 350 50 (4, 6) 2 1 150 200 50 (4, 5) 5 3 100 120 10 (6, 7) 6 4 800 100 (7, 8) 12 8 1200 1800 150 (8, 9) 16 10 1400 2000 100 (8, 15) 12 2 100 – (8, 12) 5 3 200 300 50 22

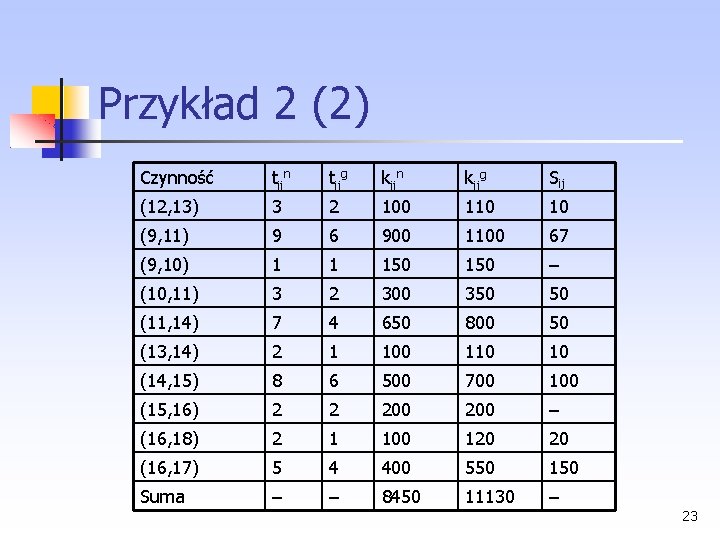
Przykład 2 (2) Czynność tijn tijg kijn kijg Sij (12, 13) 3 2 100 110 10 (9, 11) 9 6 900 1100 67 (9, 10) 1 1 150 – (10, 11) 3 2 300 350 50 (11, 14) 7 4 650 800 50 (13, 14) 2 1 100 110 10 (14, 15) 8 6 500 700 100 (15, 16) 2 2 200 – (16, 18) 2 1 100 120 20 (16, 17) 5 4 400 550 150 Suma – – 8450 11130 – 23

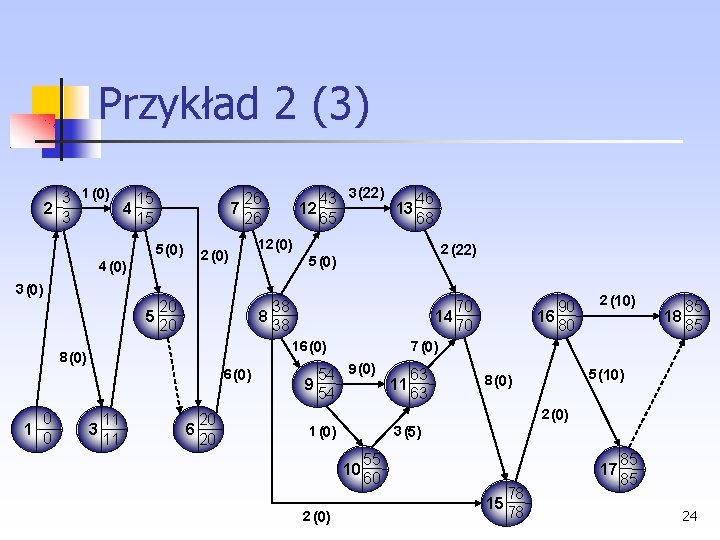
Przykład 2 (3) 3 1 (0) 15 2 4 3 15 5 (0) 4 (0) 3 (0) 20 5 20 12 (0) 2 (22) 5 (0) 38 8 38 70 14 70 16 (0) 8 (0) 6 (0) 0 1 0 43 3 (22) 46 12 13 65 68 26 7 26 11 3 11 20 6 20 90 16 80 2 (10) 18 85 85 7 (0) 54 9 (0) 63 9 11 54 63 5 (10) 8 (0) 2 (0) 1 (0) 3 (5) 10 2 (0) 55 60 17 15 78 78 85 85 24

Przykład 2 (4) Ścieżka krytyczna obejmuje następujące czynności: (1, 2), (2, 3), (3, 4), (4, 5), (5, 6), (6, 7), (7, 8), (8, 9), (9, 11), (11, 14), (14, 15), (15, 16), (16, 17), (17, 18) Minimalny zapas czasu w ciągu czynności niekrytycznych wynosi 5 tygodni (o tyle można w początkowym etapie skracać czas realizacji czynności leżących na ścieżce krytycznej) Skracanie czasu należy rozpocząć od czynności (4, 5), gdyż dla niej średni gradient kosztów S jest najmniejszy i wynosi 10 Czas trwania czynności (4, 5) można skrócić z 5 do 3 tygodni (tijg = 3) 25

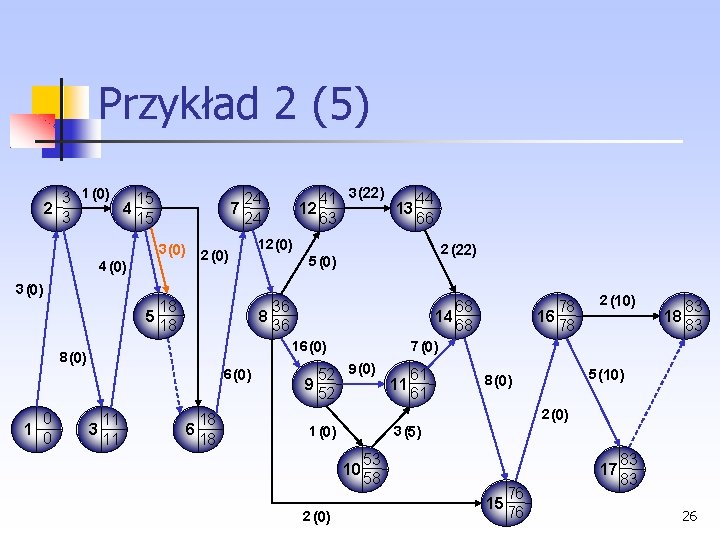
Przykład 2 (5) 3 1 (0) 15 2 4 3 15 3 (0) 4 (0) 3 (0) 2 (0) 18 5 18 12 (0) 2 (22) 5 (0) 36 8 36 68 14 68 16 (0) 8 (0) 6 (0) 0 1 0 41 3 (22) 44 12 13 63 66 24 7 24 11 3 11 18 6 18 78 16 78 2 (10) 18 83 83 7 (0) 52 9 (0) 61 9 11 52 61 5 (10) 8 (0) 2 (0) 1 (0) 3 (5) 10 2 (0) 53 58 17 15 76 76 83 83 26

Przykład 2 (6) Czas realizacji przedsięwzięcia skraca się do 83 tygodni Wzrost kosztów: 27

Przykład 2 (7) Następną czynnością ze ścieżki krytycznej o najmniejszym średnim gradiencie kosztów jest czynność (1, 2), której czas trwania można skrócić o tydzień Wzrost kosztów: 28

Przykład 2 (8) 2 1 (0) 14 2 14 3 (0) 4 (0) 2 (0) 17 5 17 12 (0) 2 (22) 5 (0) 35 8 35 67 14 67 16 (0) 8 (0) 6 (0) 0 1 0 40 3 (22) 43 12 13 62 65 23 7 23 10 17 6 17 77 16 77 2 (10) 18 82 82 7 (0) 51 9 (0) 60 9 11 51 60 5 (10) 8 (0) 2 (0) 1 (0) 3 (5) 10 2 (0) 52 57 17 15 75 75 82 82 29

Przykład 2 (9) W tym momencie dwie czynności wykazują najniższy średni gradient kosztu S = 50: (3, 4) i (11, 14). Należy więc skracać czasy trwania tych czynności odpowiednio o 2 i 3 tygodnie, co kosztuje: 30

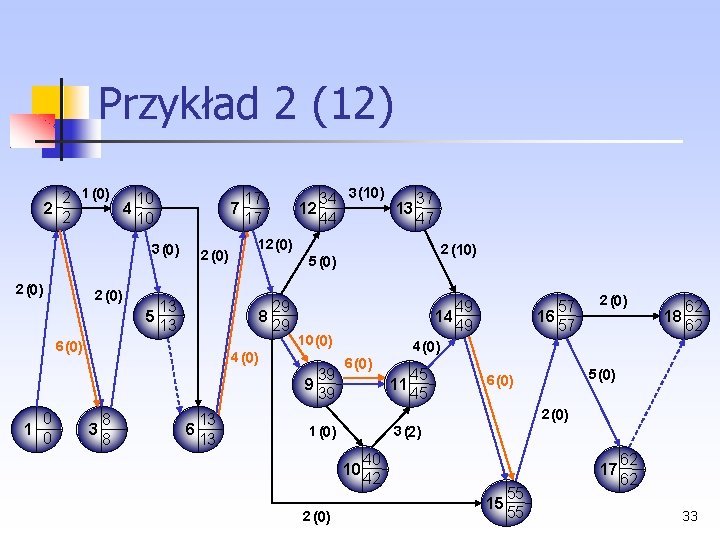
Przykład 2 (10) 2 1 (0) 12 2 4 2 12 3 (0) 2 (0) 15 5 15 12 (0) 2 (19) 5 (0) 33 8 33 4 (0) 16 (0) 8 (0) 6 (0) 0 1 0 38 3 (19) 41 12 13 57 60 21 7 21 10 3 10 15 6 15 49 9 (0) 58 9 11 49 58 62 14 62 72 16 72 2 (0) 18 77 77 5 (0) 8 (0) 2 (0) 1 (0) 3 (5) 10 2 (0) 50 55 17 15 70 70 77 77 31

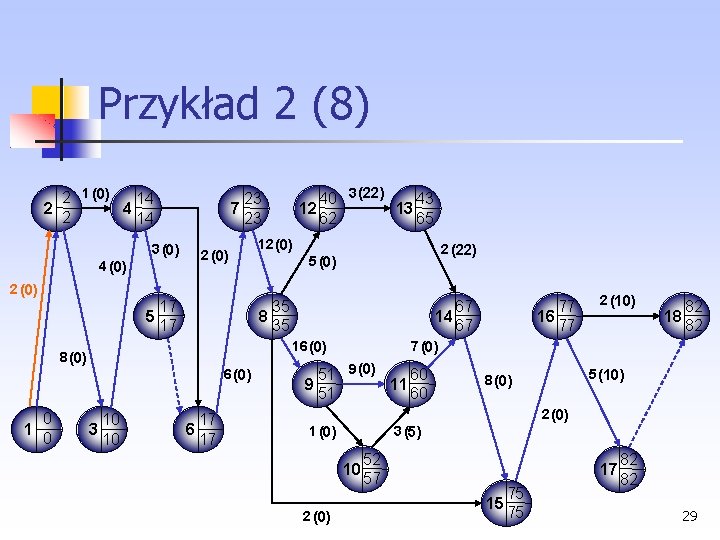
Przykład 2 (11) Na ścieżce krytycznej nadal znajdują się czynności, których czas trwania można skrócić. Nie pojawiła się także nowa ścieżka krytyczna. Należy skracać kolejno czynności: (9, 11), dla której S = 67 oraz równolegle czynności, dla których S = 100 (2, 3) (6, 7) (8, 9) (14, 15) Koszt jest następujący: 32

Przykład 2 (12) 2 1 (0) 10 2 4 2 10 3 (0) 2 (0) 17 7 17 2 (0) 0 12 (0) 29 8 29 4 (0) 8 3 8 13 6 13 2 (10) 5 (0) 13 5 13 6 (0) 34 3 (10) 37 12 13 44 47 49 14 49 10 (0) 39 9 39 57 16 57 2 (0) 18 62 62 4 (0) 6 (0) 11 45 45 5 (0) 6 (0) 2 (0) 1 (0) 3 (2) 10 2 (0) 40 42 17 15 55 55 62 62 33

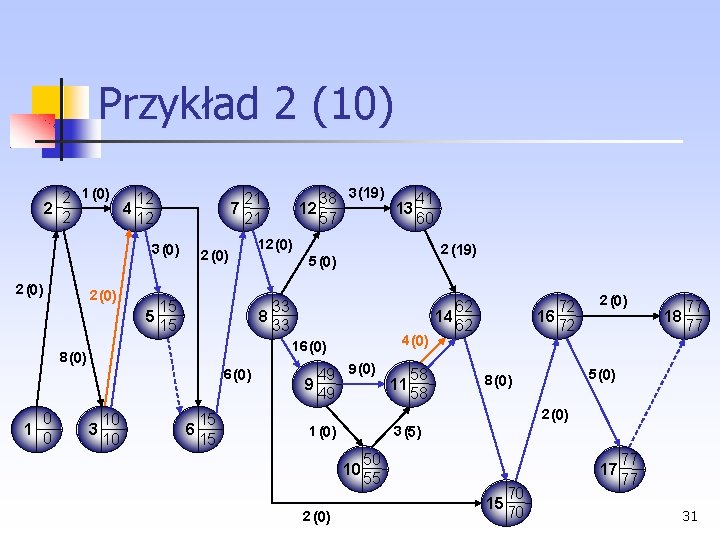
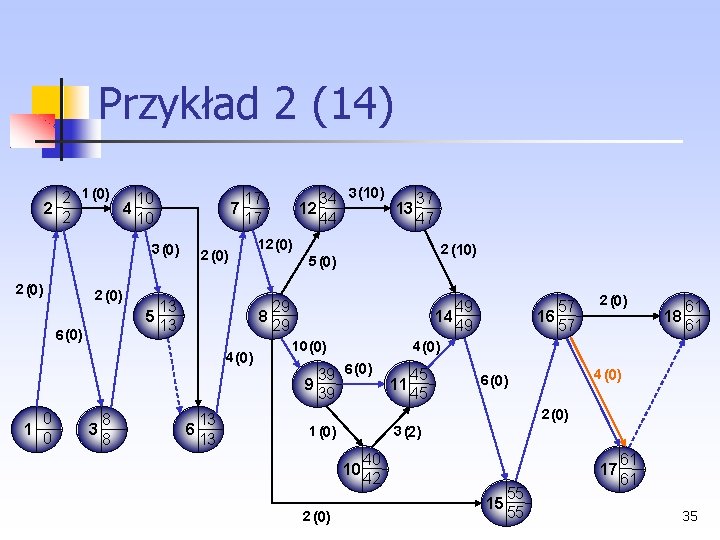
Przykład 2 (13) Dalszych oszczędności czasowych można dokonywać, skracając czynności ze ścieżki krytycznej (16, 17), S = 150. Koszt jest następujący: 34

Przykład 2 (14) 2 1 (0) 10 2 4 2 10 3 (0) 2 (0) 6 (0) 2 (0) 13 5 13 8 12 (0) 2 (10) 5 (0) 29 8 29 4 (0) 0 1 0 34 3 (10) 37 12 13 44 47 17 13 6 13 49 14 49 10 (0) 57 16 57 2 (0) 18 61 61 4 (0) 39 6 (0) 9 39 11 45 45 4 (0) 6 (0) 2 (0) 1 (0) 3 (2) 10 2 (0) 40 42 17 15 55 55 61 61 35

Przykład 2 (15) W tym momencie skracanie czasu realizacji projektu nie jest już możliwe, gdyż wszystkie czynności leżące na ścieżce krytycznej osiągnęły czasy graniczne. Nie pojawiła się także nowa ścieżka krytyczna. Czas opracowania nowego produktu udało się skrócić z 85 tygodni do 61 tygodni. Koszt tego przyspieszenia wyniósł: Kp=(K 1+K 2+…+K 10)=20+20+100+150+201+200+400+200+150=1641 36

Przykład 2 (16) podsumowanie Całkowity koszt realizacji przedsięwzięcia w skróconym czasie wynosi więc 10 091 jednostek pieniężnych. Należy zauważyć, że w każdym momencie można zrezygnować z dalszego skracania czasu realizacji projektu, gdy koszty wprowa dzenia produktu na rynek w szybszym tempie przekroczą akceptowalny poziom. 37

Przykład 2 (17) podsumowanie Skracanie czasu trwania czynności nie dotyczyło wszystkich czynności leżących na ścieżce krytycznej, gdyż dla niektórych z nich nie istniał gradient kosztu, co oznacza, że nie było technicznych lub technologicznych możliwości skrócenia czasu ich trwania. W przypadku pojawienia się równoległej ścieżki krytycznej należałoby dokonywać skracania czasu trwania poszczególnych czynności równolegle na obydwu ścieżkach. W tym przypadku o kolejności skracania czasu także decydowałby średni gradient kosztu. 38

Podsumowanie Analiza kosztowo czasowa CPM MCX jest niewątpliwie użytecznym uzupełnieniem techniki CPM. Należy pamiętać, że nie zawsze zależności między kosztem przyspieszenia danej czynności a czasem tego przyspieszenia mają charakter liniowy. Istnieje ryzyko przeszacowania kosztów, co może doprowadzić do nieprecyzyjnych obliczeń i pojawienia się dodatkowych, niespodziewanych kosztów realizacji projektu. 39