ZAKON OUVANJA KOLIINE POLJA zakon ouvanja mase U

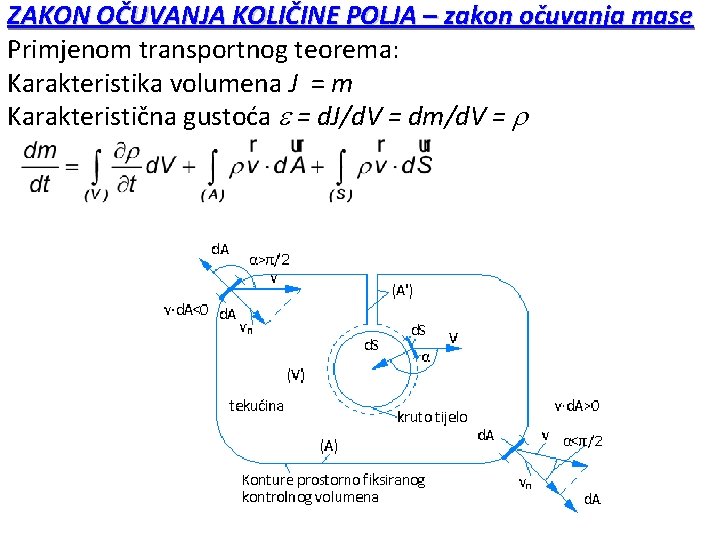
ZAKON OČUVANJA KOLIČINE POLJA – zakon očuvanja mase U vremenskom trenutku t u materijalnom volumenu V(t) nalazi se određena količina tekućine izražena masom m. Uvjet kontinuiteta: u volumenu V(t) nema “praznog” prostora. Zakon očuvanja mase: u materijalnom volumenu tekućine ograničenom sa oplošjem A(t) tekućina ne može nestajati ni nastajati Integralna formulacija zakona očuvanja mase odnosno jednadžba kontinuiteta Gustoća u unutrašnjosti kontrolnog volumena = (t, r) može biti promjenljiva u vremenu i u prostoru. Prelaskom sa materijalnog volumena na kontrolni volumen, pripadna kontrolna površina može se podijeliti na “slobodni” dio A i dio na kontaktu s krutim tijelom S.

ZAKON OČUVANJA KOLIČINE POLJA – zakon očuvanja mase Primjenom transportnog teorema: Karakteristika volumena J = m Karakteristična gustoća = d. J/d. V = dm/d. V =

ZAKON OČUVANJA KOLIČINE POLJA – zakon očuvanja mase Ukupna promjena mase u vremenu sastoji se od lokalne promjene (prvi član sa lijeve strane) i različit je od 0 u slučaju nestacionarnog tečenja. Preostali dio desne strane su konvektivni članovi koji predstavljaju tok (eng: flux) mase kroz odabrane kontrolne površine A i S a ovisan o brzini okomitoj na površinu vn i veličini …… i. Samo normalna komponenta brzine vn pronosi neku količinu tekućine, dok tangencijalna komponenta brzine vt utječe samo na deformaciju djelića tekućine unutar kontrolnog volumena.

ZAKON OČUVANJA KOLIČINE POLJA – zakon očuvanja mase Ukoliko je vektor brzina istog smjera kao i vanjska normala kontrolne površine i onda su i pozitivni. Vektor vanjske normale kontrolne površine smjeru krutog tijela. uvijek gleda u Kroz površinu A' proticati će jednaka količina tekućine u smislu izlaza iz i ulaza u kontrolni volumen kroz nju.

ZAKON OČUVANJA KOLIČINE POLJA – zakon očuvanja mase Upotrebom GGO teorema: iz izraza: dobiva se: Primjenom prve leme variacionog računa (vrijednost integrala = 0 samo ukoliko je podintegralna funkcija = 0) dobiva se diferencijalna forma jednadžbe kontinuiteta: Vrijedi za stišljive i nestišljive tekućine.

ZAKON OČUVANJA KOLIČINE POLJA – zakon očuvanja mase Ukoliko je stacionarno tečenje: lokalna promjena / t = 0. Ukoliko je tekućina homogene: grad = 0. Budući da je 0, slijedi = 0. Zaključno, za slučaj trodimenzionalnog stacionarnog tečenja nestišljive tekućine: Za slučaj nestacionarnog tečenja stišljive tekućine pri brzinama manjim od brzine zvuka (vodni udar):

KINETIKA (DINAMIKA) - ZOKG Analizira se gibanje tekućine pod djelovanjem sila i naprezanja. Izvodi se opća jednadžba kojom se povezuje ubrzanje, masene sile i djelujuća naprezanja za diferencijalni element tekućine. Tekućina se promatra kao kontinuum. Uvođenjem konstitutivnih jednadžbi za odnos između brzine deformacija i stanja naprezanja dobivaju se Navier-Stokesove jednadžbe. Temelj izvoda je II Newtonov aksiom: Promatra se “bilanca” vanjskih sila na djelić tekućine.

KINETIKA (DINAMIKA) - ZOKG Ukupna promjena (brzina promjene) količine gibanja u vremenu definirana je kao: Masene sile poput gravitacije mogu se kvantificirati gradijentom potencijala (npr. gravitacioni potencijal). Povšinske sile su kontaktne sile koje se mogu razložiti na normalnu i posmičnu komponentu.

KINETIKA (DINAMIKA) - ZOKG Djelovane sila izražava se temeljem površinskih naprezanja. U kartezijevom sustavu pojavljuje se simetrični tenzor naprezanja s 3 člana normalnih naprezanja (dijagonalni članovi) i 6 članova tangencijalnog naprezanja.

KINETIKA (DINAMIKA) - ZOKG U analizi dvodimenzionalnog problema tenzor naprezanja poprima oblik: Razvojem Taylorovog reda s obuhvatom samo prvog člana (za x smjer) dobiva se jednakost:

KINETIKA (DINAMIKA) - ZOKG Uvrštavanjem u II Newtonov aksiom (zakon očuvanja količine gibanja) dobiva se za x smjer: Odnosno u vektorskoj formi za 3 D problem, ili po komponentama,

KINETIKA (DINAMIKA) - ZOKG Problem je sadržan u činjenici da za rješenje 9 nepoznanica (tri komponente brzina i 6 komponenti naprezanja) na raspolaganju imamo samo 4 jednadžbe (3 za količinu gibanja i 1 jednadžba kontinuiteta). Konstitutivne jednadžbe izražavaju naprezanja u funkciji brzina (točnije brzine deformacija). Tenzor naprezanja sadrži dva dijela. Jedan je vezan uz tlak p a drugi uz viskozna naprezanja ( ).

KINETIKA (DINAMIKA) - ZOKG Tlak p predstavlja izotropna normalna naprezanja neovisna o brzini ili viskoznosti. Viskozna naprezanja u Newtonovim tekućinama su linearno proporcionalna brzini deformacije i viskoznosti (odnosno elementima ei, j simetričnog dijela gradijentnog tenzora brzina): Upotrebom dinamičkog koeficijenta viskoznosti za konstantu proporcionalnosti tenzor viskoznih naprezanja u kompaktnoj formi:

KINETIKA (DINAMIKA) - ZOKG Za Newtonove nestišljive tekućine tenzor ukupnog naprezanja definiran je članovima: Primjerice: Uvođenjem konstitutivnih jednadžbi u II Newtonov aksiom (zakon očuvanja količine gibanja) dobiva se tzv. Navier. Stokesova jednadžba:

KINETIKA (DINAMIKA) - ZOKG Zajedno s jednadžbom kontinuiteta dobiven je “zatvoren” sustav pogodan za opis strujanja Newtonove nestišljive tekućine (4 jednadžbe i 4 nepoznanice, 3 komponente brzine i tlak):

DINAMIKA – Reynolds za turbulentno strujanje Turbulentni režim tečenja pojavljuje se u najvećem broju inženjerskih problema. Mjerenje brzina u fiksnoj točki cijevi kružnog proticajnog profila u kojoj se odvija tečenje pod tlakom pokazuje sljedeće rezultate: 1 - statistički stacionarno turbulentno tečenje pri statistički stacionarnom tlaku 2 - statistički nestacionarno turbulentno tečenja pri statistički nestacionarnom tlaku.

DINAMIKA – Reynolds za turbulentno strujanje Stvarna (trenutna) vrijednost brzine ili tlaka prikazuje sa sumom statistički dobivene srednje vrijednosti promatranog polja (brzine, tlaka, temperature) i u vremenu fluktuirajuće komponente promatranog polja: Srednja vrijednost fluktuirajuće komponente promatranog polja u periodu osrednjavanja jednaka je nuli. Duljina perioda osrednjavanja ovisi o pojavi koja se analizira. Navedeni pristup opisu turbulencije je stohastičke prirode budući se strujanje promatra kao stohastički proces sa slučajnom varijablom E. U nastavku se komentiraju samo slučajevi turbulentnog strujanja homogene tekućine.

DINAMIKA – Reynolds za turbulentno strujanje Jednadžba kontinuiteta za turbulentno tečenje homogene nestišljive tekućine ostaje istog oblika bez obzira da li se primjenjuje na trenutnu, osrednjenu ili fluktuirajuću brzinu. Nakon nekoliko koraka algebarske manipulacije i uz zanemarenje članova višeg reda dobiva se Reynolsova jedanadžba: (za x-komponentu)

DINAMIKA – Reynolds za turbulentno strujanje Reynoldsova dinamička jednadžba izvedena je iz Navier-Stokes jednadžbe, zamjenom trenutnih vrijednosti brzine i tlaka s sumom osrednjenih i fluktuirajućih komponenti. Reynoldsove jednadžbe i Navier-Stokesove jednadžbe su slične Na lijevoj strani u Reynoldsovim jednadžbama pojavljuju se novi članovi koji predstavljaju učešće fluktuirajuće komponente u ukupnoj promjeni količine gibanja u vremenu. Premještanjem tih članova na desnu stranu jednadžbe, sa lijeve strane ostaje samo promjena količine osrednjenog gibanja u vremenu.

DINAMIKA – Reynolds za turbulentno strujanje Na desnoj strani sada osim «stvarnih» osrednjenih volumnih sila (npr. gravitacije) i površinskih sila (tlaka i viskoznosti) nalazimo i dodatnu «negativnu virtualnu» silu povezana sa «virtualnim» naprezanjima.

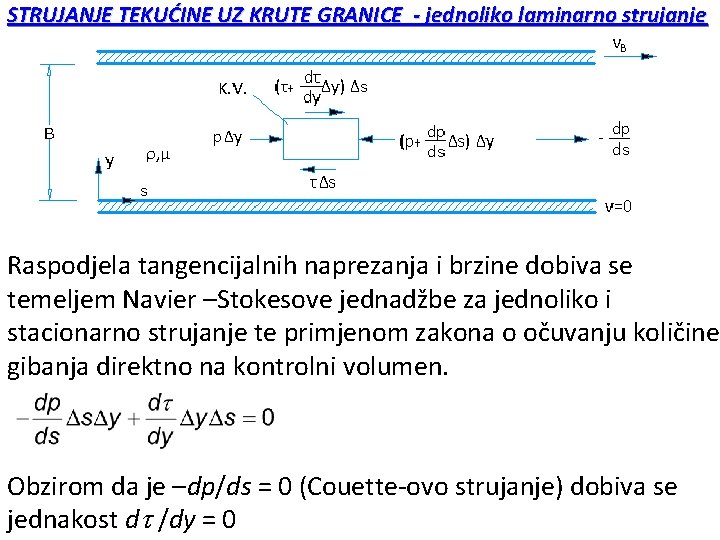
STRUJANJE TEKUĆINE UZ KRUTE GRANICE - jednoliko laminarno strujanje Strujanje realne tekućine oko krutog tijela ili uzduž njegovih krutih granica uzrokuje djelovanje sila na to tijelo. Te sile su otpori strujanju tekućine i dijele se na dvije komponente: Otpori trenja uslijed tangencijalnih naprezanja (djeluju uzduž kontaktne površine tekućine i krutog tijela) Otpor oblika uslijed normalnih naprezanja (djeluju okomito na kontaktne površine) Sada se analiziraju situacije strujanja između dvije međusobno beskonačno široke i paralelne ploče. U prvom slučaju gornja ploča se pomiče konstantnom brzinom VB te nema uzdužnog gradijent tlaka –dp/ds = 0 (Couette strujanje).

STRUJANJE TEKUĆINE UZ KRUTE GRANICE - jednoliko laminarno strujanje Raspodjela tangencijalnih naprezanja i brzine dobiva se temeljem Navier –Stokesove jednadžbe za jednoliko i stacionarno strujanje te primjenom zakona o očuvanju količine gibanja direktno na kontrolni volumen. Obzirom da je –dp/ds = 0 (Couette-ovo strujanje) dobiva se jednakost d /dy = 0

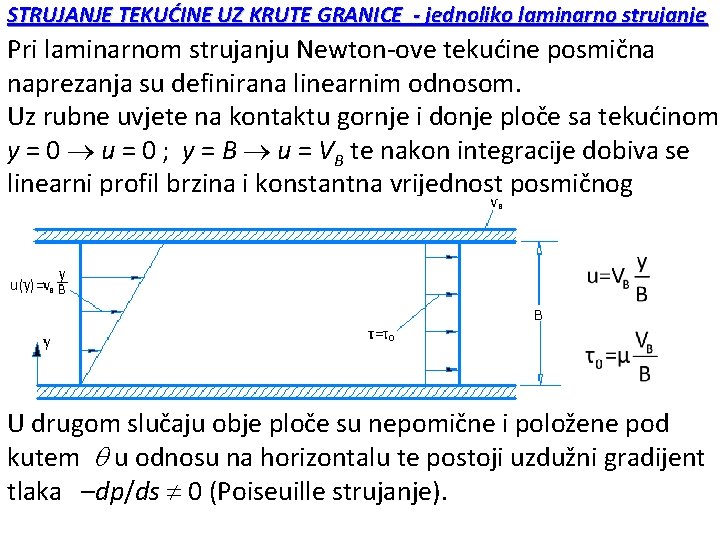
STRUJANJE TEKUĆINE UZ KRUTE GRANICE - jednoliko laminarno strujanje Pri laminarnom strujanju Newton-ove tekućine posmična naprezanja su definirana linearnim odnosom. Uz rubne uvjete na kontaktu gornje i donje ploče sa tekućinom y = 0 u = 0 ; y = B u = VB te nakon integracije dobiva se linearni profil brzina i konstantna vrijednost posmičnog naprezanja: U drugom slučaju obje ploče su nepomične i položene pod kutem u odnosu na horizontalu te postoji uzdužni gradijent tlaka –dp/ds 0 (Poiseuille strujanje).

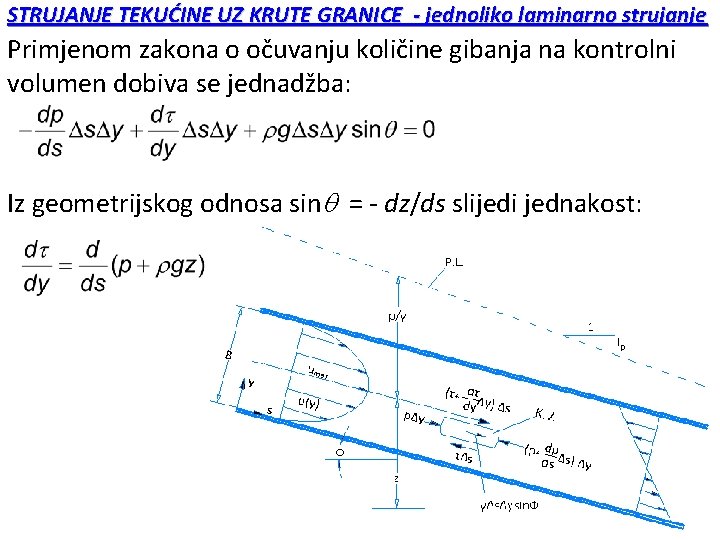
STRUJANJE TEKUĆINE UZ KRUTE GRANICE - jednoliko laminarno strujanje Primjenom zakona o očuvanju količine gibanja na kontrolni volumen dobiva se jednadžba: Iz geometrijskog odnosa sin = - dz/ds slijedi jednakost:

STRUJANJE TEKUĆINE UZ KRUTE GRANICE - jednoliko laminarno strujanje Desna strana jednadžbe predstavlja gradijent piezometarske linije s oznakom GP a upotrebom Newton-ovog zakona = (du/dy): GP = - g. IP = (d 2 u/dy 2) Uz rubne uvjete na kontaktu gornje i donje ploče sa tekućinom y = 0 ; y = B u = 0 te nakon integracije dobiva se parabolični profil brzina i linearna raspodjela posmičnih naprezanja: Maksimalna brzina je u osi (y = B/2) umax = -GPB 2/8 a srednja brzina iznosi V=2/3*umax

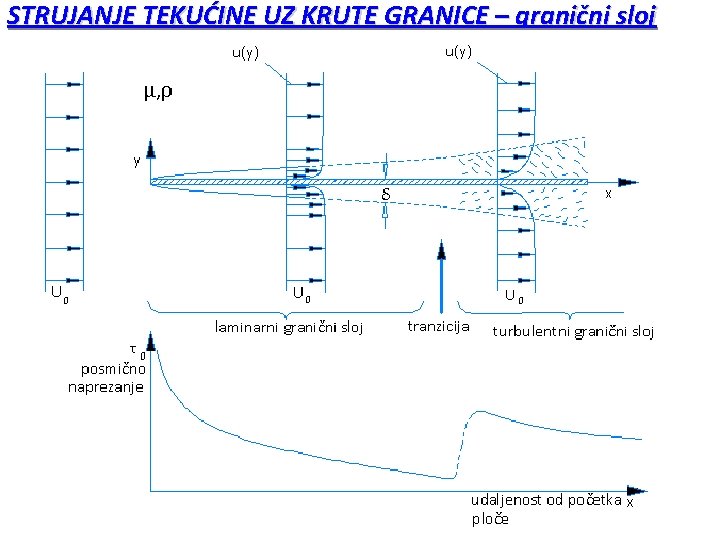
STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj Strujanje u graničnom sloju je nejednoliko i razvija se uzduž smjera strujanja. Granični sloj se nalazi između krute granice i slobodnog toka. Strujanje u graničnom sloju obilježeno je karakteristikama realne-viskozne tekućine dok se područje izvan graničnog sloja (slobodni tok) može shvatiti i kao bezviskozno odnosno strujanje idealne tekućine.

STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj Analizira se slučaj ravne i tanke ploče u mirovanju te tekućine sa brzinom pristrujavanja U 0. Razvija se granični sloj između ploče i područja u kojem je profil brzina još uvijek neporemećen (slobodni tok). U području graničnog sloja brzina strujanja je u funkciji vertikalne udaljenosti od krute ploče u(y). Debljina graničnog sloja se povećava uzduž ploče u( )=0, 99 U 0.

STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj

STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj U graničnom sloju moguća je pojava laminarnog i turbulentnog strujanja. Na početku ploče pojavljuje se laminarni granični sloj a u nastavku strujanja inicira se nestabilnost i turbulencija. Između zone laminarnog i turbulemntnog strujanja pojavljuje se i dionica tranzicije. Za karakterizaciju graničnog sloja definira se i lokalni Reynoldsov broj temeljem udaljenosti od početka ploče Rex = U 0 x /. Gradijent tlaka na području vanjskog toka je dp/dx = 0. Debljina graničnog sloja je vrlo mala tlak u GS je konstantan. Debljina graničnog sloja ovisi o = (x, U 0, , ) odnosno = (t, ). Iz uvjeta dimenzionalne homogenosti:

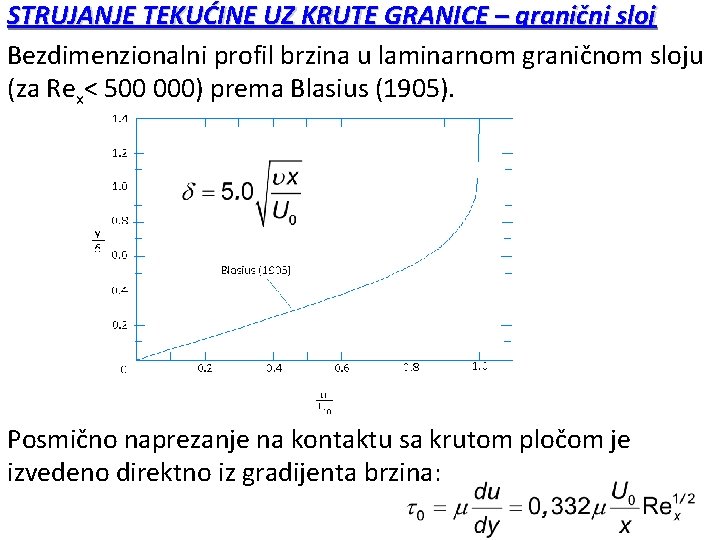
STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj Bezdimenzionalni profil brzina u laminarnom graničnom sloju (za Rex< 500 000) prema Blasius (1905). Posmično naprezanje na kontaktu sa krutom pločom je izvedeno direktno iz gradijenta brzina:

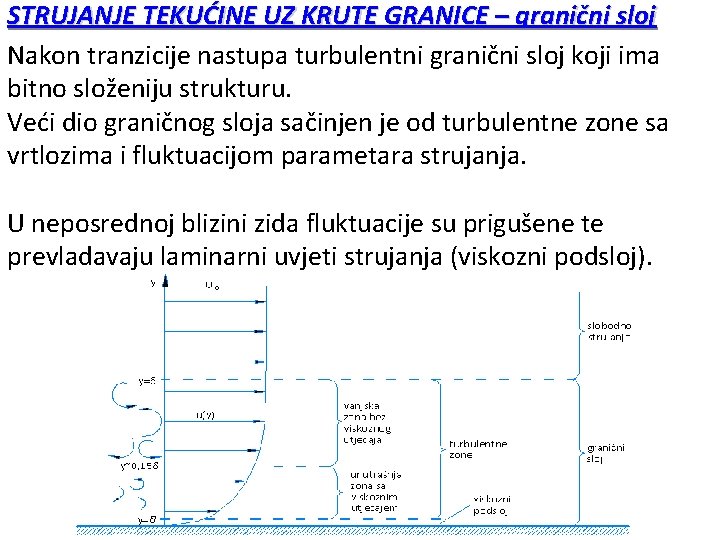
STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj Nakon tranzicije nastupa turbulentni granični sloj koji ima bitno složeniju strukturu. Veći dio graničnog sloja sačinjen je od turbulentne zone sa vrtlozima i fluktuacijom parametara strujanja. U neposrednoj blizini zida fluktuacije su prigušene te prevladavaju laminarni uvjeti strujanja (viskozni podsloj).

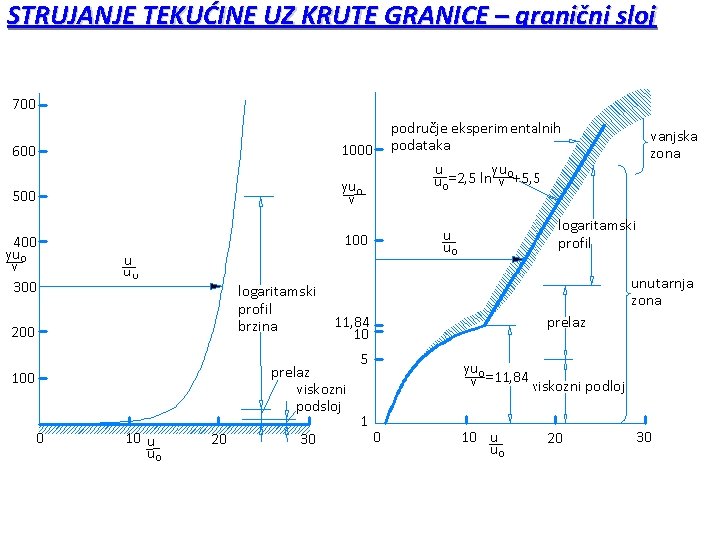
STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj U najvećem dijelu graničnog sloja pojavljuje se konstantno posmično naprezanje 0. U blizini slobodnog toka dolazi do naglijeg pada posmičnih naprezanja prema vrijednosti 0. Uvodi se pojam „brzinskog naprezanja“ izraženog sa: U području viskoznog podsloja odvija se čisto laminarno strujanje s linearnim profilom brzina u = ( 0 / ) y. U turbulentnom području graničnog sloja izmjena količine gibanja se ostvaruje uglavnom kroz djelovanje vrtloga (fluktuacije u trenutnim profilima brzina).

STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj Detaljnijom analizom dobiva se logaritamski zakon raspodjele brzina: - Karmanova konstanta = 0, 4 C - konstanta integracije u funkciji rubnih uvjeta Vrijednosti konstante C razlikuju se po karakterističnim područjima unutar turbulentne zone graničnog sloja: Za unutarnju turbulentnu zonu (zona sa utjecajem viskoznosti): 30 < y / l < 500

STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj Prijelaz iz linearnog zakona važećeg za viskozni podsloj u logaritamski zakon odvija se u prelaznom području 5 < y / l < 30 Za vanjsku turbulentnu zonu (zona bez utjecaja viskoznosti): y / l > 500 Za praktičnu upotrebu često se koristi jednostavniji izraz za profil brzina u širem rasponu Re brojeva: 85% graničnog sloja sadržano je u vanjskoj turbulentnoj zoni

STRUJANJE TEKUĆINE UZ KRUTE GRANICE – granični sloj

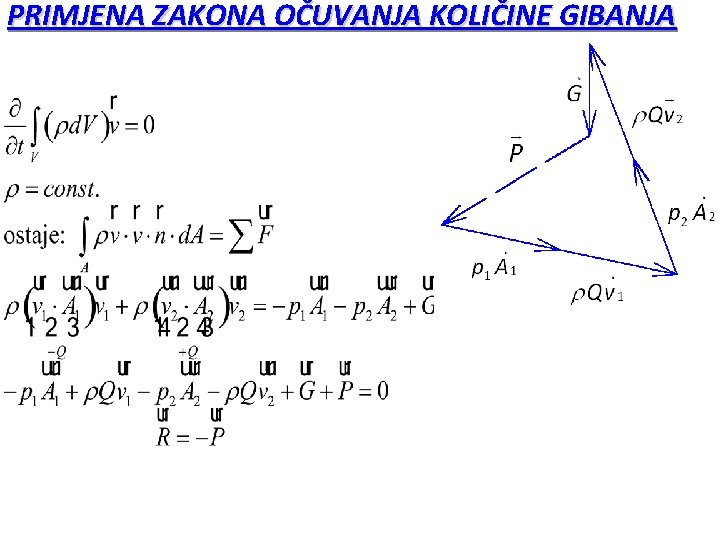
PRIMJENA ZAKONA OČUVANJA KOLIČINE GIBANJA Koristan alat u inženjerskim zadaćama određivanja sila na tekućinu u kontrolnom volumenu, bez da su poznati detalji o polju strujanja unutar samog kontrolnog volumena. Izvodi se integracija Navier-Stokes jednadžbe na zatvorenom kontrolnom volumenu (sapnica) s fokusom na iznalažanje rezultantnih sila, a ne pojedinačnih naprezanja (tlak, viskozna naprezanja).

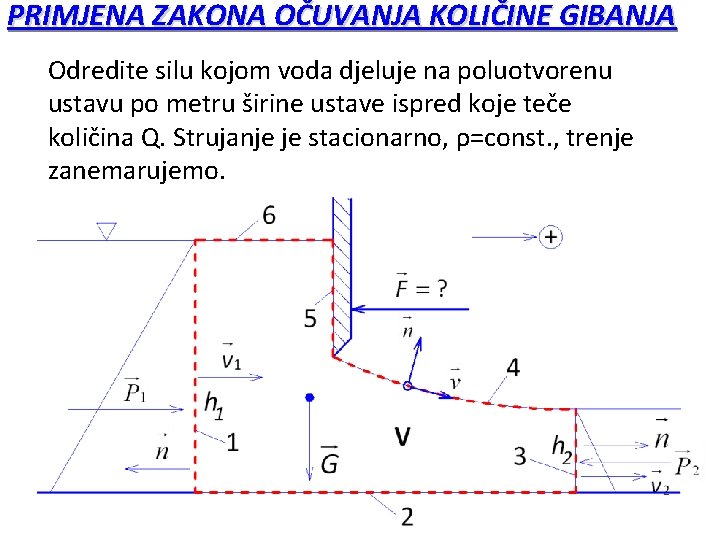
PRIMJENA ZAKONA OČUVANJA KOLIČINE GIBANJA Odredite silu kojom voda djeluje na poluotvorenu ustavu po metru širine ustave ispred koje teče količina Q. Strujanje je stacionarno, ρ=const. , trenje zanemarujemo.

PRIMJENA ZAKONA OČUVANJA KOLIČINE GIBANJA

PRIMJENA ZAKONA OČUVANJA KOLIČINE GIBANJA

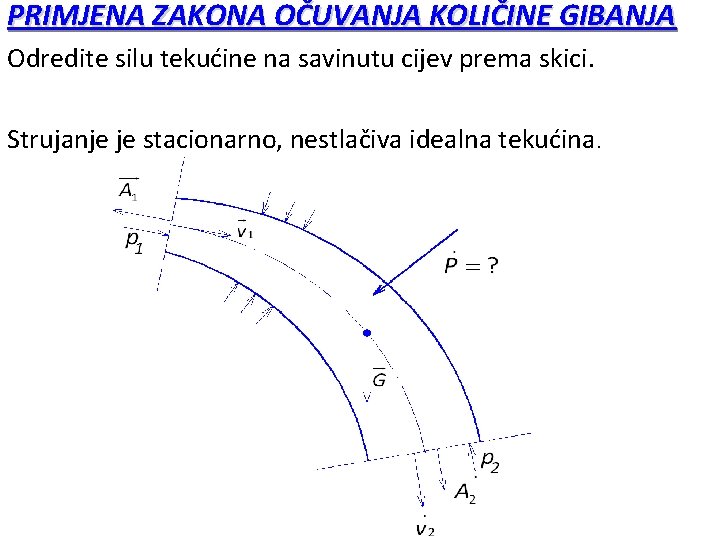
PRIMJENA ZAKONA OČUVANJA KOLIČINE GIBANJA Odredite silu tekućine na savinutu cijev prema skici. Strujanje je stacionarno, nestlačiva idealna tekućina.

PRIMJENA ZAKONA OČUVANJA KOLIČINE GIBANJA

BERNOULLIJEVA JEDNADŽBA- IDEALNA TEKUĆINA Koristan alat u inženjerskim zadaćama određivanja tlakova i srednjih brzina. Predstavlja jednadžbu bilance energije položaja i tlaka te kinetičke energije. U slučaju primjene BJ za idealnu tekućinu usvaja se pretpostavka o beviskoznosti, bezvrtložnosti i stacionarnosti. Usvajanjem bezviskoznosti Navier-Stokes jednadžba transformira se u Eulerovu jednadžbu: Za izvod Bernoullijeve jednadžbe poslužiti će nam Eulerova jednadžba za z komponentu:

BERNOULLIJEVA JEDNADŽBA- IDEALNA TEKUĆINA U slučaju bezvrtložnog strujanja iščezavaju članovi koji sadrže pa se za w komponentu strujanja nestišljive tekućine može pisati:

BERNOULLIJEVA JEDNADŽBA- IDEALNA TEKUĆINA Bernoullijeva funkcija je konstantna za z smjer, te uzduž strujnice i u smjeru okomito na nju: Bernoullijevom jednadžbom omogućeno je praćenje i usporedba različitih stanja strujanja uzduž strujnice te procjena promjene stanja strujanja. z (energija položaja) + p/ g (energija tlaka) = PL PL + v 2/2 g (kinetička energija) = EL

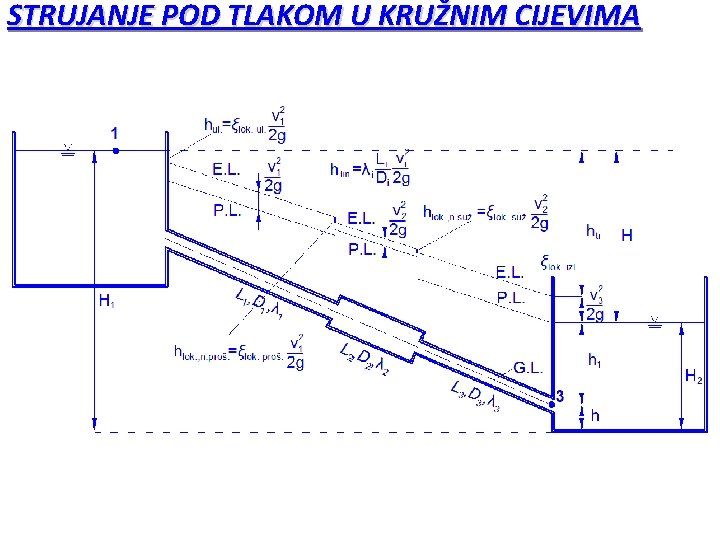
STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA Nema slobodnog vodnog lica (nestišljiva Newtonova tekućina). Analiziramo stacionarna stanja. Geometrija cjevovoda definirana je promjerom cijevi D i duljinom cijevi L. Usvaja se pretpostavka L>>D. Stoga je zanemaren utjecaj “početne” dionice cijevi u kojem se poprečni profil brzina strujanja tek “razvija” do svog konačnog oblika. Naprezanja (trenje) koje se neminovno pojavljuje na kontaktu s krutom stjenkom može se definirati izrazom:

STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA Naprezanje W potrebno je “svladati” u cilju održanja gibanje tekućine kroz cijev sustava. Želimo odrediti i raspodjelu naprezanja u poprečnom presjeku cijevi te empiričke odnose između tih naprezanja i brzina. Raspodjela naprezanja definirana je linearnim zakonom promjene (okomito na os cijevi):

STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA Pri jednolikom strujanju (du/ds=0 ; konzervativna cijev konstantnog proticajnog presjeka) ne mijenja se naprezanje W u smjeru strujanja. Stoga se ne mijenjaju ni gradijenti PL i EL. Razina energetske linije na poziciji 2 je manja za ELIN (linijski gubitak mehaničke energije) u odnosu na poziciju 1, neovisno o samoj poziciji EL ili PL (iznad ili ispod osi cijevi).

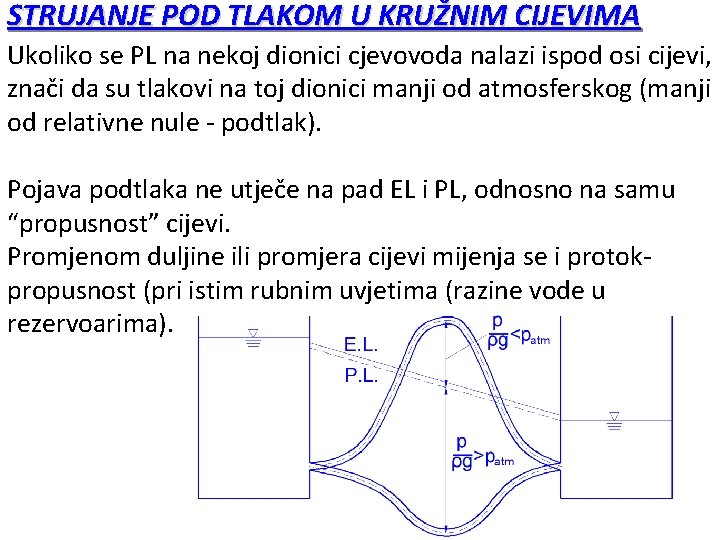
STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA Ukoliko se PL na nekoj dionici cjevovoda nalazi ispod osi cijevi, znači da su tlakovi na toj dionici manji od atmosferskog (manji od relativne nule - podtlak). Pojava podtlaka ne utječe na pad EL i PL, odnosno na samu “propusnost” cijevi. Promjenom duljine ili promjera cijevi mijenja se i protokpropusnost (pri istim rubnim uvjetima (razine vode u rezervoarima).

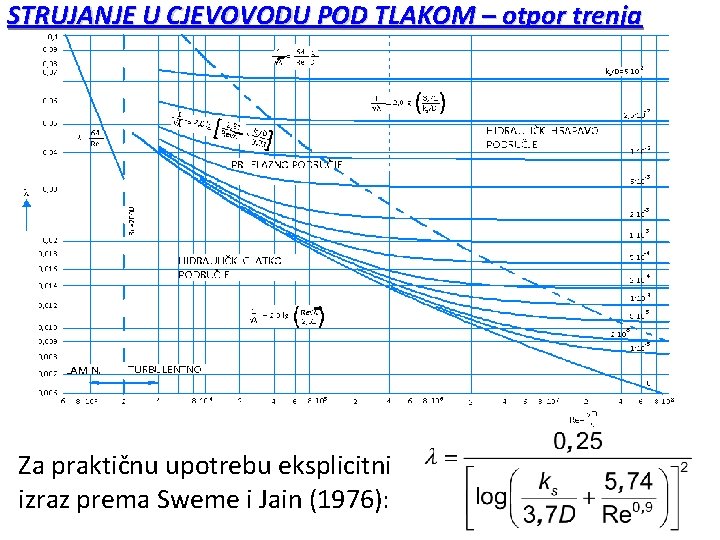
STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA Vrijednost linijskog gubitaka ELIN za cijev kružnog profila s promjerom D i duljine L može se odrediti temeljem Darcy. Weisbach koeficijenta otpora (trenja) . Odnos koeficijenta otpora i naprezanja uz samu stjenku cijevi w definiran je izrazom: Koeficijent je u općem slučaju funkcija Re (Reynoldsov broj i /D (relativna hrapavost). U laminarnom strujanju = f (Re)= 64/Re (za Re<2300)

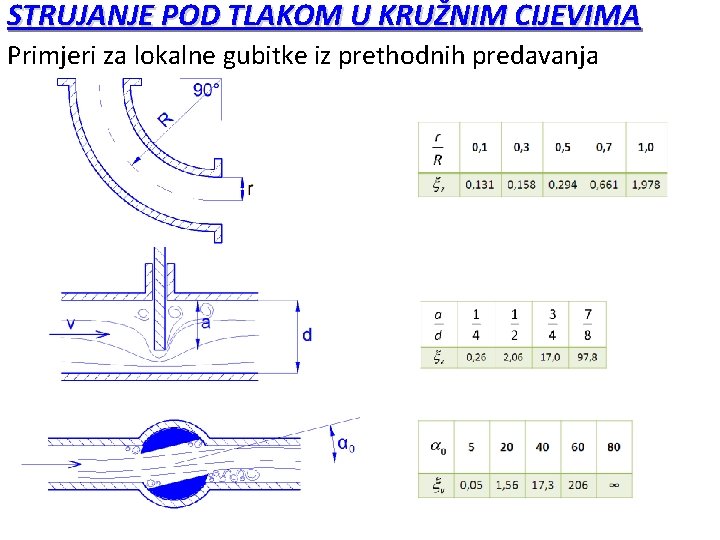
STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA U turbulentnom režimu (Re>2300) nema analitičkog rješenja Navier-Stokes jednadžbe te se za koriste eksperimentalni podaci (Moodyjev dijagram). U prelaznom režimu = f (Re, /D) dok je u turbulentnohrapavom režimu = f ( /D). Osim linijskih gubitaka pojavljuju se i lokalni gubici ELOK mehaničke energije, inducirani promjenom geometrije toka odnosno krutih granica (suženja, proširenja, račve, zatvarači). Kao i u slučaju linijskih gubitaka, lokalni gubici se proračunavaju vezano na kinetičku energiju (član v 2/2 g). vrijednosti koeficijenata lokalnih gubitaka dobivaju se iz eksperimenata.

STRUJANJE U CJEVOVODU POD TLAKOM – otpor trenja Za praktičnu upotrebu eksplicitni izraz prema Sweme i Jain (1976):

STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA Primjeri za lokalne gubitke iz prethodnih predavanja

STRUJANJE POD TLAKOM U KRUŽNIM CIJEVIMA

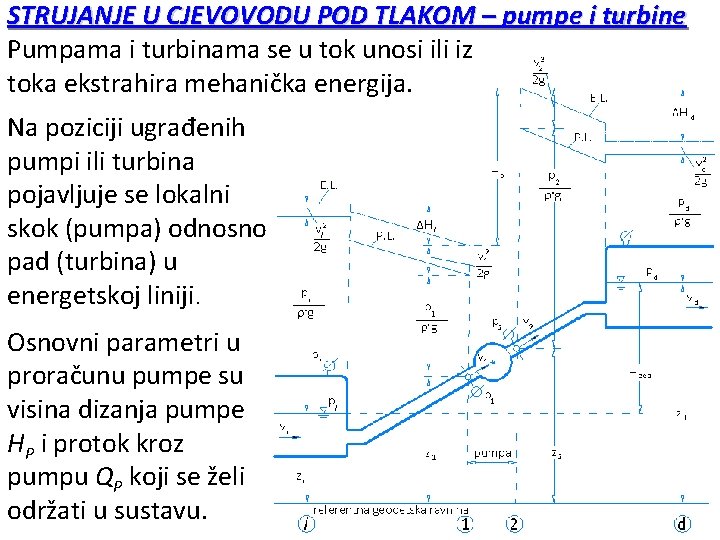
STRUJANJE U CJEVOVODU POD TLAKOM – pumpe i turbine Pumpama i turbinama se u tok unosi ili iz toka ekstrahira mehanička energija. Na poziciji ugrađenih pumpi ili turbina pojavljuje se lokalni skok (pumpa) odnosno pad (turbina) u energetskoj liniji. Osnovni parametri u proračunu pumpe su visina dizanja pumpe HP i protok kroz pumpu QP koji se želi održati u sustavu.

STRUJANJE U CJEVOVODU POD TLAKOM – pumpe i turbine Primjena Bernoullijeve jednadžbe za strujanje realne tekućine u sustavu pod tlakom daje rješenje za vrijednost dizanja pumpe HP: razlika geodetskih razina slobodnih vodnih lica u lijevoj i desnoj komori razlika tlačne razlika kinetičke energije u lijevoj i desnoj komori (veliki spremnici -brzine imaju vrijednosti 0) suma gubitaka mehaničke energije od presjeka „ 2“ do „d“ suma gubitaka mehaničke energije od presjeka „l“ do „ 1“ Potrebna snaga pumpe definirana je izrazom: - stupanj efikasnosti prenosa snage pumpe na proticajnu tekućinu ( uvijek manji od 1).

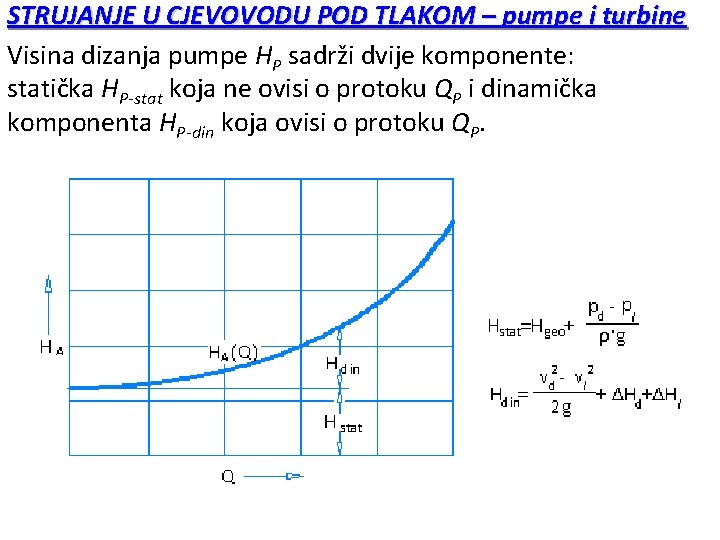
STRUJANJE U CJEVOVODU POD TLAKOM – pumpe i turbine Visina dizanja pumpe HP sadrži dvije komponente: statička HP-stat koja ne ovisi o protoku QP i dinamička komponenta HP-din koja ovisi o protoku QP.

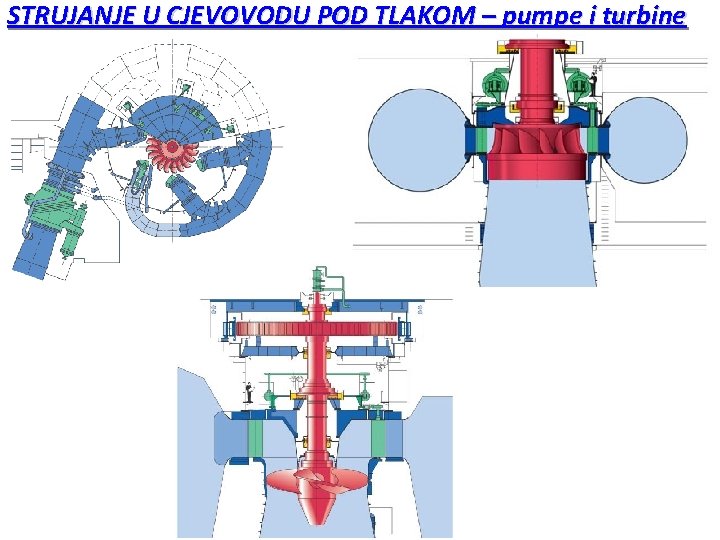
STRUJANJE U CJEVOVODU POD TLAKOM – pumpe i turbine Turbine se između ostalog pojavljuju i u objektima namijenjenim za korištenje vodnih snaga. Ovisno o raspoloživoj razlici potencijala gornje i donje vode usporni objekti (brane) dijele se na niskotlačne, srednje i visokotlačne. Karakteristične vrijednosti razlika razina donje i gornje vode H nalaze se u rasponu: - Niskotlačno postrojenje H < 15 m - Srednjetlačno postrojenje H = 15 -50 m - Visokotlačno postrojenje H > 50 m

STRUJANJE U CJEVOVODU POD TLAKOM – pumpe i turbine Ugrađuju se različiti tipovi turbina u ovisnosti o raspoloživoj razlici potencijala gornje i donje vode. Tip turbine pad HT[m] Pelton 2000 -100 Francis 150 -80 Kaplan i cijevne turbine 80 -2 Snaga koja se ostvaruje radom turbine izražava se na način: - stupanj efikasnosti prenosa snage pumpe na proticajnu tekućinu ( uvijek manji od 1).

STRUJANJE U CJEVOVODU POD TLAKOM – pumpe i turbine

POTENCIJALNO STRUJANJE Potencijalna teorija je linearna. Analiziramo samo 2 D strujanje nestišljive ( = 0), bezviskozne ( = 0) i bezvrtložne ( = = 0) tekućine. Iz zadnjeg uvjeta ( = 0) proizlazi da je polje strujanja u svim točkama prostora definirano gradijentom brzinskog potencijala . Daljnjom primjenom jednadžbe kontinuiteta dobiva se: Slično vrijedi i za strujnu funkciju ( = 0 =0)

POTENCIJALNO STRUJANJE U svakoj točci strujnog polja zadovoljen je uvjet ortogonalnosti ekvipotencijala (linije istog potencijala) i strujnica (linije iste vrijednosti strujne funkcije). Ekvipotencijale i strujnice zajednički tvore strujnu mrežu. Uzduž ekvipotencijele nema pronosa mase (strujanja) a rubovi krute (nepropusne) granice mogu se opisati “rubnom” strujnicom. Teorija potencijalnog strujanja razvijena je s ciljem iznalaženja analitičkih rješenja za pojedine slučajeve strujanja u zoni gdje su smisaone usvojene pretpostavke ( = 0 ; = 0).

POTENCIJALNO STRUJANJE Pretpostavke potencijalnog strujanja zadovoljene su primarno u zoni konvergentnog (ubrzavajućeg) strujanja, u kojoj dolazi do održavanja tankog graničnog sloja u blizini krute stijenke. Divergentno (usporavajuće) strujanje s povećanjem tlaka uzduž toka dovodi do separacije (odvajanja) graničnog sloja od čvrste konture. Male brzine strujanja nisu uvjet za smisaonu primjenu ideje (modela) potencijalnog strujanja. Analiza strujanja podzemnih voda (male brzine) temelji se na potencijalnom strujanju. Prelijevanje preko preljeva ili opstrujavanje krilnih profila (velike brzine) također se učestalo analizirala potencijalnim strujanjem.

POTENCIJALNO STRUJANJE Prvotno se iznalazi potencijal , te iz njega brzine strujanja. Budući je Laplaceova jednadžba linearna, moguća je primjena principa superpozicije elementarnih rješenja strujanja. Uobičajena elementarna rješenja se odnose na slučajeve: Paralelno strujanje:

POTENCIJALNO STRUJANJE Strujanje ka ponoru i od izvora: Q je mjera izdašnosti izvora a -Q izdašnosti ponora. Uvjet = 0 (jednadžba kontinuiteta) narušen je u točki singulariteta (ishodište)

POTENCIJALNO STRUJANJE Potencijalni vrtlog: je mjera cirkulacije (+ znači vrtnju u desnu stranu). Uvjet = 0 (jednadžba kontinuiteta) narušen je u točki singulariteta (ishodište)

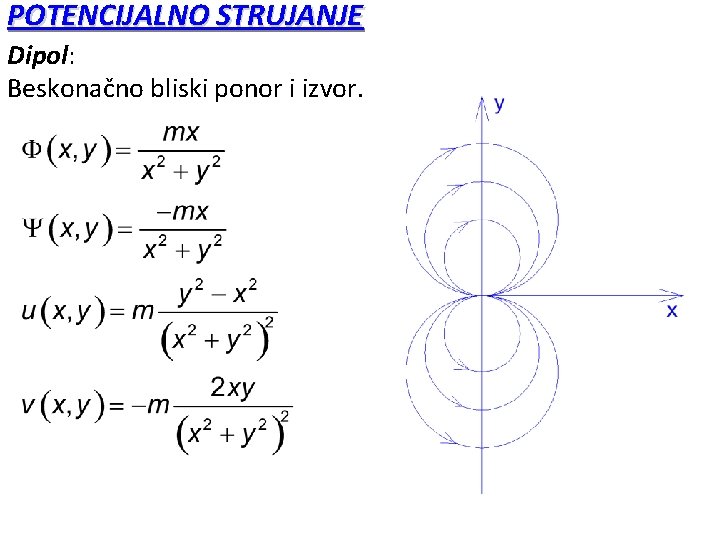
POTENCIJALNO STRUJANJE Dipol: Beskonačno bliski ponor i izvor.