Zaawansowane metody analizy sygnaw Dr in Cezary Maj

Zaawansowane metody analizy sygnałów Dr inż. Cezary Maj Dr inż. Piotr Zając Katedra Mikroelektroniki i Technik informatycznych PŁ

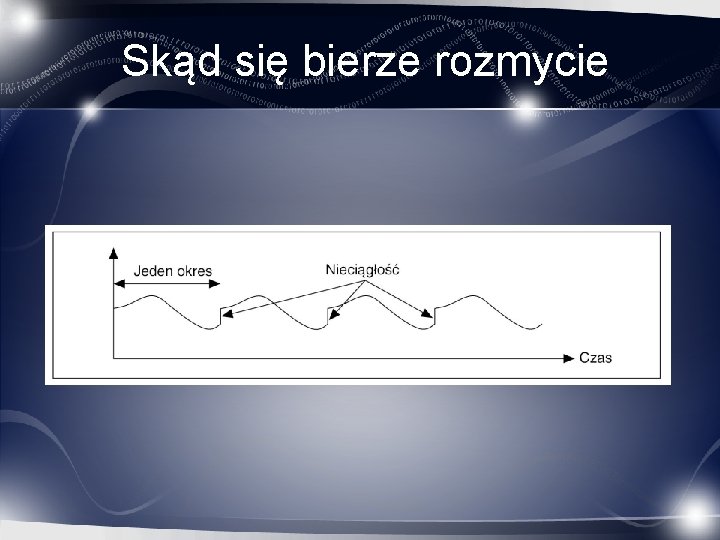
Rozmycie widma polega na obserwacji niezerowych wartości dla częstotliwości innej niż faktyczna czestotliwość sygnału.

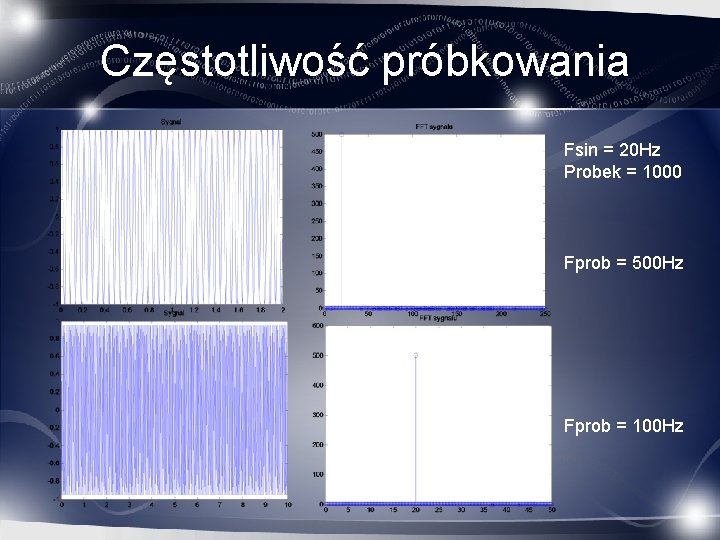
Częstotliwość próbkowania Fsin = 20 Hz Probek = 1000 Fprob = 500 Hz Fprob = 100 Hz

Liczba próbek Fsin = 20 Hz Fprob = 500 Hz probek = 50 Fprob = 25

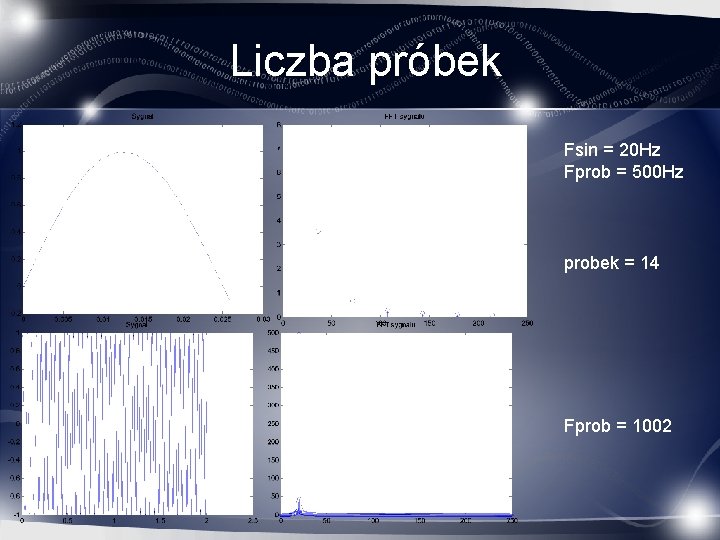
Liczba próbek Fsin = 20 Hz Fprob = 500 Hz probek = 14 Fprob = 1002

Skąd się bierze rozmycie

Okna czasowe Funkcja służąca zmniejszeniu wpływu „niedopasowania” parametrów próbkowania. Metoda okien czasowych polega na wymnożeniu sygnału cyfrowego przez okno czasowe.

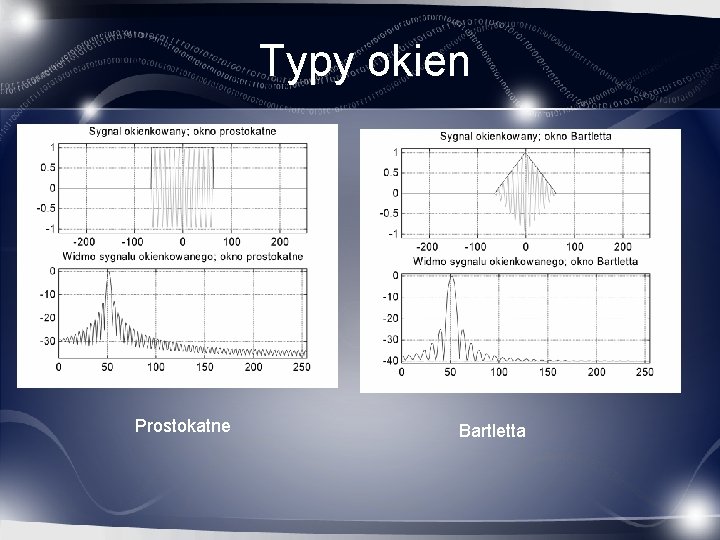
Typy okien Prostokatne Bartletta

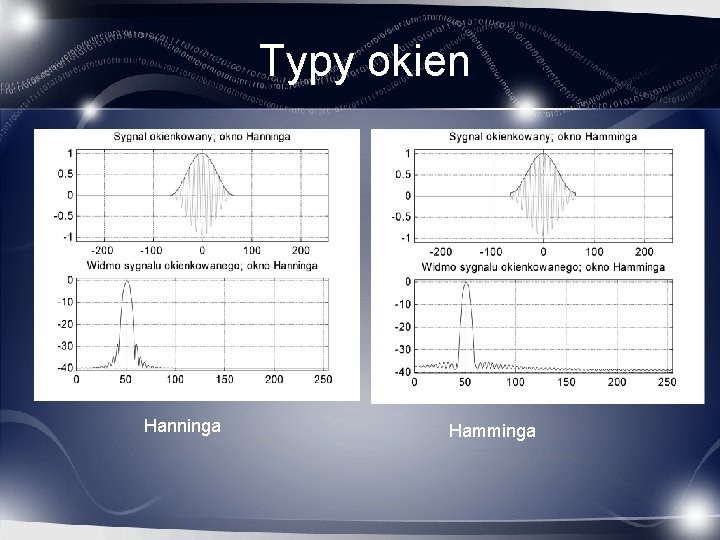
Typy okien Hanninga Hamminga

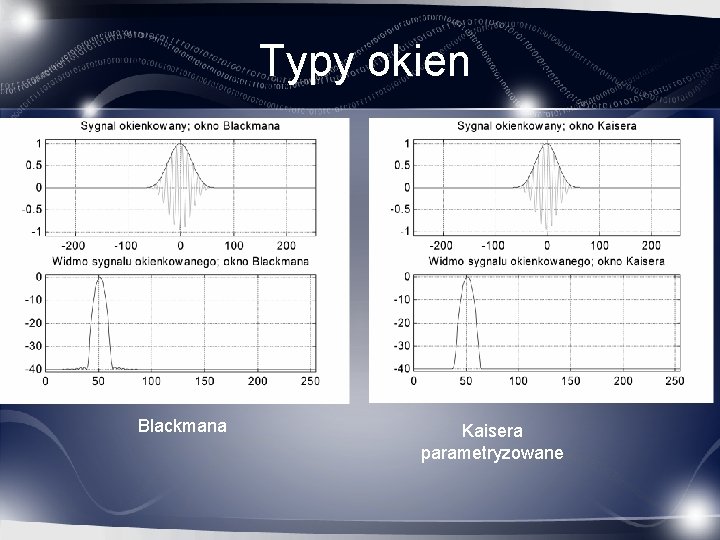
Typy okien Blackmana Kaisera parametryzowane

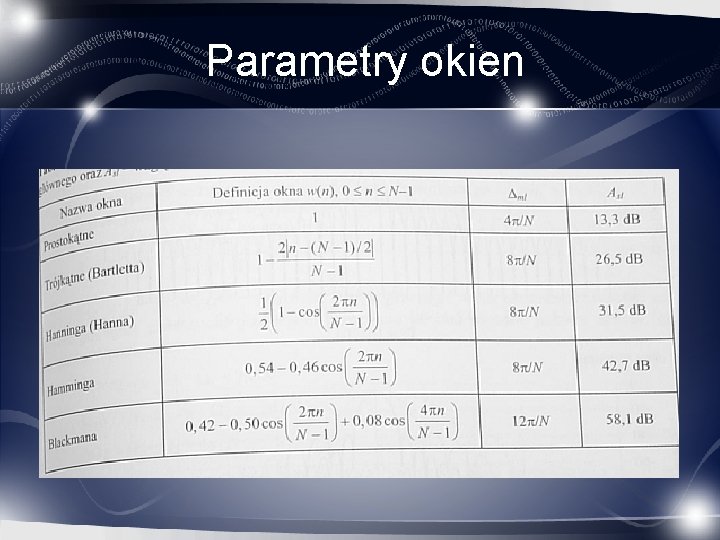
Parametry okien

Wpływ nałożenia okna Szerokość listka głównego widma okna wpływa na rozróżnialność częstotliwościową DFT (jeżeli różnica częstotliwości dwóch składowych jest mniejsza od szerokości listka głównego, to odpowiadające im prążki zleją się w jeden wskutek rozmycia widma. Wysokość listków bocznych widma okna wpływa na rozróżnialność amplitudową DFT (jeżeli w sygnale występuje składowa o amplitudzie porównywalnej z amplitudą lisków bocznych, to „utonie” ona w pofalowaniach widma.

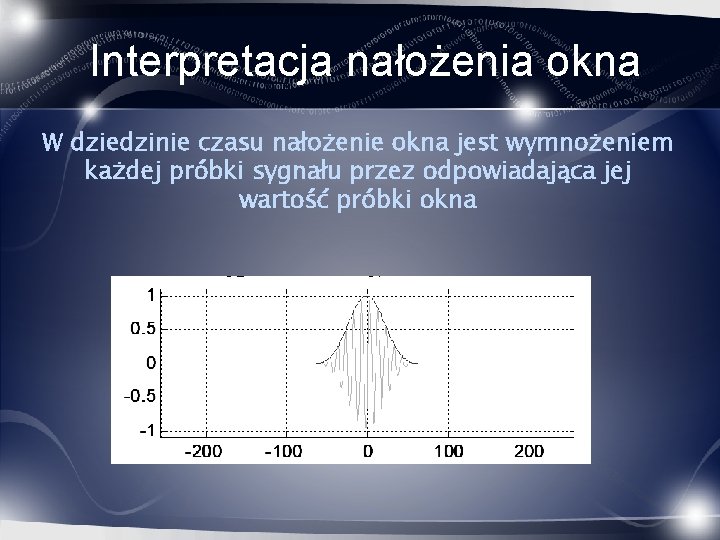
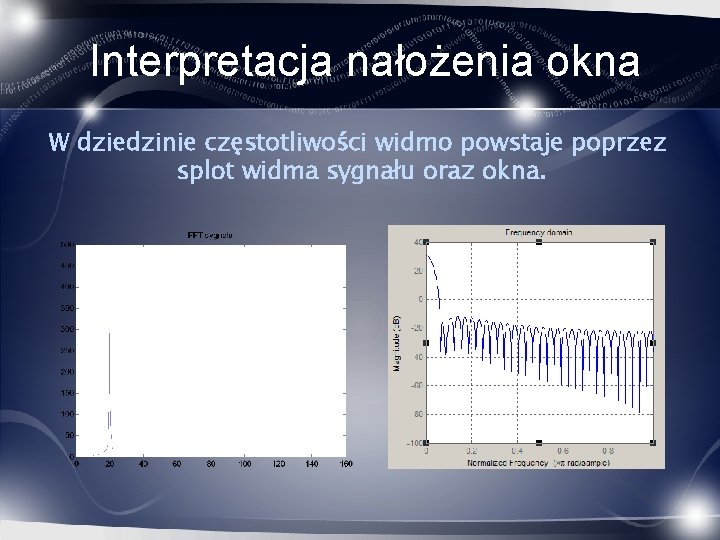
Interpretacja nałożenia okna W dziedzinie czasu nałożenie okna jest wymnożeniem każdej próbki sygnału przez odpowiadająca jej wartość próbki okna

Interpretacja nałożenia okna W dziedzinie częstotliwości widmo powstaje poprzez splot widma sygnału oraz okna.

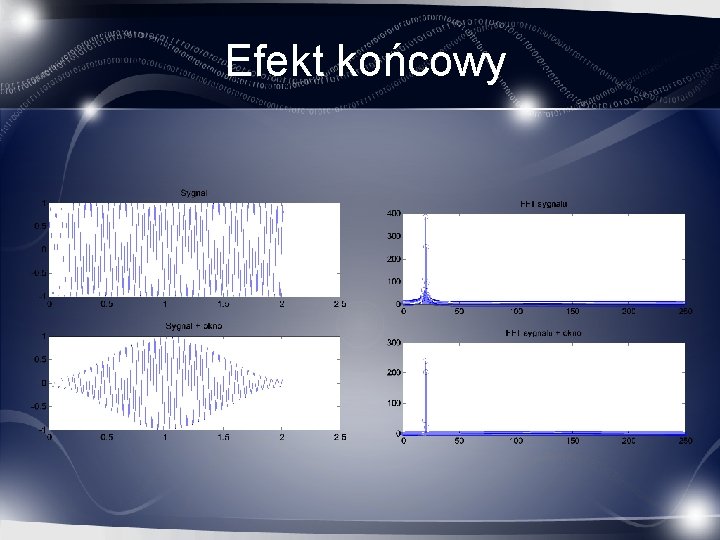
Efekt końcowy

Szybka transformata Fouriera Nakład obliczeniowy: • 2 N 2 mnożeń • 2(N-1)2 sumowań Możliwe sposoby optymalizacji: • Lustro widma • Powtarzające się obliczenia

Idea FFT Podział ciągu N-punktowego na dwa N/2 -punktowe • Oszczędność 2 N 2 2(N/2)2 2 N 2 /4 mnożeń • 2(N-1)2 2(N/2 -1)2 2(N-2)2 /2 sumowań Możliwe sposoby optymalizacji: • Lustro widma • Powtarzające się obliczenia

Idea FFT

Idea FFT

FFT w praktyce dekompozycja

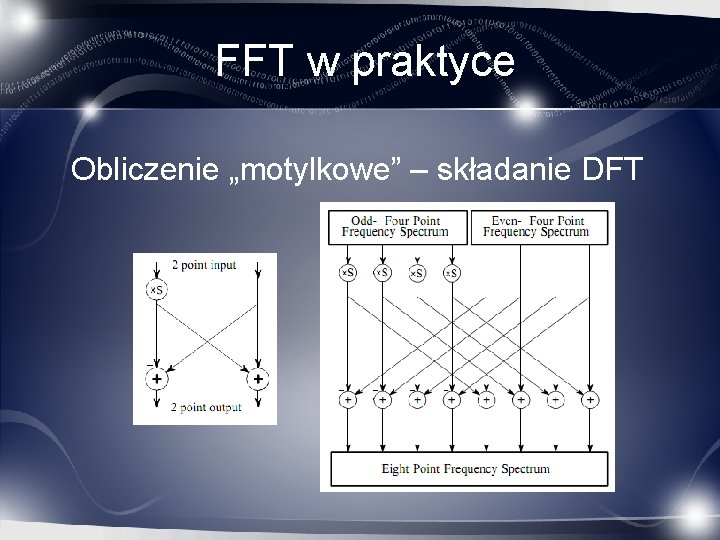
FFT w praktyce Obliczenie „motylkowe” – składanie DFT

FFT w praktyce Pełny schemat blokowy

FFT w praktyce

FFT w praktyce

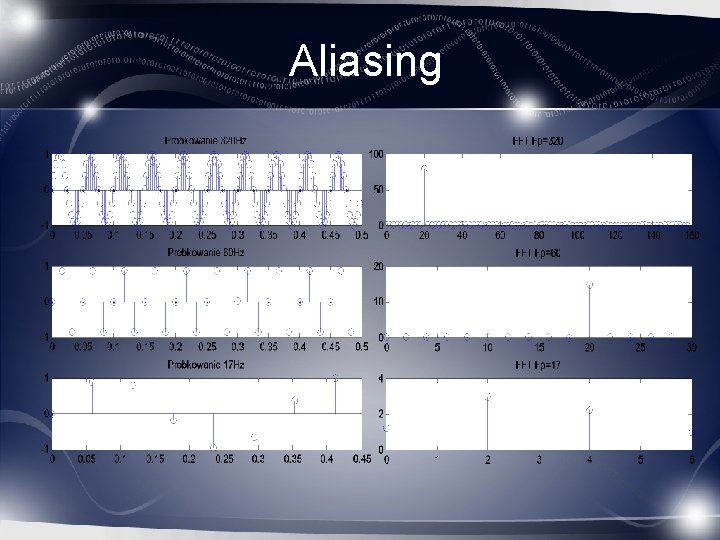
Aliasing Nieodwracalne zniekształcenie sygnału w procesie próbkowania wynikające z niespełnienia warunków twierdzenia Kotelnikowa-Shannona

Aliasing

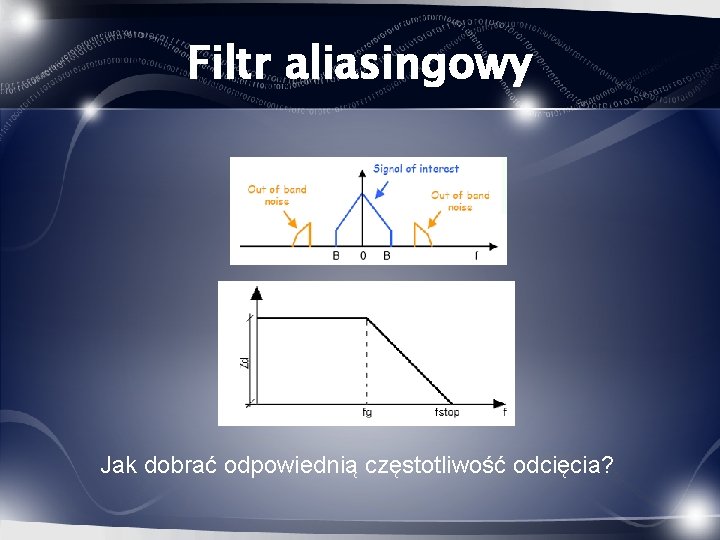
Filtr aliasingowy

Filtr aliasingowy Jak dobrać odpowiednią częstotliwość odcięcia?

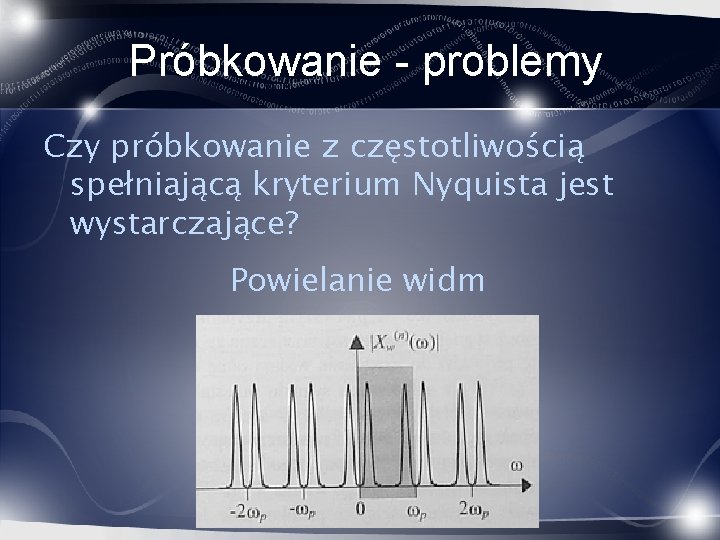
Próbkowanie - problemy Czy próbkowanie z częstotliwością spełniającą kryterium Nyquista jest wystarczające? Powielanie widm

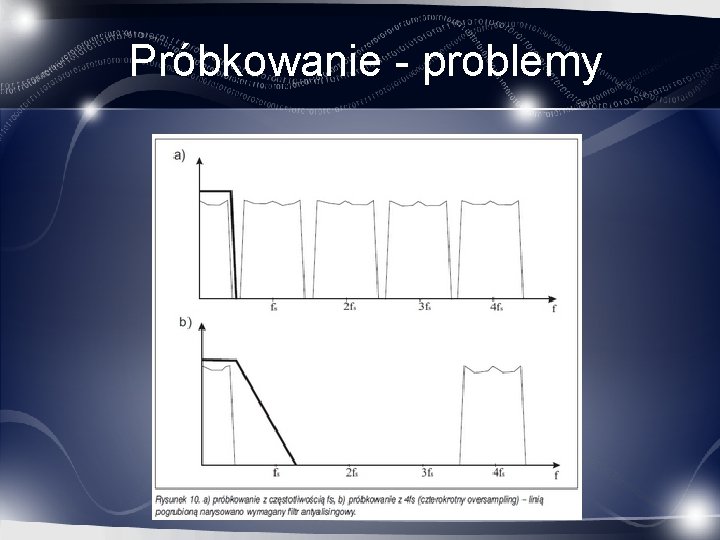
Próbkowanie - problemy

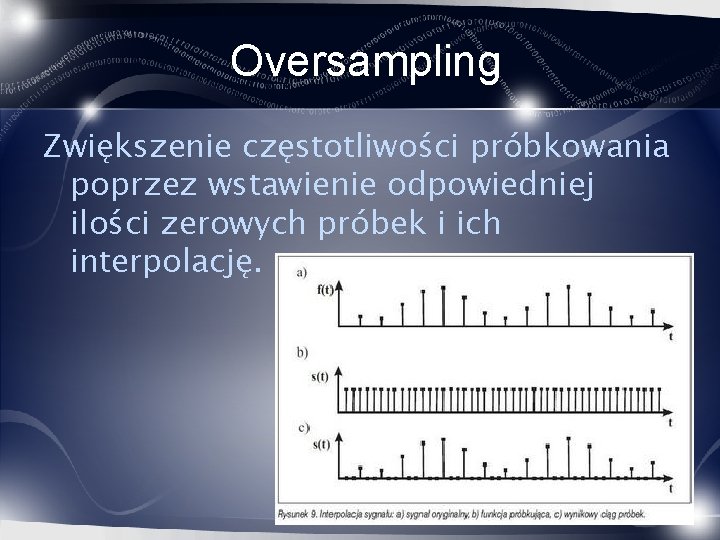
Oversampling Zwiększenie częstotliwości próbkowania poprzez wstawienie odpowiedniej ilości zerowych próbek i ich interpolację.

Rekonstrukcja sygnału Rekonstrukcja polega na wykonaniu operacji interpolacji.

Rekonstrukcja sygnału Idealna rekonstrukcja – przefiltrowanie przez idealny filtr

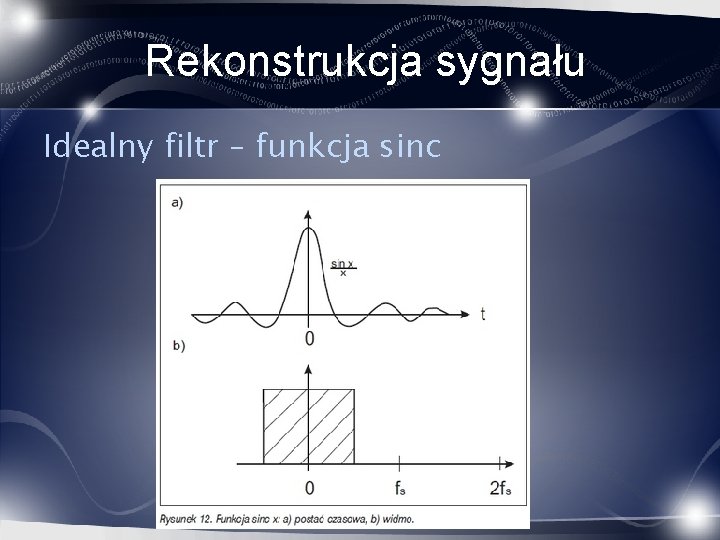
Rekonstrukcja sygnału Idealny filtr – funkcja sinc

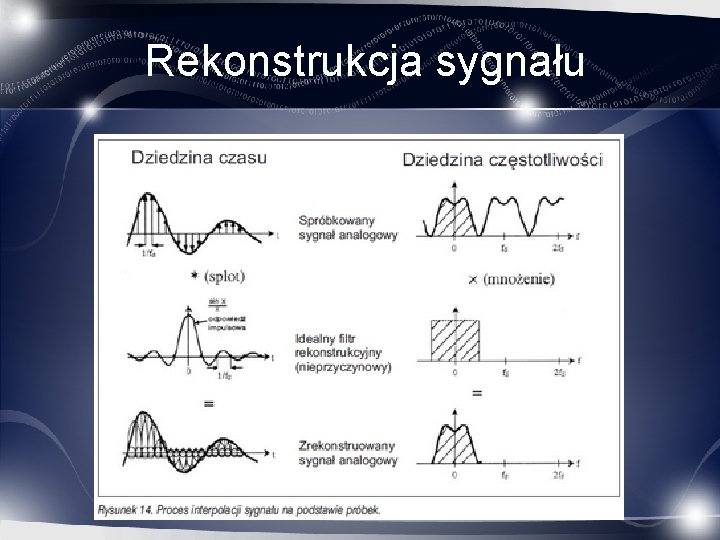
Rekonstrukcja sygnału Wymnożenie widm jest równoznaczne ze splotem w dziedzinie czasu

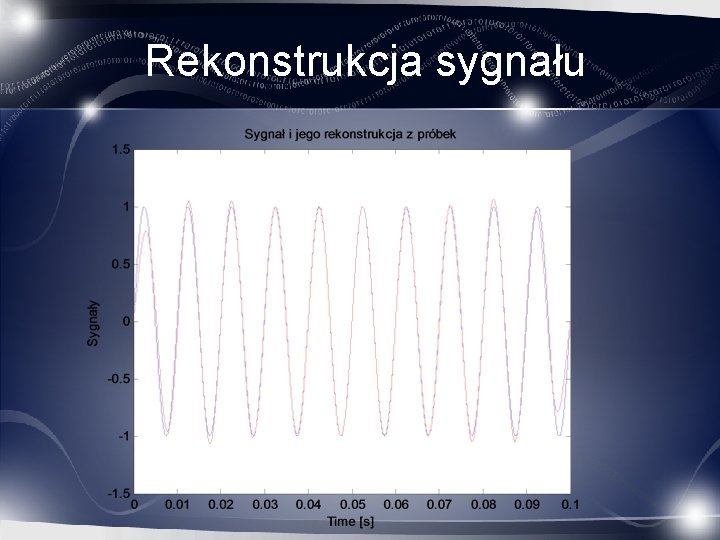
Rekonstrukcja sygnału

Rekonstrukcja sygnału