Z transform Defined as power series Examples 1

Z - transform • Defined as power series • Examples: 1

Z - transform • And since • We get 2

Z - transform • Define +ve and > 1 +ve and = 1 +ve and < 1 3

Z - transform • We have • ie • Note that has a pole at on the zplane. 4

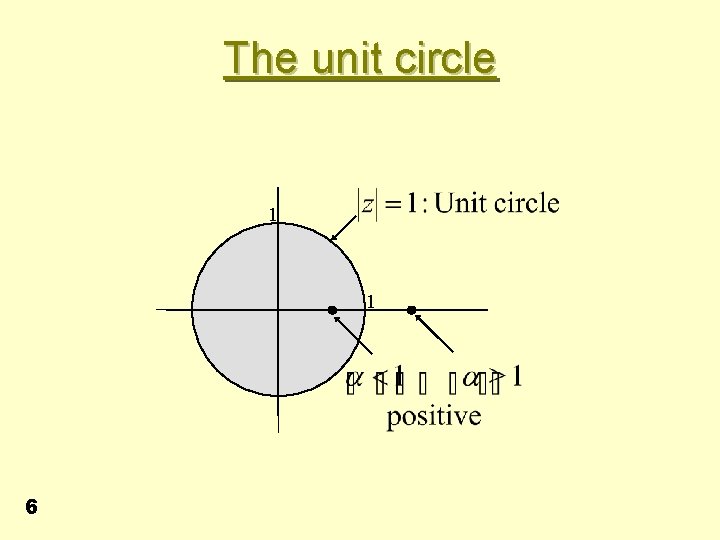
Z - transform Note: • (i) If magnitude of pole is > 1 then increases without bound • (ii) If magnitude of pole is < 1 then has a bounded variation • i. e. the contour on the z-plane is of crucial significance. • It is called the Unit circle 5

The unit circle 1 1 6

Z – transform properties (i) Linearity • The z-transform operation is linear • Z • Where Z (ii) Shift Theorem Z 7 , i = 1, 2

Z - transform • Let. . • Z • But 8 for negative i.

Z - transform Examples: • (i) Consider generation of new discrete time signal from via • Recall linearity and shift • (ii) Z write 9

Z - transform • From • With from earlier result Z • We obtain Z 10

Inverse Z - transform • Given F(z) to determine . • Basic relationship is • may be obtained by power series expansion. It suffers from cumulative errors 11

Inverse Z - transform • Alternatively • Use for m = -1 • otherwise • where closed contour encloses origin 12

Inverse Z - transform • Integrate to yield Examples • (i) write 13

Inverse Z - transform • And hence Pole at of Residue (ii) Let where and • To determine 14

Inverse Z - transform • From inversion formula • But 15

Inverse Z - transform • Hence • Thus 16

Inverse Z - transform Note: • (i) For causal signals for negative i. Thus upper convolution summation limit is in this case equal to k. • (ii) Frequency representation of a discretetime signal is obtained from its z-transform by replacing where T is the sampling period of interest. (Justification will be given later. ) 17

System Function of discretetime systems • System representation {x(n)} X(z) {h(n)} G(z) {y(n)} Y(z) • Where the input signal is {x(n)} of ztransform X(z) • The output is {y(n)} of z-transform Y(z). 18

System Function of discretetime systems • The system has an impulse response h(n) • Define so that and hence 19 • Clearly when X(z) = 1 then G(z) = Y(z) i. e. G(z) is the z-transform of the impulse response h(n)

Frequency Response • Let the input be • Then the output is • Where • and 20

System Function of discretetime systems • However • While the amplitude & phase responses are • And hence 21

System Functions-Amplitude response • Evidently 22 • And hence • Thus • ie for real systems amplitude is an even function, and phase an odd function of frequency

System Functions-Amplitude response • Moreover from • Since at is finite we obtain 23

System Functions-Phase response • From • At we have • Thus for real systems the amplitude response must approach zero frequency with zero slope, while the phase rsponse must be zero at the origin 24

System Functions-Phase response • For , • Hence 25

System Functions-Group delay • Thus • where 26

Suppression of a frequency band • A real rational transfer function H(z) cannot suppress a band of frequencies completely. i. e. cannot be identically zero for in • This may be demonstrated as follows 27

System Function of discretetime systems • To produce a zero at say we must have in the numerator of H(z) a factor of the form • Therefore for one zero in the band the factor is • • and since there an infinite number of points in the band we need factors in the numerator as 28

System Function of discretetime systems • Clearly the result is not a rational function • Hence it cannot be the transfer function of a digital signal processing system. 29

Stability Test • For stability a DSP transfer function must have poles inside the unit circle on the zplane. • We need to have a means of determining whether the denominator of a given transfer function has all its zeros inside the unit circle. • The procedures for doing so are called stability tests. 30

Stability Test • Let the transfer function to be tested be • where n is the order of the transfer function. Set A = 1. • For stability Dn(z) must have no zeros in the region 31

Stability Test • Consider the simple case of a quadratic denominator • Rewrite as (ignore the factor ) • If the roots are complex, say then 32

Stability Test • Thus and • For stability and thus • For real roots • If choose root with largest absolute value and make less than 1 33

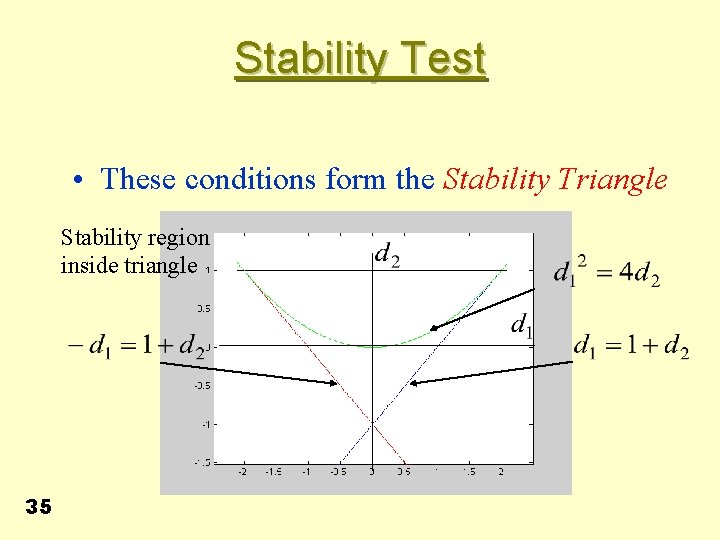
Stability Test • Thus • And since quantities are positive we obtain • Similarly for • Thus jointly we have 34

Stability Test • These conditions form the Stability Triangle Stability region inside triangle 35

Stability Test • For higher order functions most tests rely on an iterative precedure that involves – reduction of the polynomial degree by unity – a simple test • Jury-Marden Test: We write Dn(z) as 36 • where is a constant chosen to make of degree (n - 1)

Stability Test • • Repeat equation Hence And thus Set so that is of degree (n-1) when 37

Stability Test • Rouche’s Theorem: If the polynomials and are such that in the same region then has the same number of zeros in that region as 38

Stability Test • we observe that Dn(z) has as many zeros as either or depending on whether • or • Ie or 39

Stability Test • Thus if then is unstable as it has as many zeros as which has at most (n - 1) zeros within |z| < 1. • If then can have as many zeros within |z| < 1 as • The zero at z = 0 can be removed and the procedure repeated for the remaining polynomial 40

Stability Test • An alternative test: Consider • So that 41 • For this equation to be a polynomial we require the constant term in the numerator to be zero so as to be able to cancel through a factor z

Stability Test • Thus or • The rest of the argument is similar to the previous case 42

Further Stability Test • Given that and show that on the unit circle for any real • Construct • Repeat the previous arguments 43

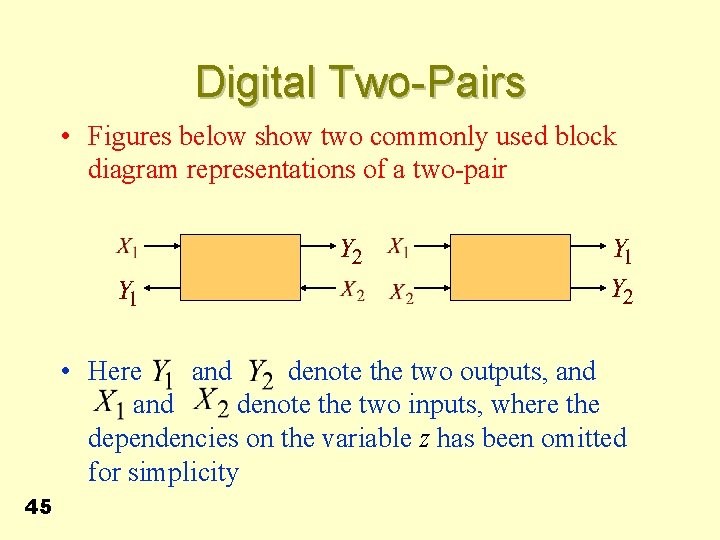
Digital Two-Pairs • The LTI discrete-time systems considered so far are single-input, single-output • Often such systems can be efficiently realised by interconnecting two-input, twooutput structures, known as two-pairs 44

Digital Two-Pairs • Figures below show two commonly used block diagram representations of a two-pair • Here and denote the two outputs, and denote the two inputs, where the dependencies on the variable z has been omitted for simplicity 45

Digital Two-Pairs • The input-output relation of a digital two-pair is given by • In the above relation the matrix t given by t is called the transfer matrix of the two-pair 46

Digital Two-Pairs • An alternate characterisation of the two-pair is in terms of its chain parameters as where the matrix G given by G - - is called the chain matrix of the two-pair 47

Digital Two-Pairs • The transfer and chain parameters are related as 48

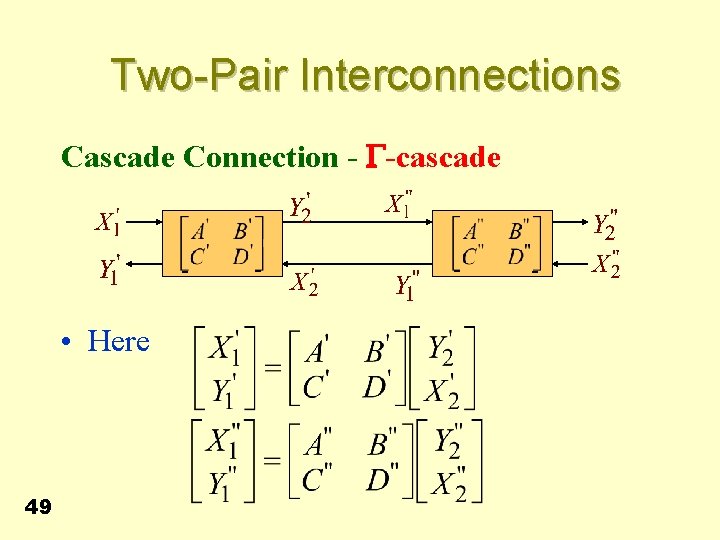
Two-Pair Interconnections Cascade Connection - G-cascade - • Here 49 - - -

Two-Pair Interconnections • But from figure, and • Substituting the above relations in the first equation on the previous slide and combining the two equations we get • Hence, 50

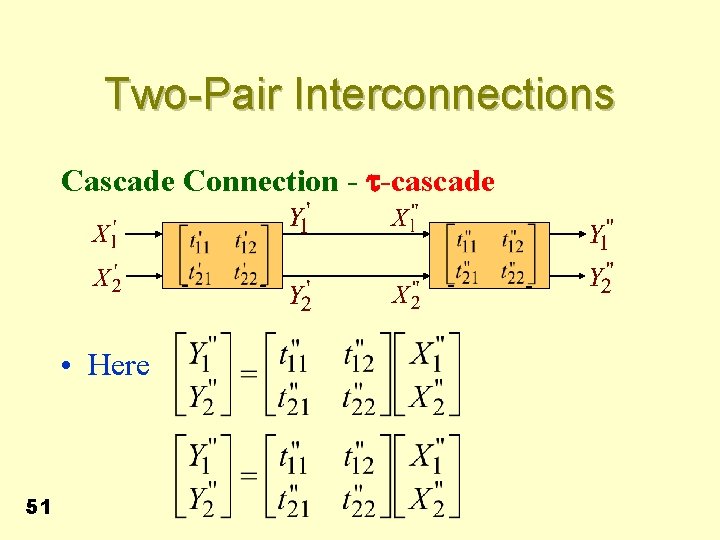
Two-Pair Interconnections Cascade Connection - t-cascade - • Here 51 - - -

Two-Pair Interconnections • But from figure, and • Substituting the above relations in the first equation on the previous slide and combining the two equations we get • Hence, 52

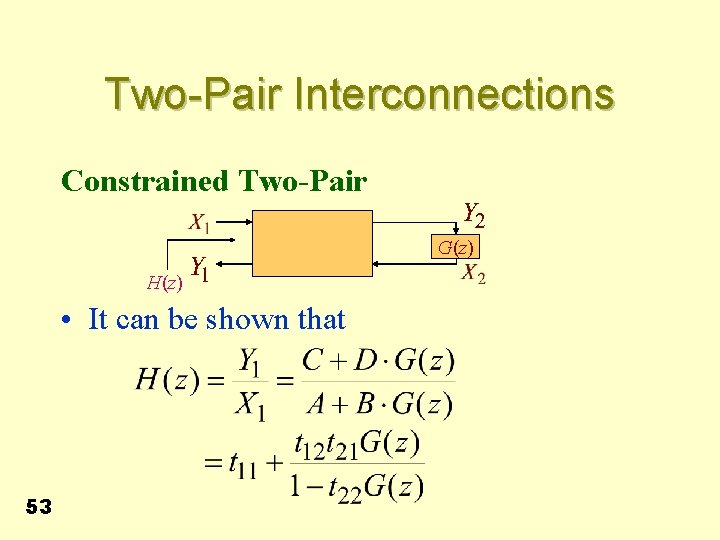
Two-Pair Interconnections Constrained Two-Pair G(z) H(z) • It can be shown that 53

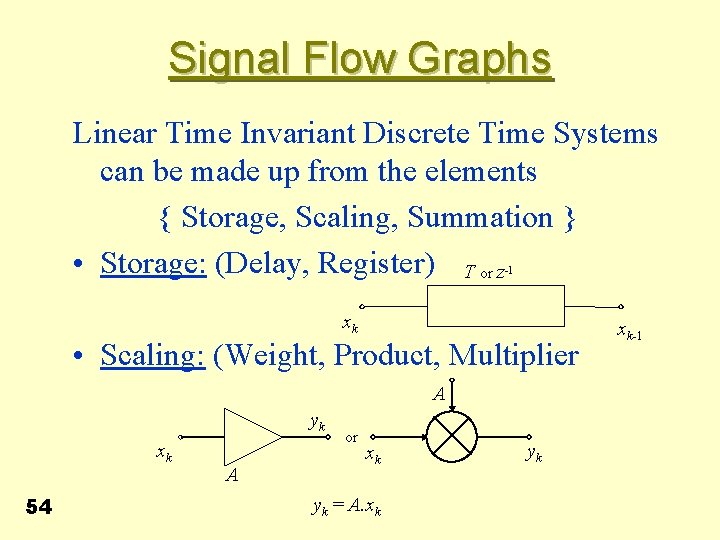
Signal Flow Graphs Linear Time Invariant Discrete Time Systems can be made up from the elements { Storage, Scaling, Summation } • Storage: (Delay, Register) T or z -1 xk • Scaling: (Weight, Product, Multiplier A yk xk 54 A or xk yk = A. xk yk xk-1

Signal Flow Graphs • Summation: (Adder, Accumulator) • + X X+Y + Y • A linear system equation of the type considered so far, can be represented in terms of an interconnection of these elements • Conversely the system equation may be obtained from the interconnected components (structure). 55

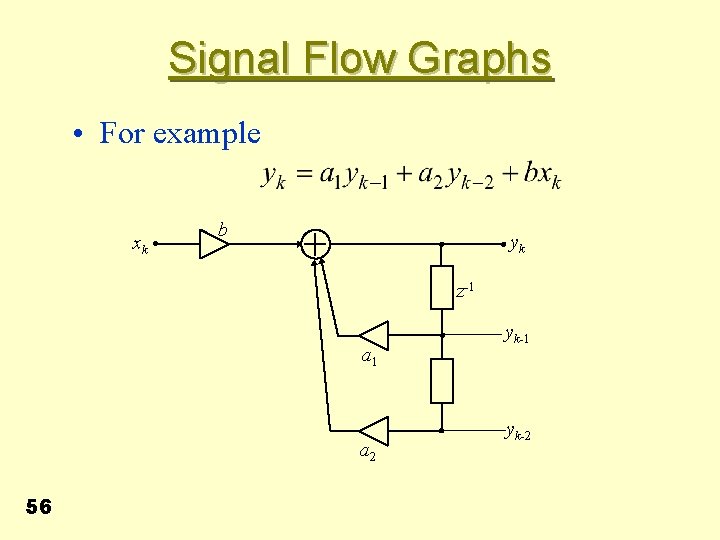
Signal Flow Graphs • For example xk b yk z-1 a 2 56 yk-1 yk-2

Signal Flow Graphs • A SFG structure indicates the way through which the operations are to be carried out in an implementation. • In a LTID system, a structure can be: i) computable : (All loops contain delays) ii) non-computable : (Some loops contain no delays) 57

Signal Flow Graphs • Transposition of SFG is the process of reversing the direction of flow on all transmission paths while keeping their transfer functions the same. • This entails: – Multipliers replaced by multipliers of same value – Adders replaced by branching points – Branching points replaced by adders • For a single-input / output SFG the transpose SFG has the same transfer function overall, as the original. 58

Structures • STRUCTURES: (The computational schemes for deriving the input / output relationships. ) • For a given transfer function there are many realisation structures. • Each structure has different properties w. r. t. • i) Coefficient sensitivity • ii) Finite register computations 59

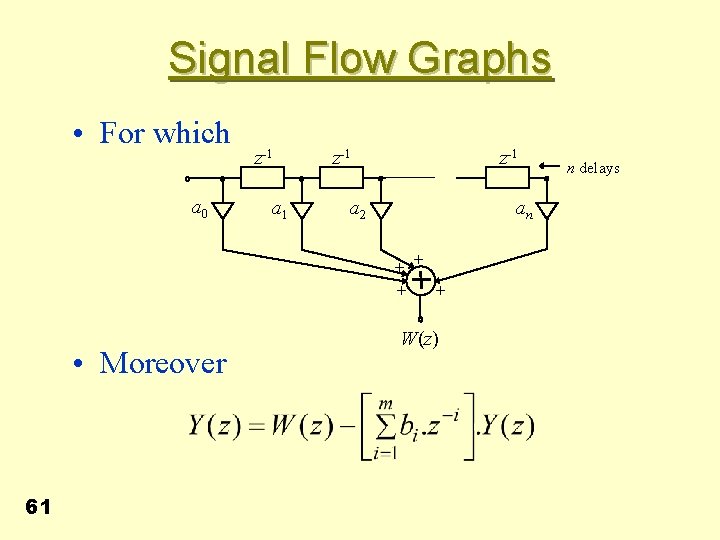
Signal Flow Graphs Direct form 1 : Consider the transfer function • So that • Set 60

Signal Flow Graphs • For which a 0 z-1 a 1 z-1 a 2 an + + • Moreover 61 W(z) n delays

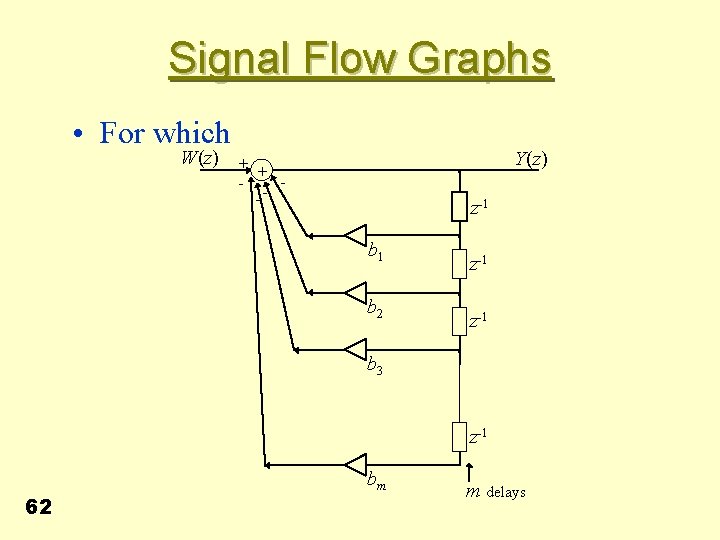
Signal Flow Graphs • For which W(z) Y(z) + + - z-1 b 2 z-1 b 3 z-1 62 bm m delays

Signal Flow Graphs • This figure and the previous one can be combined by cascading to produce overall structure. • Simple structure but NOT used extensively in practice because its performance degrades rapidly due to finite register computation effects 63

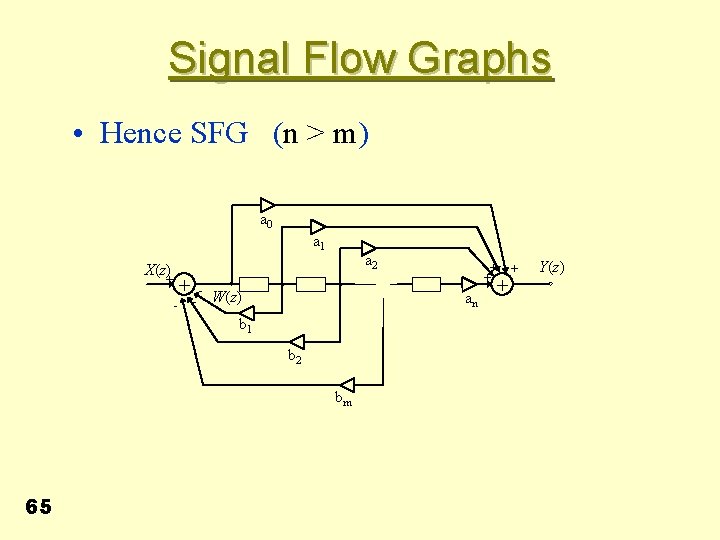
Signal Flow Graphs • Canonical form: Let • ie • and 64

Signal Flow Graphs • Hence SFG (n > m) a 0 a 1 X(z) + - - a 2 W(z) an b 1 b 2 bm 65 + + Y(z)

Signal Flow Graphs • Direct form 2 : Reduction in effects due to finite register can be achieved by factoring H(z) and cascading structures corresponding to factors • In general with • or 66

Signal Flow Graphs • Parallel form: Let • with Hi(z) as in cascade but a 0 i = 0 • With Transposition many more structures can be derived. Each will have different performance when implemented with finite precision 67

Signal Flow Graphs • Sensitivity: Consider the effect of changing a multiplier on the transfer function U(z) V(z) 2 1 X(z) 4 3 Y(z) Linear T-I Discrete System • Set 68 • With constraint

Signal Flow Graphs • Hence And thus 69

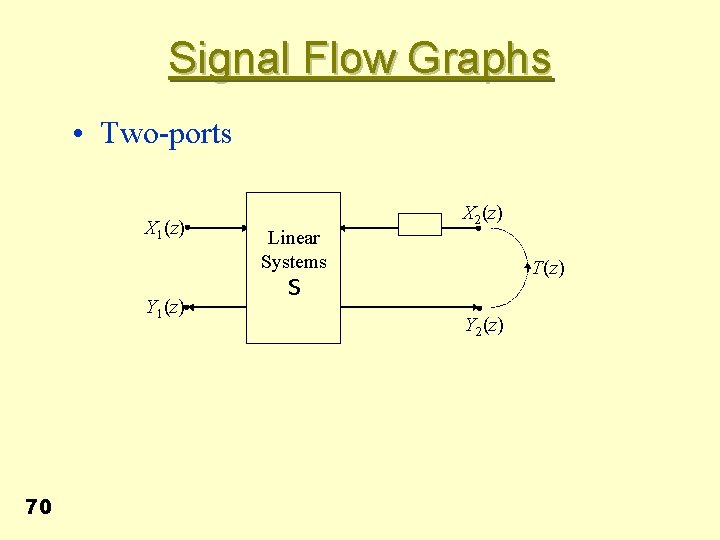
Signal Flow Graphs • Two-ports X 1(z) Y 1(z) 70 Linear Systems X 2(z) T(z) S Y 2(z)

Signal Flow Graphs • Example: Complex Multiplier x 1(n) y 1(n) M x 2(n) 71 y 2(n)

Signal Flow Graphs • So that • Its SFD can be drawn as x 1(n) x 2(n) 72 + + - + + + y 1(n) y 2(n)

Signal Flow Graphs • Special case • We have a rotation of t o by an angle • We can set so that and 73 • • This is the basis for designing i) Oscillators ii) Discrete Fourier Transforms (see later) iii) CORDIC operators in SONAR

Signal Flow Graphs • Example: Oscillator • Consider and externally impose the constraint So that • For oscillation 74

Signal Flow Graphs • Set • Hence 75

Signal Flow Graphs • With and , the oscillation frequency • Set then 76 and • We obtain • Hence x 1(n) and x 2(n) correspond to two sinusoidal oscillations at 90 w. r. t. each other

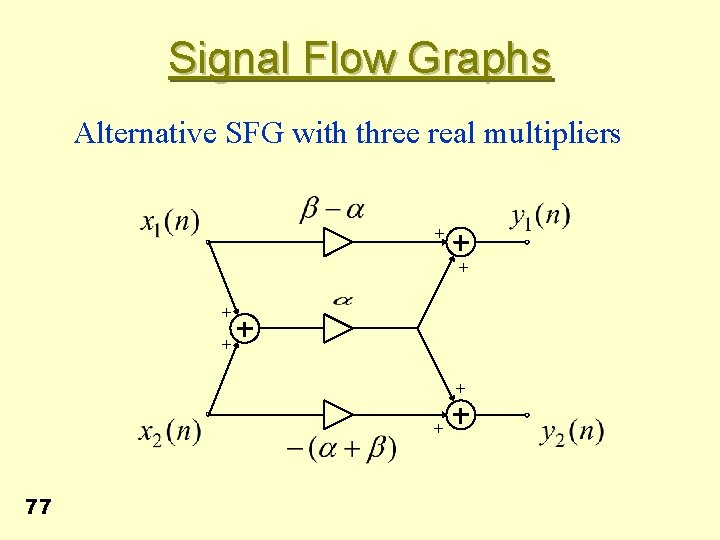
Signal Flow Graphs Alternative SFG with three real multipliers + + + 77

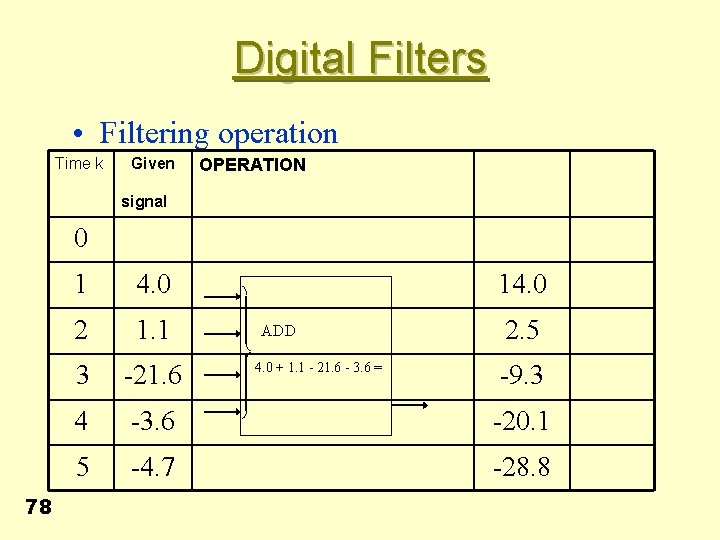
Digital Filters • Filtering operation Time k Given signal OPERATION 0 78 1 4. 0 14. 0 2 1. 1 3 -21. 6 4 -3. 6 -20. 1 5 -4. 7 -28. 8 ADD 4. 0 + 1. 1 - 21. 6 - 3. 6 = 2. 5 -9. 3

Digital Filters Filtering 79

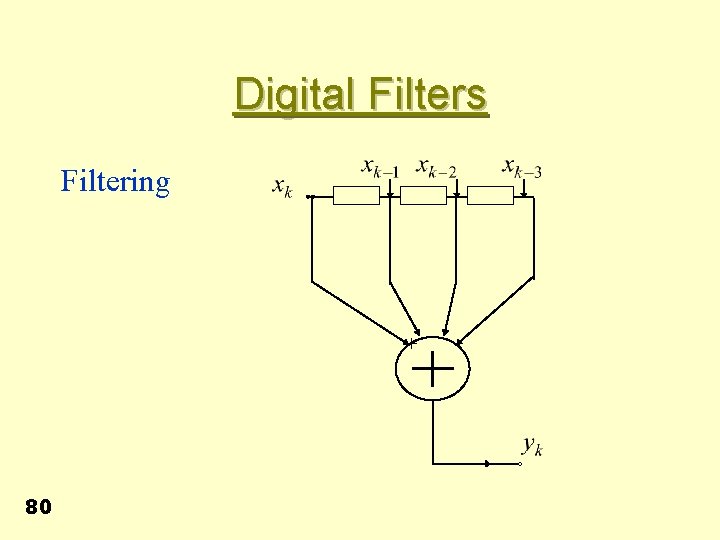
Digital Filters Filtering + 80 -

Digital Filters Filtering • Basic operations required • (a) Delay • (b) Addition • (c) Multiplication (Scaling) 81

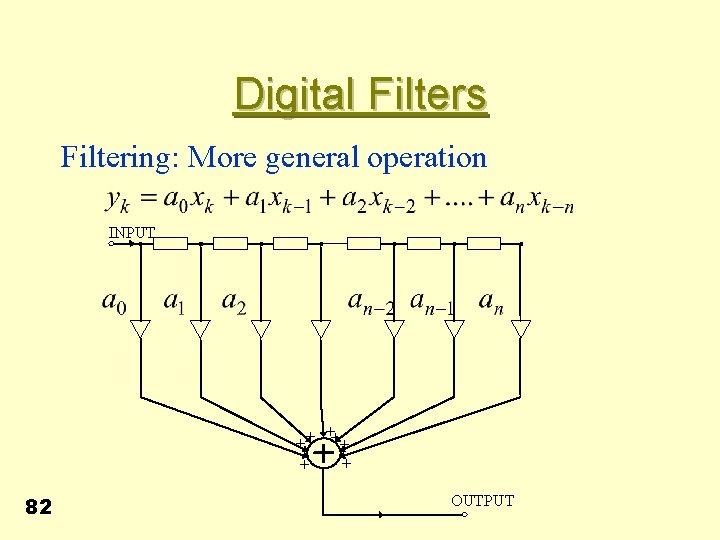
Digital Filters Filtering: More general operation INPUT + ++ + + 82 OUTPUT

Digital Filters Impulse response • Most general linear form • Recursive or Infinite Impulse Response (IIR) filters 83

Digital Filters A simple first order 84

Digital Filters Transfer function • For FIR 85

Digital Filters-Stability For IIR • Stability: Note that 86

Digital Filters Thus there is a pole at • if its magnitude is more than 1 then the impulse response increases without bound • if its magnitude is less than 1 decreases exponentially to zero • Frequency Response: Set and 87

Digital Filters So that • And hence • Compare with transfer function 88

Digital Filters In the initial example or • And thus 89

2 -D z tranform 2 -D z-transform • Example : 90

2 -D z tranform • And hence (i) (ii) 91 Separable transforms. Non-separable transforms.

2 -D Digital Filters 2 -D filters • Thus we can have • (a) FIR 2 -D filters and • (b) IIR 2 -D filters 92

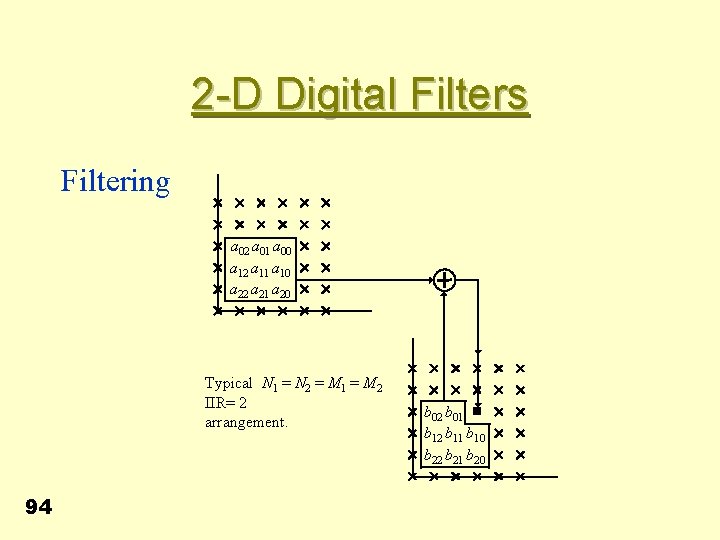
2 -D Digital Filters Transfer function • For convolution set 93

2 -D Digital Filters Filtering a 02 a 01 a 00 a 12 a 11 a 10 a 22 a 21 a 20 Typical N 1 = N 2 = M 1 = M 2 IIR= 2 arrangement. 94 b 02 b 01 b 12 b 11 b 10 b 22 b 21 b 20

2 -D Digital Filters (a) Separable filters (b) Non-separable filters is not expressible as a product of separate and independent factors 95

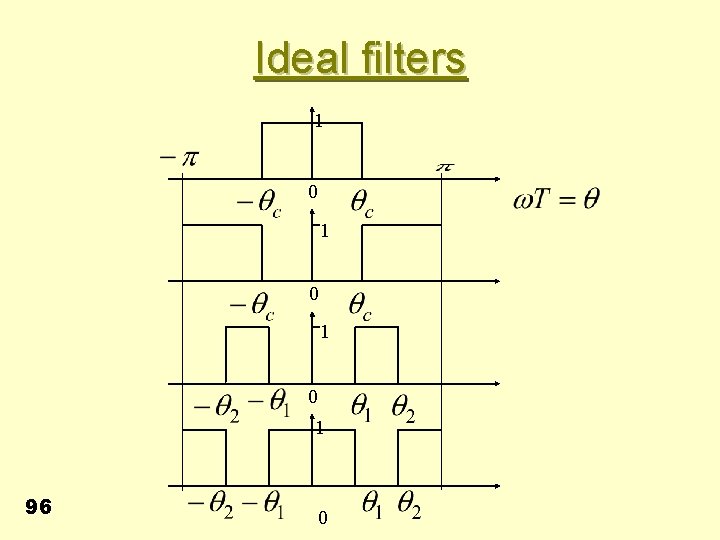
Ideal filters 1 0 1 0 1 96 0

Ideal filters 97