z Transform 10 When the transform is identical

z Transform (10) When the transform is identical to DFT (11)

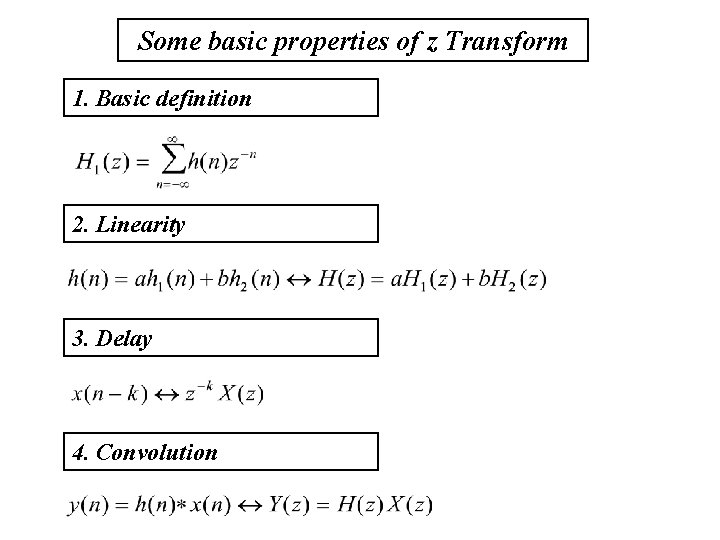
Some basic properties of z Transform 1. Basic definition 2. Linearity 3. Delay 4. Convolution

Essential properties of z Transform 5. Multiplication by ‘z-1’ 6. Relation between X(z) and X(-z) 7. Relation between X(z) and X(z-1)

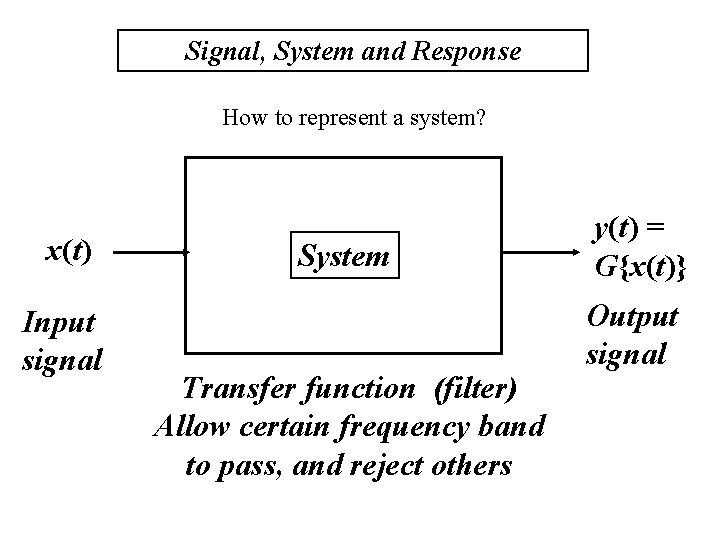
Signal, System and Response How to represent a system? x(t) Input signal System Transfer function (filter) Allow certain frequency band to pass, and reject others y(t) = G{x(t)} Output signal

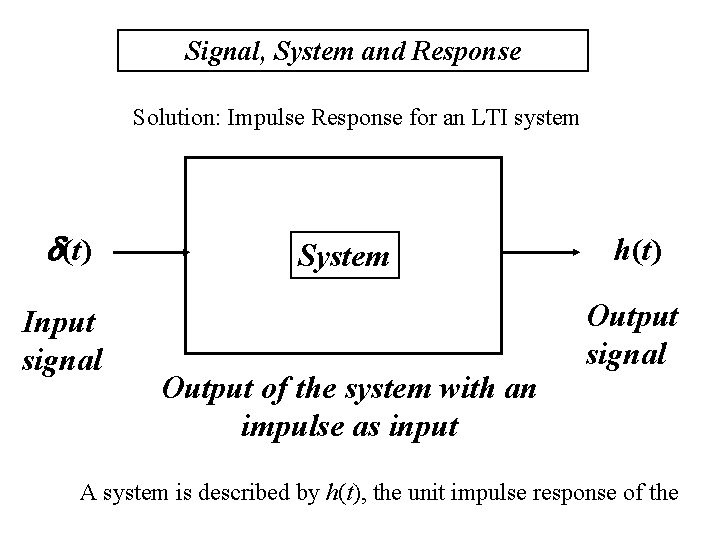
Signal, System and Response Solution: Impulse Response for an LTI system d(t) Input signal System Output of the system with an impulse as input h(t) Output signal A system is described by h(t), the unit impulse response of the

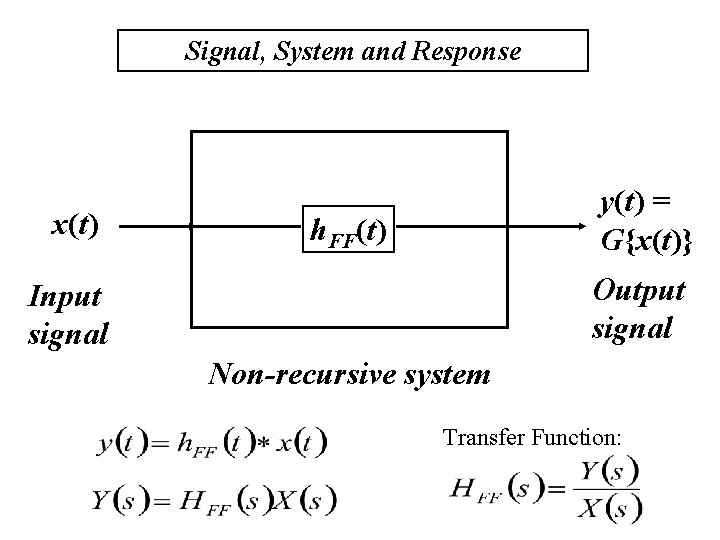
Signal, System and Response x(t) y(t) = G{x(t)} h. FF(t) Output signal Input signal Non-recursive system Transfer Function:

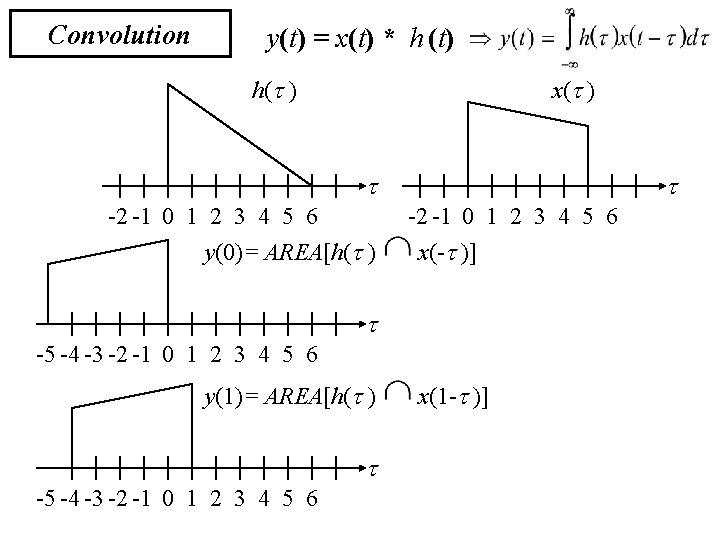
Convolution y(t) = x(t) * h (t) h( ) x( ) -2 -1 0 1 2 3 4 5 6 y(0)= AREA[h( ) -2 -1 0 1 2 3 4 5 6 x(- )] -5 -4 -3 -2 -1 0 1 2 3 4 5 6 y(1)= AREA[h( ) -5 -4 -3 -2 -1 0 1 2 3 4 5 6 x(1 - )]

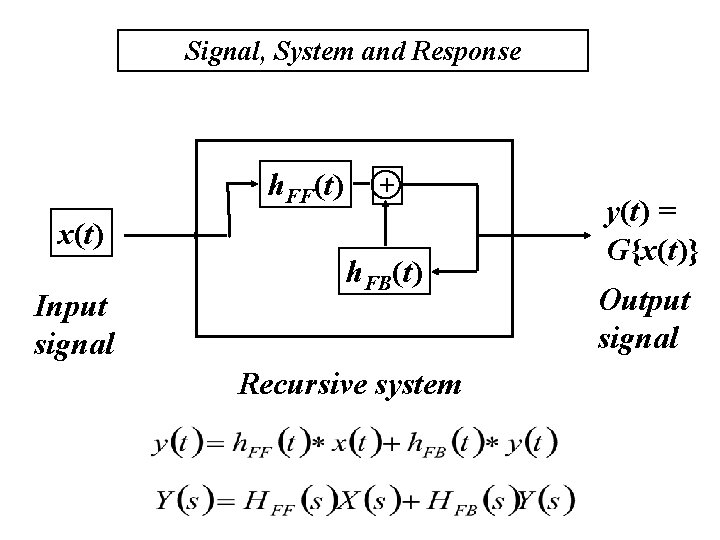
Signal, System and Response h. FF(t) + x(t) Input signal h. FB(t) Recursive system y(t) = G{x(t)} Output signal

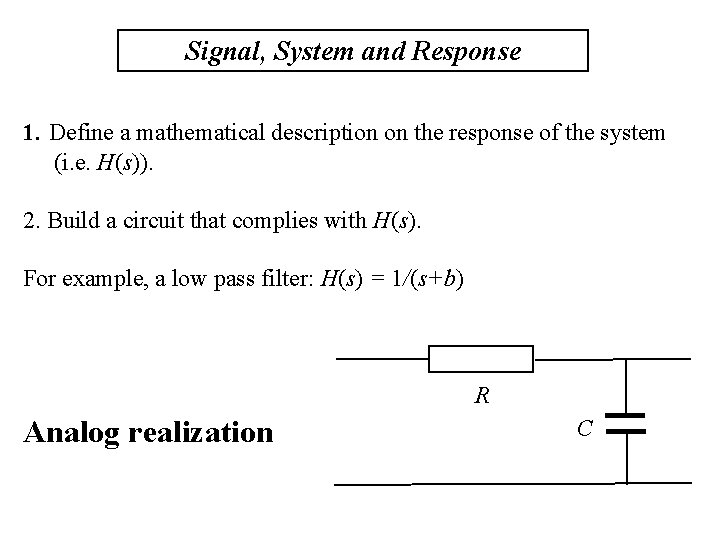
Signal, System and Response 1. Define a mathematical description on the response of the system (i. e. H(s)). 2. Build a circuit that complies with H(s). For example, a low pass filter: H(s) = 1/(s+b) R Analog realization C

Signal, System and Response Poles and Zeros Systems are defined by poles and zeros Design procedure of an analogue system 1. Given shape of frequency response 2. Determine H(s)

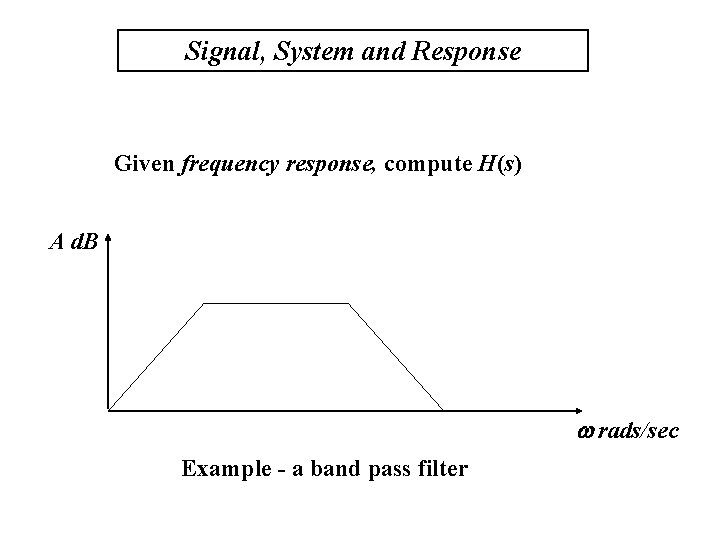
Signal, System and Response Given frequency response, compute H(s) A d. B w rads/sec Example - a band pass filter

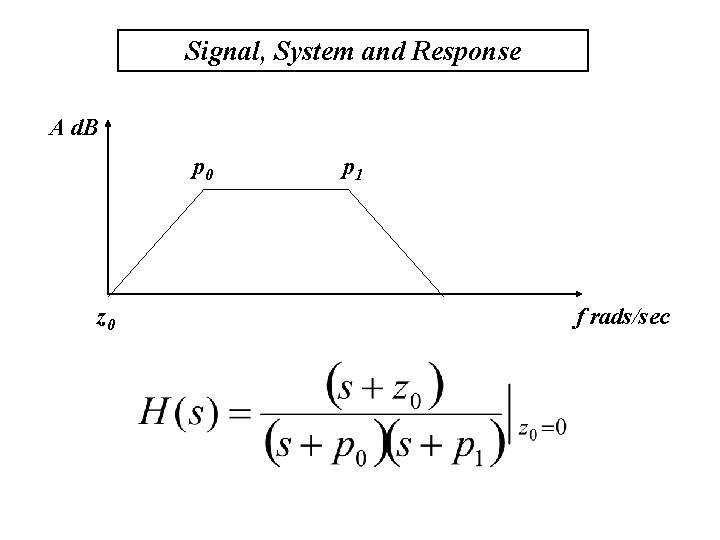
Signal, System and Response Compute H(s) from the frequency response : poles and zeros • Poles and zeros are frequencies • A pole indicate a drop of 20 d. B per decade • A zero indicate a gain of 20 d. B per decade • H(s) are formed by poles and zeros

Signal, System and Response A d. B p 0 z 0 p 1 f rads/sec

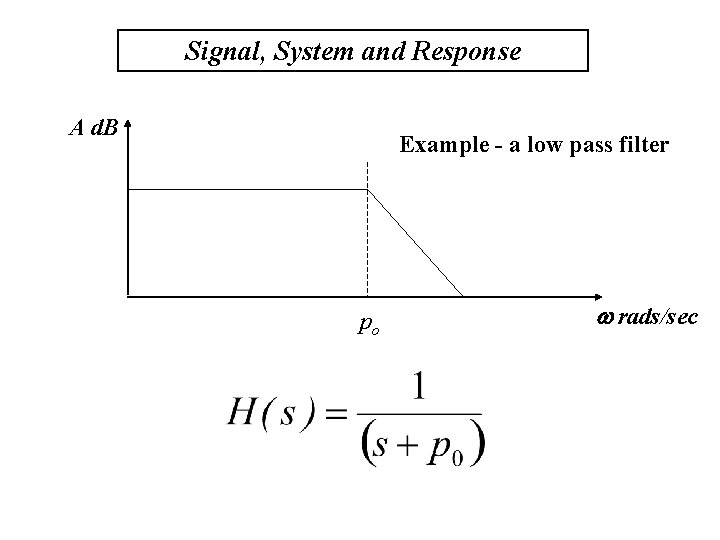
Signal, System and Response A d. B Example - a low pass filter po w rads/sec

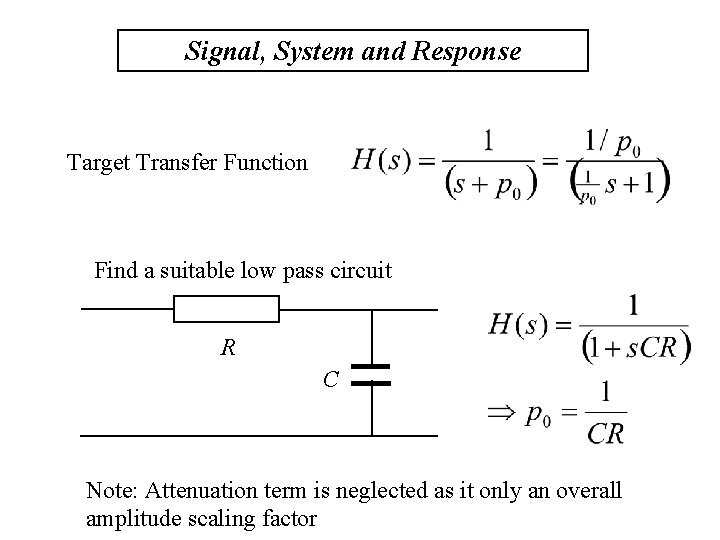
Signal, System and Response Target Transfer Function Find a suitable low pass circuit R C Note: Attenuation term is neglected as it only an overall amplitude scaling factor