Youngs double slit experiment Spatial coherence of light

Young’s double slit experiment & Spatial coherence of light Ivana Hamarová

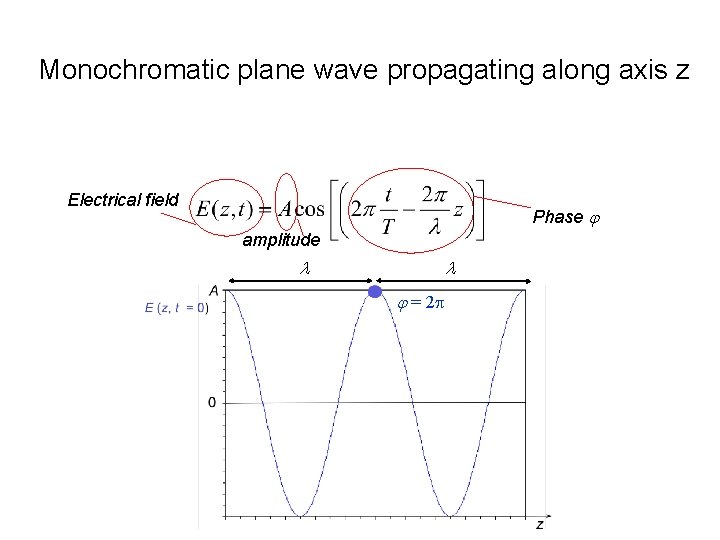
Monochromatic plane wave propagating along axis z Electrical field Phase j amplitude l l j = 2 p

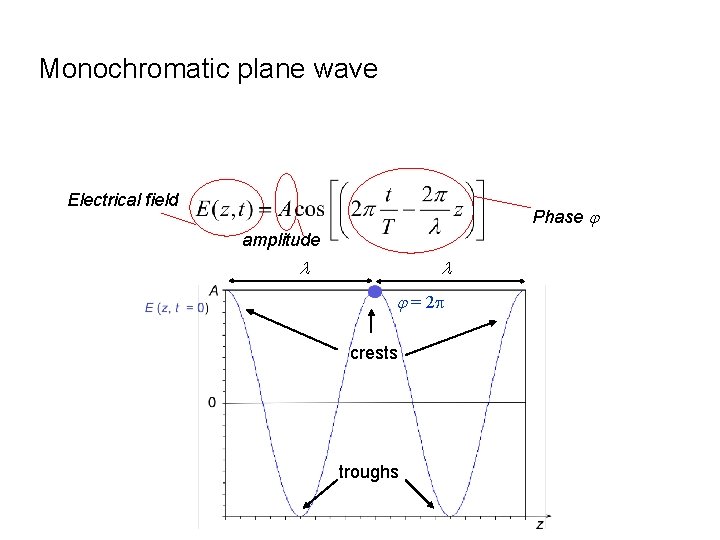
Monochromatic plane wave Electrical field Phase j amplitude l l j = 2 p crests troughs

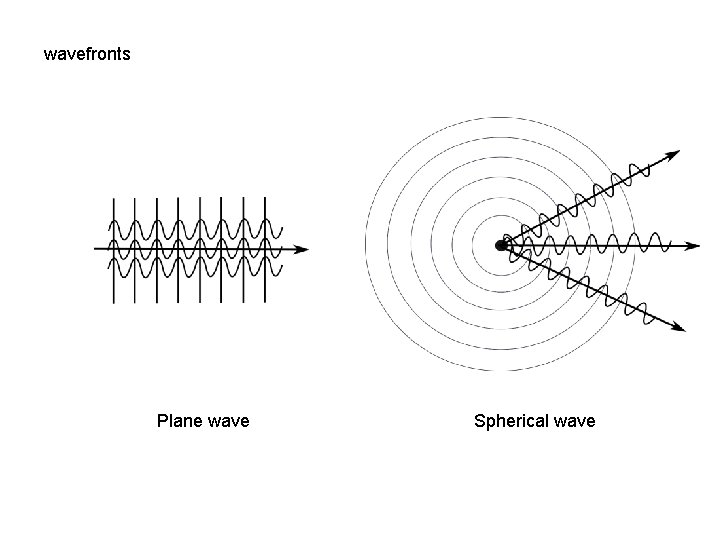
wavefronts Plane wave Spherical wave

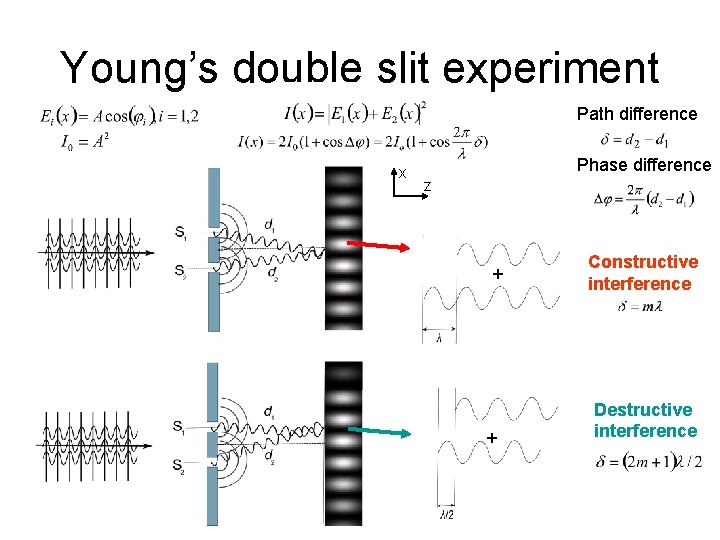
Young’s double slit experiment Path difference x Phase difference z + + Constructive interference Destructive interference

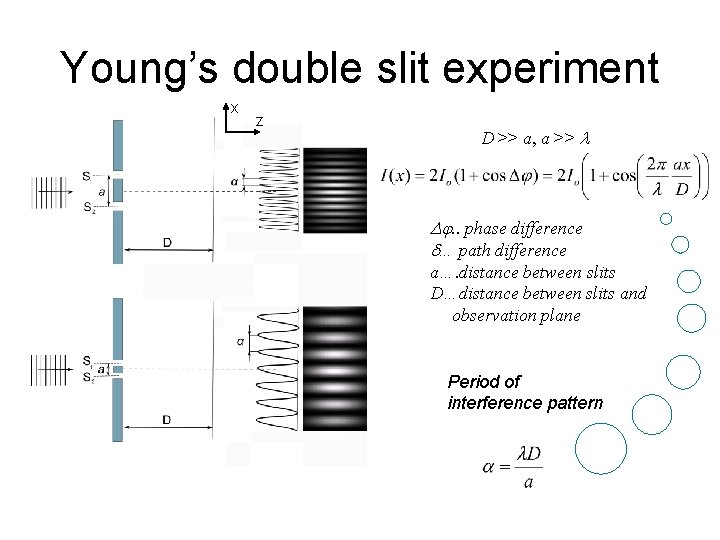
Young’s double slit experiment x z D >> a, a >> l Dj. . phase difference d… path difference a…. distance between slits D…distance between slits and observation plane Period of interference pattern

Effect of slit width on the interference pattern light block

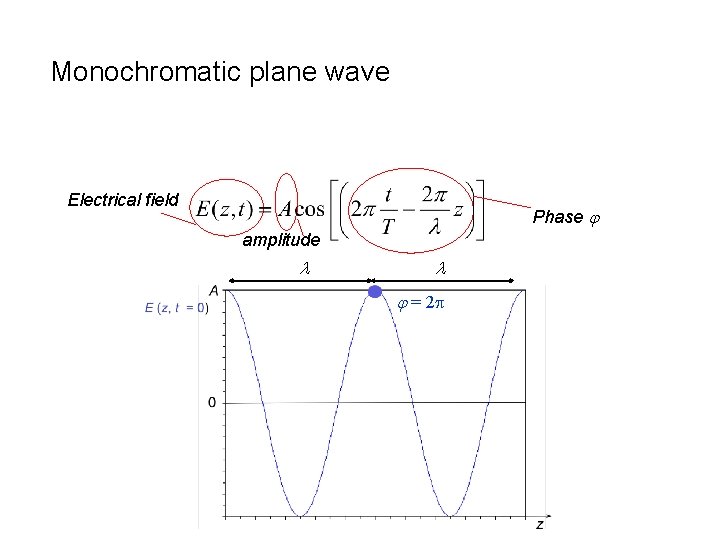
Monochromatic plane wave Electrical field Phase j amplitude l l j = 2 p

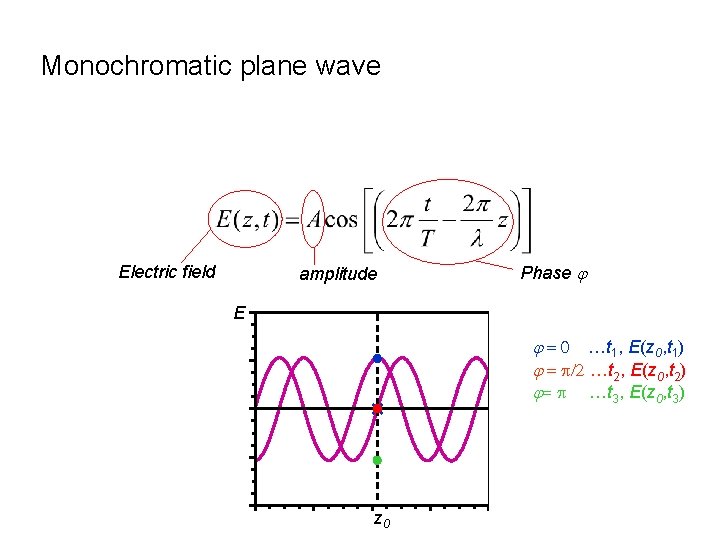
Monochromatic plane wave Electric field Phase j amplitude E j = 0 …t 1, E(z 0, t 1) j = p/2 …t 2, E(z 0, t 2) j= p …t 3, E(z 0, t 3) z 0 z

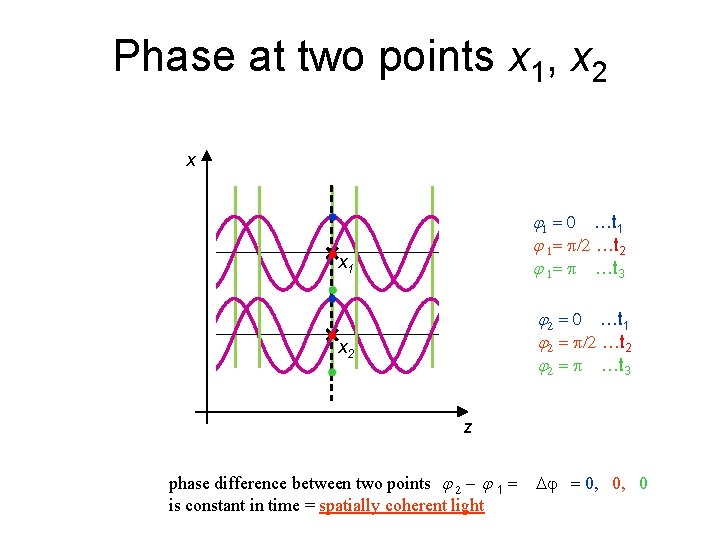
Phase at two points x 1, x 2 x j 1 = 0 …t 1 j 1= p/2 …t 2 j 1= p …t 3 x 1 j 2 = 0 …t 1 j 2 = p/2 …t 2 j 2 = p …t 3 x 2 z phase difference between two points j 2 - j 1 = is constant in time = spatially coherent light Dj = 0, 0, 0

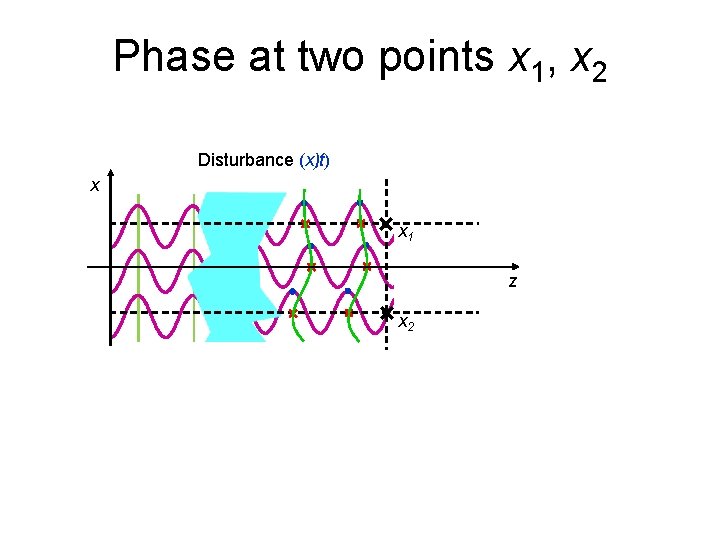
Phase at two points x 1, x 2 Disturbance (x) (x, t) x x 1 z x 2

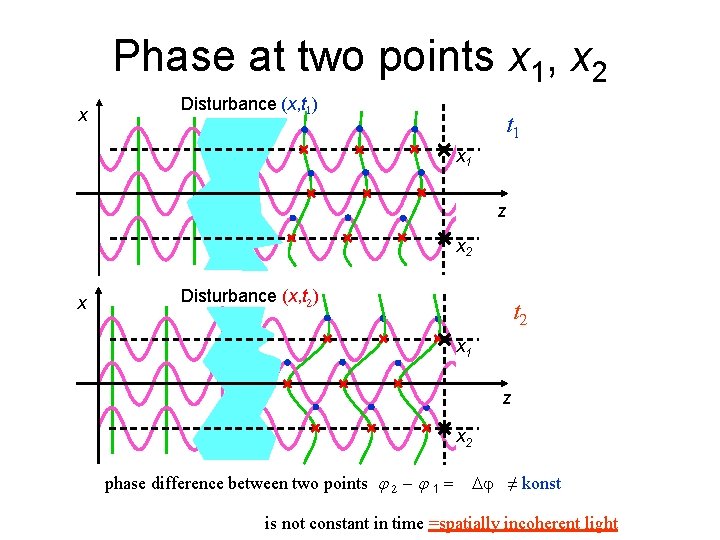
Phase at two points x 1, x 2 x Disturbance (x, t 1) t 1 x 1 z x 2 x Disturbance (x, t 2) t 2 x 1 z x 2 phase difference between two points j 2 - j 1 = Dj ≠ konst is not constant in time =spatially incoherent light

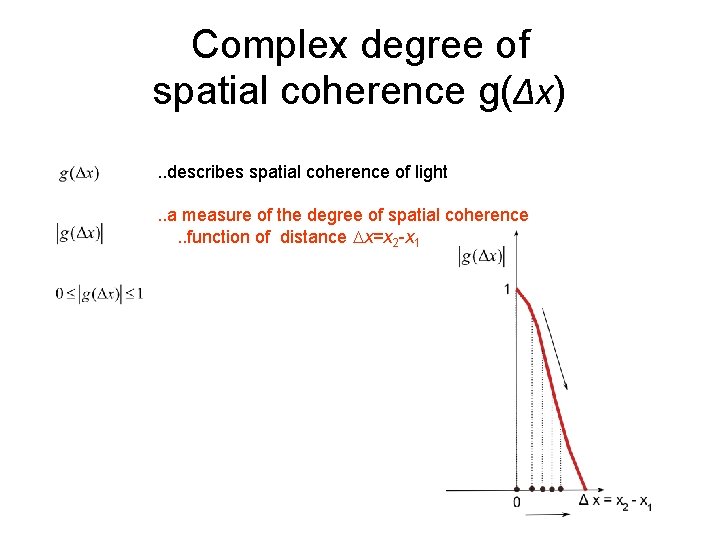
Complex degree of spatial coherence g(Δx). . describes spatial coherence of light. . a measure of the degree of spatial coherence. . function of distance Dx=x 2 -x 1

Spatial coherence of light x 1 1 Δx x 2 2

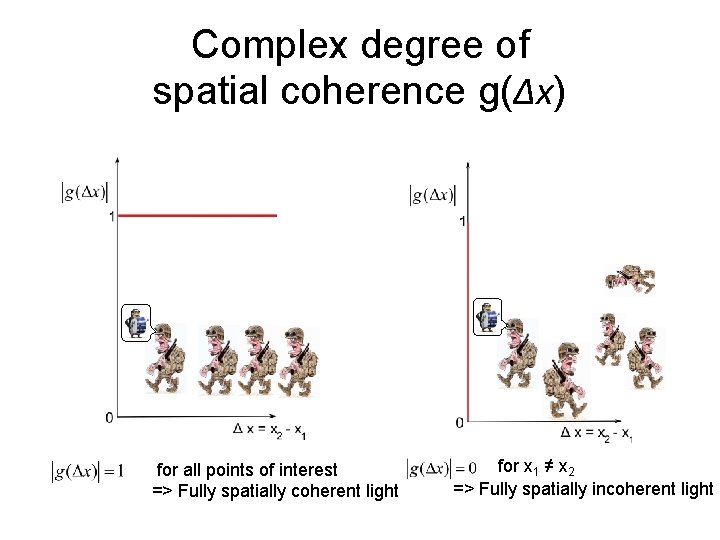
Complex degree of spatial coherence g(Δx) for all points of interest => Fully spatially coherent light for x 1 ≠ x 2 => Fully spatially incoherent light

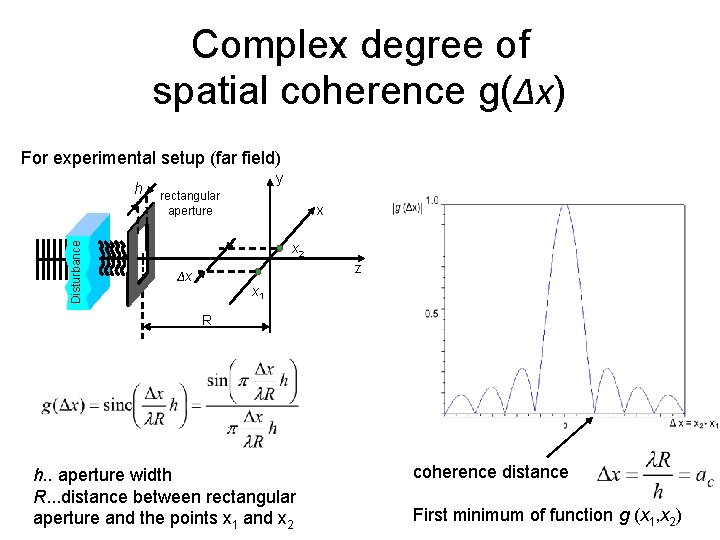
Complex degree of spatial coherence g(Δx) For experimental setup (far field) Disturbance h y rectangular aperture x x 2 z Δx x 1 R h. . aperture width R. . . distance between rectangular aperture and the points x 1 and x 2 coherence distance First minimum of function g (x 1, x 2)

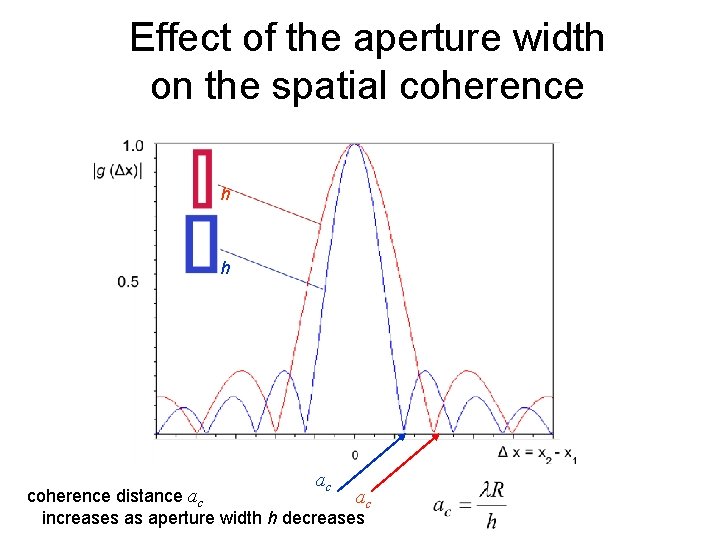
Effect of the aperture width on the spatial coherence h h ac coherence distance ac ac increases as aperture width h decreases

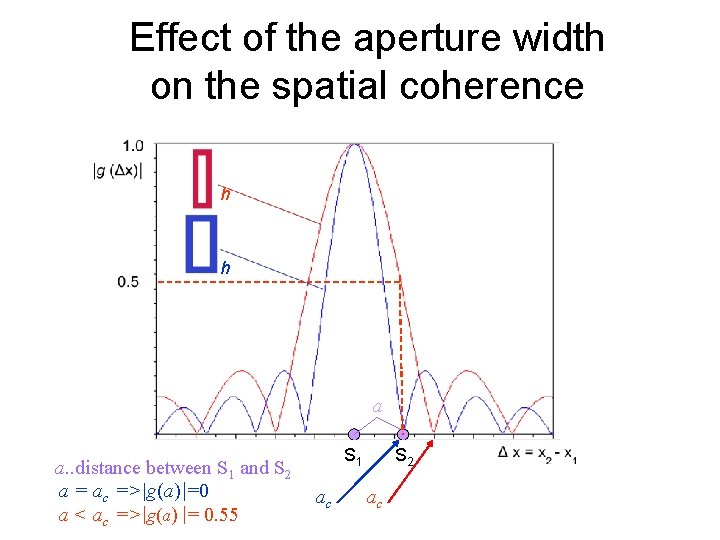
Effect of the aperture width on the spatial coherence h h a a. . distance between S 1 and S 2 a = ac => g(a) =0 a < ac => g(a) = 0. 55 S 1 ac S 2 ac

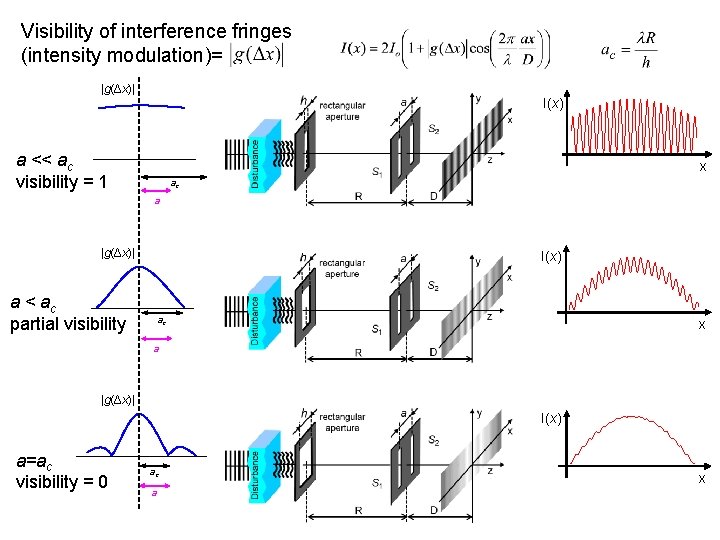
Visibility of interference fringes (intensity modulation)= |g(Δx)| I(x) a << ac visibility = 1 x ac a |g(Δx)| I(x) a < ac partial visibility ac x a |g(Δx)| I(x) a=ac visibility = 0 ac a x

Thank you for your attention