Yoan Lger Laboratory of Quantum Optoelectronics Ecole Polytechnique

Yoan Léger Laboratory of Quantum Opto-electronics Ecole Polytechnique Fédérale de Lausanne Switzerland POLARITON GAS EXCITATIONS: FROM SINGLE -PARTICLE TO SUPERFLUID

Polariton Superfluidity Heterodyne four wave mixing From standard fluid to superfluidity 2 d fourier spectroscopy

Superfluidity & sound wave excitations Striking properties of superfluids Zero viscosity, Rollin film, foutain effect Quantized vortices…. Bogoliubov theory of the weakly interacting Bose gas Elementary excitation are collective excitations! with sound wave behavior Woods et al. Rep. Prog. Phys. 36 1135 (1973)

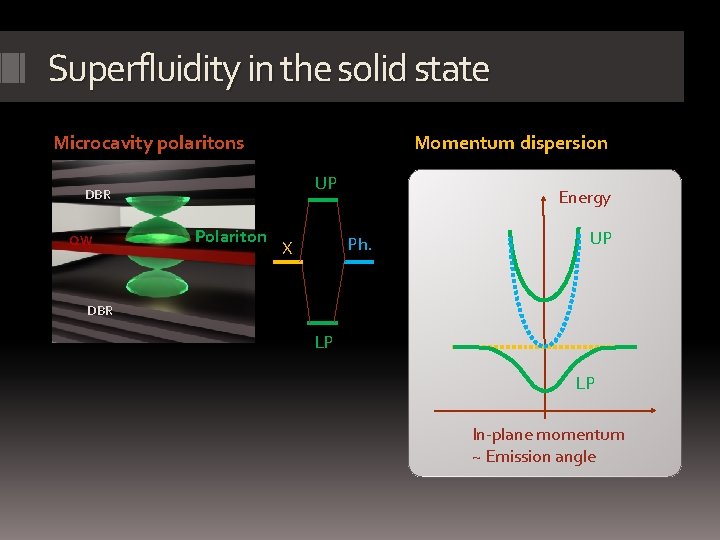
Superfluidity in the solid state Microcavity polaritons Momentum dispersion Cavity field DBR Polariton Exciton QW Spacing layer UP Energy Ph. X UP DBR LP LP In-plane momentum ~ Emission angle

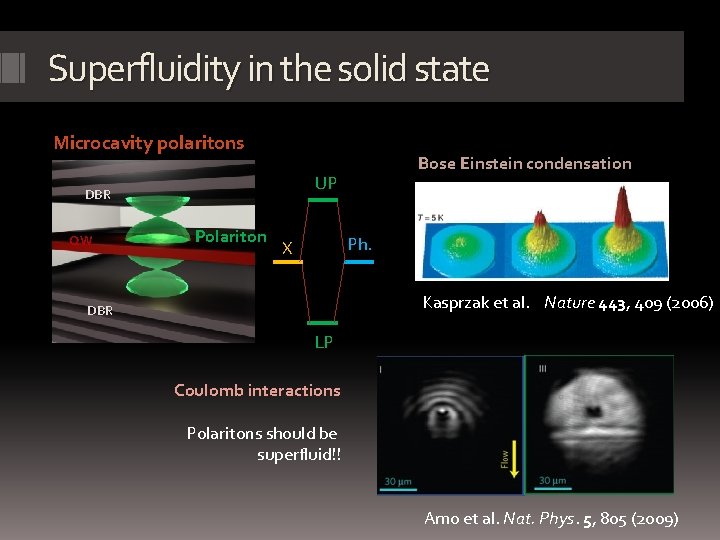
Superfluidity in the solid state Microcavity polaritons Cavity field DBR Polariton Exciton QW Spacing layer Bose Einstein condensation UP Ph. X Kasprzak et al. Nature 443, 409 (2006) DBR LP Coulomb interactions Polaritons should be superfluid!! Amo et al. Nat. Phys. 5, 805 (2009)

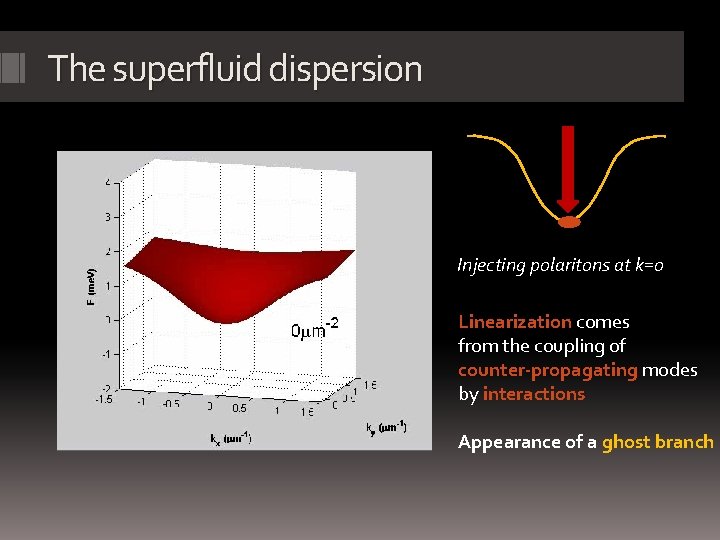
The superfluid dispersion Injecting polaritons at k=0 Linearization comes from the coupling of counter-propagating modes by interactions Appearance of a ghost branch

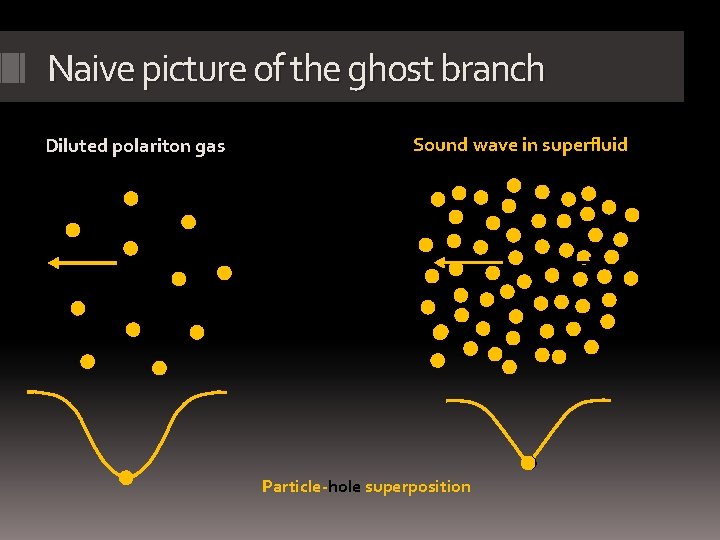
Naive picture of the ghost branch Diluted polariton gas Sound wave in superfluid Particle-hole superposition

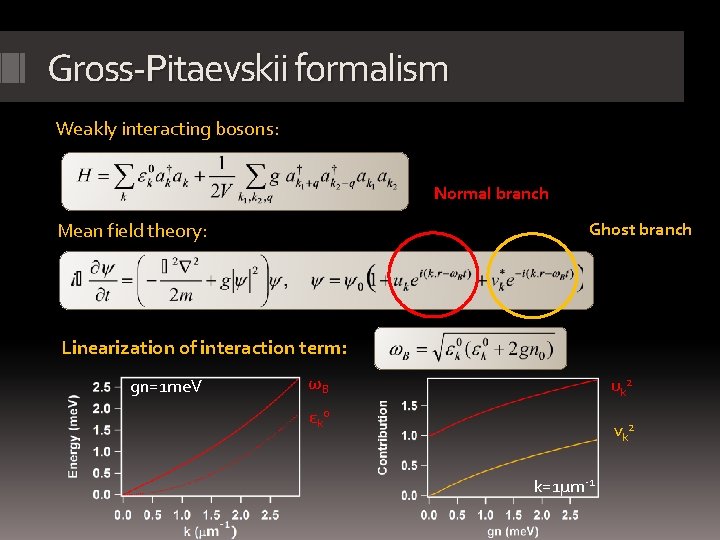
Gross-Pitaevskii formalism Weakly interacting bosons: Normal branch Ghost branch Mean field theory: Linearization of interaction term: gn=1 me. V ωB uk 2 εk 0 vk 2 k=1μm-1

Looking for the Ghost branch PL measurements Kind of linearization No ghost branch Utsunomiya et al. Nat. Phys. 4, 700 (2008) Accessing the ghost branch with FWM In the proposal: non-resonant condensate Wouters et al. Phys. Rev. B 79, 125311 (2009)

Polariton Superfluidity Heterodyne four wave mixing From standard fluid to superfluidity 2 d fourier spectroscopy

Polariton FWM Four wave mixing and selection rules Third order nonlinearity Angular selection rule Energy selection rule

Polariton FWM Four wave mixing and selection rules Third order nonlinearity Angular selection rule Energy selection rule Polariton FWM 2 fields : condensate field and probe field Stimulated parametric scattering of 2 polaritons from the condensate

Heterodyne FWM Problem: Condensate emission should largely dominate the spectrum How to extract useful signal when angular selection is not enough? Heterodyne FWM • Based on spectral interferometry Excitation fields Linear emission FWM Heterodyne setup • requires : • a full control of the excitation fields • Pulsed excitation to cover the full emission spectrum • provides: • best sensitivity, and selectivity • access to amplitude and phase of the nonlinear emission FWM

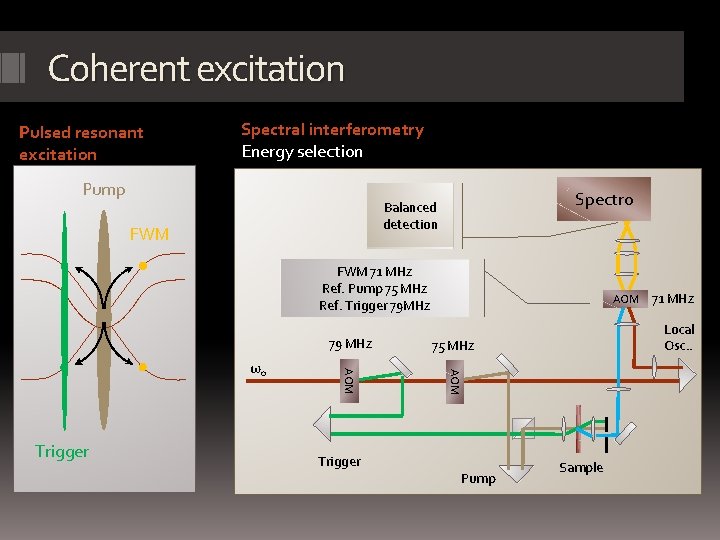
Coherent excitation Pulsed resonant excitation Spectral interferometry Energy selection Pump Spectro Balanced detection FWM 71 MHz Ref. Pump 75 MHz Ref. Trigger 79 MHz 75 MHz AOM Trigger 79 MHz AOM ω0 AOM Trigger Pump 71 MHz Local Osc. . Sample

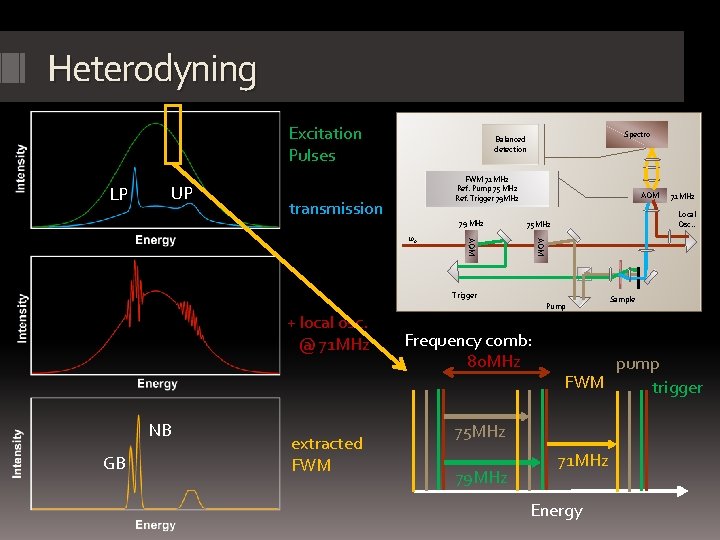
Heterodyning Excitation Pulses LP UP Spectro Balanced detection FWM 71 MHz Ref. Pump 75 MHz Ref. Trigger 79 MHz 75 MHz AOM ω0 79 MHz AOM transmission AOM Local Osc. . Trigger Pump + local osc. @ 71 MHz NB GB extracted FWM Frequency comb: 80 MHz Sample pump FWM trigger 75 MHz 79 MHz 71 MHz Energy

Polariton Superfluidity Heterodyne four wave mixing From standard fluid to superfluidity 2 d fourier spectroscopy

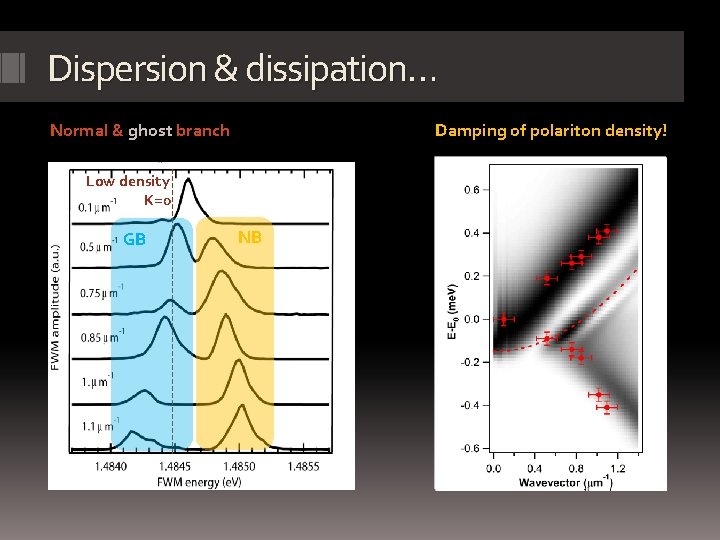
Dispersion & dissipation… Normal & ghost branch Damping of polariton density! Low density K=0 GB t 1 NB t 2 t 3

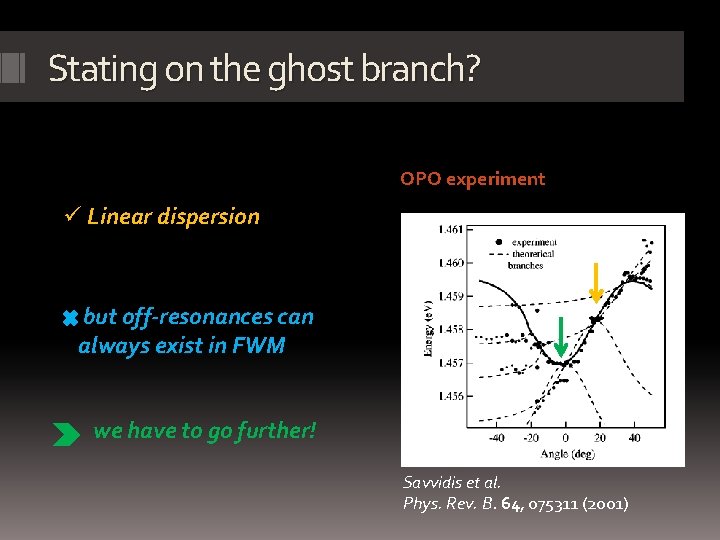
Stating on the ghost branch? OPO experiment ü Linear dispersion but off-resonances can always exist in FWM we have to go further! Savvidis et al. Phys. Rev. B. 64, 075311 (2001)

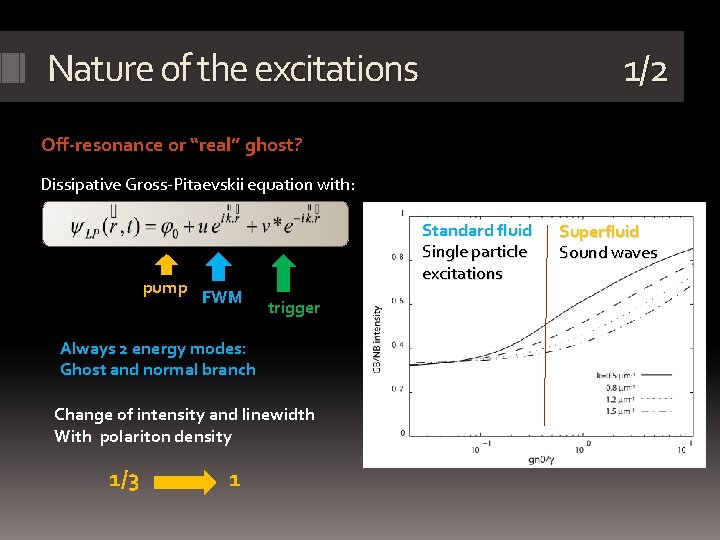
Nature of the excitations 1/2 Off-resonance or “real” ghost? Dissipative Gross-Pitaevskii equation with: pump Standard fluid Single particle excitations FWM trigger Always 2 energy modes: Ghost and normal branch Change of intensity and linewidth With polariton density 1/3 1 Superfluid Sound waves

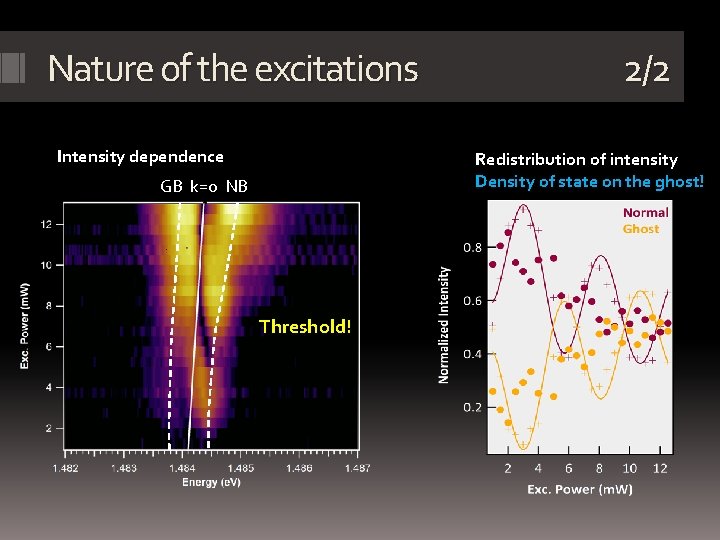
Nature of the excitations Intensity dependence 2/2 Redistribution of intensity Density of state on the ghost! GB k=0 NB Threshold!

Polariton Superfluidity Heterodyne four wave mixing From standard fluid to superfluidity 2 d fourier spectroscopy

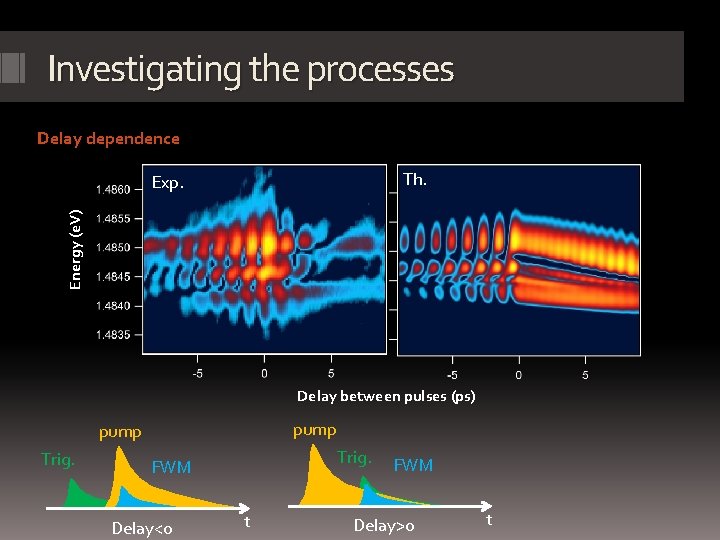
Investigating the processes Delay dependence Th. Energy (e. V) Exp. Delay between pulses (ps) pump Trig. FWM Delay<0 t FWM Delay>0 t

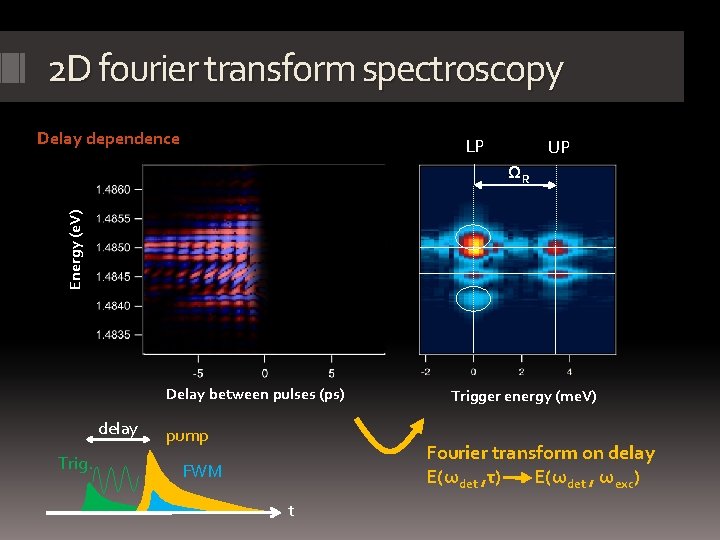
2 D fourier transform spectroscopy Delay dependence LP UP Energy (e. V) ΩR Delay between pulses (ps) delay Trig. pump Trigger energy (me. V) Fourier transform on delay E(ωdet , τ) E(ωdet , ωexc) FWM t

Conclusions & perspectives Ghost branch of a superfluid • In solid state, for the first time • Transformation of the excitations Sound like dispersion • Linear for the normal branch • Assymmetry due to dissipation 2 D fourier transform spectroscopy • Highly powerful method • Starting the process investigation…

acknowledgements To the audience! To my collaborators: Verena Kohnle, Michiel Wouters, Maxime Richard, Marcia Portella-Oberli, Benoit Deveaud-Plédran