Yet another approach to the To Fbased PID

Yet another approach to the To. F-based PID at PANDA A. Kiselev, Yu. Naryshkin PANDA Collaboration Meeting Stockholm, 14. 06. 2010

Layout of the talk n Motivation of this work Suggested formalism Monte-Carlo results n Discussion n n

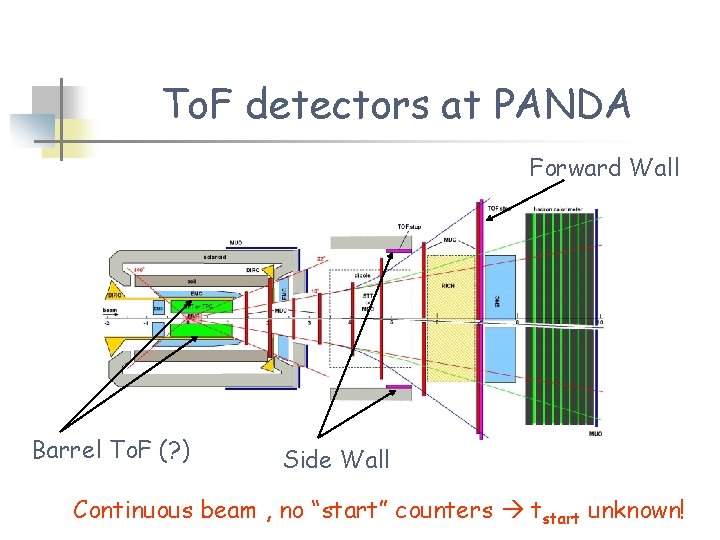
To. F detectors at PANDA Forward Wall Barrel To. F (? ) Side Wall Continuous beam , no “start” counters tstart unknown!

Algorithms considered so far Three main procedures: Ø Reconstruction from one identified particle Ø Minimization mass residuals under start time variations Ø Mass hypothesis find time offset The following 3 slides: Stefano Spataro, Sep’ 2008

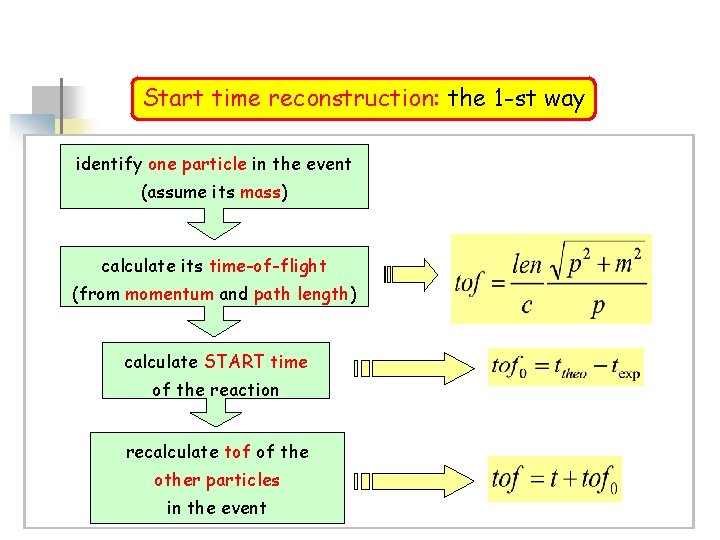
Start time reconstruction: the 1 -st way identify one particle in the event (assume its mass) calculate its time-of-flight (from momentum and path length) calculate START time of the reaction recalculate tof of the other particles in the event

Start time reconstruction: the 2 nd way New algorithm was implemented (Alexander Schmah) Ø variation of start time tstart Ø calculate mass from tstart, momentum, tof, path length Ø find the closest realistic mass Ø construct residual for all the particles Find tstart that minimizes the Q functional

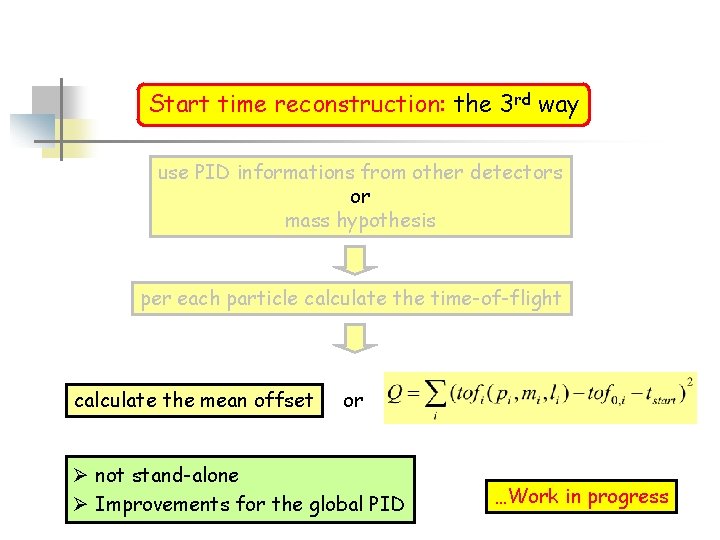
Start time reconstruction: the 3 rd way use PID informations from other detectors or mass hypothesis per each particle calculate the time-of-flight calculate the mean offset or Ø not stand-alone Ø Improvements for the global PID …Work in progress

The “ 4 -th way”: goals n Quantify PID decision as much as possible Provide statistically significant formulation Have a better interface to tracking package n Be flexible in terms of input: n n do not require ANY external PID info per default be able to use such information, if available n Allow flexible output: be able either to provide its own PID decision … … or, alternatively, give input for the “global” PID

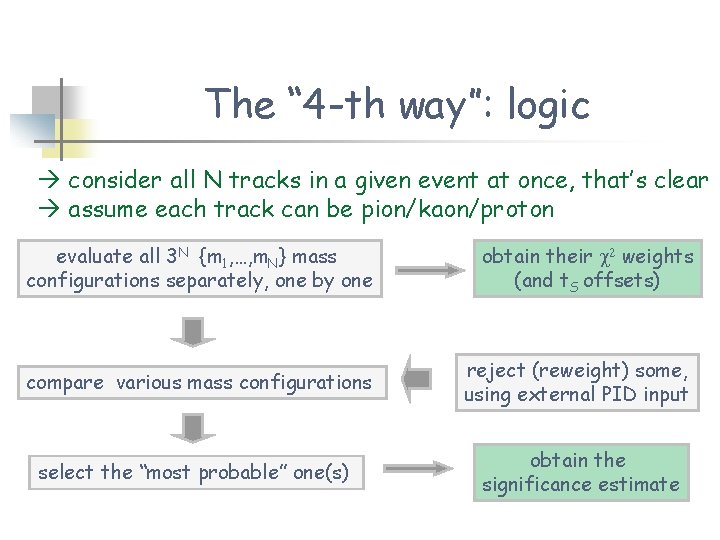
The “ 4 -th way”: logic consider all N tracks in a given event at once, that’s clear assume each track can be pion/kaon/proton evaluate all 3 N {m 1, …, m. N} mass configurations separately, one by one obtain their c 2 weights (and t. S offsets) compare various mass configurations reject (reweight) some, using external PID input select the “most probable” one(s) obtain the significance estimate

Formalism (simplified version) how to evaluate a given {m 1, …, m. N} mass configuration? n n Y (t. S 0) is distributed as c 2 with N-1 degrees of freedom for “correct” mass configurations Tends to have higher c 2 values for the “wrong” ones

Standalone PID evaluation calculate “weight” for each {m 1, …, m. N} configuration: define “probability” of j-th track to be say a pion as use Monte-Carlo to check selection efficiency & proton contamination (in this report: PYTHIA @10 Ge. V/c, forward spectrometer tracks only)

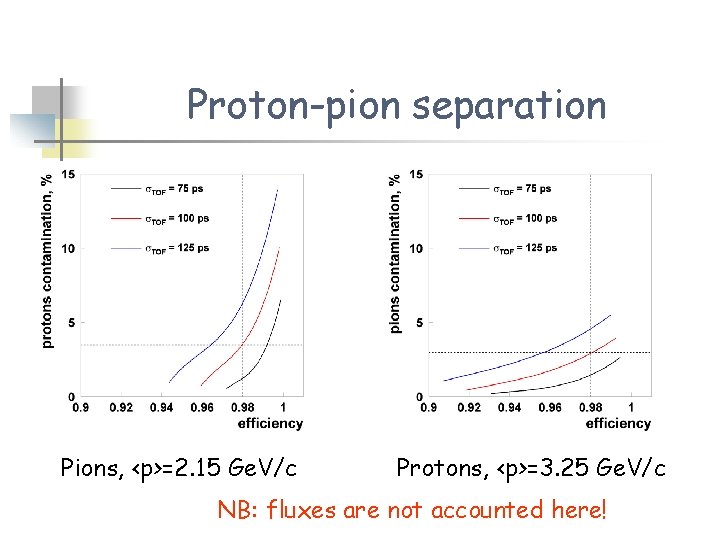
Proton-pion separation Pions, <p>=2. 15 Ge. V/c Protons, <p>=3. 25 Ge. V/c NB: fluxes are not accounted here!

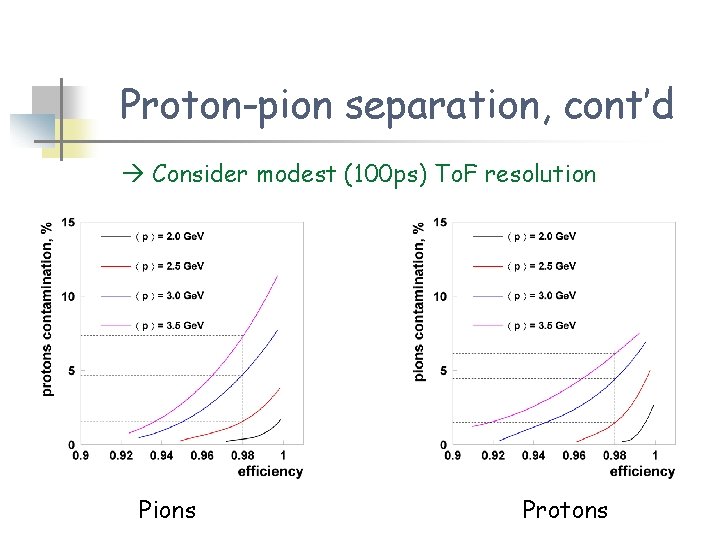
Proton-pion separation, cont’d Consider modest (100 ps) To. F resolution Pions Protons

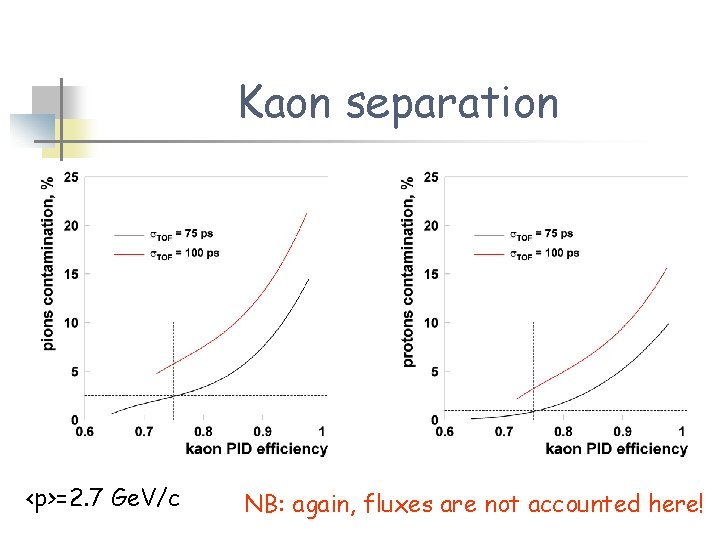
Kaon separation <p>=2. 7 Ge. V/c NB: again, fluxes are not accounted here!

Formalism (advanced version) n Extra requirements to the tracking package: n n append {t. S} to the “standard” Kalman filter {x, y, sx, sy, 1/p} parameter set do track fitting for pion/kaon/proton hypotheses separately provide {p, l, t. S}i parameter set with cov. matrix on per-track (and per-mass-hypothesis) basis This allows to extend the suggested formalism in a way, that To. F-based PID 1) is not biased by unknown t. S offsets during the 1 -st tracking pass, 2) gives the most complete and statistically meaningful set of information to the “global” PANDA PID code

Formalism (advanced, in detail) Kalman filter c 2 Track->event To. F matching measurement extended parameter set requires further studies!

Summary n n The (relatively) new formalism to handle PANDA To. F-based PID problem is suggested It allows to implement a statistically solid interface between tracking code, To. F measurements and the “global” PID