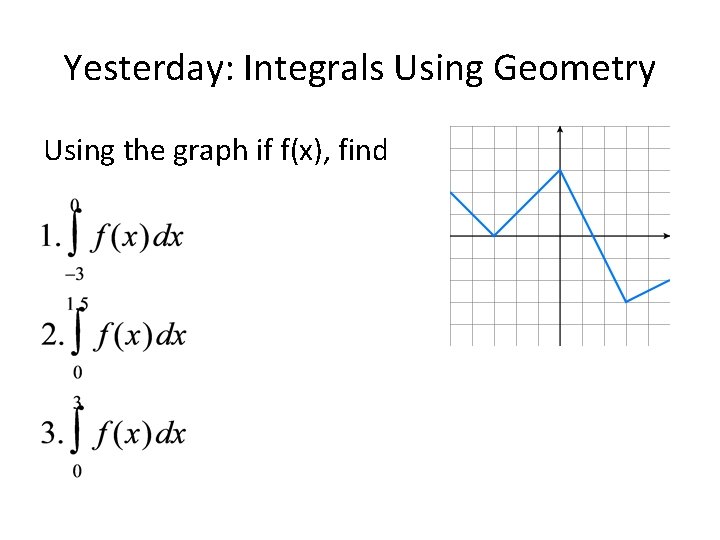
Yesterday Integrals Using Geometry Using the graph if

AP Calculus Unit 5 Day 2 Area Under a Curve Approximately (3 Day topic)

Riemann Sums • Riemann sums use rectangles to approximate area under curves LRAM RRAM

Rectangular Approximation Method (RAM) to estimate area under curve Example Problem: Use LRAM with

Rectangular Approximation Method (RAM) to estimate area under curve SOLUTION Example Problem: Use LRAM

Is this an overestimate or an underestimate? What if the function had been a

SOLUTION (1)(1)+(4)(1)+(9)(1)=14 Is this an overestimate or an underestimate? What if the function had

BEWARE—MRAM uses the average of the two x-values NOT the two y-values! MRAM gives

Midpoint Method Solution Find the area between the x-axis and y = x 2

Complete the following table: Increasing Function LRAM RRAM Decreasing Function

Under/Over Estimates for Increasing Function LRAM produces an _______ underestimate RRAM produces an _______

Under/Over Estimates for Decreasing Function LRAM produces an _______ overestimate RRAM produces an _______

How do we get the best underestimate of the area between a and b?

Slides: 15

Download presentation

Yesterday: Integrals Using Geometry Using the graph if f(x), find

AP Calculus Unit 5 Day 2 Area Under a Curve Approximately (3 Day topic)

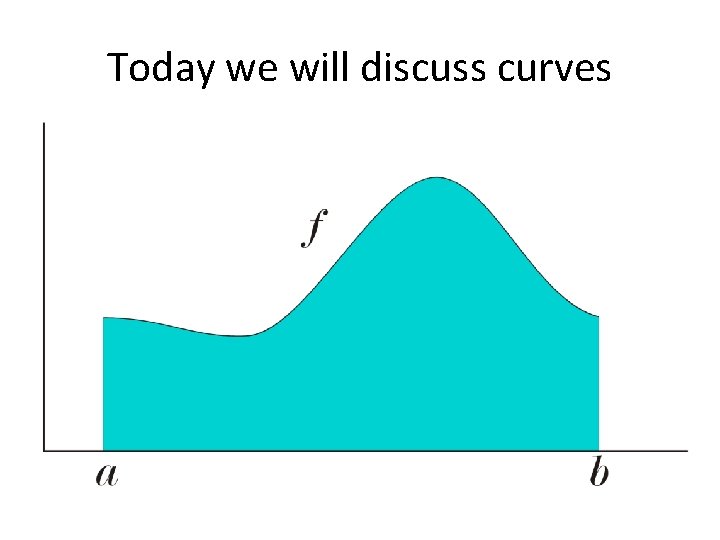
Today we will discuss curves

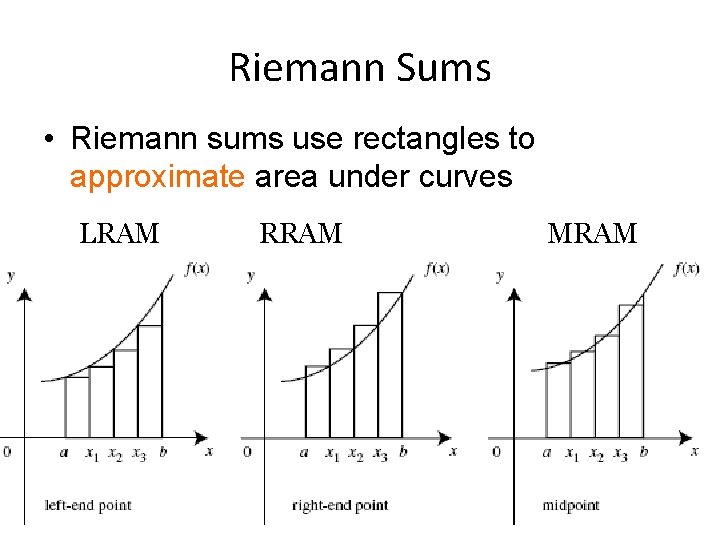
Riemann Sums • Riemann sums use rectangles to approximate area under curves LRAM RRAM MRAM

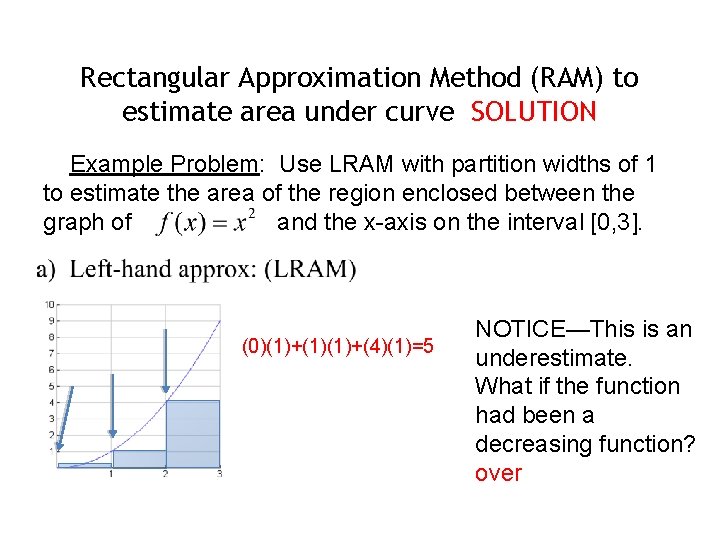
Rectangular Approximation Method (RAM) to estimate area under curve Example Problem: Use LRAM with partition widths of 1 to estimate NOTICE—This is an underestimate. What if the function had been a decreasing function?

Rectangular Approximation Method (RAM) to estimate area under curve SOLUTION Example Problem: Use LRAM with partition widths of 1 to estimate the area of the region enclosed between the graph of and the x-axis on the interval [0, 3]. (0)(1)+(1)(1)+(4)(1)=5 NOTICE—This is an underestimate. What if the function had been a decreasing function? over

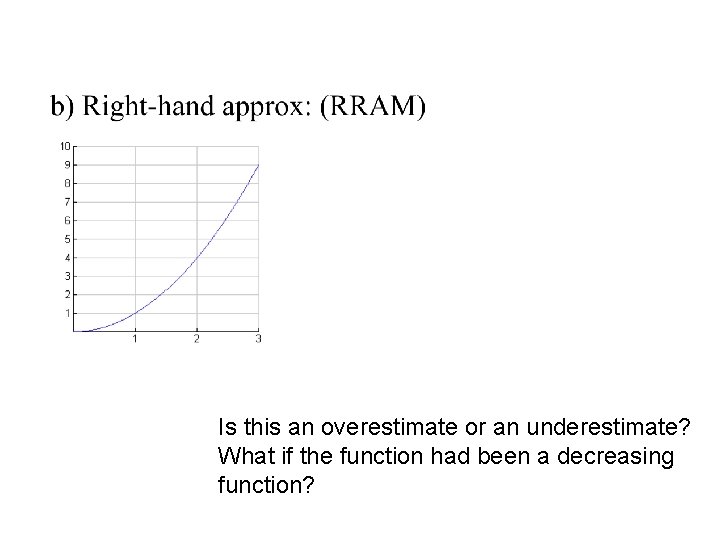
Is this an overestimate or an underestimate? What if the function had been a decreasing function?

SOLUTION (1)(1)+(4)(1)+(9)(1)=14 Is this an overestimate or an underestimate? What if the function had been a decreasing function? Under

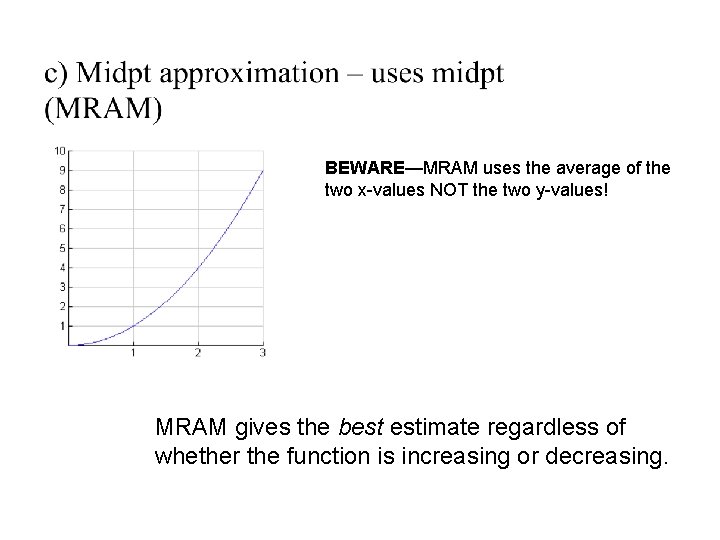
BEWARE—MRAM uses the average of the two x-values NOT the two y-values! MRAM gives the best estimate regardless of whether the function is increasing or decreasing.

Midpoint Method Solution Find the area between the x-axis and y = x 2 between [0, 3] with partition widths of 1. MRAM: The Midpoint of each rectangle touches the graph. The middle x-values in each region

CAUTION!!!! MRAM ≠ (LRAM + RRAM)/2

Complete the following table: Increasing Function LRAM RRAM Decreasing Function

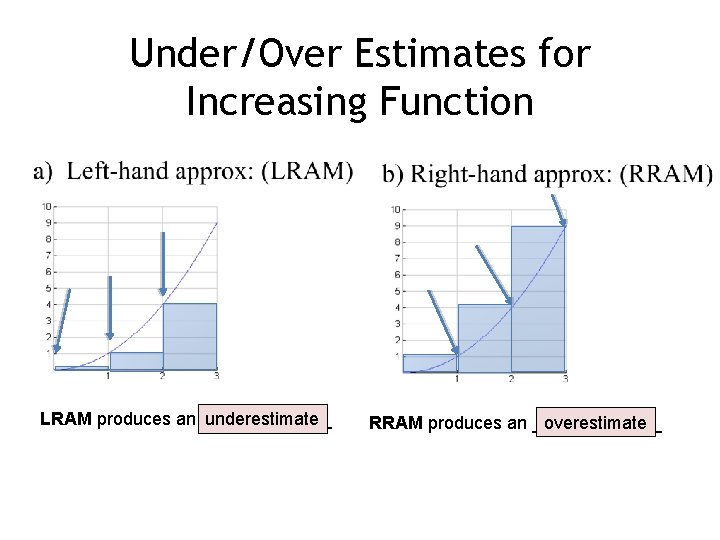
Under/Over Estimates for Increasing Function LRAM produces an _______ underestimate RRAM produces an _______ overestimate

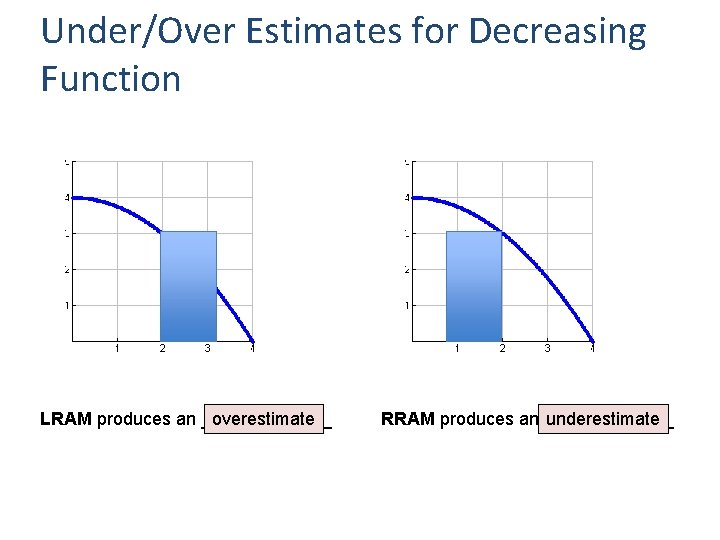
Under/Over Estimates for Decreasing Function LRAM produces an _______ overestimate RRAM produces an _______ underestimate

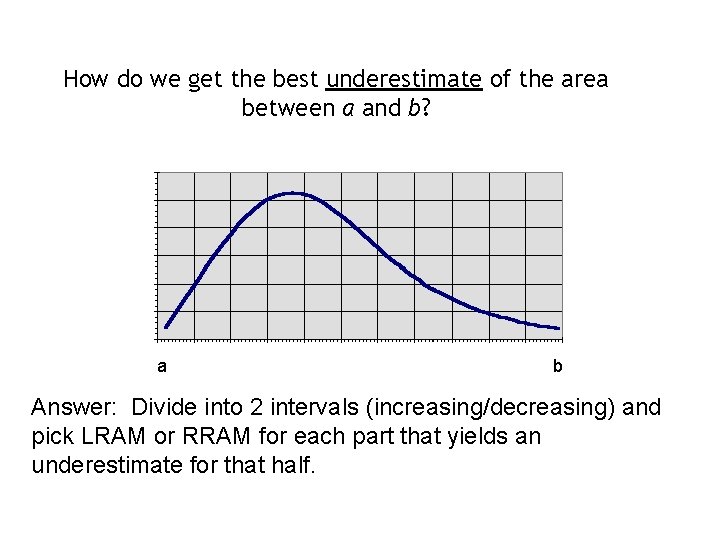
How do we get the best underestimate of the area between a and b? a b Answer: Divide into 2 intervals (increasing/decreasing) and pick LRAM or RRAM for each part that yields an underestimate for that half.