Year 8 Lockdown lessons Finding the nth term

Year 8 Lockdown lessons

Finding the nth term rule What is the nth term rule for the sequence below? -3, 1, 5, 9…. = 4 n – 7 4, 8, 12, 16 = 4 n Can you rem the l ast l ember esso n? ?

Week 6: Lesson 3 Sequences problem solving

Other sequences For each sequence below you need to; a) Find the next 2 terms b) Describe how you found them 1) 1 , 4 , 9 , 16 , 25 36, 49 Square numbers 2) 1 , 2 , 4 , 7 , 11 16, 22 Add an extra 1 each time (+1, +2, +3…) 3) 1 , 8 , 27 , 64 , 125, 216 Cube numbers 4) M , T , W , T , F S, S Days of the week! 5) 1 , 2 , 3 , 5 8, 13 Fibonacci sequence

The Fibonacci sequence In this sequence each term is made by adding the two previous terms together. 1, 1, 2, 3, 5, 8, 13, 21, 2, 4, 6, 10, 16, 26, 42, 68,

The Fibonacci sequence 1) What is the 5 th term in the classic Fibonacci sequence? 1 1 2 3 5 2) A Fibonacci sequence starts with 3, 7, 10… what are the next 3 terms? 3 7 10 17 27 44 3) A Fibonacci sequence starts with a, b, a+2 b… what are the next 2 terms? a b a+2 b 2 a+3 b 3 a+5 b

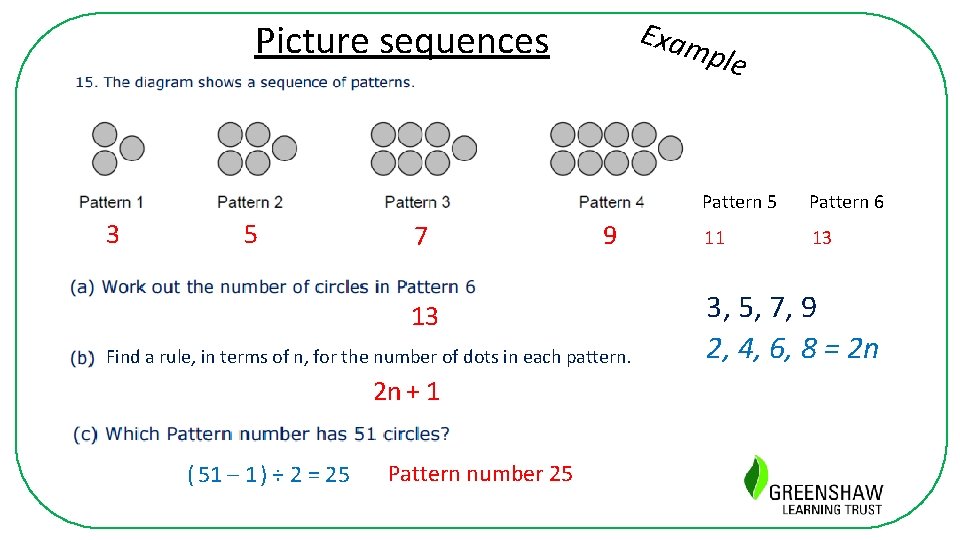
Exam Picture sequences 3 5 7 ple 9 13 Find a rule, in terms of n, for the number of dots in each pattern. 2 n + 1 ( 51 – 1 ) ÷ 2 = 25 Pattern number 25 Pattern 6 11 13 3, 5, 7, 9 2, 4, 6, 8 = 2 n

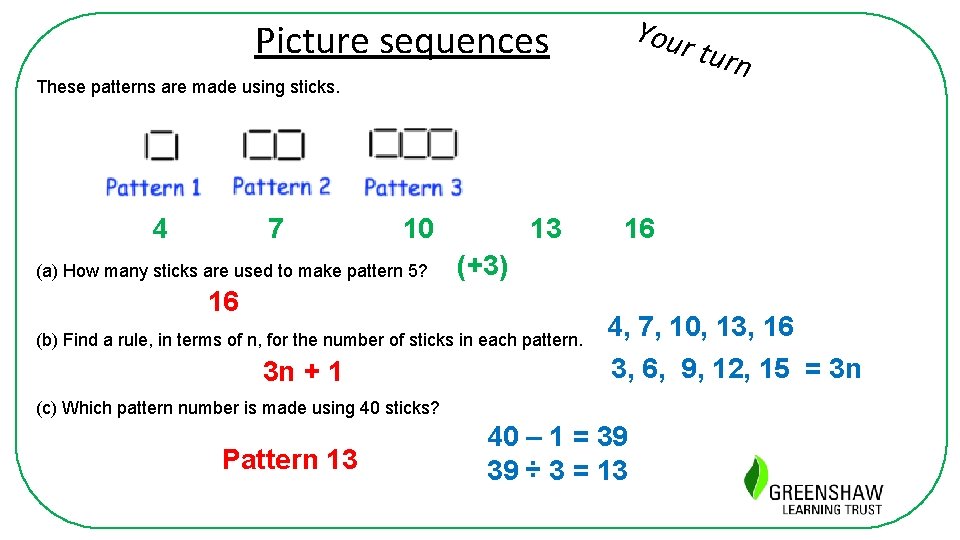
Your Picture sequences These patterns are made using sticks. 7 4 10 (a) How many sticks are used to make pattern 5? 13 16 (+3) 16 (b) Find a rule, in terms of n, for the number of sticks in each pattern. 3 n + 1 4, 7, 10, 13, 16 3, 6, 9, 12, 15 = 3 n (c) Which pattern number is made using 40 sticks? Pattern 13 turn 40 – 1 = 39 39 ÷ 3 = 13

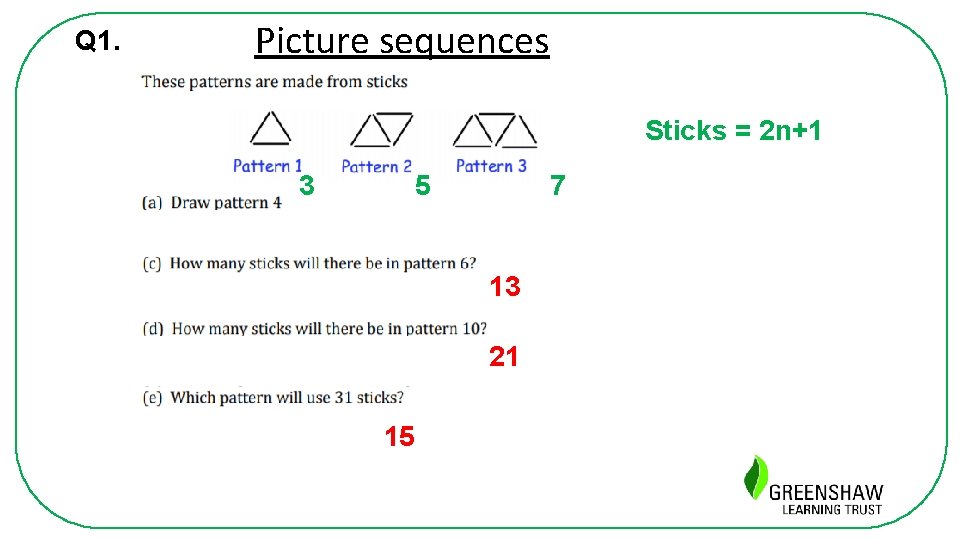
Q 1. Picture sequences Sticks = 2 n+1 3 5 7 13 21 15

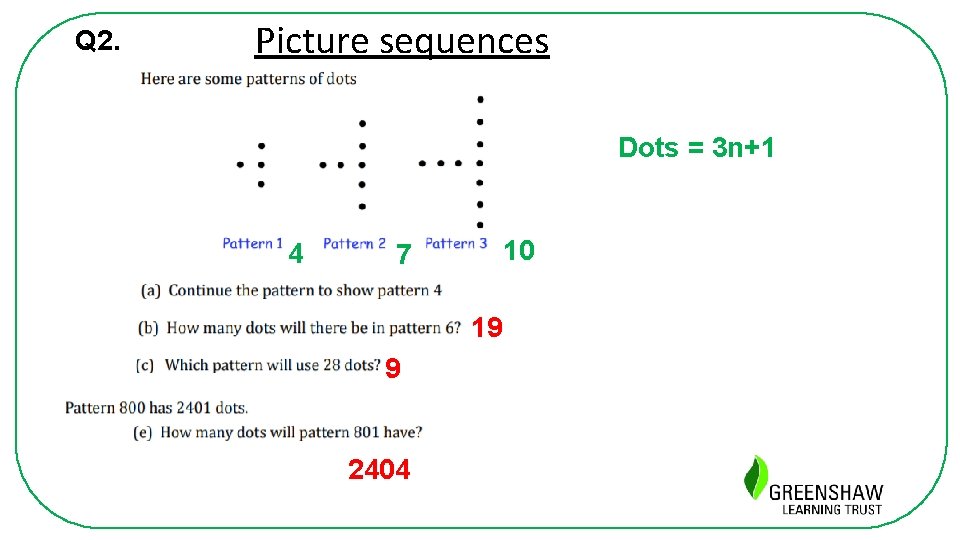
Q 2. Picture sequences Dots = 3 n+1 4 10 7 19 9 2404

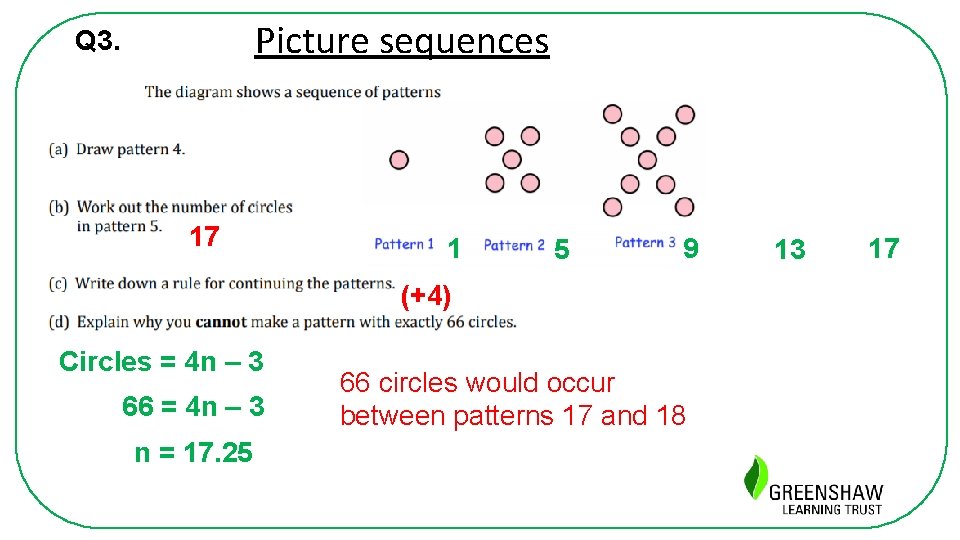
Picture sequences Q 3. 17 1 5 9 (+4) Circles = 4 n – 3 66 = 4 n – 3 n = 17. 25 66 circles would occur between patterns 17 and 18 13 17

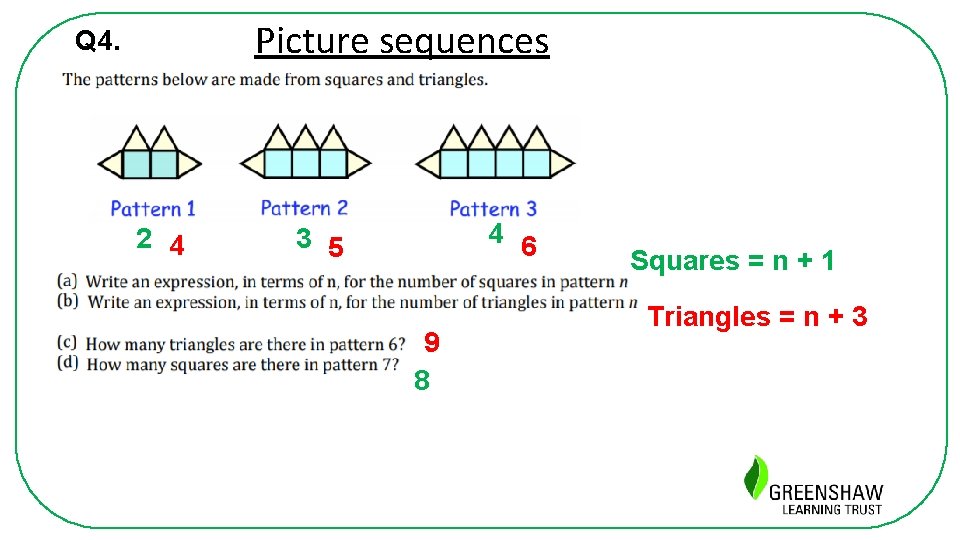
Picture sequences Q 4. 2 4 4 6 3 5 9 8 Squares = n + 1 Triangles = n + 3

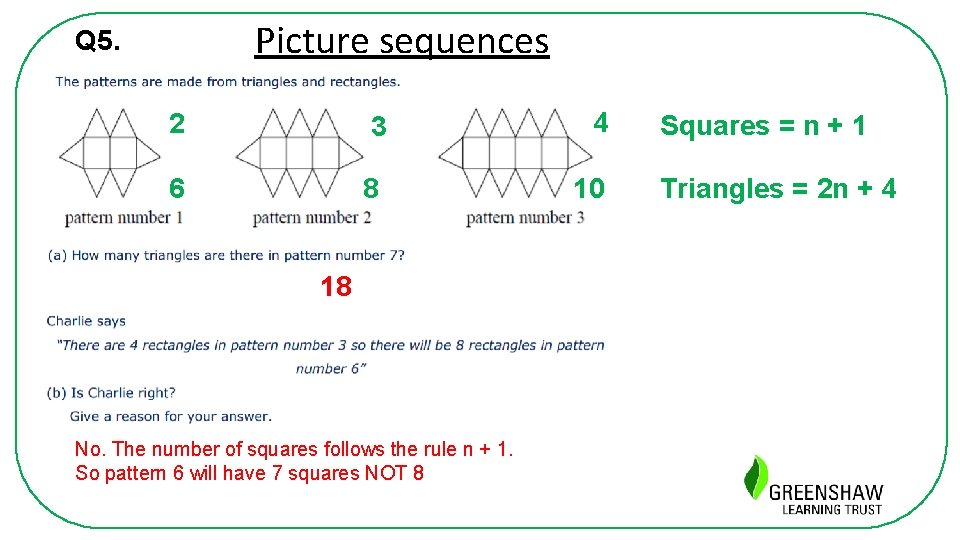
Picture sequences Q 5. 2 3 4 6 8 10 18 No. The number of squares follows the rule n + 1. So pattern 6 will have 7 squares NOT 8 Squares = n + 1 Triangles = 2 n + 4

Year 8 Lockdown lessons

Challenge 1 4, 8, 12, 64 (n 2) 4 n Odd x odd = odd even x even = even 4 n = even + odd = odd even + even = even

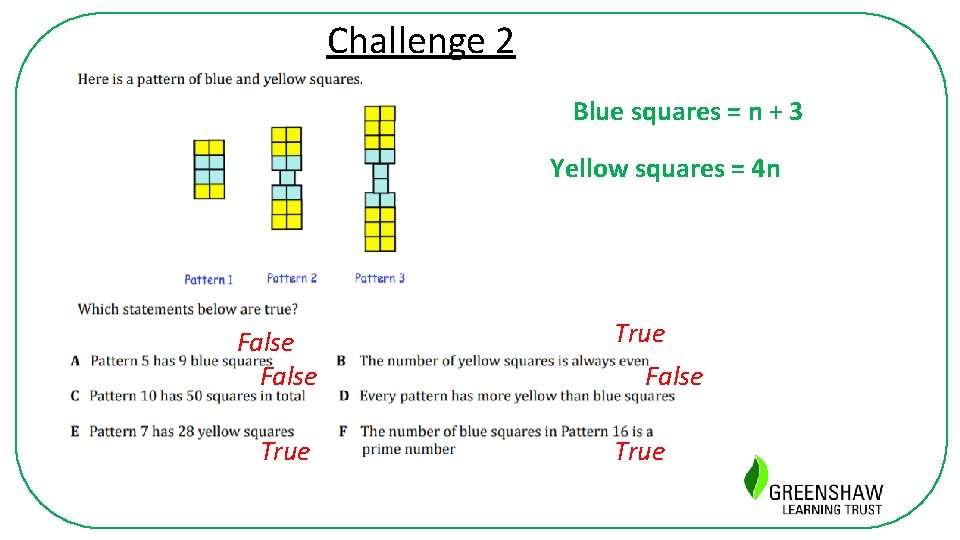
Challenge 2 Blue squares = n + 3 Yellow squares = 4 n False True False

Challenge 3 23, 29, 35 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40