Year 8 Laws of Indices Dr J Frost



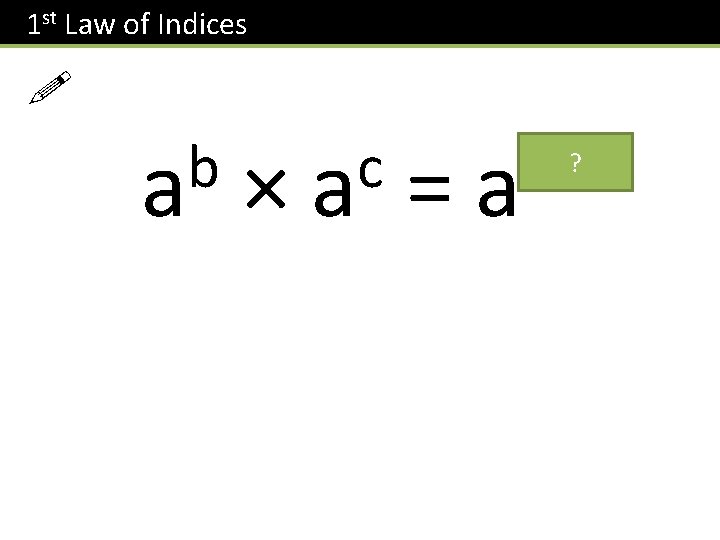

















- Slides: 23

Year 8 Laws of Indices Dr J Frost (jfrost@tiffin. kingston. sch. uk) Last modified: 29 th August 2015

Terminology Recap ! “Base” ? 4 3 “Power” or “index” ? (plural: “indices”) or “exponent” ! We say this as “ 3 to the power of 4” or “ 3 raised to the power of 4” or “ 3 to the 4”. The whole expression is sometimes (confusingly) referred to as a ‘power’ or ‘power expression’.

Multiplying Power Expressions with the Same Base 5 3 4 3 × How would I write this multiplication out in full? Therefore, how could I write the result of this multiplication in the form 3 k? 9 3 ?
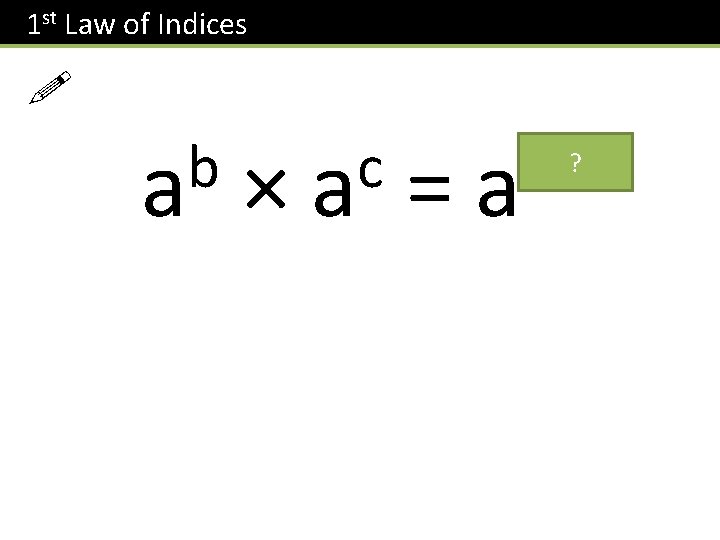
1 st Law of Indices ! b a × c a = b+c a ?

Dividing power expressions with the same base 7 4 2 4 How would I write this multiplication out in full? Therefore, how could I write the result of this multiplication in the form 4 k? 5 4 ?

2 nd Law of Indices ! b a c a = ? b-c a

Raising a power to a power ! 2 3 (4 ) How would I write this multiplication out in full? Therefore, how could I write the result of this multiplication in the form 4 k? 6 4 ?

3 rd Law of Indices ! b c (a ) = bc a ?

Zero and negative indices Is there a pattern we can see that will help us out? 0 3 -1 3 At this point, it doesn’t make sense to say “Multiply 3 by itself negative 1 times”. We’ll have to use a different approach! 33 = 27 2 3 =9 1 3 =3 30 = 1? 3 -1 = 1? 3 3 -2 = 19?

Final Laws of Indices ! 1 a =a 0 a =1 -b a = 1 b a

Mastermind Occupation: Student Favourite Teacher: Dr Frost Specialist Subject: Laws of Indices

Instructions: Everyone starts by standing up. You’ll get a question with a time limit to answer. If you run out of time or get the question wrong, you sit down. The winner is the last man standing. Start Warm 3 4 7 3 4 = ? 212 2 Question × 2 = ? 2 (2 ) Question > > up: 26 Start ? 3 = 2 3 > 2 Question

a b 47 ×Start 43 = ? 410 Start 5 (3 )2 = ? 310 Question > d 57 Start 4 = 5 ? 3 5 Question > c Question > e Start 4 7 × 76 =? 710 f Question > g Start 2)2 = ? 24 (2 Question > h 91 Start? 9 1 = 9 Question > 92 Start 6 )3 = ? (4 Question > 418 Start _1_ -1 ? > 2 Question 2 =

a b 77 ×Start 7 -2 =? 75 Start 3 -2 = ? -6 (5 ) 5 Question > d 87 Start? 9 = 8 -2 8 Question > c e Start -2 8 × 84 =? 82 f 2 Start _1_ -3 2 =? Question > g Start 0 =? 5 1 > Question 10 Start? 3 5 = 10 Question > 10 Question 8 > h Start _1_ -2 ? > 4 = 16 Question

a Start -2 × 4 -2 = ? > 4 4 Question b -4 d 101 Start 10 ? 4 = Question > 10 3 Start -2)-2 = ? 3 Question >4 (3 e Start 4 1 × 16 =? 110 c f Question > =1 g Start _1_ -3 2 -6 (5 Question ) =5? >56 = 9 -2 Start? 0 =9 = Question > -2 9 1 Start Question > INSTANT DEATH h Start _1_ -3 ? > 3 = 27 Question

a b Start 0 ? 5 =1 Start 0 (3 )2 = ? 1 Question > d 51 x. Start 52 x 53 Question =? 56 > c Question > e Start 4 (2 × 26)2 =? f Question > 220 g Start 3 × 2 3 )3 = (2 Question >? 218 50 Start? 2 =5 > -2 Question 5 Start 1 ((4 )2)3 =? Question > h 46 Start _1_ -4 ? > 3 = 81 Question

a 47 ×Start 43 ? = Question > 2 4 48 d 58 ×Start 58 ? = Question > 51 × 5 - 16 5 1 b c (35 Start ) = 3? 17 (73 Start ) = 7? 3 4 Question > e 33 ((32 Start )2)2= 3? 6 Question > 2 3 3 Question > f (72) 3 (71 Start ) × 74 =? 3 Question > 2 75 (7 ) 1

Challenges 1 2 ? 3 ? 4 ? ? 5 ?

Exercise 1 Please ensure you write out the question. 3 1 Simplify the following. ? ? ? ? ? 4 2 Simplify the following. ? ? Evaluate the following (i. e. give as a fraction or integer with no power) ? N 2 ? ? ? Simplify the following. ? ? N 1 ? ?

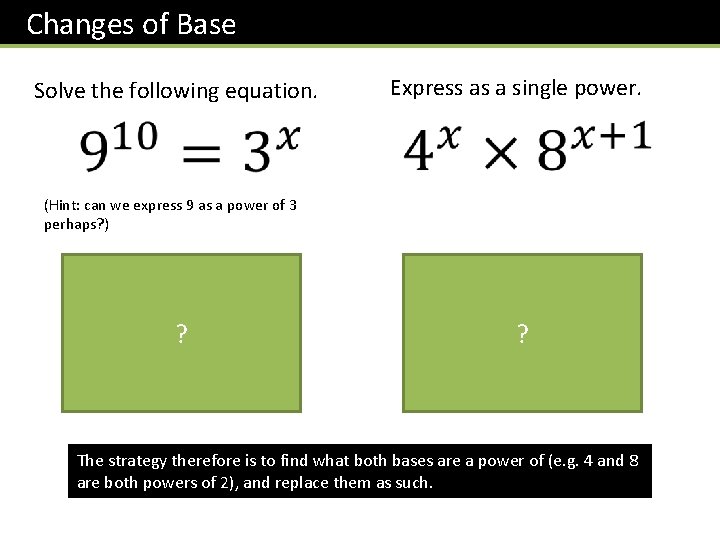
Changes of Base Solve the following equation. Express as a single power. (Hint: can we express 9 as a power of 3 perhaps? ) ? ? The strategy therefore is to find what both bases are a power of (e. g. 4 and 8 are both powers of 2), and replace them as such.

A few more examples… Solve ? ? Express as a single power of 3: ?

Test Your Understanding 8 2 x 4 = 4 27 x = 4? x 8 = = x 9 x = 6? 12 4 x 3 = 100 27 ? x = 300 x = 8? Express as a single power: ? ?

Exercise 2 Please ensure you write out the question. Solve the following. 1 2 3 4 5 6 Express as a single power. ? ? ? 13 14 8 9 10 11 ? ? ? 15 ? N Solve the following. 7 ? 12 ? ? ? ?