Year 8 Data Handling 2 Dr J Frost







- Slides: 29

Year 8: Data Handling 2 Dr J Frost (jfrost@tiffin. kingston. sch. uk) Learning Outcomes: To understand stem and leaf diagrams, frequency polygons, box plots and cumulative frequency graphs. Last modified: 11 th December 2014

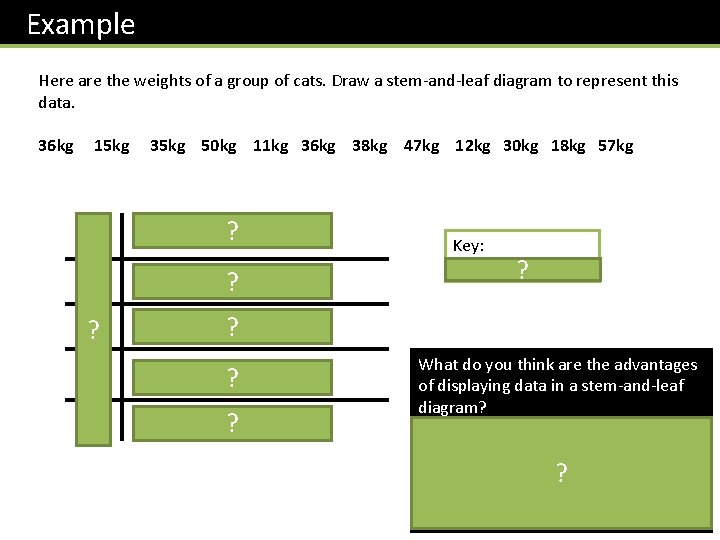
Stem and Leaf Diagram - What is it? Suppose this “stem and leaf diagram” represents the lengths of beetles. 1 2 3 4 5 4 1 2 4 5 2 5 6 6 6 7 7 8 8 0 1 2 2 4 5 6 7 7 8 0 1 1 2 Value represented = 4. 5 cm ? These numbers represent the first digit of the number. The key tells us how two digits combine. Key: 2 | 1 means 2. 1 cm The numbers must be in order. These numbers represent the second.

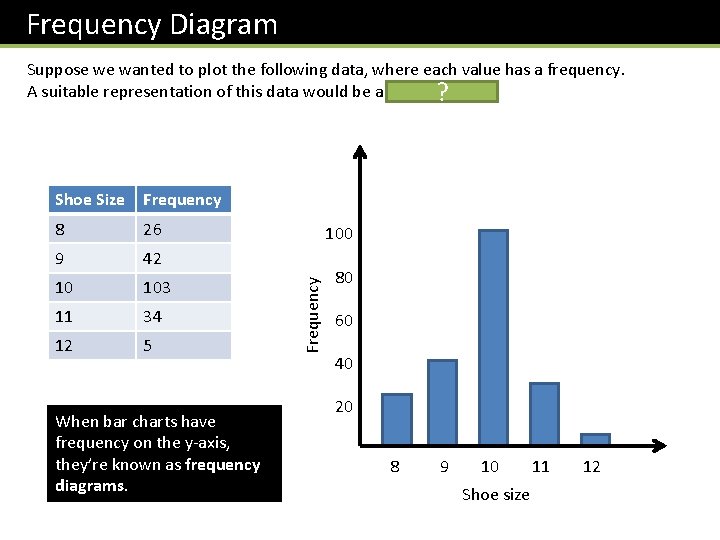
Example Here are the weights of a group of cats. Draw a stem-and-leaf diagram to represent this data. 36 kg 15 kg 1 35 kg 50 kg 11 kg 36 kg 38 kg 47 kg 12 kg 30 kg 18 kg 57 kg 1 2 5 8 ? ? 2 ? 3 0 5 6 6 8 ? 4 7 ? 5 0 7 ? Key: 3 | 8 means 38 kg ? What do you think are the advantages of displaying data in a stem-and-leaf diagram? • Shows how the data is spread out. • Identifies gaps in ? the values. • All the original data is preserved (i. e. we don’t ‘summarise’ in any way).

Your turn Here is the brain diameter of a number of members of 8 IW. Draw a stem and leaf diagram representing this data. 1. 3 cm 2. 1 cm 5. 3 cm 2. 0 cm 1 3 3 7 9 ? 2 0 1 ? 3 2 3 ? 4 2 6 ? 5 3 ? 1. 7 cm ? ? Median width = 2. 1 cm ? Lower Quartile = 1. 7 cm ? Upper Quartile = 4. 2 cm 3. 3 cm 3. 2 cm 1. 3 cm 4. 6 cm 1. 9 cm Key: 3 | 8 means 3. 8 cm ?

Exercises Q 1 on your provided worksheet. (Ref: Yr 8 -Data. Handling. Worksheet. doc)

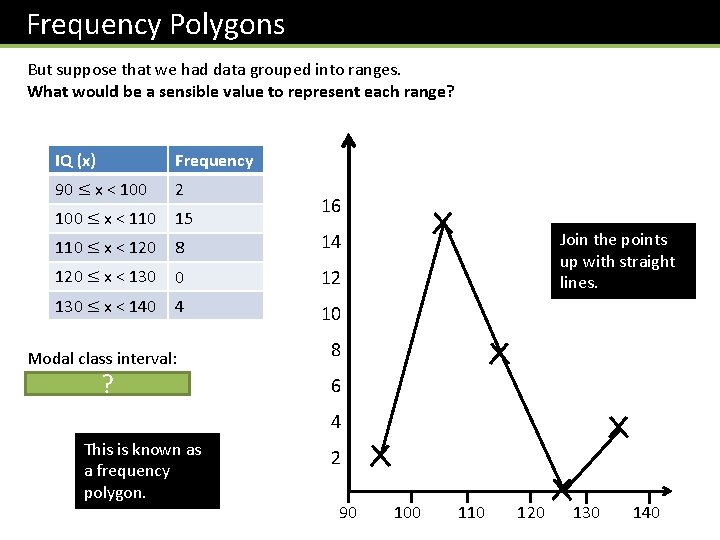
Frequency Diagram Suppose we wanted to plot the following data, where each value has a frequency. A suitable representation of this data would be a bar chart. ? Frequency 8 26 9 42 10 103 11 34 12 5 When bar charts have frequency on the y-axis, they’re known as frequency diagrams. 100 Frequency Shoe Size 80 60 40 20 8 9 10 11 12 Shoe size

Frequency Polygons But suppose that we had data grouped into ranges. What would be a sensible value to represent each range? IQ (x) Frequency 90 ≤ x < 100 2 100 ≤ x < 110 15 110 ≤ x < 120 8 14 120 ≤ x < 130 0 12 130 ≤ x < 140 4 10 Modal class interval: 100 ≤ x < ? 110 16 Join the points up with straight lines. 8 6 4 This is known as a frequency polygon. 2 90 100 110 120 130 140

Frequency Polygons – Exercises on sheet Q 1 Q 2 ? b) 30 < x ≤ 40 ? c) 16% ? ? b) 20 < x ≤ 30 ? c) 16% ?

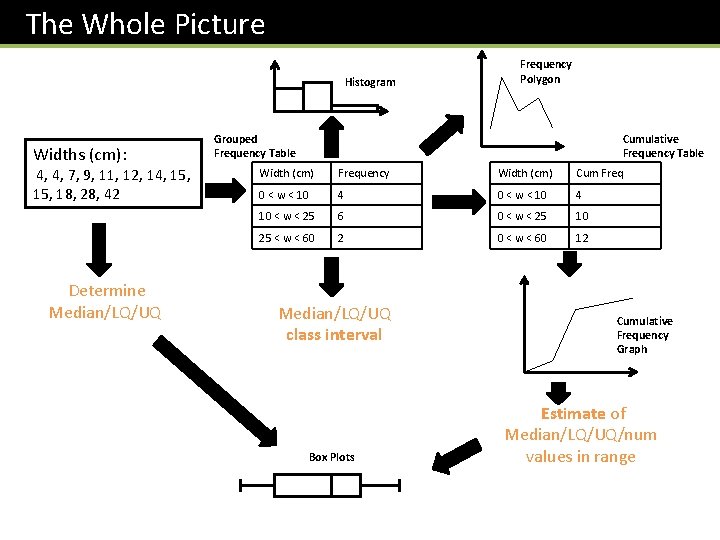
The Whole Picture Histogram Widths (cm): 4, 4, 7, 9, 11, 12, 14, 15, 18, 28, 42 Determine Median/LQ/UQ Frequency Polygon Cumulative Frequency Table Grouped Frequency Table Width (cm) Frequency Width (cm) Cum Freq 0 < w < 10 4 10 < w < 25 6 0 < w < 25 10 25 < w < 60 2 0 < w < 60 12 Median/LQ/UQ class interval Box Plots Cumulative Frequency Graph Estimate of Median/LQ/UQ/num values in range

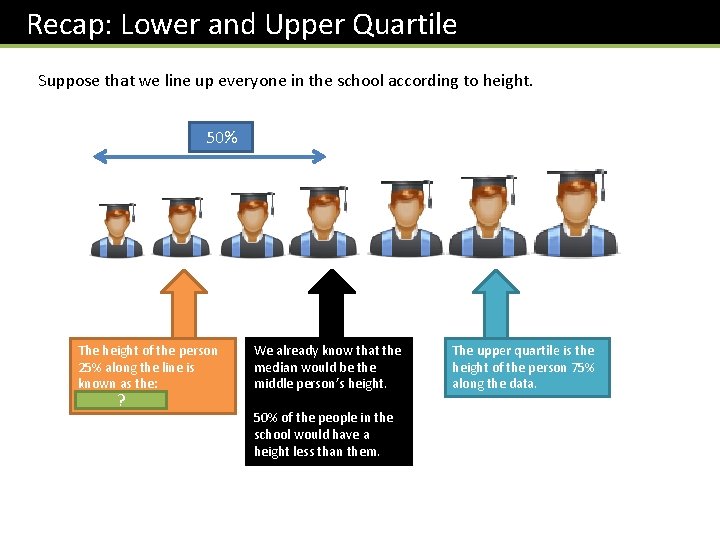
Recap: Lower and Upper Quartile Suppose that we line up everyone in the school according to height. 50% The height of the person 25% along the line is known as the: lower quartile ? We already know that the median would be the middle person’s height. 50% of the people in the school would have a height less than them. The upper quartile is the height of the person 75% along the data.

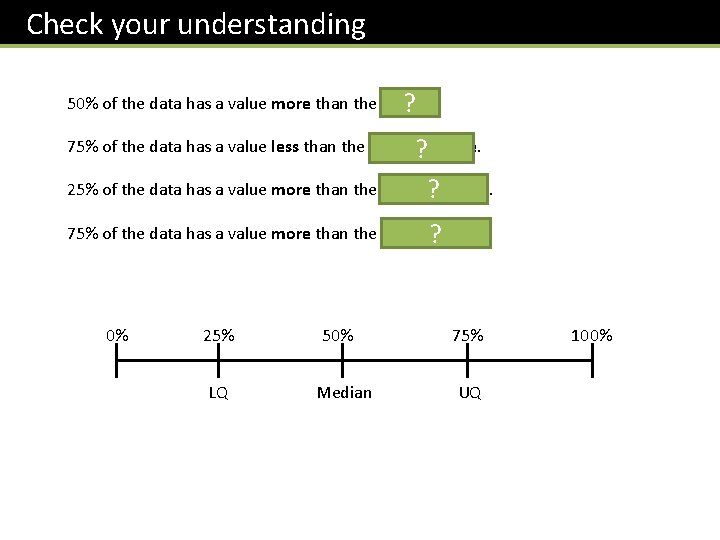
Check your understanding 50% of the data has a value more than the median. ? 75% of the data has a value less than the upper ? quartile. 25% of the data has a value more than the upper ? quartile. 75% of the data has a value more than the lower quartile. ? 0% 25% LQ 50% Median 75% UQ 100%

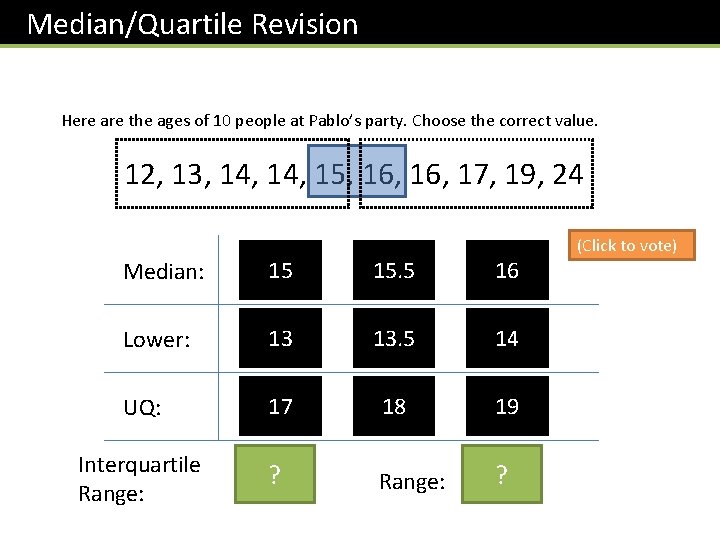
Median/Quartile Revision Here are the ages of 10 people at Pablo’s party. Choose the correct value. 12, 13, 14, 15, 16, 17, 19, 24 Median: 15 15. 5 16 Lower: 13 13. 5 14 UQ: 17 18 19 Interquartile Range: 3? Range: ? 12 (Click to vote)

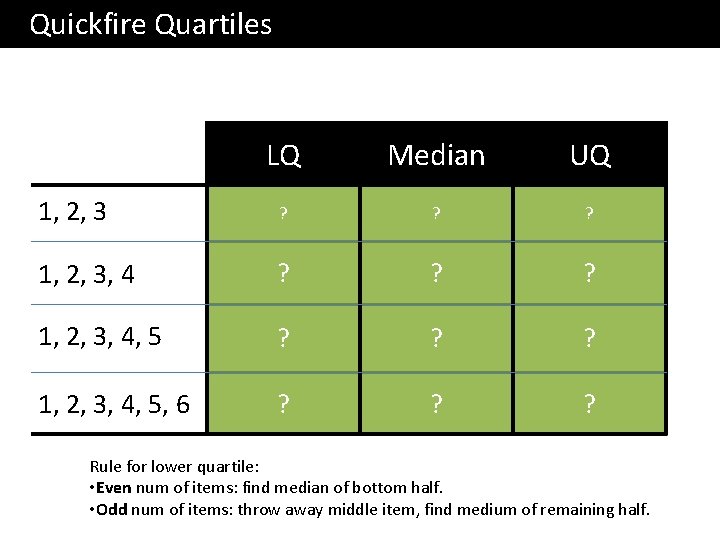
Quickfire Quartiles LQ Median UQ 1? 2? 3? 1, 2, 3, 4 ? 1. 5 ? 2. 5 ? 3. 5 1, 2, 3, 4, 5 1. 5 ? 2? 4. 5 ? 2? 3. 5 ? 5? 1, 2, 3, 4, 5, 6 Rule for lower quartile: • Even num of items: find median of bottom half. • Odd num of items: throw away middle item, find medium of remaining half.

What if there’s lots of items? There are 31 items, in order of value. What items should we use for the median and lower/upper quartiles? 0 1 1 2 4 5 5 6 7 8 10 14 14 15 16 17 29 31 37 38 39 40 41 43 44 LQ th item Use the 8 ? Median ? th item Use the 16 UQ ? th item Use the 24

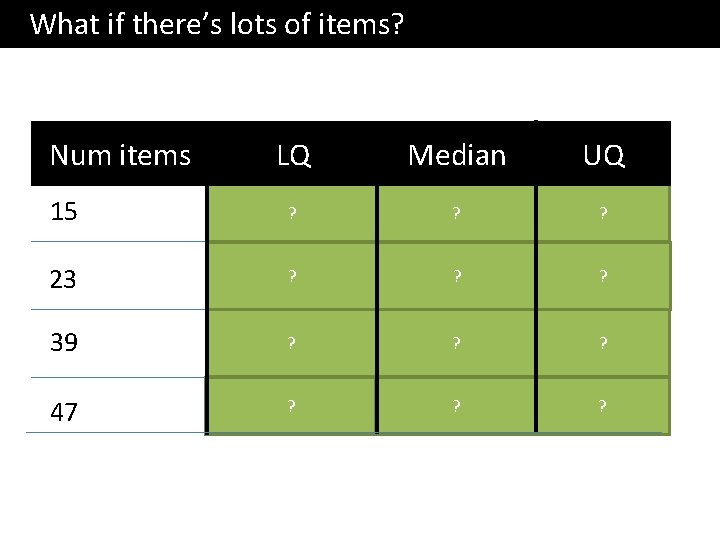
What if there’s lots of items? Num items LQ Median UQ 15 4 th? 8? th 12 23 6 th? 12? th 18? th 39 10? th 20? th 30? th 47 12? th 24? th 36? th

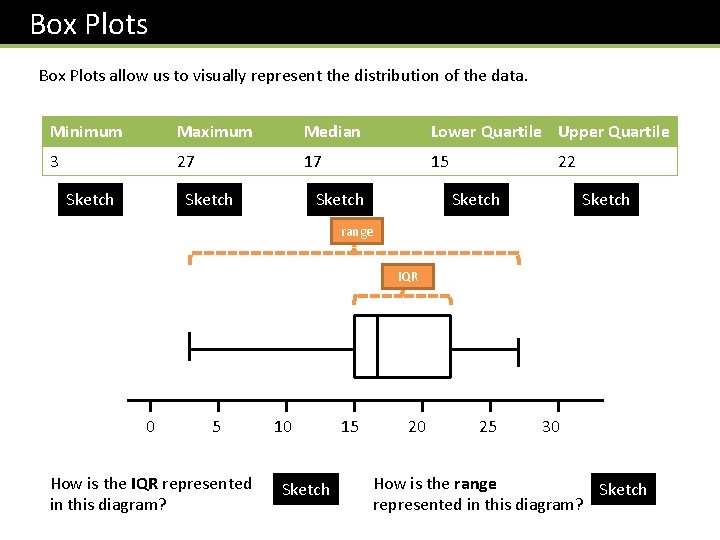
Box Plots allow us to visually represent the distribution of the data. Minimum Maximum Median Lower Quartile Upper Quartile 3 27 17 15 Sketch 22 Sketch range IQR 0 5 10 15 20 25 30 How is the IQR represented in this diagram? Sketch How is the range Sketch represented in this diagram?

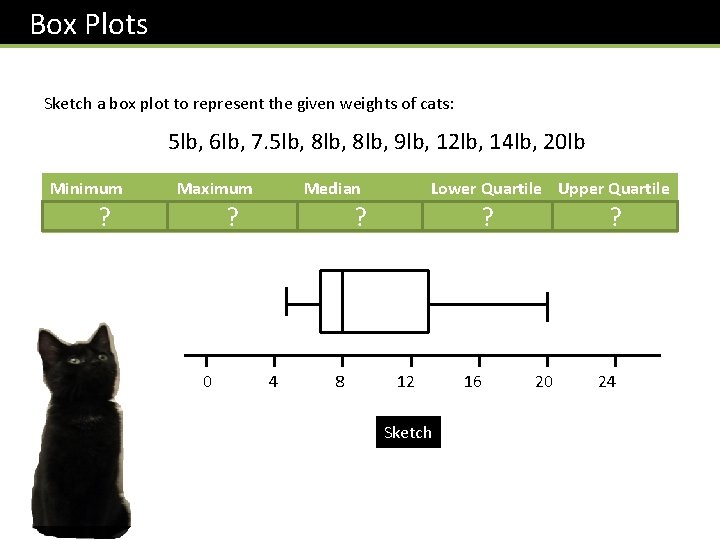
Box Plots Sketch a box plot to represent the given weights of cats: 5 lb, 6 lb, 7. 5 lb, 8 lb, 9 lb, 12 lb, 14 lb, 20 lb Minimum 5 ? Maximum 20 ? Median 8 ? Lower Quartile Upper Quartile 6. 75 ? 13 ? 0 4 8 12 16 20 24 Sketch

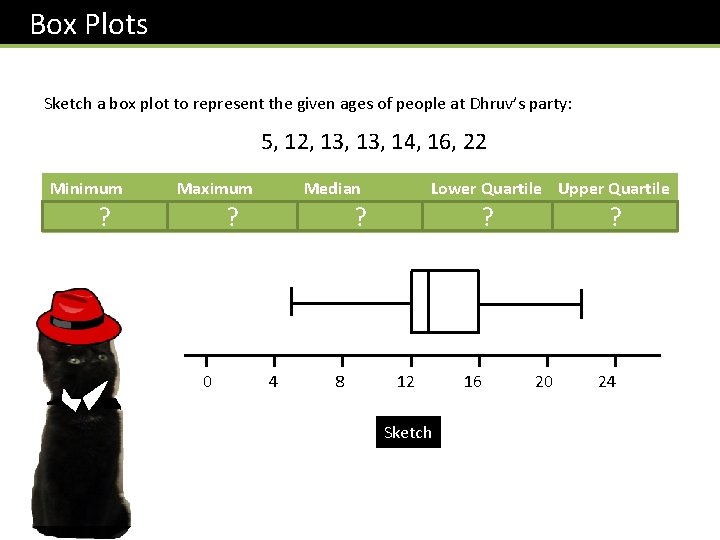
Box Plots Sketch a box plot to represent the given ages of people at Dhruv’s party: 5, 12, 13, 14, 16, 22 Minimum 5 ? Maximum 22 ? Median 13 ? Lower Quartile Upper Quartile 12 ? 16 ? 0 4 8 12 16 20 24 Sketch

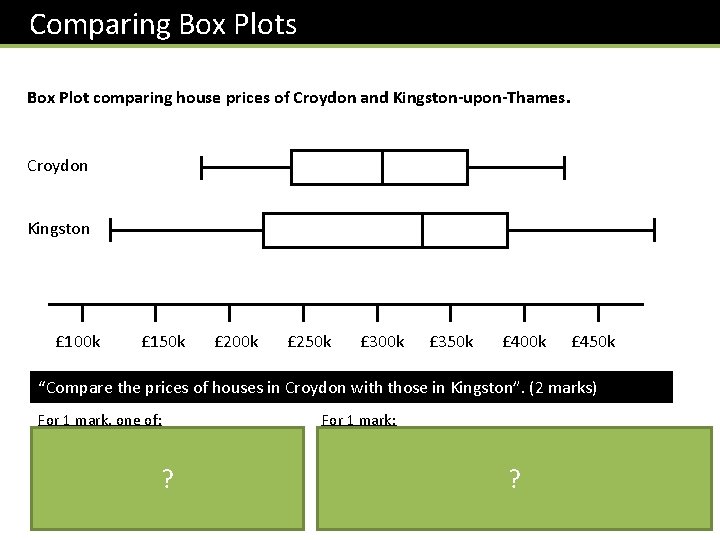
Comparing Box Plots Box Plot comparing house prices of Croydon and Kingston-upon-Thames. Croydon Kingston £ 100 k £ 150 k £ 200 k £ 250 k £ 300 k £ 350 k £ 400 k £ 450 k “Compare the prices of houses in Croydon with those in Kingston”. (2 marks) For 1 mark, one of: • In interquartile range of house prices in Kingston is greater than Croydon. • The range of house prices in Kingston is greater than Croydon. ? For 1 mark: • The median house price in Kingston was greater than that in Croydon. • (Note that in old mark schemes, comparing the minimum/maximum/quartiles would have been acceptable, but currently, you MUST compare the median) ?

100 m times at the 2012 London Olympics Modal class interval 10. 05 < t ≤ 10. 2 ? ? Median class interval 10. 05 < t ≤ 10. 2 ? Estimate of mean 10. 02 Time (s) Frequency 9. 6 < t ≤ 9. 7 1 9. 7 < t ≤ 9. 9 4 9. 9 < t ≤ 10. 05 10 10. 05 < t ≤ 10. 2 17 TOTAL Cum Freq 1? 5? 15? 32? ?

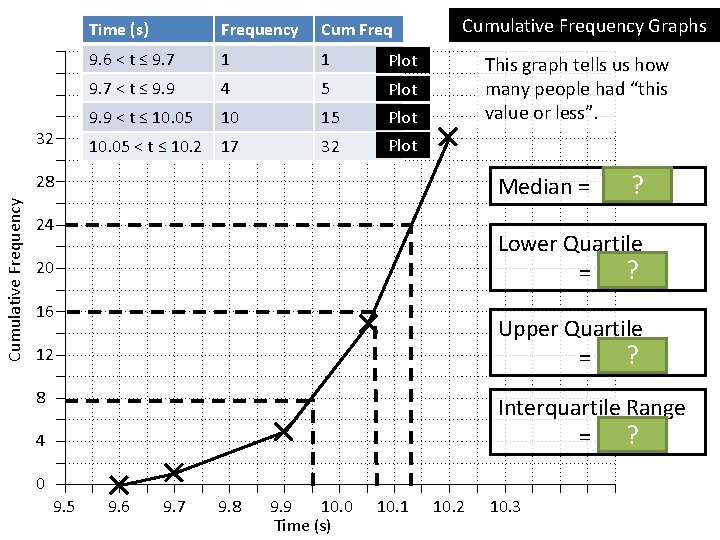
32 Cumulative Frequency 28 24 20 16 12 8 4 Time (s) Frequency Cum Freq 9. 6 < t ≤ 9. 7 1 1 Plot 9. 7 < t ≤ 9. 9 4 5 Plot 9. 9 < t ≤ 10. 05 10 15 Plot 10. 05 < t ≤ 10. 2 17 32 Plot Cumulative Frequency Graphs This graph tells us how many people had “this value or less”. Median = 10. 07 s ? Lower Quartile ? = 9. 95 s Upper Quartile ? = 10. 13 s Interquartile Range ? = 0. 18 s 0 9. 5 9. 6 9. 7 9. 8 9. 9 10. 0 10. 1 10. 2 10. 3 Time (s)

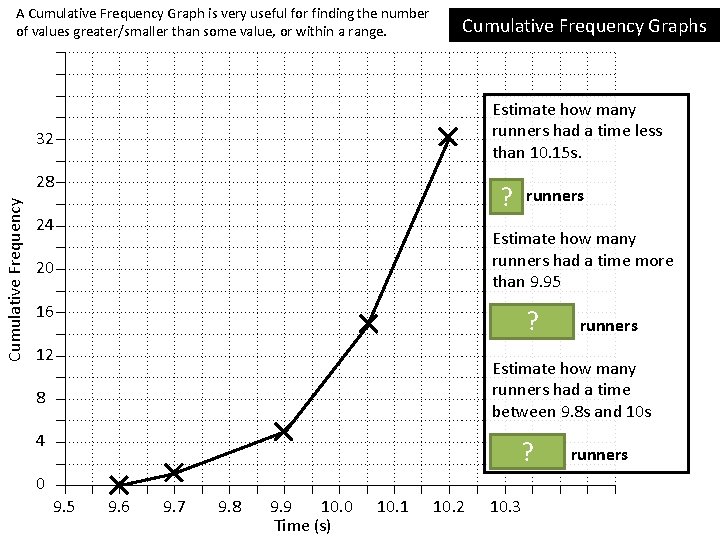
A Cumulative Frequency Graph is very useful for finding the number of values greater/smaller than some value, or within a range. 32 Cumulative Frequency 28 24 20 16 12 8 4 Cumulative Frequency Graphs Estimate how many runners had a time less than 10. 15 s. 26 ? runners Estimate how many runners had a time more than 9. 95 32 – ? 8 = 24 runners Estimate how many runners had a time between 9. 8 s and 10 s 11 –? 3 = 8 runners 0 9. 5 9. 6 9. 7 9. 8 9. 9 10. 0 10. 1 10. 2 10. 3 Time (s)

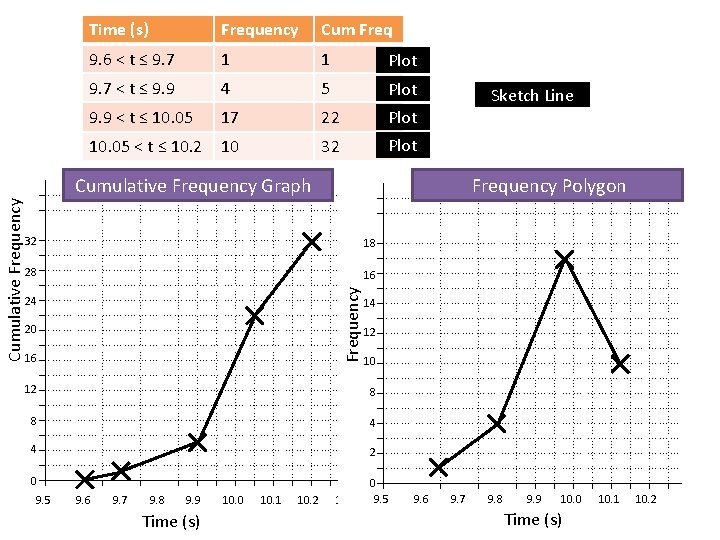
Time (s) Frequency Cum Freq 9. 6 < t ≤ 9. 7 1 1 Plot 9. 7 < t ≤ 9. 9 4 5 Plot 9. 9 < t ≤ 10. 05 17 22 Plot 10. 05 < t ≤ 10. 2 10 32 Plot Cumulative Frequency Graph Frequency Polygon 18 28 16 Frequency 32 24 20 16 Sketch Line 14 12 10 12 8 8 4 4 2 0 0 9. 5 9. 6 9. 7 9. 8 9. 9 10. 0 10. 1 10. 2 9. 5 9. 6 9. 7 9. 8 9. 9 10. 0 10. 1 10. 2 10. 3 Time (s)

Worksheet Cumulative Frequency Graphs Printed handout. Q 5, 6, 7, 8, 9, 10 Reference: GCSE-Grouped. Data. Cum. Freq

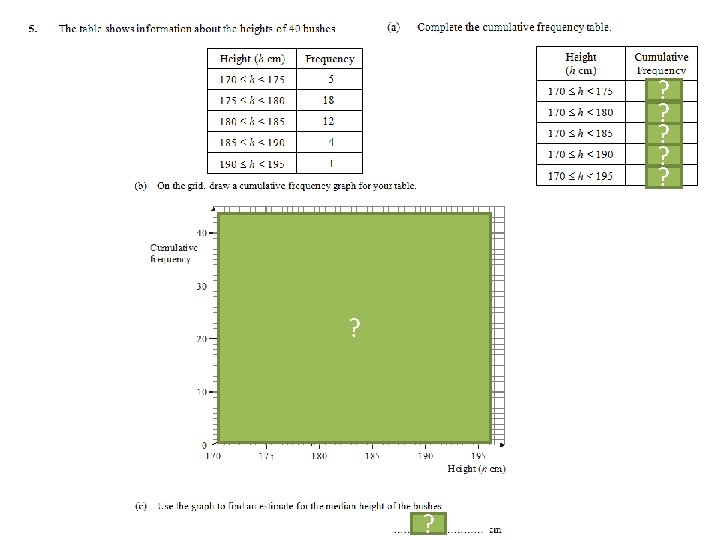
5? 23 ? 35 ? 39 ? 40 ? ? 179 ?

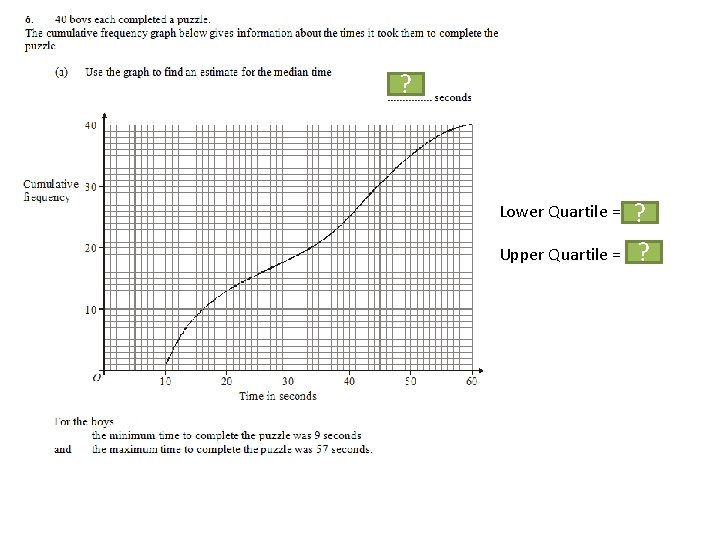
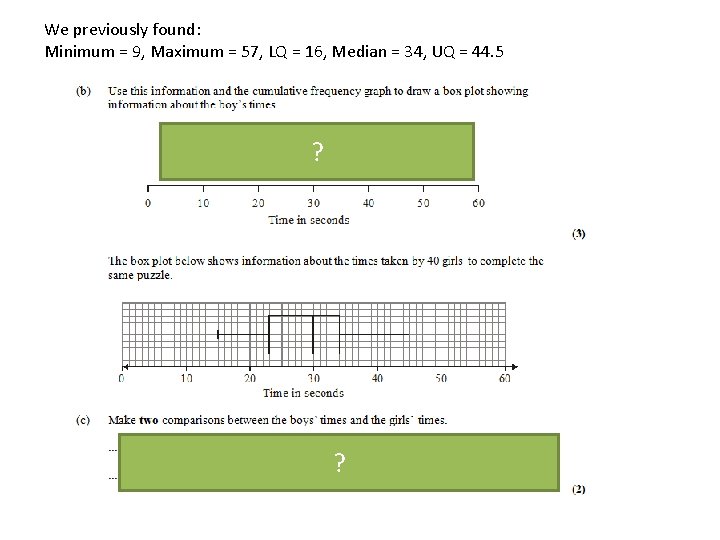
34 ? Lower Quartile = 16 ? Upper Quartile = 44. 5 ?

We previously found: Minimum = 9, Maximum = 57, LQ = 16, Median = 34, UQ = 44. 5 ? 1 mark: Range/interquartile range of boys’ times is greater. 1 mark: Median of boys’ times is greater. ?

44 100 134 153 160 ? ? 30 ? ? ?

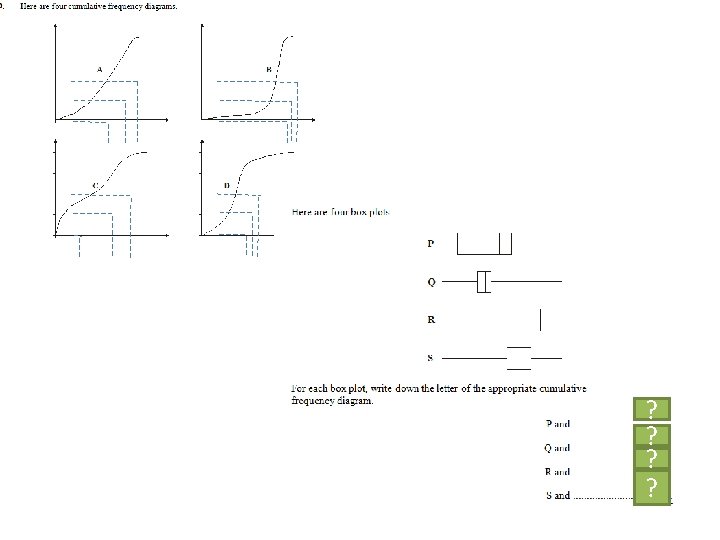
C? D? B? A?