Year 7 Sequences Dr J Frost jfrosttiffin kingston

Year 7 : : Sequences Dr J Frost (jfrost@tiffin. kingston. sch. uk) www. drfrostmaths. com Objectives: Understand term-to-term vs position-to-term rules. Be able to generate terms of a sequence given a formula. Find the formula for a linear sequence. Be able to find a term of an oscillating sequence. Last modified: 22 nd July 2018

www. drfrostmaths. com Everything is completely free. Why not register? Register now to interactively practise questions on this topic, including past paper questions and extension questions (including UKMT). Teachers: you can create student accounts (or students can register themselves), to set work, monitor progress and even create worksheets. With questions by: Dashboard with points, trophies, notifications and student progress. Teaching videos with topic tests to check understanding. Questions organised by topic, difficulty and past paper.

Teacher Guidance Go >

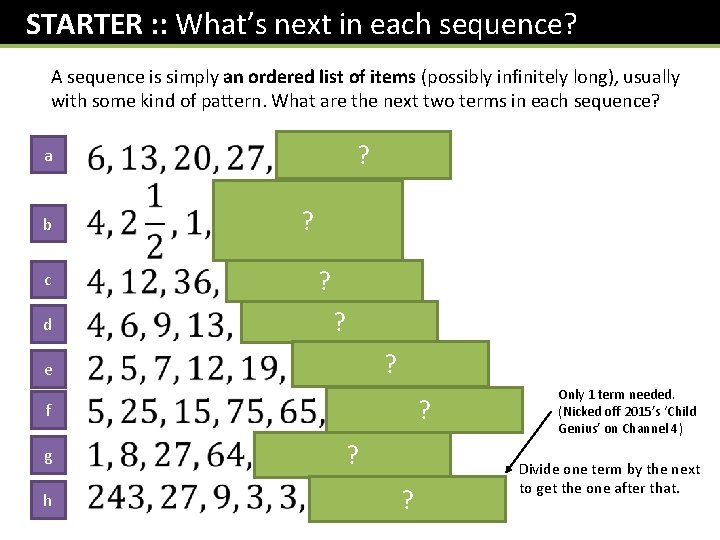
STARTER : : What’s next in each sequence? A sequence is simply an ordered list of items (possibly infinitely long), usually with some kind of pattern. What are the next two terms in each sequence? ? a b c d ? ? e ? f g h ? ? Only 1 term needed. (Nicked off 2015’s ‘Child Genius’ on Channel 4) Divide one term by the next to get the one after that.

Term-to-term rules Some sequences we can generated by stating a rule to say how to generate the next term given the previous term(s). Description First 5 terms The first term of a sequence is 1. +3 to each term to get the next. 1, 4, 7, 10, 13 ? 3, 6, 12, 24, 48 ? The first two terms are 0 and 1. Add the last two terms to get the next. 0, 1, 1, 2, 3 ? (known as the Fibonacci sequence) What might be the disadvantage of using a term-to-term rule? To get a particular term in the sequence, we have to generate all the terms in the sequence before it. This ? is rather slow if you say want to know the 1000 th term!

JMC Puzzle [JMC 2009 Q 11] In a sequence of numbers, each term after the first three terms is the sum of the previous three terms. The first three terms are -3, 0, 2. Which is the first term to exceed 100? A 11 th term B 12 th term C 13 th term D 14 th term E 15 th term Vote (click) A B C D Terms are: -3, 0, 2, -1, 1, 2, 2, 5, 9, 16, 30, 55, 101 E

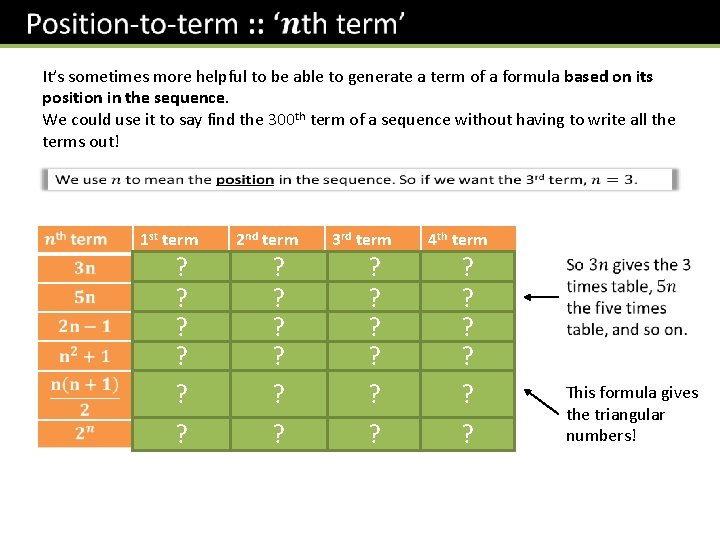
It’s sometimes more helpful to be able to generate a term of a formula based on its position in the sequence. We could use it to say find the 300 th term of a sequence without having to write all the terms out! 1 st term ? ? ? 2 nd term ? ? ? 3 rd term ? ? ? 4 th term ? ? ? This formula gives the triangular numbers!

Check Your Understanding ? ?

Challenge Your Neighbour most e h t r o IT f A MER g sequence! tin interes

Exercise 1 5 1 ? ? 2 6 ? 3 ? ? 4 ? ? N ? (Hint: perhaps represent the first two terms algebraically? )

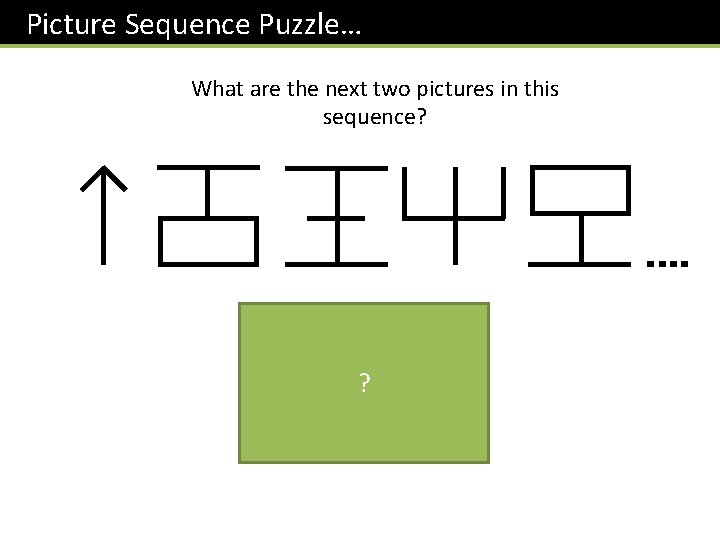
Picture Sequence Puzzle… What are the next two pictures in this sequence? ? It’s the numbers 1, 2, 3, … but reflected. Sneaky!

Generating Sequences on your Calculator! (just for fun)

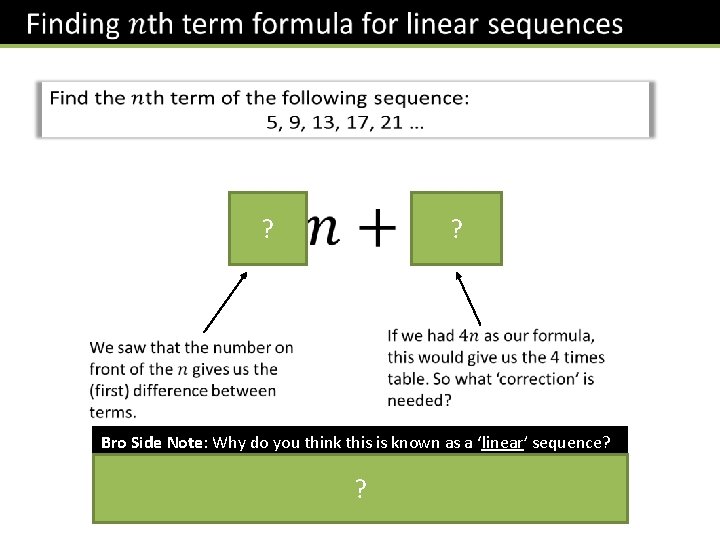
Linear Sequences Today’s title ? ? ? ?

? ? Bro Side Note: Why do you think this is known as a ‘linear’ sequence? If you plotted each position with the term on some axes (e. g. for this sequence (1, 5), (2, 9), (3, 13), (4, 17), …, ? it would form a straight line. The word ‘linear’ means ‘straight’.

More examples ? ? ? Quickfire Questions: 100 th term: ? ? ? ?

Test Your Understanding 100 th term: ? ? ? ? ?

Is a number in the sequence? ? ?

Exercise 2 1 4 ? ? ? ? a b c d e f g c d 5 ? 2 a b c d N ? ? 3 a b ? ? ?

Levelled Game Note to teachers: See the separate pdf for this activity, for suitable printouts and solutions.

Oscillating Sequences There are many places in mathematics where sequences repeat. e. g. tiffintiffintiffin… What is the 60 th letter in this sequence? What is the 100 th letter in this sequence? What is the 175 th letter in this sequence? ‘n’? ‘f’ ? ‘t’?

Oscillating Sequences 1 2 3 4 5 6 7 8 9 10 11 12 tiffintiffintiffin… The sequence repeats every 6 letters. Therefore, if we find the remainder when we divide the position by 6, we can just compare against the first few letters. ? ? ? Bro Mental Tip: 180 is clearly a multiple of 6, so we only have to divide 20 by 6 for the remainder.

Last Digits ? Consider the last digit when the power is 1, 2, 3, 4, … How does the sequence repeat?

Test Your Understanding A ? B ?

Exercise 3 5 1 ? ? a b c d ? 2 N ? 3 a c e ? ? b d 4 ? ? ?

QQQ Time! QQQ