Year 11 Maths enrichment Gradients Contents This enrichment






- Slides: 10

Year 11 Maths enrichment Gradients

Contents This enrichment work is meant to develop your understanding of some GCSE topics and extend them into more advanced ideas. All the methods used are ones that you have learnt or will learn in the Higher GCSE course, but the outcome is part of the A level. Each section should take about 30 mins. Click on the links below to go straight to the section. 1. The gradient at a point 2. The gradient function 3. Pattern hunting 4. Proving the results 1/5/2022 Maths @ Paston © P. R. Brayne 2

1. The gradient at a point How can you calculate the gradient at a point on a graph? We’ll start with the curve y=x 2, and try to find the gradient at (1, 1). You could draw a tangent, and measure the gradient (Now click) 1. 8 1 but this would not be accurate. 1/5/2022 Maths @ Paston © P. R. Brayne 3

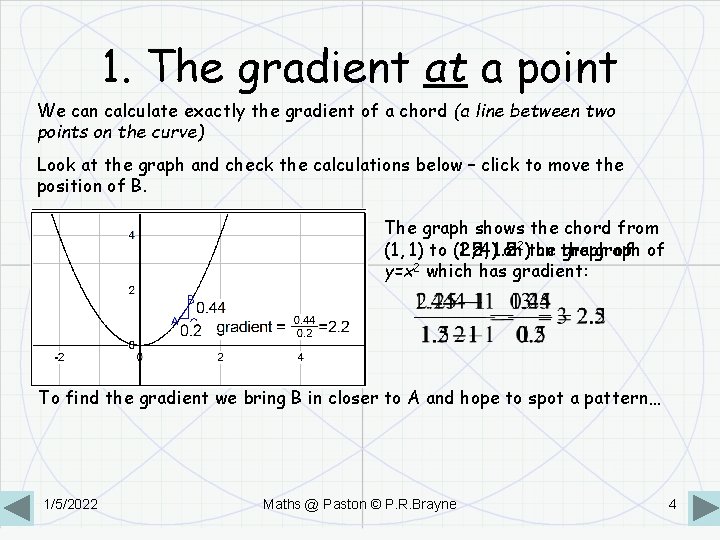
1. The gradient at a point We can calculate exactly the gradient of a chord (a line between two points on the curve) Look at the graph and check the calculations below – click to move the position of B. The graph shows the chord from (1, 1) to (1. 2, (2, 4)1. 2 (1. 5, 1. 5 on 2)the on the graph of of y=x 2 which has gradient: To find the gradient we bring B in closer to A and hope to spot a pattern… 1/5/2022 Maths @ Paston © P. R. Brayne 4

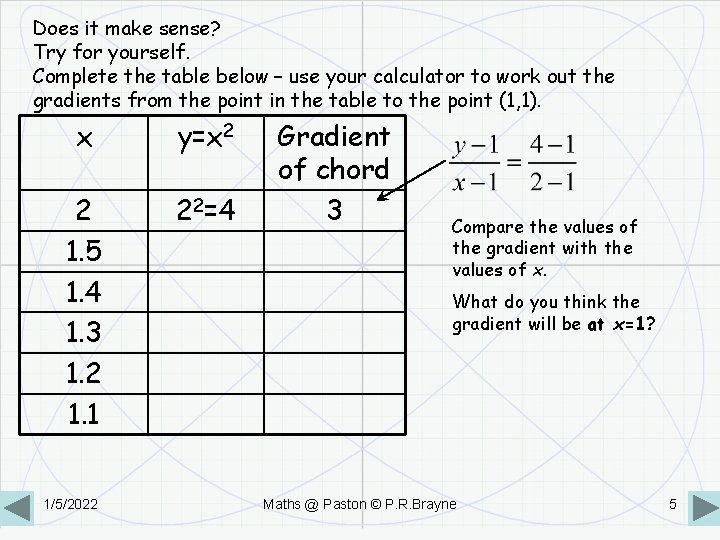
Does it make sense? Try for yourself. Complete the table below – use your calculator to work out the gradients from the point in the table to the point (1, 1). x y=x 2 2 1. 5 1. 4 1. 3 1. 2 1. 1 22=4 1/5/2022 Gradient of chord 3 Compare the values of the gradient with the values of x. What do you think the gradient will be at x=1? Maths @ Paston © P. R. Brayne 5

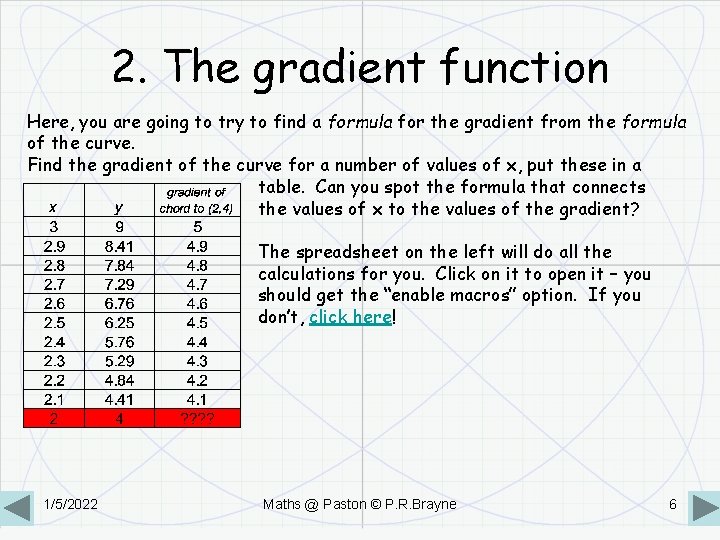
2. The gradient function Here, you are going to try to find a formula for the gradient from the formula of the curve. Find the gradient of the curve for a number of values of x, put these in a table. Can you spot the formula that connects the values of x to the values of the gradient? The spreadsheet on the left will do all the calculations for you. Click on it to open it – you should get the “enable macros” option. If you don’t, click here! 1/5/2022 Maths @ Paston © P. R. Brayne 6

3. Pattern hunting Here you are going to try to find a pattern that connects the formula to its gradient. Use the spreadsheet on the last page to help you find the formulas for the gradients to the curves in the table below Equation y=x 2 y=x 3 y=x 4 y=x 5 y=x 6 Gradient function 1 2 x 3 x 2 4 x 3 5 x 4 6 x 5 Now generalise this to write down a rule: The gradient function of xn is =nxn-1 Test your rule on the spreadsheet for other powers, like x -1, or x 0. 5 Click i for answers 1/5/2022 Maths @ Paston © P. R. Brayne 7

4. Proving the results Now you are actually going to prove some of the earlier results. To do this you need to check some algebra first. Expand these brackets and then check the answers by double clicking on the i reference. (a + b)2= a 2 + 2 ab + b 2 (a + b)3= a 3 + 3 a 2 b + 3 ab 2 + b 3 1/5/2022 Maths @ Paston © P. R. Brayne 8

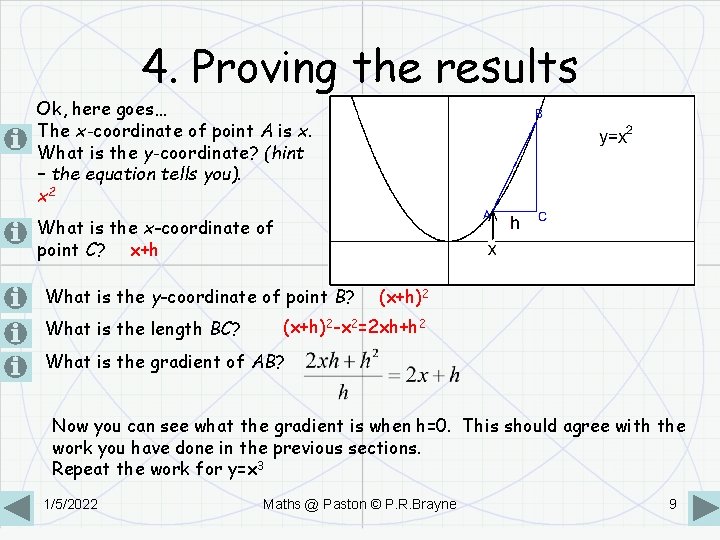
4. Proving the results Ok, here goes… The x-coordinate of point A is x. What is the y-coordinate? (hint – the equation tells you). x 2 What is the x-coordinate of point C? x+h What is the y-coordinate of point B? What is the length BC? (x+h)2 -x 2=2 xh+h 2 What is the gradient of AB? Now you can see what the gradient is when h=0. This should agree with the work you have done in the previous sections. Repeat the work for y=x 3 1/5/2022 Maths @ Paston © P. R. Brayne 9

Possible extension questions Now that you have been through theory you could apply it to these questions 1. What is the gradient function of a multiple of the examples you have done e. g. y=4 x 3 2. What is the gradient function when you add these examples? E. g. y=2 x 3+x 2 3. Can you prove the results for x 3, x 4 etc. using the ideas in section 4 (Look up binomial theorem to help you. 1/5/2022 Maths @ Paston © P. R. Brayne 10