YEAR 1 PROOF Consequence and equivalence Disproof by

YEAR 1 -PROOF Consequence and equivalence Disproof by counter-example Proof by deduction Proof by exhaustion 30/10/2021 1

PROOF | KEY FACTS 30/10/2021 To prove a mathematical statement, we must show that it is true in all possible situations. We will be covering the following methods of proof: Disproof by Counter Example Proof by Deduction Proof by Exhaustion Proof by contradiction (year 2 only) 2

CONSEQUENCE AND EQUIVALENCE • This means if one is true, then the other must be true (but not necessarily the other way) 30/10/2021 3

CONSEQUENCE AND EQUIVALENCE Consider the following two statements: The last digit of a number is a 5. A number is divisible by 5. We can say that: However, we cannot say that: e. g. 10 is divisible by 5, but does not end in a 5. 30/10/2021 4

CONSEQUENCE AND EQUIVALENCE Consider the following two statements: The last digit of a number is a 0. A number is divisible by 10. We can say that: We can also say that Therefore, the two statements are equivalent: 30/10/2021 5

CONSEQUENCE AND EQUIVALENCE | MINI WHITEBOARDS Be prepared to justify your answers. (a) A: B: The triangle has equal sides. The triangle has equal angles ✓/✗ (b) A: B: The equation is linear. The equation has exactly one real root. ✓/✗ (c) A: B: Sam can do 10 push-ups. Sam can do 100 push-ups. ✓/✗ (d) A: B: P and Q are not both true. P and Q are both not true. ✓/✗ 30/10/2021 6

CONSEQUENCE AND EQUIVALENCE 30/10/2021 Quick Examples Line 1 is equivalent to line 2 If line 1 is true, then line 2 is also true (note that the reverse is not true) 7

30/10/2021 EXERCISE 1 A | PAGE 4 |ANSWERS P 530 Q 4, Q 6, Q 7, Q 8, Q 9, Q 10 8

DISPROOF BY COUNTER EXAMPLE 30/10/2021 To disprove a statement by counter example, simply choose an example which shows that the statement is not true. 9

DISPROOF BY COUNTER EXAMPLE | EXAMPLE-PROBLEM PAIR 30/10/2021 10

DISPROOF BY COUNTER EXAMPLE | EXAMPLE-PROBLEM PAIR 30/10/2021 11

DISPROOF BY COUNTER EXAMPLE | EXERCISE 1 C | PAGE 7 |ANSWERS 530 Q 1 -9 30/10/2021 12

PROOF BY DEDUCTION To prove a mathematical statement by deduction, we do the following: We begin with an initial statement or assumptions, which we know to be true. We construct a series of logical steps, which follow from our initial assumptions. We reach a conclusion based on the steps followed. 30/10/2021 13

PROOF BY DEDUCTION Many proofs involve even or odd numbers. We can express even and odd numbers algebraically as follows Concrete Examples 14 can be expressed as 2 x 7 26 can be expressed as 2 x 13 15 can be expressed as 2 x 7+1 30/10/2021 14

PROOF BY DEDUCTION | EXAMPLE-PROBLEM PAIRS 1 E. 30/10/2021 15 Prove that the product of an odd and even number is always even. The product of these two numbers gives If we can pull out a factor of 2, the expression represents an even number. This is a multiple of 2, and is therefore even.

PROOF BY DEDUCTION | EXAMPLE-PROBLEM PAIRS 1 P. 30/10/2021 Prove that the product of two odd numbers is odd. Use the right arrow on your keyboard to show the steps… The product of the two odd numbers is given by This is one more than a multiple of 2, and is therefore odd. 16

PROOF BY DEDUCTION | EXAMPLE-PROBLEM PAIRS Q 1 30/10/2021 Prove that the difference between the squares of two consecutive odd numbers is always a multiple of 8. Use the right arrow on your keyboard to show the steps… This is always multiple of 8. 17

PROOF BY DEDUCTION | EXAMPLE-PROBLEM PAIRS Q 2 30/10/2021 Prove that the sum of the squares of two consecutive odd numbers is 2 more than a multiple of 8. Use the right arrow on your keyboard to show the steps… This is 2 more than a multiple of 8. 18

Y 1 PROOF | RECAP EXERCISE 1 D | PAGE 9 |ANSWERS P 512 Complete all questions. 30/10/2021 19

PROOF BY EXHAUSTION 30/10/2021 To prove a mathematical statement by exhaustion, we need to check that a statement is true for all possibilities. However, this does not necessarily mean checking a statement is true for every single number individually. 20

PROOF BY EXHAUSTION | EXAMPLE-PROBLEM PAIR 2 E. 30/10/2021 21 Prove that 97 is a prime number. Checking divisibility for 2 -96 would be very time consuming. Could we eliminate some possibilities? 1. Try numbers in ascending order 2. We only need to try prime numbers If it’s not prime, we’ve already tried a factor. e. g. no point trying 4 if we’ve tried 2. Factors come in pairs. A factor larger than 9. 8 would have to pair with one smaller than 9. 8

PROOF BY EXHAUSTION | EXAMPLE-PROBLEM PAIR 2 E. 30/10/2021 Prove that 97 is a prime number. Try all prime numbers below 9. 84 There are no factors below 9. 84…. 22

30/10/2021 2 P. Prove that 83 is a prime number. Use the right arrow on your keyboard to show the steps… There are no factors below 9. 11. . . 23

PROOF BY EXHAUSTION | CASE ANALYSIS 30/10/2021 Case analysis is where we break a problem down into all possible small cases and examine each case separately. 24

PROOF BY EXHAUSTION | EXAMPLE-PROBLEM PAIR 3 E. A whole number is squared and divided by 3. Prove that the remainder can only be 0 or 1. A multiple of 3 One more than a multiple of 3 Two more than a multiple of 3 We then consider each case separately. 30/10/2021 25

PROOF BY EXHAUSTION | EXAMPLE-PROBLEM PAIR 3 E. 30/10/2021 A whole number is squared and divided by 3. Prove that the remainder can only be 0 or 1. Case 1: Case 2: Case 3: 26

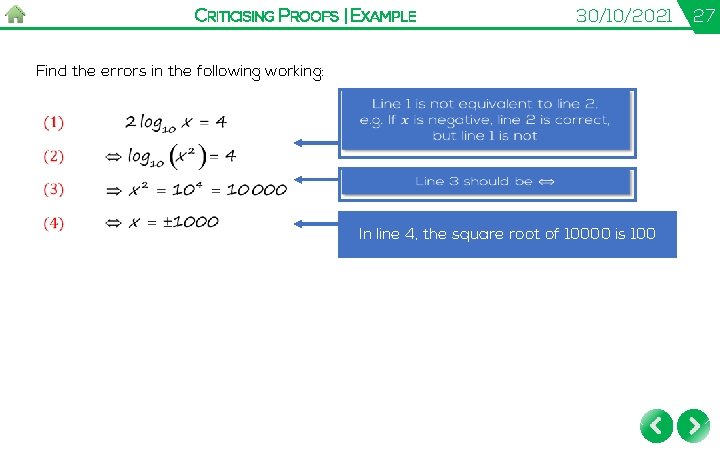
CRITICISING PROOFS | EXAMPLE 30/10/2021 Find the errors in the following working: In line 4, the square root of 10000 is 100 27

CRITICISING PROOFS | EXERCISE 1 C | PAGE 6 |ANSWERS P 512 Q 1 -7 30/10/2021 28

PROOF BY CONTRADICTION 30/10/2021 Proof by contradiction starts from the opposite of a statement you are trying to prove, and shows that this result is an impossible conclusion. There are two key proofs by contradiction that are specifically mentioned in the specification: Proving that there an infinite number of primes. 29

PROOF BY CONTRADICTION | KEY PROOFS 30/10/2021 Use proof by contradiction to prove that there an infinite number of prime numbers. KEY FACTS YOU NEED TO KNOW FIRST… A prime number has only 2 factors – 1 and the number itself. Any number can be written as a product of its prime factors. Notice that this means it is divisible by all of its prime factors. 30

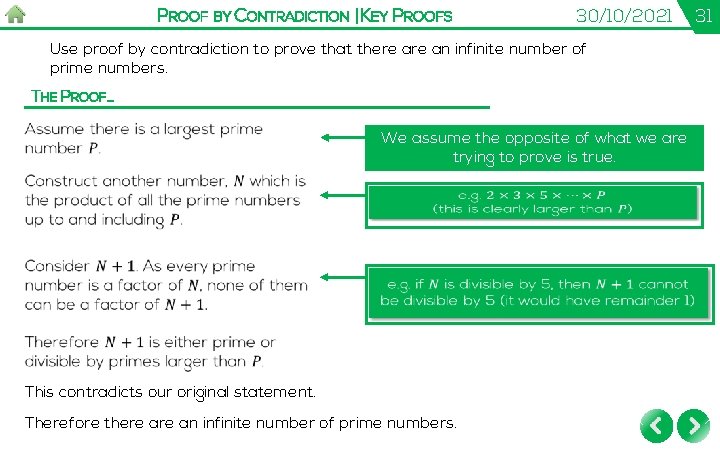
PROOF BY CONTRADICTION | KEY PROOFS 30/10/2021 Use proof by contradiction to prove that there an infinite number of prime numbers. THE PROOF… We assume the opposite of what we are trying to prove is true. This contradicts our original statement. Therefore there an infinite number of prime numbers. 31

PROOF BY CONTRADICTION | KEY PROOFS KEY FACTS YOU NEED TO KNOW FIRST… Proof: 30/10/2021 32

PROOF BY CONTRADICTION | KEY PROOFS 30/10/2021 THE PROOF… A rational number can be expressed as a fraction where both parts are integers. There are no common factors if we write it in its simplest form (we can do this for any fraction). This contradicts our original assertion. 33

CRITICISING PROOFS | EXERCISE 1 B | PAGE 4 |ANSWERS P 512 Q 1 -12 30/10/2021 34