Xray Scattering from Thin Films Experimental methods for

X-ray Scattering from Thin Films Ø Experimental methods for thin films analysis using X-ray scattering – – Ø Conventional XRD diffraction Glancing angle X-ray diffraction X-ray reflectivity measurement Grazing incidence X-ray diffraction study of real structure of thin films – – – Phase analysis Residual stress analysis Crystallite size and strain determination Study of the preferred orientation Study of the crystal anisotropy

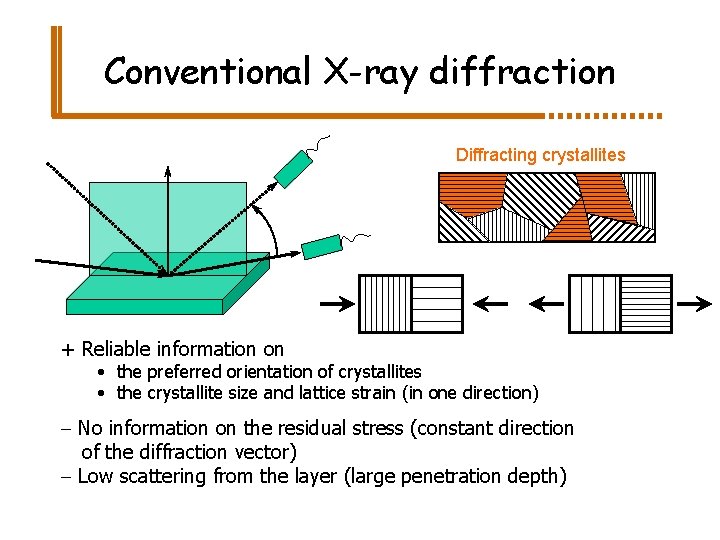
Conventional X-ray diffraction Diffracting crystallites + Reliable information on • the preferred orientation of crystallites • the crystallite size and lattice strain (in one direction) - No information on the residual stress (constant direction of the diffraction vector) - Low scattering from the layer (large penetration depth)

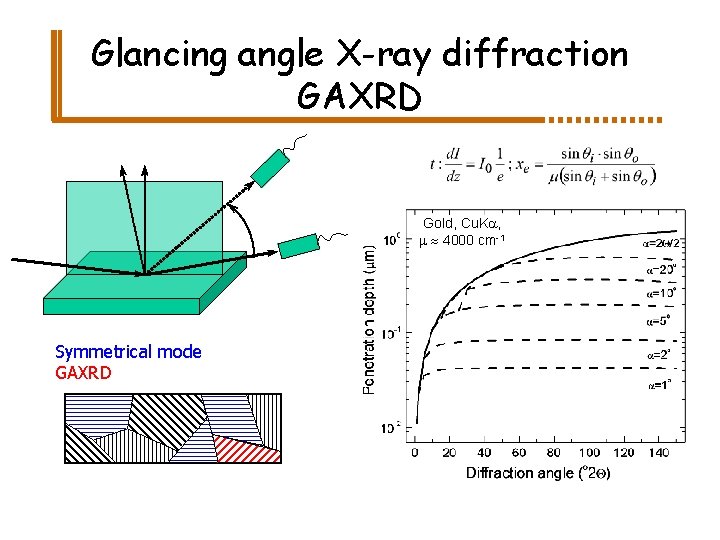
Glancing angle X-ray diffraction GAXRD Gold, Cu. Ka, m 4000 cm-1 Symmetrical mode GAXRD

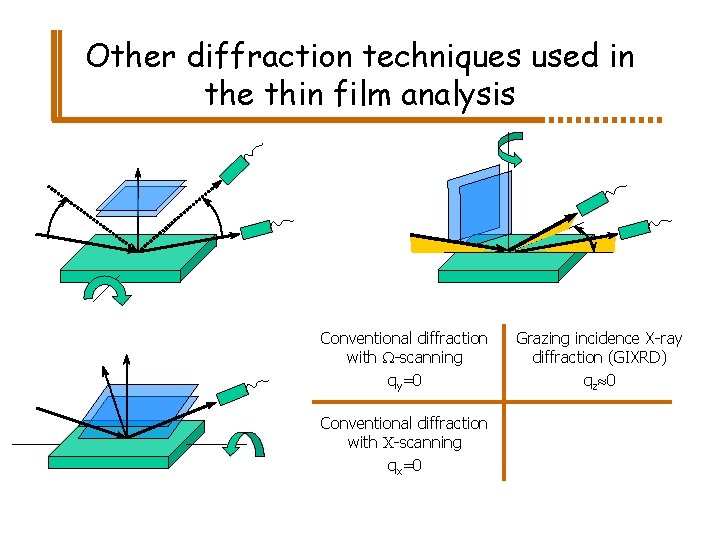
Other diffraction techniques used in the thin film analysis Conventional diffraction with W-scanning qy=0 Conventional diffraction with C-scanning qx=0 Grazing incidence X-ray diffraction (GIXRD) qz 0

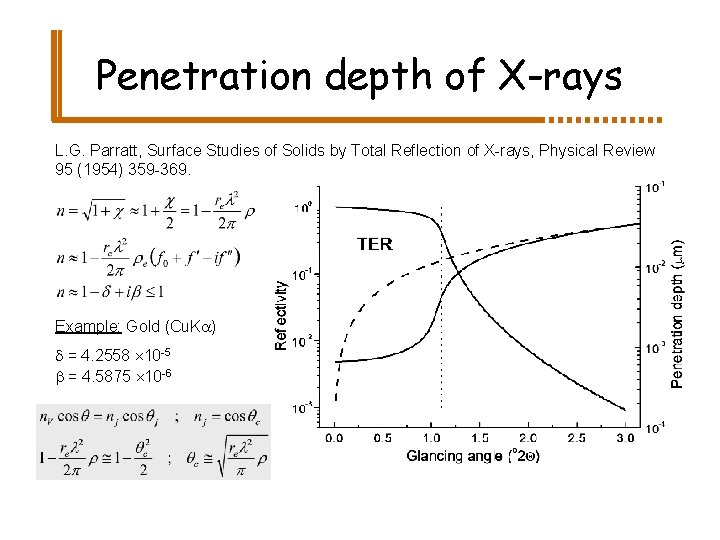
Penetration depth of X-rays L. G. Parratt, Surface Studies of Solids by Total Reflection of X-rays, Physical Review 95 (1954) 359 -369. Example: Gold (Cu. Ka) d = 4. 2558 10 -5 b = 4. 5875 10 -6

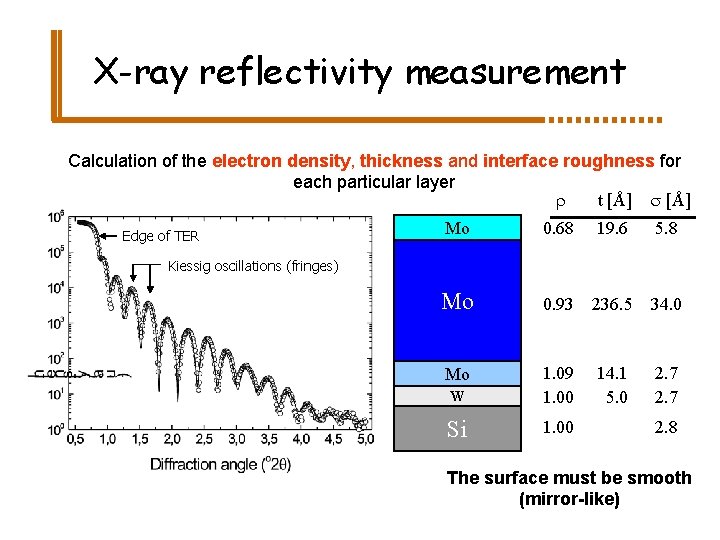
X-ray reflectivity measurement Calculation of the electron density, thickness and interface roughness for each particular layer r t [Å] s [Å] Edge of TER Mo 0. 68 19. 6 5. 8 Mo 0. 93 236. 5 34. 0 Mo W 1. 09 1. 00 14. 1 5. 0 2. 7 Si 1. 00 Kiessig oscillations (fringes) 2. 8 The surface must be smooth (mirror-like)

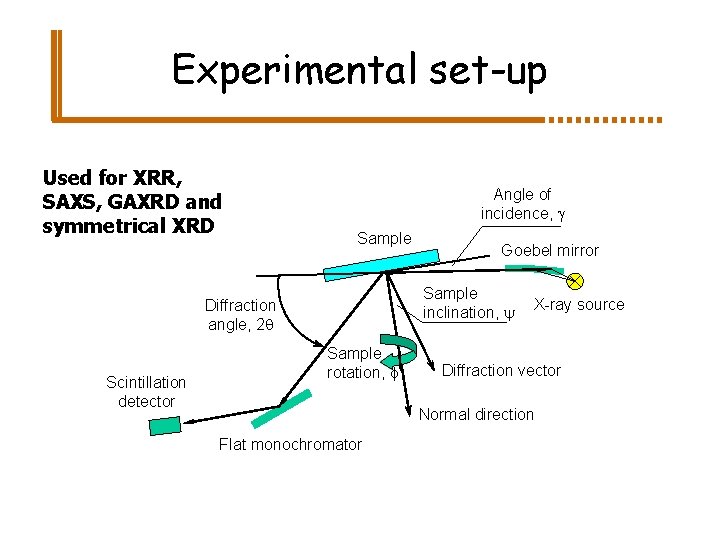
Experimental set-up Used for XRR, SAXS, GAXRD and symmetrical XRD Angle of incidence, g Sample inclination, y Diffraction angle, 2 q Scintillation detector Goebel mirror Sample rotation, f X-ray source Diffraction vector Normal direction Flat monochromator

Information on the microstructure of thin films Ø Phase analysis Ø Residual stress analysis Ø Crystallite size and strain determination Ø Study of the preferred orientation Ø Study of the anisotropy in the lattice deformation Ø Investigation of the depth gradients of microstructure parameters

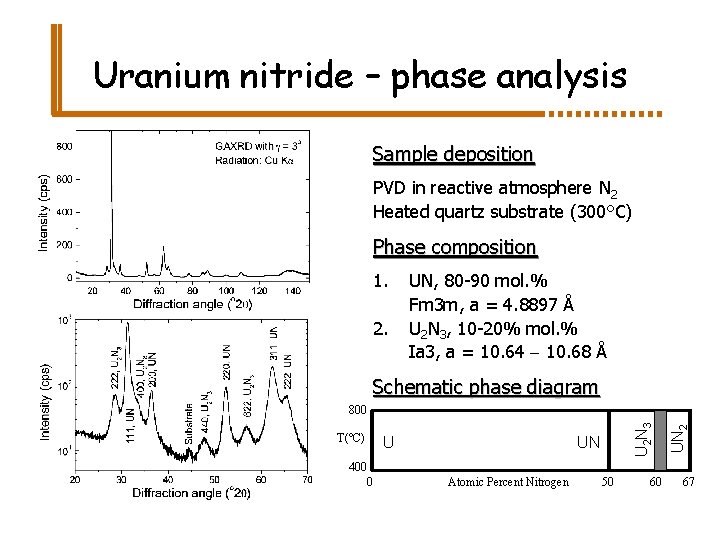
Uranium nitride – phase analysis Sample deposition PVD in reactive atmosphere N 2 Heated quartz substrate (300°C) Phase composition 1. 2. UN, 80 -90 mol. % Fm 3 m, a = 4. 8897 Å U 2 N 3, 10 -20% mol. % Ia 3, a = 10. 64 - 10. 68 Å Schematic phase diagram U UN UN 2 T(°C) U 2 N 3 800 400 0 Atomic Percent Nitrogen 50 60 67

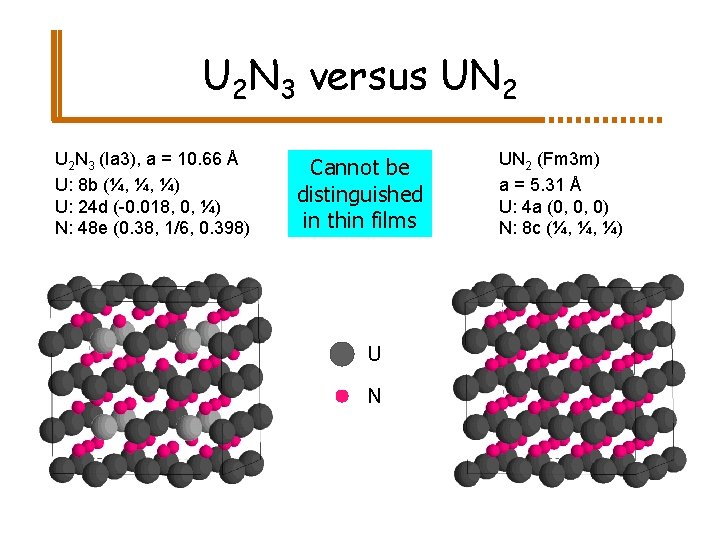
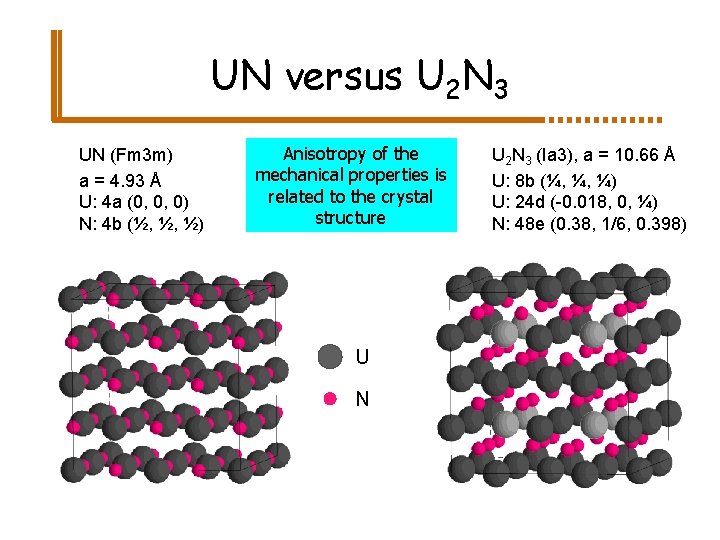
U 2 N 3 versus UN 2 U 2 N 3 (Ia 3), a = 10. 66 Å U: 8 b (¼, ¼, ¼) U: 24 d (-0. 018, 0, ¼) N: 48 e (0. 38, 1/6, 0. 398) Cannot be distinguished in thin films U N UN 2 (Fm 3 m) a = 5. 31 Å U: 4 a (0, 0, 0) N: 8 c (¼, ¼, ¼)

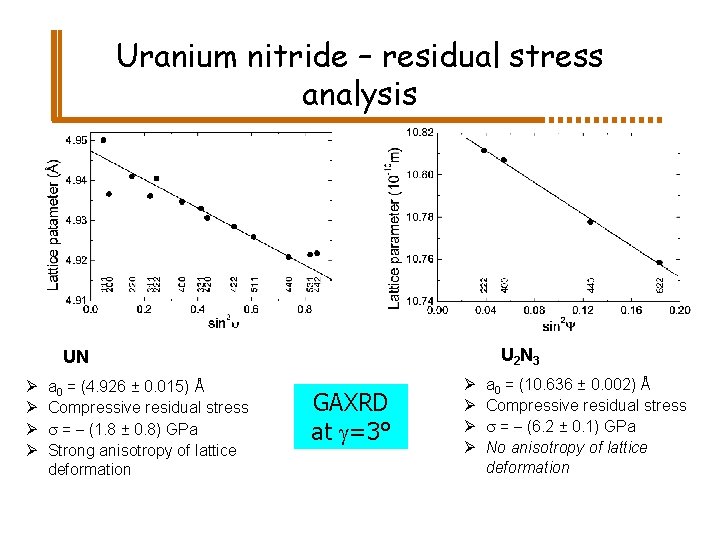
Uranium nitride – residual stress analysis U 2 N 3 UN Ø Ø a 0 = (4. 926 ± 0. 015) Å Compressive residual stress s = - (1. 8 ± 0. 8) GPa Strong anisotropy of lattice deformation GAXRD at g=3° Ø Ø a 0 = (10. 636 ± 0. 002) Å Compressive residual stress s = - (6. 2 ± 0. 1) GPa No anisotropy of lattice deformation

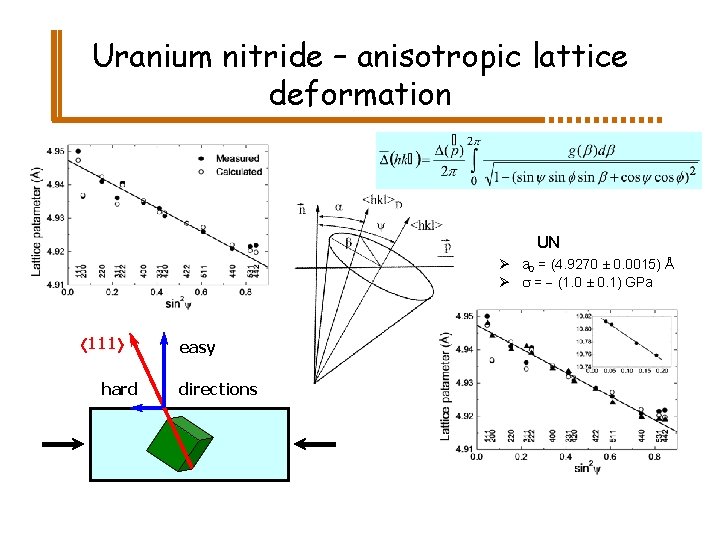
Uranium nitride – anisotropic lattice deformation UN Ø a 0 = (4. 9270 ± 0. 0015) Å Ø s = - (1. 0 ± 0. 1) GPa 111 hard easy directions

UN – anisotropic lattice deformation Dependence of the lattice deformation on the crystallographic direction R. W. Vook and F. Witt, J. Appl. Phys. , 36 (1965) 2169. Related to the anisotropy of the elastic constants

UN versus U 2 N 3 UN (Fm 3 m) a = 4. 93 Å U: 4 a (0, 0, 0) N: 4 b (½, ½, ½) Anisotropy of the mechanical properties is related to the crystal structure U N U 2 N 3 (Ia 3), a = 10. 66 Å U: 8 b (¼, ¼, ¼) U: 24 d (-0. 018, 0, ¼) N: 48 e (0. 38, 1/6, 0. 398)

Methods for the size-strain analysis using XRD Crystallite size Lattice strain Ø Fourier transformation of finite objects (with limited size) Ø Constant line broadening (with increasing diffraction vector) Ø Local changes in the d-spacing Ø Line broadening increases with increasing q (a result of the Bragg equation in the differential form) (011) (111) (001) (110) (000) Scherrer (100) Williamson-Hall P. Klimanek (Freiberg) R. Kuzel (Prague) (110) (000) Warren-Averbach P. Scardi (Trento) (100) Krivoglaz T. Ungar (Budapest)

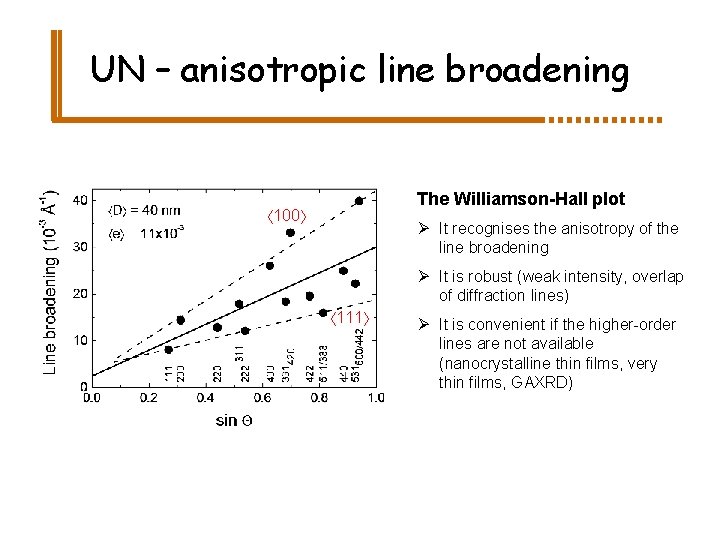
UN – anisotropic line broadening The Williamson-Hall plot 100 Ø It recognises the anisotropy of the line broadening Ø It is robust (weak intensity, overlap of diffraction lines) 111 Ø It is convenient if the higher-order lines are not available (nanocrystalline thin films, very thin films, GAXRD)

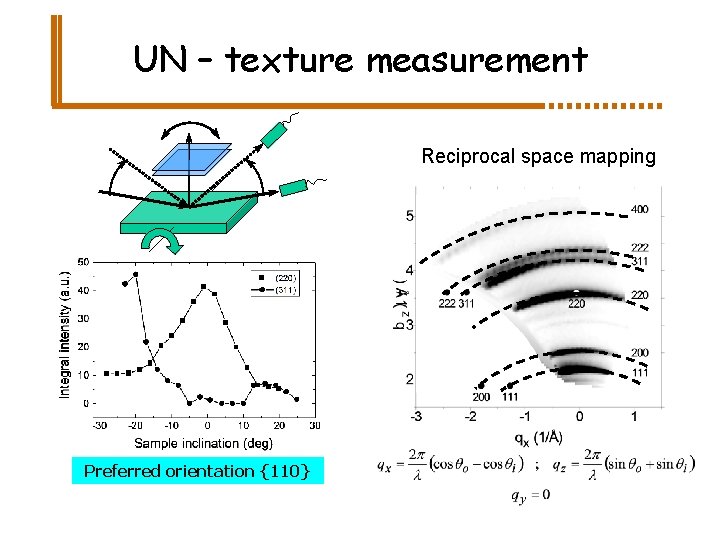
UN – texture measurement Reciprocal space mapping Preferred orientation {110}

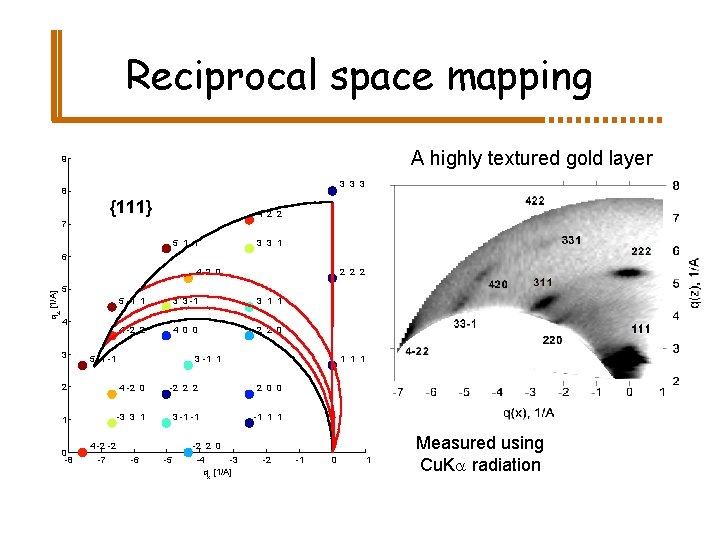
Reciprocal space mapping A highly textured gold layer 9 3 3 3 8 {111} 4 2 2 7 5 1 1 3 3 1 6 qz [1/A] 4 2 0 2 2 2 5 4 3 5 -1 1 3 3 -1 3 1 1 4 -2 2 4 0 0 2 2 0 5 -1 -1 3 -1 1 1 2 4 -2 0 -2 2 0 0 1 -3 3 1 3 -1 -1 -1 1 1 0 -8 4 -2 -2 -7 -2 2 0 -6 -5 -4 -3 qx [1/A] -2 -1 0 1 Measured using Cu. Ka radiation

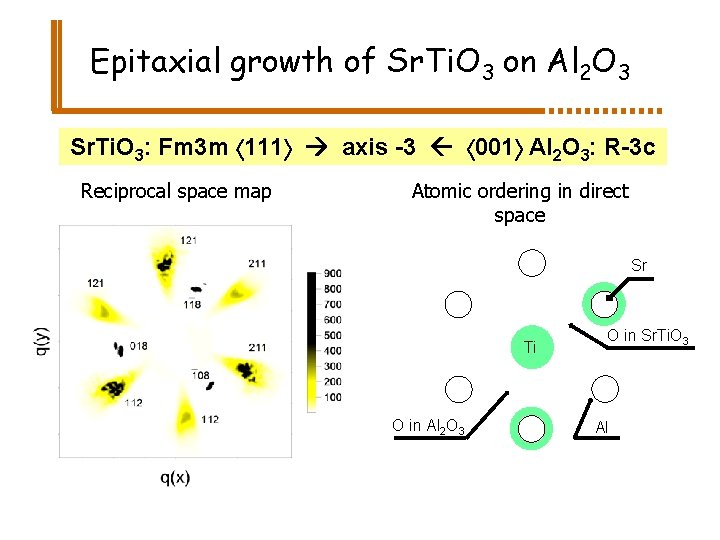
Epitaxial growth of Sr. Ti. O 3 on Al 2 O 3 Sr. Ti. O 3: Fm 3 m 111 axis -3 001 Al 2 O 3: R-3 c Reciprocal space map Atomic ordering in direct space Sr Ti O in Al 2 O 3 O in Sr. Ti. O 3 Al

Sr. Ti. O 3 on Al 2 O 3 Atomic Force Microscopy Pyramidal crystallites with two different in-plane orientations 111 _ 110 AFM micrograph courtesy of Dr. J. Lindner, Aixtron AG, Aachen.

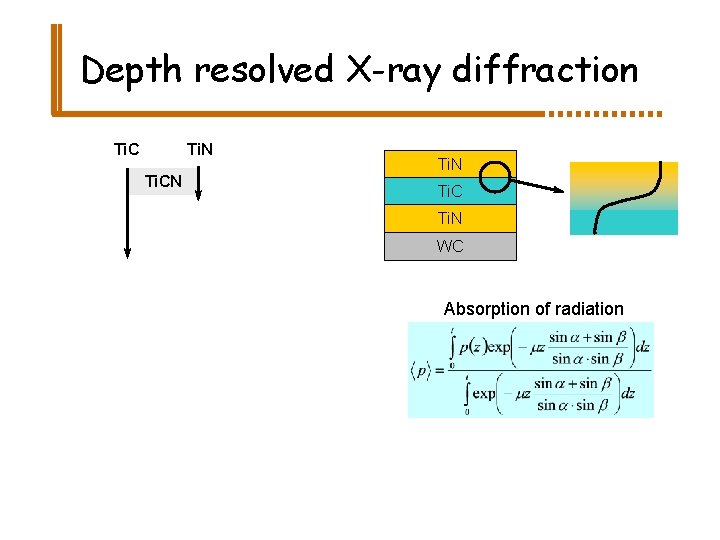
Depth resolved X-ray diffraction Ti. N Ti. CN Ti. C Ti. N WC Absorption of radiation

Surface modification of thin films Gradient of the residual stress in thin Ti. N coatings (CVD) implanted by metal ions: Y, Mo, W, Al and Cr

Functionally graded materials W. Lengauer and K. Dreyer, J. Alloys Comp. 338 (2002) 194 Nitrogen – in-diffusion from N 2 N-rich zone of (Ti, W)(C, N) Ti(C, N) N-poor zone of (Ti, W)(C, N) (Ti, W)C SEM micrograph courtesy of C. Kral, Vienna University of Technology, Austria

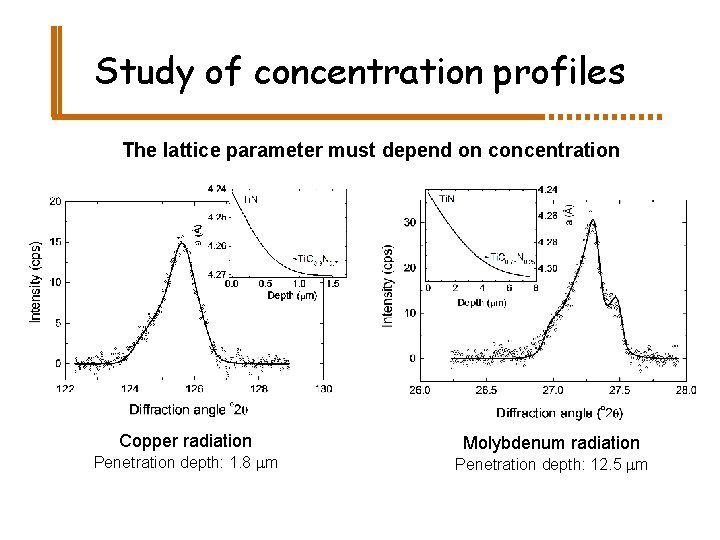
Study of concentration profiles The lattice parameter must depend on concentration Copper radiation Penetration depth: 1. 8 mm Molybdenum radiation Penetration depth: 12. 5 mm

Summary Benefits of X-ray scattering. . . for investigation of the real structure of thin films Length scale between 10 -2Å and 103Å is accessible (from atomic resolution to the layer thickness) Ø Small and variable penetration depth of X-ray into the solids (surface diffraction, study of the depth gradients) Ø Easy preparation of samples, non-destructive testing Ø Integral measurement (over the whole irradiated area) Ø