Xray Diffraction and EBSD Jonathan Cowen Swagelok Center

X-ray Diffraction and EBSD Jonathan Cowen Swagelok Center for the Surface Analysis of Materials Case School of Engineering Case Western Reserve University October 27, 2014

Outline • X-ray Diffraction (XRD) • History and background • Introduction to XRD • Practical applications • Electron Back-Scattered Diffraction (EBSD) • Introduction to EBSD • Types of information that can be drawn from EBSD

Discovery of X-rays and Modern XRD • Wilhelm Conrad Röntgen – 1895: Discovery of X-ray – 1901: awarded first Nobel prize winner for Physics • M. T. F. von Laue: – 1912: Discovery of the diffraction of X-rays by single crystals , in cooperation with Friedrich and Knipping – Terms: Laue equation, Laue reflections – 1914: Nobel prize for Physics • W. H. and W. L. Bragg: – 1914: X-ray diffraction and Crystal Structure – Terms: Bragg‘s equation, Bragg reflections – 1915: Nobel prize for Physics

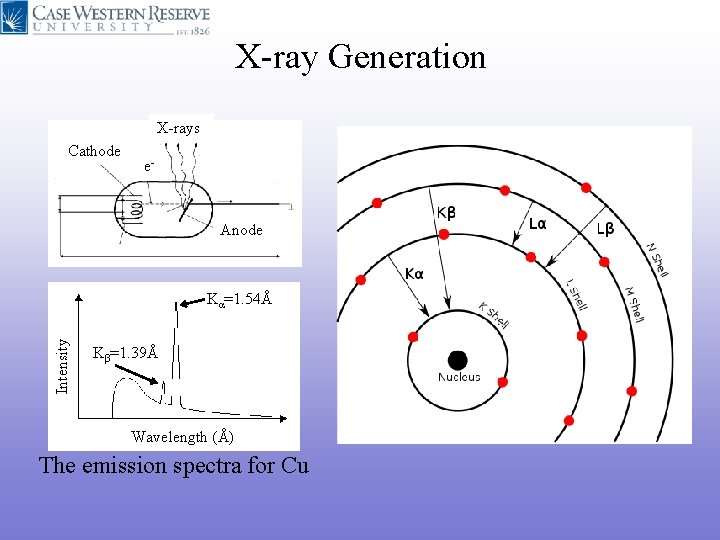
X-ray Generation X-rays Cathode e- Anode Intensity Kα=1. 54Å Kβ=1. 39Å Wavelength (Å) The emission spectra for Cu

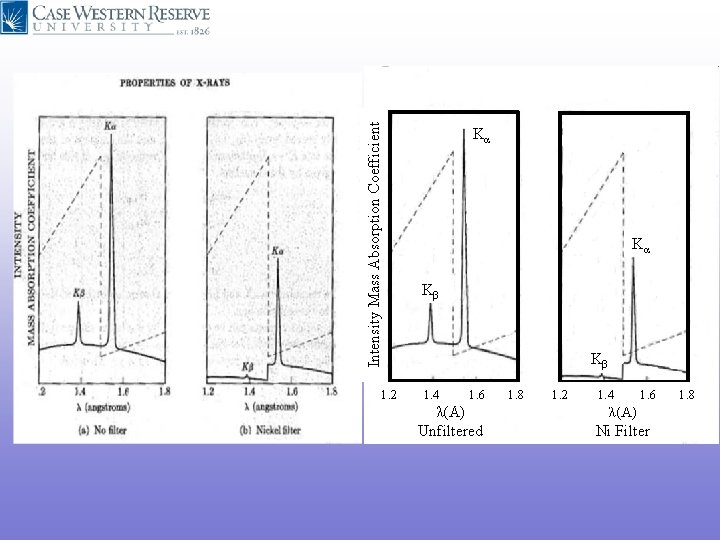
Intensity Mass Absorption Coefficient 1. 2 Monochromatic Radiation is needed for Crystal Structure Analysis Kα Kα Kβ Filters for Suppression of Kβ Radiation Kβ 1. 4 1. 6 λ(Å) Unfiltered 1. 8 1. 2 1. 4 1. 6 1. 8 λ(Å) Ni Filter The dotted line is the Mass Absorption coefficient for Ni

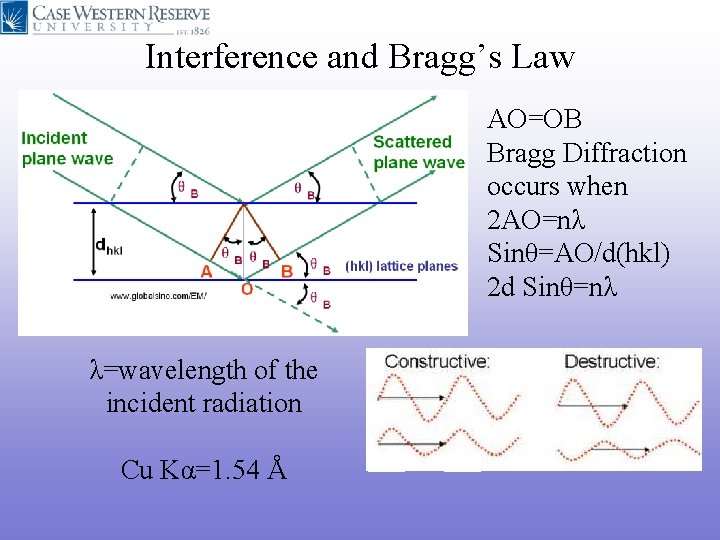
Interference and Bragg’s Law AO=OB Bragg Diffraction occurs when 2 AO=nλ Sinθ=AO/d(hkl) 2 d Sinθ=nλ λ=wavelength of the incident radiation Cu Kα=1. 54 Å

Monochromatic X-rays using Diffraction Graphite monochromator utilizes a highly orientated pyrolytic graphite crystal (HOPG) mounted in a compact metal housing to provide monochromatic radiation. This is usually an improvement over filters. C (Graphite)

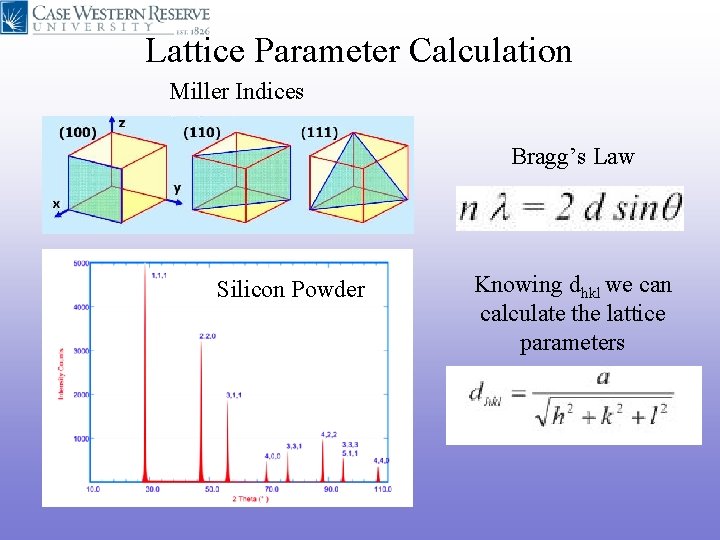
Lattice Parameter Calculation Miller Indices Bragg’s Law Silicon Powder Knowing dhkl we can calculate the lattice parameters

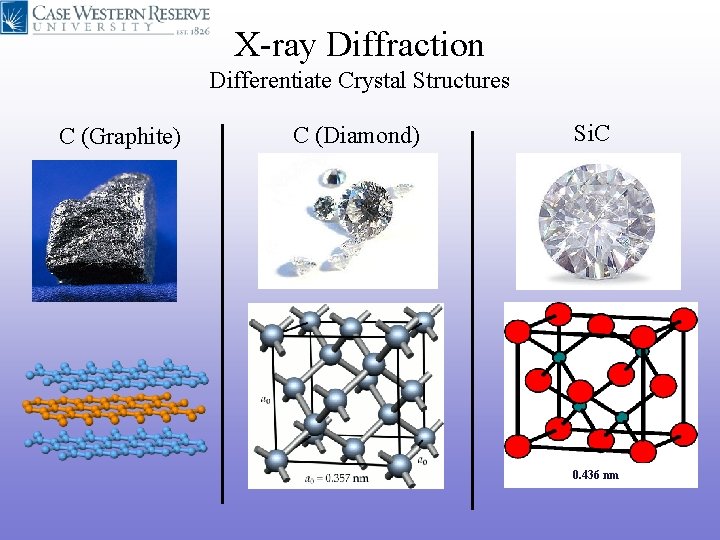
X-ray Diffraction Differentiate Crystal Structures C (Graphite) C (Diamond) Si. C 0. 436 nm

Scintag Advanced X-Ray Diffractometer System Conventional theta-theta scan Rocking curves and sample-tilting curves Grazing angle X-ray diffraction (GAXRD) DMSNT software package is used to control the diffractometer, to acquire raw data and to analyze data. PDF-2 database and searching software for identifying phases

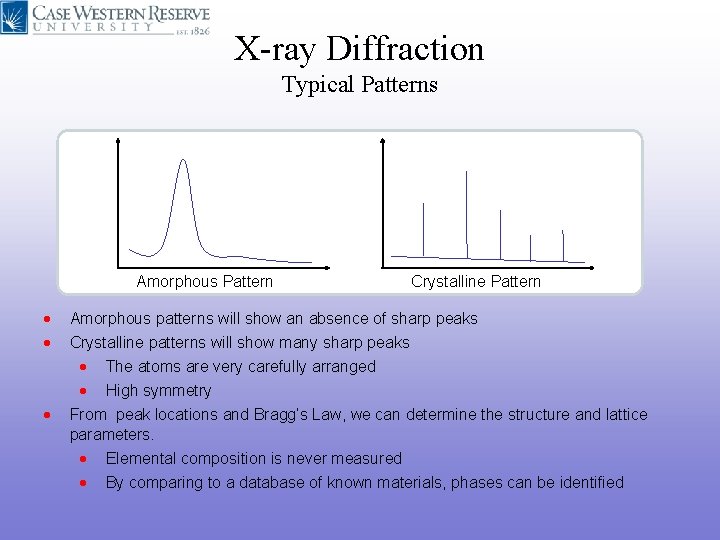
X-ray Diffraction Typical Patterns Amorphous Pattern • • • Crystalline Pattern Amorphous patterns will show an absence of sharp peaks Crystalline patterns will show many sharp peaks • The atoms are very carefully arranged • High symmetry From peak locations and Bragg’s Law, we can determine the structure and lattice parameters. • Elemental composition is never measured • By comparing to a database of known materials, phases can be identified

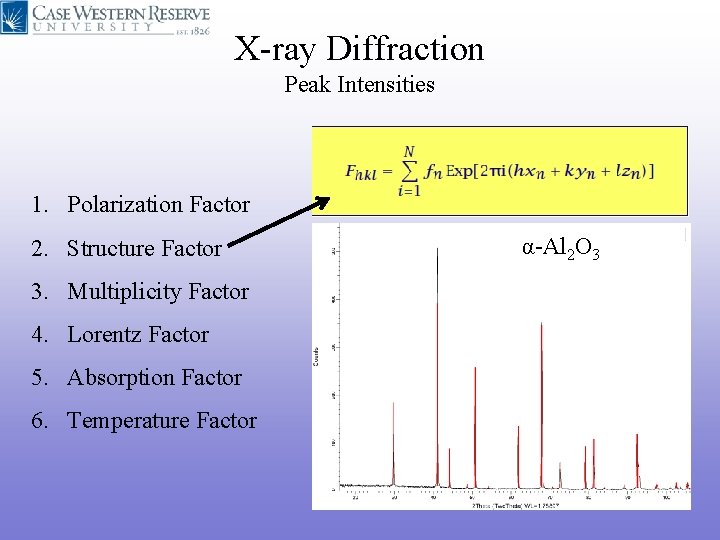
X-ray Diffraction Peak Intensities 1. Polarization Factor 2. Structure Factor 3. Multiplicity Factor 4. Lorentz Factor 5. Absorption Factor 6. Temperature Factor α-Al 2 O 3

X-ray Diffraction Phase Identification International Centre for Diffraction Data (ICDD) Iron Chloride Dihydrate • The PDF-2 (Powder Diffraction File) database contains over 265 K entries. • Modern computer programs can determine what phases are present in any sample by quickly comparing the diffraction data to all of the patterns in the database. • The PDF card for an entry contains much useful information, including literature references.

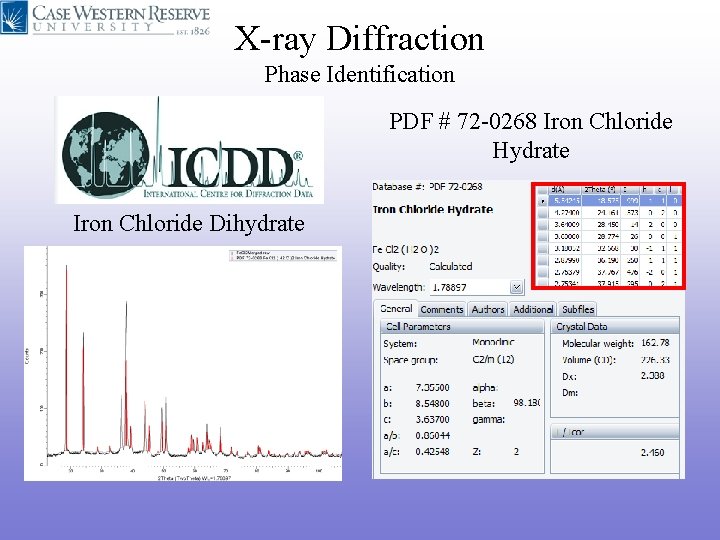
X-ray Diffraction Phase Identification PDF # 72 -0268 Iron Chloride Hydrate Iron Chloride Dihydrate

X-ray Diffraction Quantitative Phase Analysis (QPA) • External standard method • A reflection from a pure component. • Direct comparison method • A reflection from another phase within the mixture. • Internal standard method • A reflection from a foreign material mixed within the sample. • Reference Intensity Ratio (RIR) • Generalized internal standard method developed by the ICDD. Breakdown of the PDF-2 database

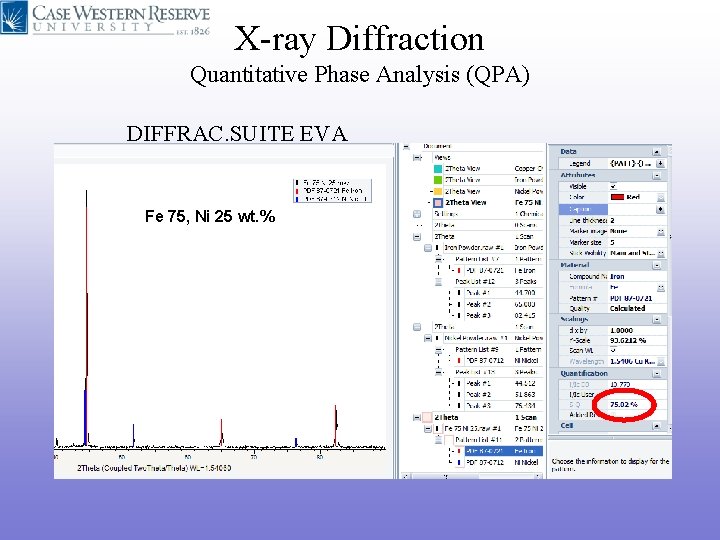
X-ray Diffraction Quantitative Phase Analysis (QPA) DIFFRAC. SUITE EVA Fe 75, Ni 25 wt. %

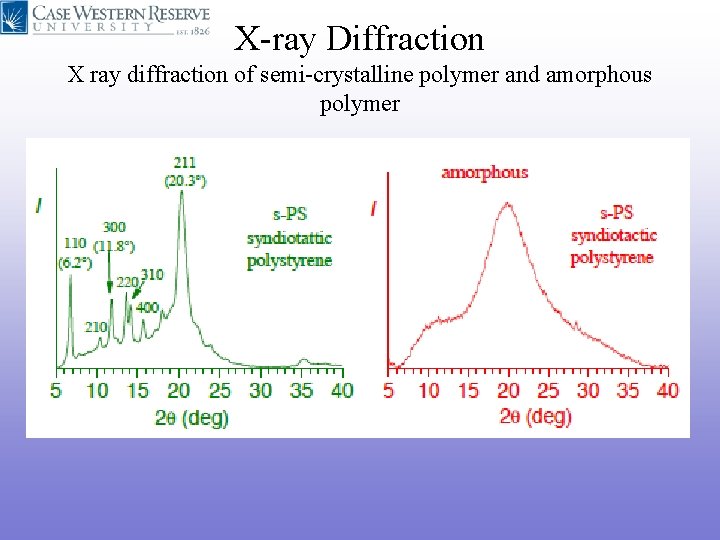
X-ray Diffraction X ray diffraction of semi-crystalline polymer and amorphous polymer

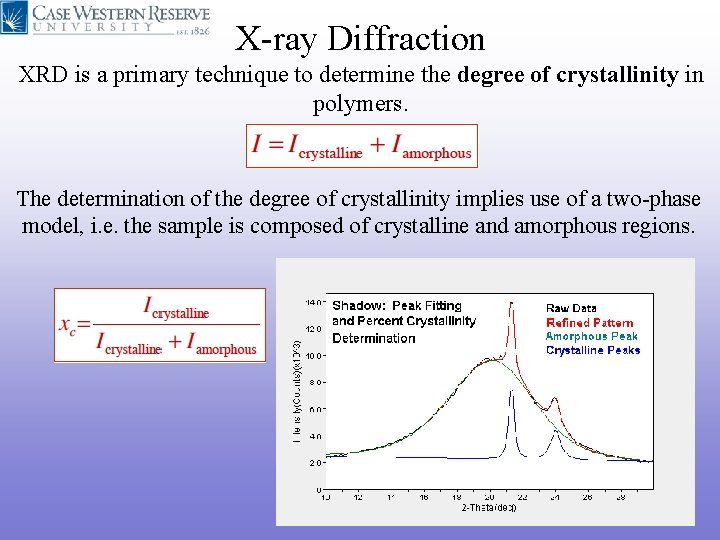
X-ray Diffraction XRD is a primary technique to determine the degree of crystallinity in polymers. The determination of the degree of crystallinity implies use of a two-phase model, i. e. the sample is composed of crystalline and amorphous regions.

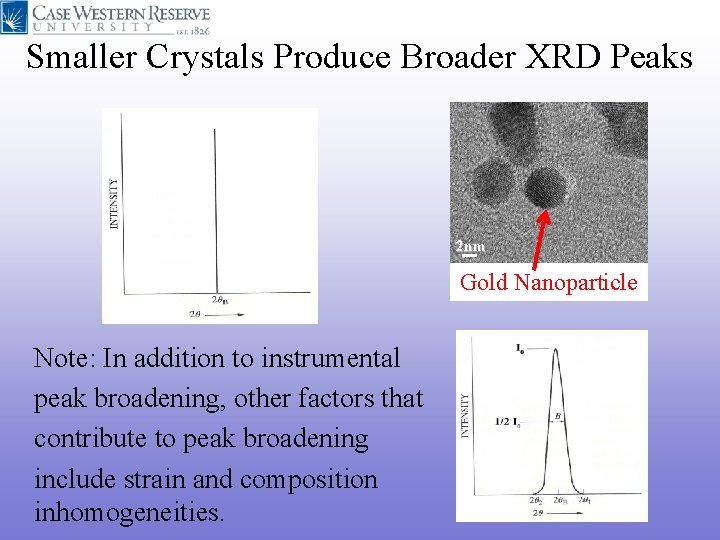
Smaller Crystals Produce Broader XRD Peaks 2 nm Gold Nanoparticle Note: In addition to instrumental peak broadening, other factors that contribute to peak broadening include strain and composition inhomogeneities.

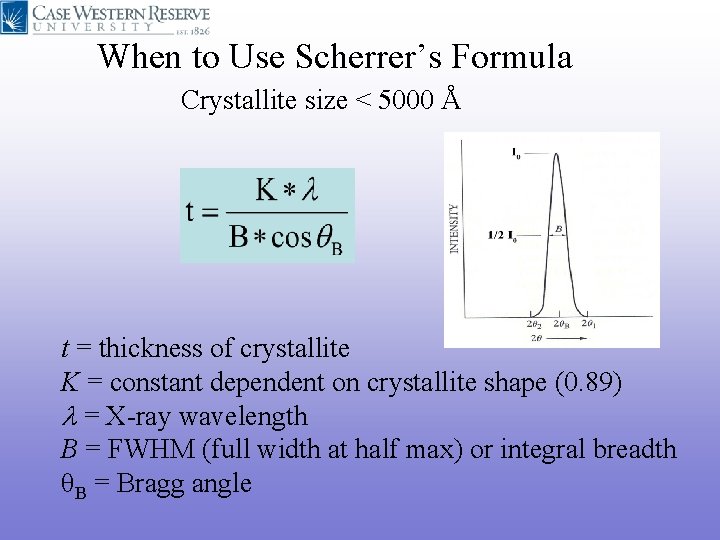
When to Use Scherrer’s Formula Crystallite size < 5000 Å t = thickness of crystallite K = constant dependent on crystallite shape (0. 89) l = X-ray wavelength B = FWHM (full width at half max) or integral breadth θB = Bragg angle

Residual Stress Measurements using X-Ray Diffraction

X-ray Diffraction cones arise from randomly oriented polycrystalline aggregates or powders X-ray Polycrystalline Sample Diffraction Cone forms Debye Rings

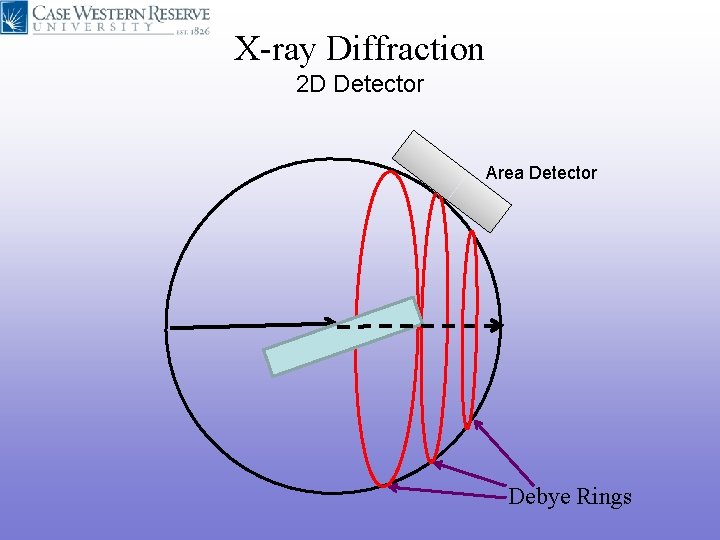
X-ray Diffraction 2 D Detector Area Detector Debye Rings

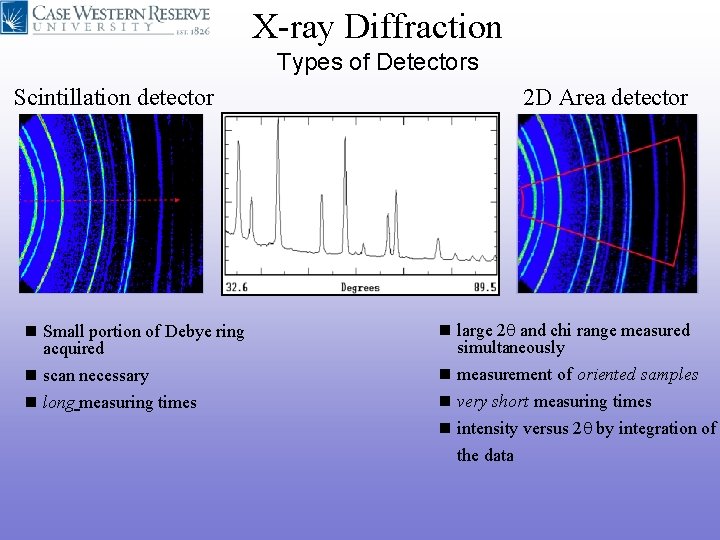
X-ray Diffraction Types of Detectors 2 D Area detector Scintillation detector n Small portion of Debye ring n large 2 and chi range measured n scan necessary n measurement of oriented samples n long measuring times n very short measuring times acquired simultaneously n intensity versus 2 by integration of the data

X-ray Diffraction Bruker D 8 Discover • Small Beam diameter • Can achieve 200μm • Parallel Illumination • Forgives displacement errors • 4 circle Huber goniometer • Dual beam alignment system

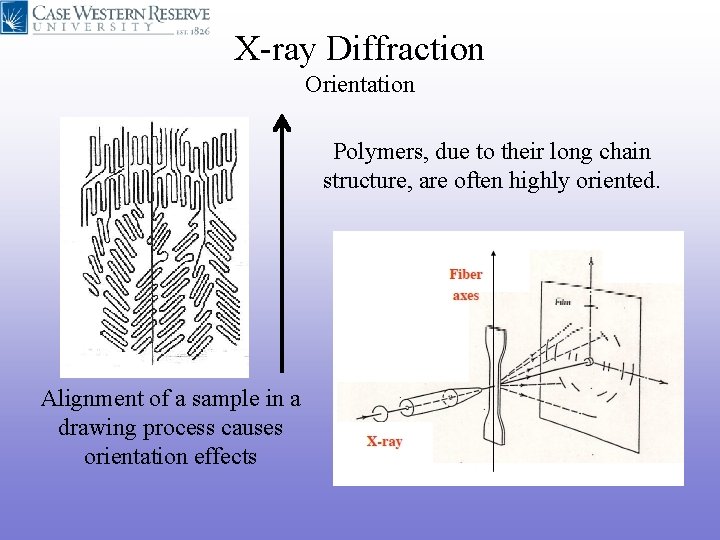
X-ray Diffraction Orientation Polymers, due to their long chain structure, are often highly oriented. Alignment of a sample in a drawing process causes orientation effects

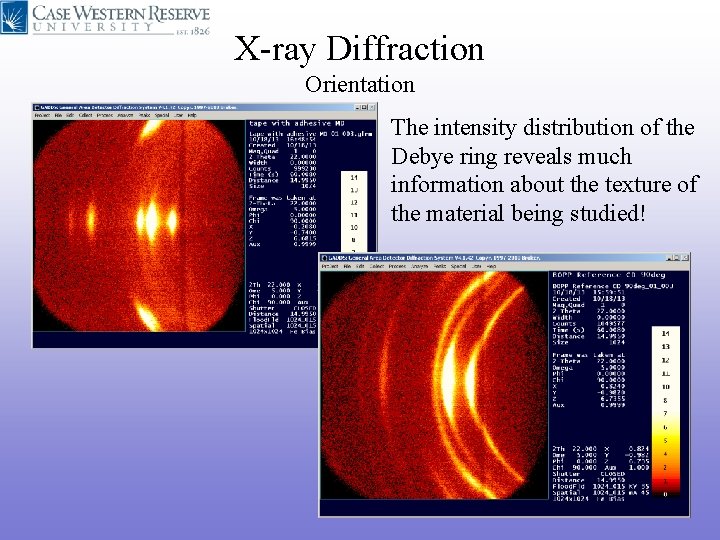
X-ray Diffraction Orientation The intensity distribution of the Debye ring reveals much information about the texture of the material being studied!

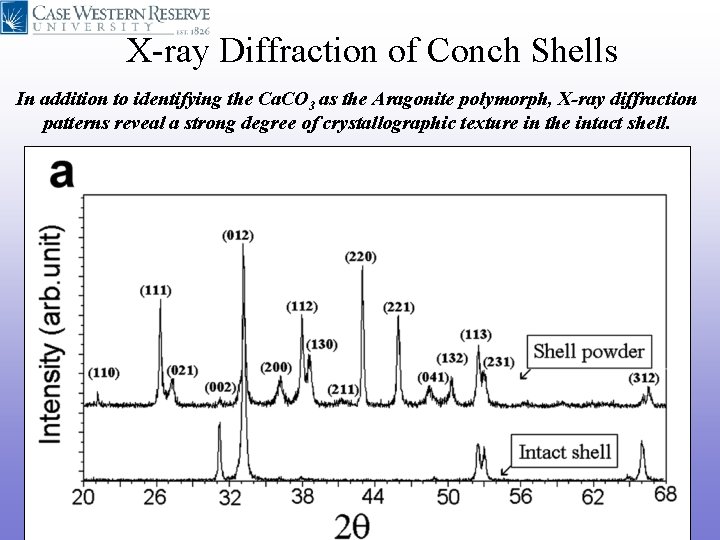
X-ray Diffraction of Conch Shells In addition to identifying the Ca. CO 3 as the Aragonite polymorph, X-ray diffraction patterns reveal a strong degree of crystallographic texture in the intact shell.

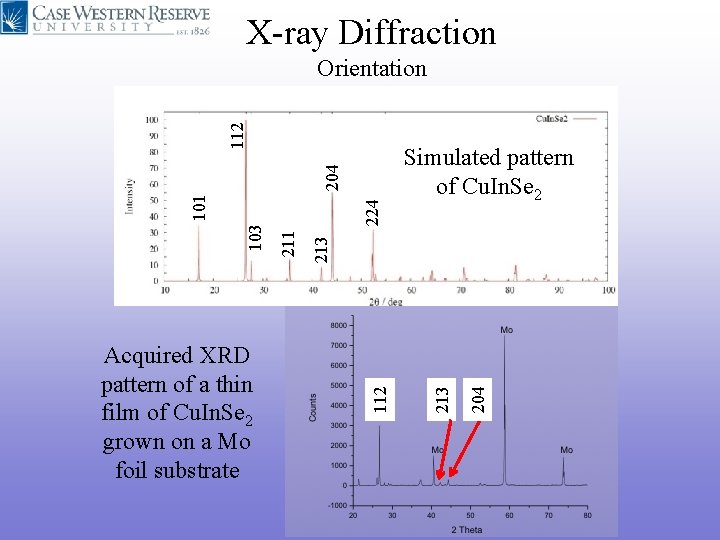
X-ray Diffraction 224 Simulated pattern of Cu. In. Se 2 204 213 112 Acquired XRD pattern of a thin film of Cu. In. Se 2 grown on a Mo foil substrate 211 103 101 204 112 Orientation

X-ray Sources Rigaku D/MAX 2200 Diffractometer Anode Ka 1(Å) Comments Best for inorganics. Fe and Co fluorescence. Cu 1. 54060 Cr High Resolution for large d 2. 28970 spacing. High attenuation in air. Co 1. 78897 Used for ferrous alloys to reduce Fe fluorescence.

X-ray Diffraction Summary • • Structure Determination Phase Identification Quantitative Phase Analysis (QPA) Percent Crystallinity Crystallite Size and Microstrain Residual Stress Measurements (Macrostrain) Texture Analysis Single Crystal Studies (not a SCSAM core competency)

Electron Diffraction Zeiss Libra 200 EF Polycrystal Single Crystal

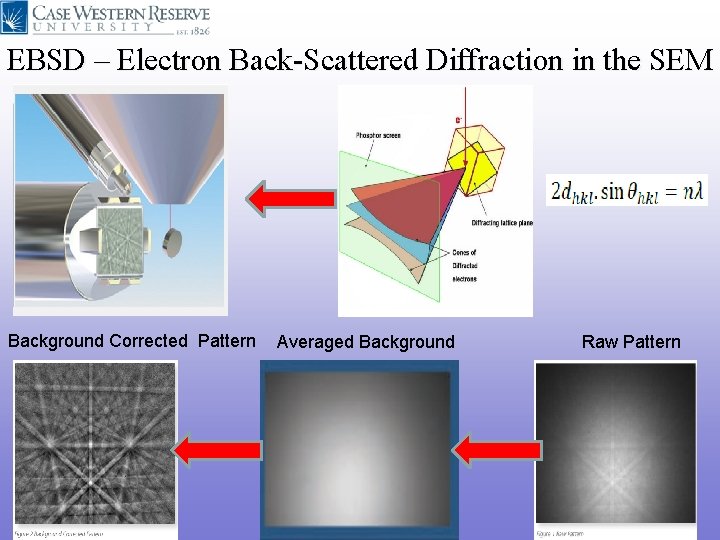
EBSD – Electron Back-Scattered Diffraction in the SEM Background Corrected Pattern Averaged Background Raw Pattern

EBSD – Electron Back-Scattered Diffraction in the SEM Background Corrected Pattern Indexed Pattern 4 12 2 10 1

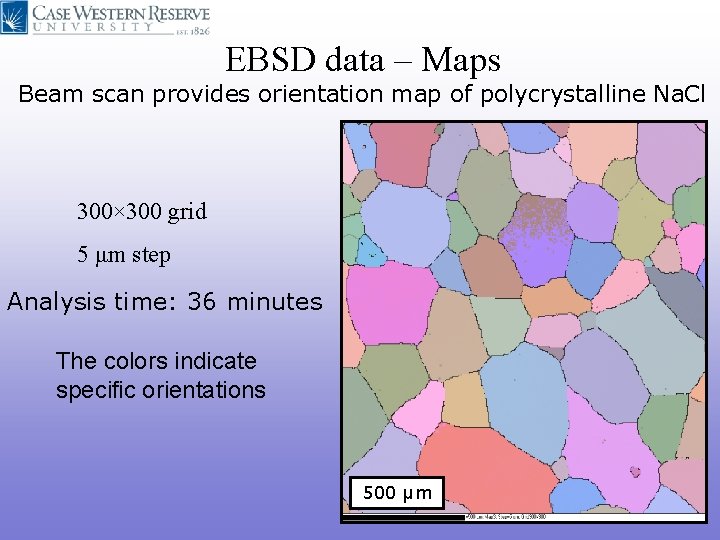
EBSD data – Maps Beam scan provides orientation map of polycrystalline Na. Cl 300× 300 grid 5 μm step Analysis time: 36 minutes The colors indicate specific orientations 500 μm

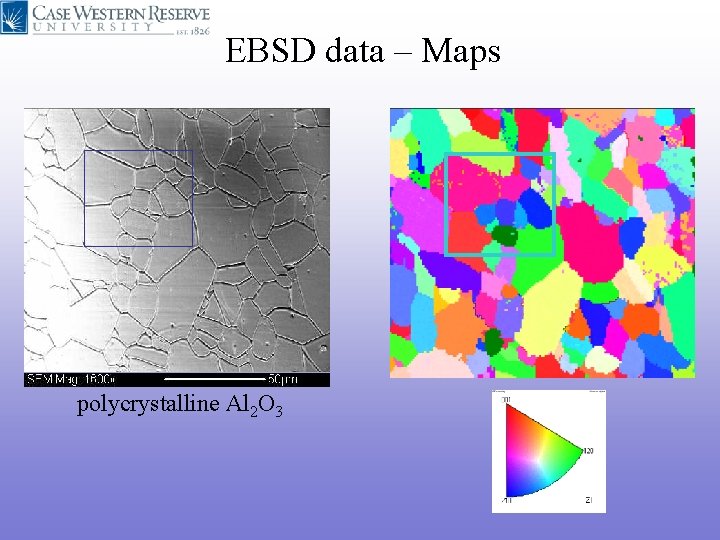
EBSD data – Maps polycrystalline Al 2 O 3

A single automated EBSD run can provide a complete characterization of the microstructure: • • Phase distribution Texture strength Grain size Boundary properties Misorientation data Slip system activity Intra-granular deformation Can collect XEDS simultaneously

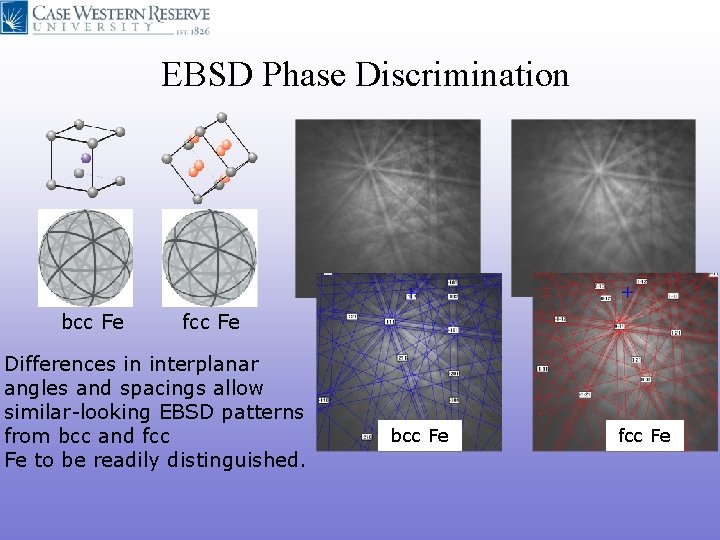
EBSD Phase Discrimination bcc Fe fcc Fe Differences in interplanar angles and spacings allow similar-looking EBSD patterns from bcc and fcc Fe to be readily distinguished. bcc Fe fcc Fe

EBSD data – Maps Phase distribution, texture, grain size / shape, boundary properties, misorientation, slip system activity, intra-granular deformation. . Phase map Orientation bcc Orientation fcc

Summary • XRD is a powerful tool for answering some specific questions about a given sample. – Phases present, QPA, orientation, residual stress, texturing, and crystallite size analysis. • XRD is extremely efficient for the characterization of samples. – Sample preparation time is minimal when compared to SEM/EBSD and TEM. – Data acquisition is straight forward and short set up times are required. • XRD will provide a larger sampling area and a more accurate averaged result of the lattice parameter, but EBSD will be more site specific. • EBSD yields similar results and all the same “specific questions” can be answered in one data set!

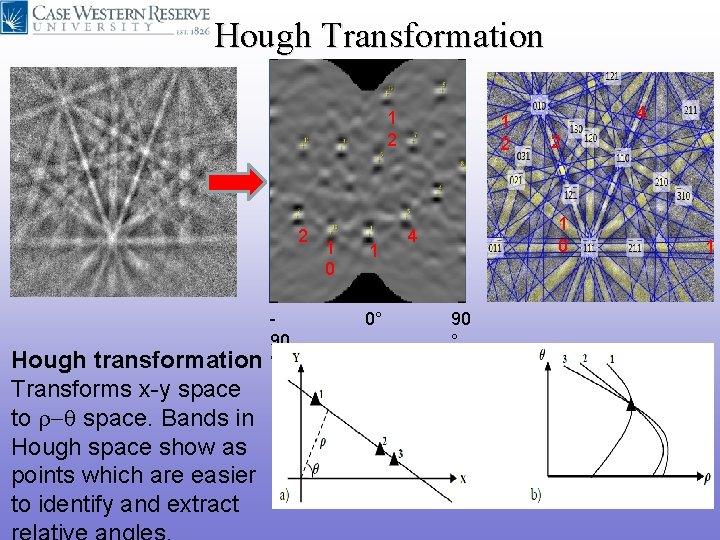
Hough Transformation 1 2 2 Hough transformation Transforms x-y space to r- space. Bands in Hough space show as points which are easier to identify and extract 90 ° 1 0° 1 2 4 2 1 0 4 90 ° 1

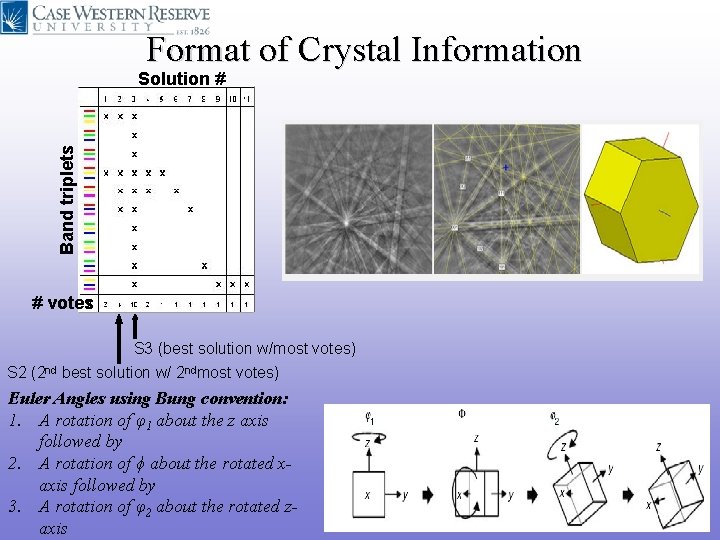
Format of Crystal Information Band triplets Solution # # votes S 3 (best solution w/most votes) S 2 (2 nd best solution w/ 2 ndmost votes) Euler Angles using Bung convention: 1. A rotation of φ1 about the z axis followed by 2. A rotation of ϕ about the rotated xaxis followed by 3. A rotation of φ2 about the rotated zaxis

X-ray Diffraction Phase Identification

Intensity Mass Absorption Coefficient 1. 2 Kα Kα Kβ Kβ 1. 4 1. 6 λ(Å) Unfiltered 1. 8 1. 2 1. 4 1. 6 λ(Å) Ni Filter 1. 8