XRay Computed Tomography Radon Transform Fourier Slice Theorem

X-Ray Computed Tomography • Radon Transform • Fourier Slice Theorem • Backprojection Operator • Filtered Backprojection (FBP) Algorithm • Implementation Issues • Total Variation Reconstruction IPIM, IST, José Bioucas, 2007 1

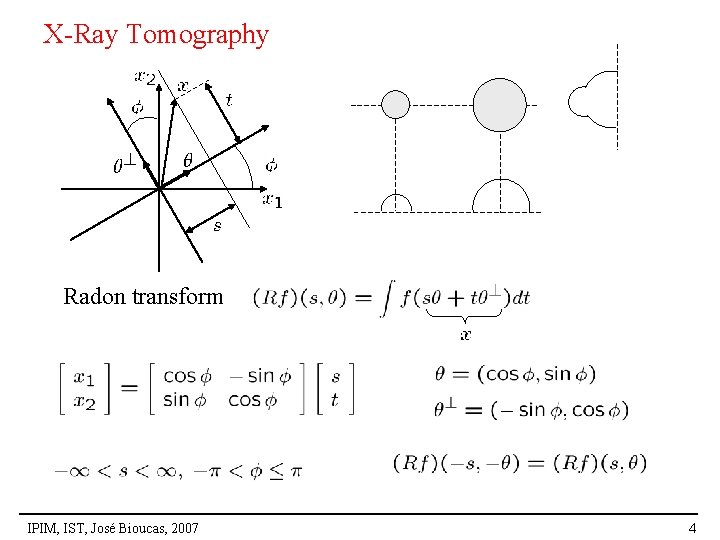
X-Ray Tomography q “Tomography” comes from Greek and means cross-sectional representations of a 3 D object q X-ray tomography, introduced by Hounsfield in 1971, is usually called computed tomography (CT) q CT produces images of human anatonomy with a resolution of about 1 mm and an attenuation coefficient attenuation of about 1% S L body dl R IPIM, IST, José Bioucas, 2007 2

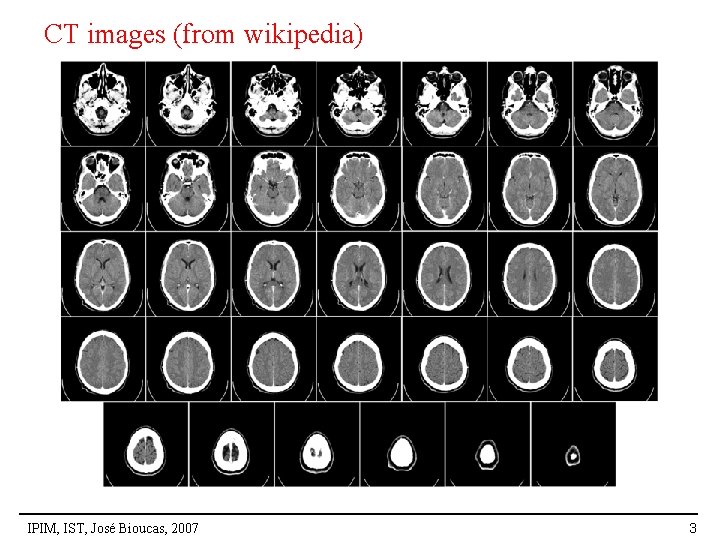
CT images (from wikipedia) IPIM, IST, José Bioucas, 2007 3

X-Ray Tomography Radon transform IPIM, IST, José Bioucas, 2007 4

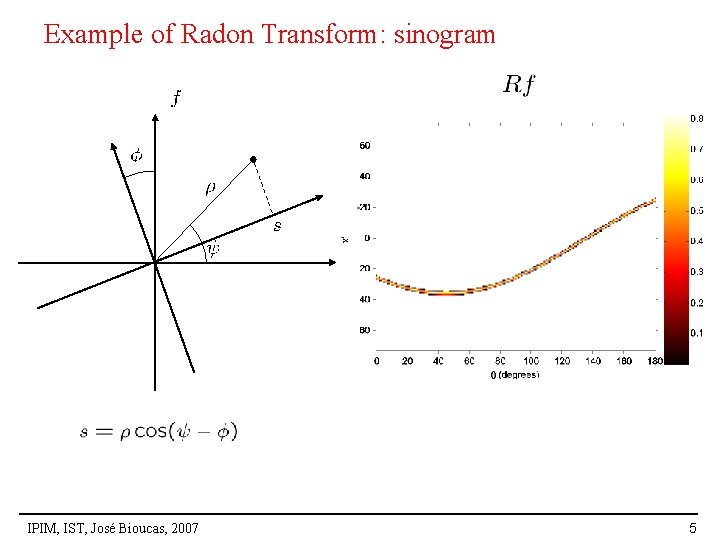
Example of Radon Transform: sinogram IPIM, IST, José Bioucas, 2007 5

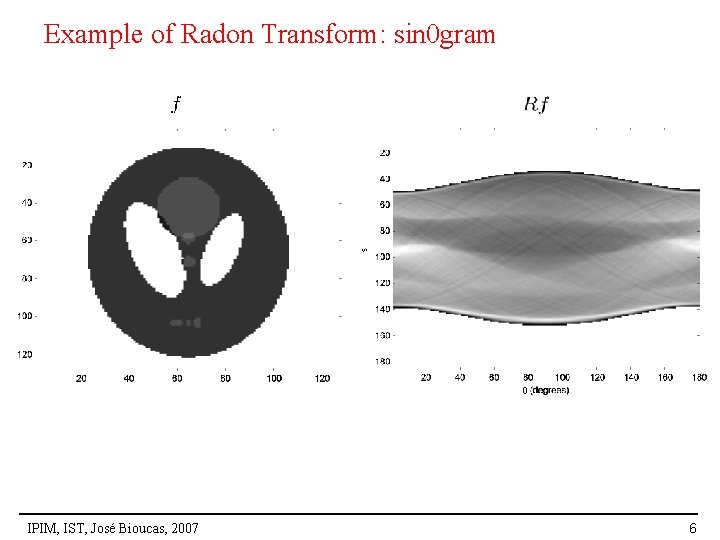
Example of Radon Transform: sin 0 gram IPIM, IST, José Bioucas, 2007 6

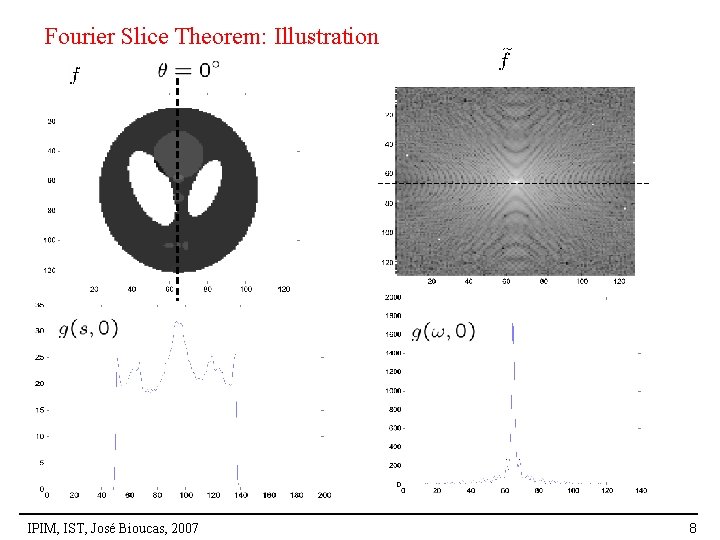
Fourier Slice Theorem IPIM, IST, José Bioucas, 2007 7

Fourier Slice Theorem: Illustration IPIM, IST, José Bioucas, 2007 8

Fourier Slice Theorem: Consequences 1 - The solution of the inverse problem is unique , when exists, 2 - The knowledge of the Radom transform of knowledge of the Fourier transform of implies the is spacelimited can be computed from samples taken apart IPIM, IST, José Bioucas, 2007 9

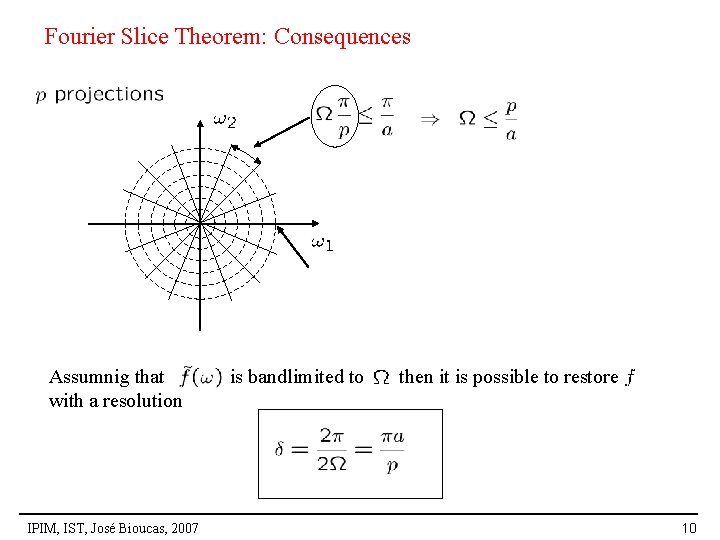
Fourier Slice Theorem: Consequences Assumnig that with a resolution IPIM, IST, José Bioucas, 2007 is bandlimited to then it is possible to restore 10

Backprojection Operator is the sum of all line integrals that crosses the point o IPIM, IST, José Bioucas, 2007 11

Backprojection Operator is the adjoint operator of when the usual inner product is considered for both the data functions and the objects IPIM, IST, José Bioucas, 2007 12

Backprojection Operator IPIM, IST, José Bioucas, 2007 13

Filtered Backprojection Algorithm periodic function of IPIM, IST, José Bioucas, 2007 14

Filtered Backprojection Algorithm From the Fourier slice theorem Defining the filtered backprojections as Then IPIM, IST, José Bioucas, 2007 15

IPIM, IST, José Bioucas, 2007 16

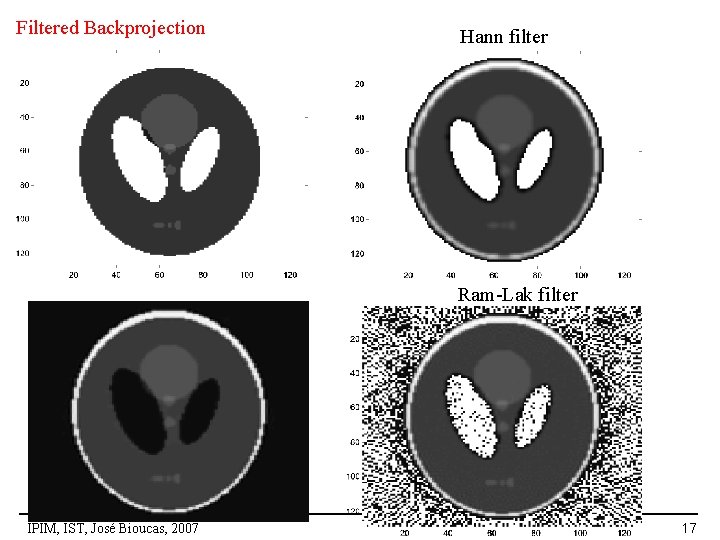
Filtered Backprojection Hann filter Ram-Lak filter IPIM, IST, José Bioucas, 2007 17

IPIM, IST, José Bioucas, 2007 18