XRANK Ranked Keyword Search over XML Documents Lin

XRANK: Ranked Keyword Search over XML Documents Lin Guo Feng Shao Chavdar Botev Jayavel Shanmugasundaram Presentation by: Meghana Kshirsagar Nitin Gupta Indian Institute of Technology, Bombay

Outline Motivation ● Problem Definition, Query Semantics ● Ranking Function ● A New Datastructure – Dewey Inverted List (DIL) ● Algorithms ● Performance Evaluation ●

Motivation

Motivation - I ● ● Why do we need search over XML data? Why not use search techniques used on WWW (keyword search on HTML)?

Motivation - II Keyword Search: XML Vs HTML ● ● HTML XML structural Links: document-to-document Tags: Format specifiers ● ● ranking ● ● ● Result: Document Page-level ranking Proximity: ● width: distance between words Links: IDREFs and Xlinks Tags: Content specifiers ● ● ● Result: XML element (a tree) Element-level ranking Proximity: ● width ● height

Problem Definition, Query Semantics, and Ranking

Problem Definition ● Input: Set of keywords ● Output: Ranked XML elements What is a result? How to rank results ?

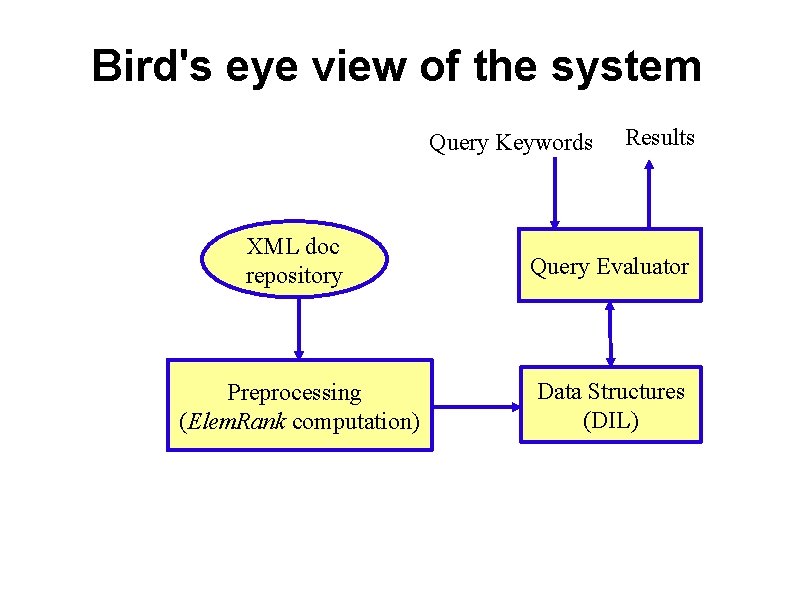
Bird's eye view of the system Query Keywords Results XML doc repository Query Evaluator Preprocessing (Elem. Rank computation) Data Structures (DIL)

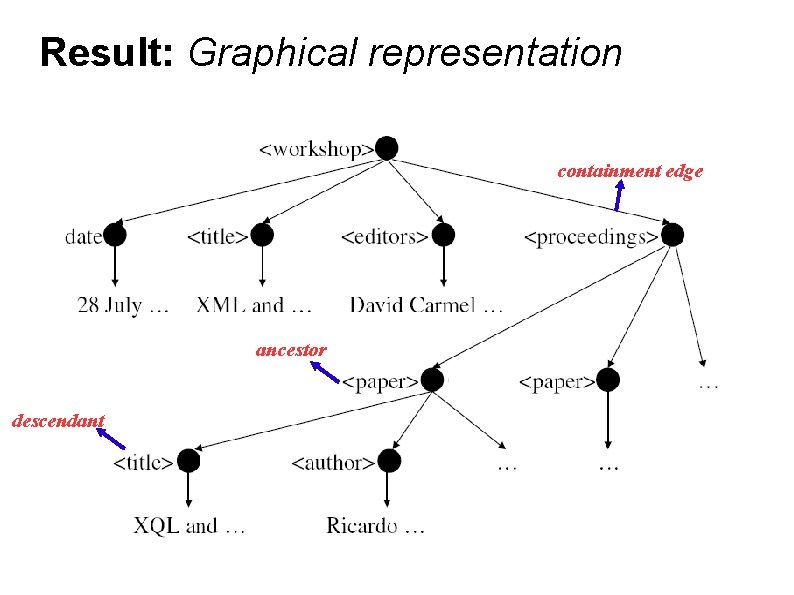
What is a result? ● ● A minimal Steiner tree of XML elements Result-set is a set of XML elements that ● includes a subset of elements containing all query-keywords at least once, after excluding the occurrences of keywords in contained results (if any).

result 1 result 2

Result: Graphical representation containment edge ancestor descendant

Ranking: Which results to return first? Properties: The Ranking function should ● reflect Result Specificity ● consider Keyword-Proximity ● be Hyperlink Aware Ranking function: f (height, width, link-structure)

Less specific result More specific result

Ranking Function For a single XML element (node): t-1 r (v 1, ki) = Elem. Rank ( vt ). decay v 1 v ki t

Ranking Function Combining ranks in case of multiple occurrences: Overall Rank:

Semantics of the ranking function Link structure t-1 r (v 1, ki) = Elem. Rank ( vt ). decay Specificity (height) Proximity

Elem. Rank Computation – adopt Page. Rank? ? ● Page. Rank ● Short-comings: Fails to capture: ✗ bidirectional transfer of “Elem. Ranks” ✗ discrimination between edge-types (containment and hyperlink) ✗ doesn't aggregate “Elem. Ranks” for reverse containment relationships

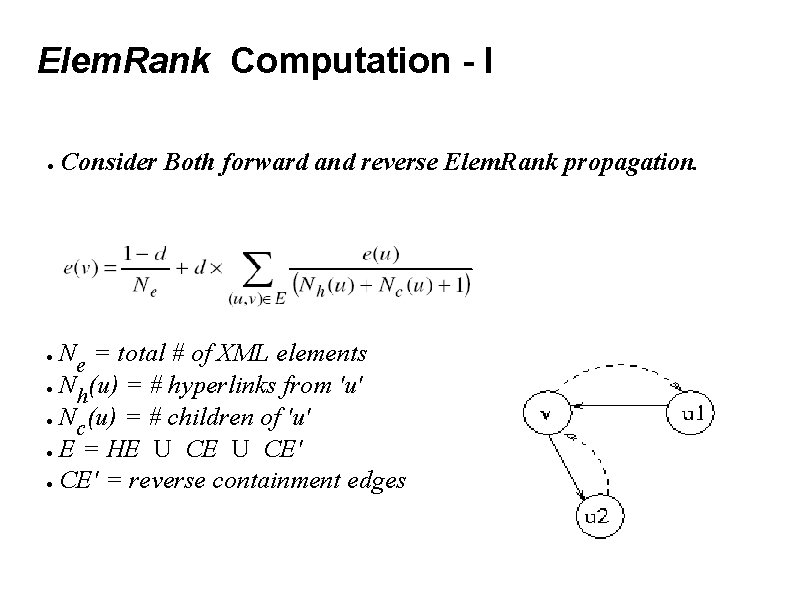
Elem. Rank Computation - I ● Consider Both forward and reverse Elem. Rank propagation. Ne = total # of XML elements ● N (u) = # hyperlinks from 'u' h ● N (u) = # children of 'u' c ● E = HE U CE' ● CE' = reverse containment edges ●

Elem. Rank Computation - II ● Seperate containment and hyperlink edges CE = containment edges ● HE = hyperlink edges ● Elem. Rank (sub elements) ● α 1 / ( # sibling sub-elements )

Elem. Rank Computation - III Sum over the reverse-containment edges, instead of distributing the weight ● Nd(u) = total # XML documents ● N de(v) = # elements in the XML doc containing v ● Elem. Rank (parent) α Sum (Elem. Rank(sub-elements)) ●

Datastructures and Algorithms

Naïve Algorithm Approach: ● ● XML element ~ doc Use “keyword search on WWW” Limitations: ● ● ● Space overhead (in inverted indices) Failure to model Hierarchical relationships (ancestor~decendent). Inaccurate Ranking Need a new datastructure which can model hierarchical relationships !! Answer: Dewey Inverted Lists

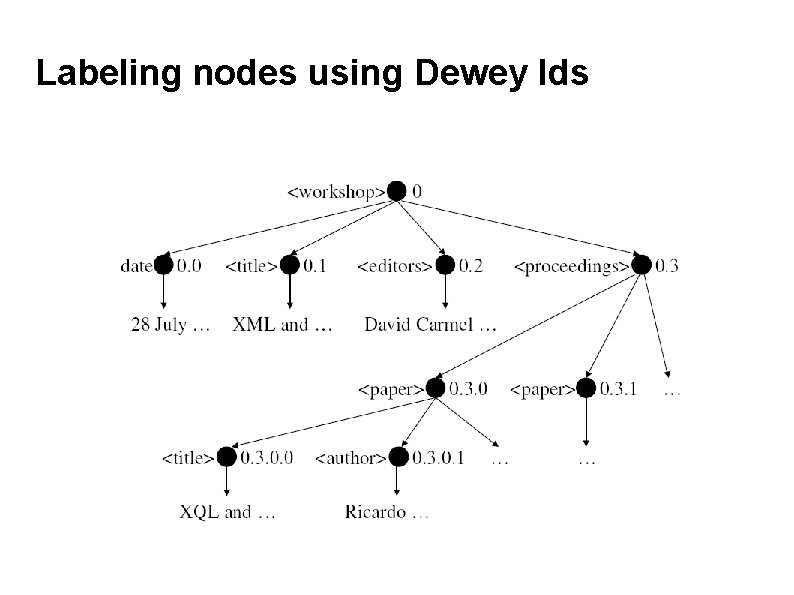
Labeling nodes using Dewey Ids

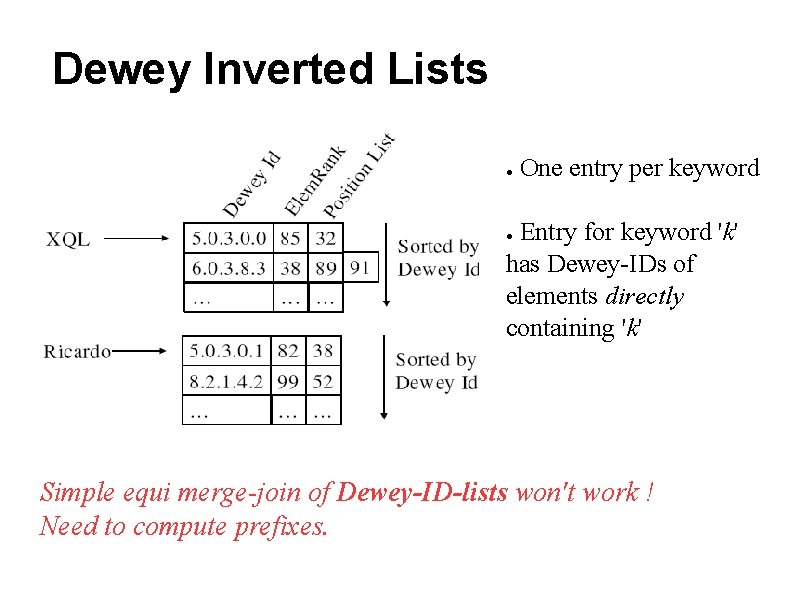
Dewey Inverted Lists ● One entry per keyword Entry for keyword 'k' has Dewey-IDs of elements directly containing 'k' ● Simple equi merge-join of Dewey-ID-lists won't work ! Need to compute prefixes.

System Architecture

DIL : Query Processing ● ● ● Simple equality merge-join will not work Need to find LCP (longest common prefix) over all elements with query keyword-match. Single pass over the inverted lists suffices! Compute LCP while merging the ILs of individual keywords. ILs are sorted on Dewey-IDs

Datastructures ● Array of all inverted lists : inverted. List[] ● ● inverted. List[i] for keyword 'i' each inverted. List[i] is sorted on Dewey-ID Heap to maintain top-m results : result. Heap Stack to store current Dewey-ID, ranks, position List, longest common prefixes : dewey. Stack

Algorithm on DILs - Abstract While all inverted-lists are not processed ● Read the next entry from DIL having smallest Dewey-ID ● call this 'current. Entry' Find the longest common prefix (lcp) between stack components and entry read from DIL ● ● lcp (dewey. Stack , current. Entry) Pop non-matching entries from Dewey-stack; Add result to heap if appropriate ● ● ● Push non-matching part of 'current. Entry' to 'dewey. Stack' ● ● check if current top-of-stack contains all keywords ● if yes, compute Overall. Rank, put this result onto heap ● else ● non-matching entries are popped one component at a time and update (rank, pos. List) on each pop non-matching components of 'current. Entry. dewey. ID' are pushed onto stack Update components of top entry of dewey. Stack

Example Query: “XQL Ricardo”

Algorithm Trace – Step 1 Rank[i] = Rank due to keyword 'i' Pos. List[i] = List of occurrences of keyword 'i' Smallest ID: 5. 0. 3. 0. 0 DIL: inverted. List[] Dewey. Stack push all components and find rank, pos. L

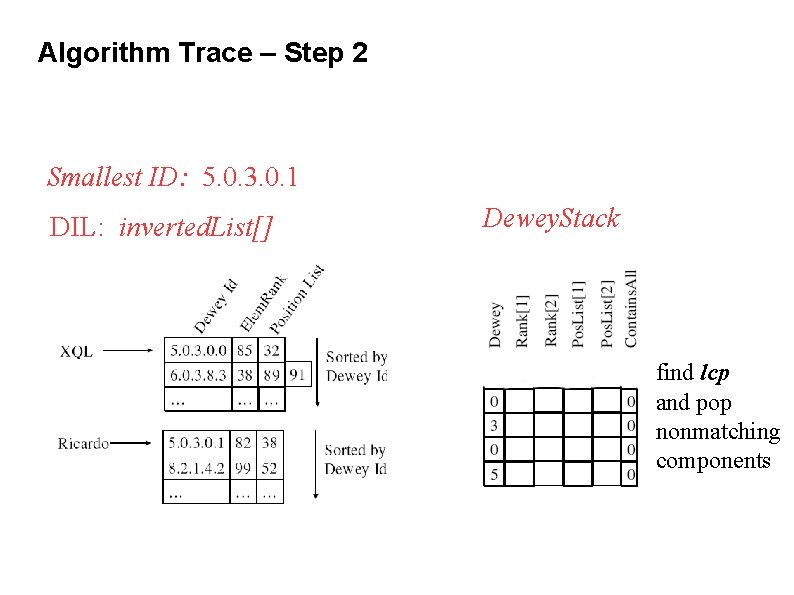
Algorithm Trace – Step 2 Smallest ID: 5. 0. 3. 0. 1 DIL: inverted. List[] Dewey. Stack find lcp and pop nonmatching components

Algorithm Trace – Step 3 Smallest ID: 5. 0. 3. 0. 1 DIL: inverted. List[] Dewey. Stack updated rank, pos. L

Algorithm Trace – Step 4 Smallest ID: 5. 0. 3. 0. 1 DIL: inverted. List[] Dewey. Stack push non-matching components

Algorithm Trace – Step 5 Smallest ID: 6. 0. 3. 8. 3 DIL: inverted. List[] Dewey. Stack find lcp, update, finally pop all components

Problems with DIL ● ● Scans the entire inverted-list for all keywords before a result is output Very inefficient for top-k computation

Other Techniques - RDIL ● Ranked Dewey Inverted List: ● For efficient top-k result computation ● IL is ordered by Elem. Rank ● Each IL has a B+ tree index on the Dewey. IDs ● Algorithm with RDIL uses a threshold

Algorithm using RDIL (Abstract) ● Choose the next entry from one of the inverted. List[] in a Round. Robin fashion. ● ● ● Find the longest common prefix that contains all query-keywords ● ● ● say chosen IL = inverted. List[i] d = top-ranked Dewey-ID from inverted. List[i] Probe the B+ tree index of all other keyword ILs, for the longest common prefix Claim: ● d 2 = smallest Dewey-ID in inverted. List[j] of query-keyword 'j' ● d 3 = immediate predecessor of d 2 ● lcp = max_prefix (lcp ( d, d 2) , lcp ( d, d 3)) Check if 'lcp' is a complete result Recompute 'threshold' = sum (Elem. Rank of last processed element in each query keyword IL) If (rank of top-k results on heap) >= threshold) return;

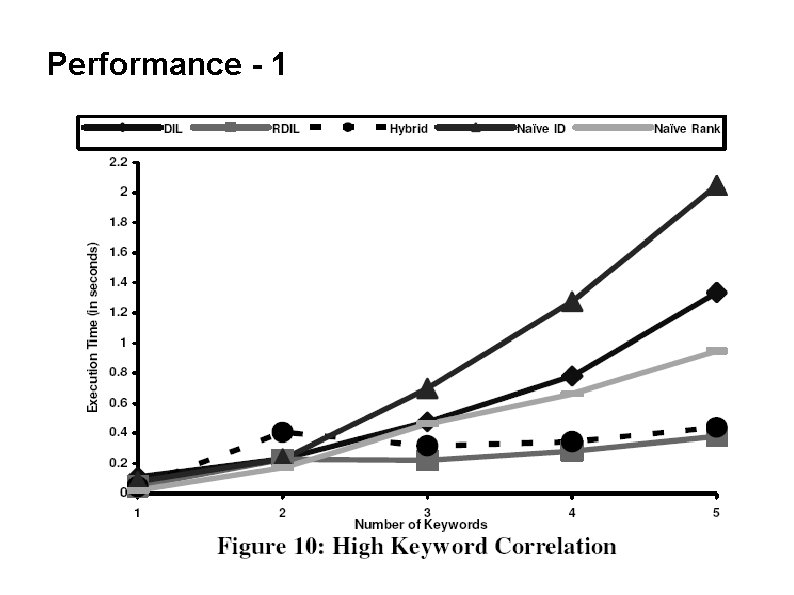
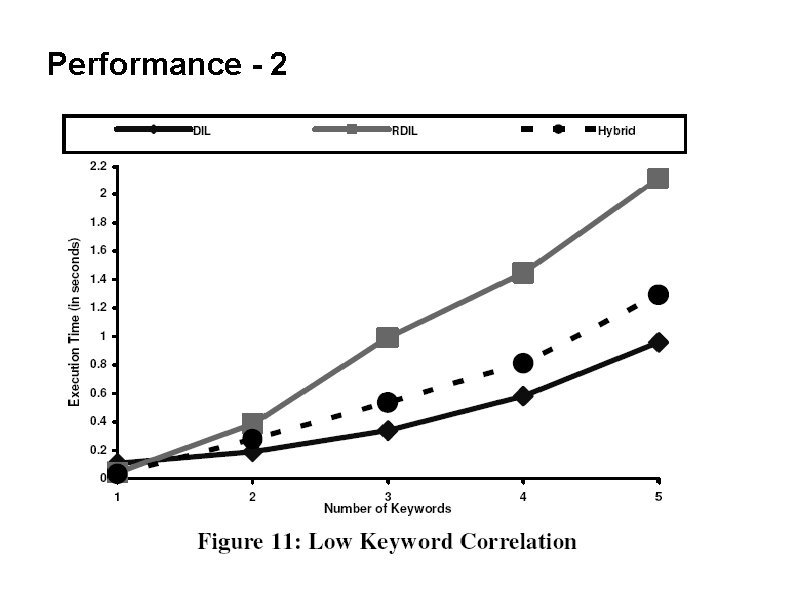
Performance of RDIL ● ● ● Works well for queries with highly correlated keywords BUT ! becomes equivalent (actually worse) to DIL for totally uncorrelated keywords Need an intermediate technique

HDIL ● Uses both DIL and RDIL ● Adaptive strategy: ● – Start with RDIL – Switch to DIL if performance is bad Performance? – – Estimated remaining time for RDIL = (m – r ) * t / r ● t = time spent so far ● r = no. of results above threshold so far ● m = desired no. of results Estimated remaining time for DIL ? ● No. of query-keywords is known ● Size of each IL is known

HDIL ● Datastructures? – Store full IL sorted on Dewey-ID – Store small fraction of IL sorted on Elem. Rank – Share the leaf level between IL and B+ tree (in RDIL) – Overhead : top levels of B+ tree

Updating the lists ● Updation is easy ● Insertion – very bad! – techniques from Tatarinov et al. – we've seen a better technique in this course : ) – Ord. Path

Evaluation ● ● Criteria: ● no. of query-keywords ● correlation between query-keywords ● desired no. of query results ● selectivity of keywords Setup: ● Datasets used: DBLP, Xmark ● d 1 = 0. 35, d 2 = 0. 25, d 3 = 0. 25 ● 2. 8 GHz Pentium IV + 1 GB RAM + 80 GB HDD

Performance - 1

Performance - 2

Critique New datastructure (DIL) defined to represent hierarchical relationships accurately and efficiently. ● Hyperlinks and IDREFs are considered only while computing Elem. Rank. Not used while returning results. ● Only containment edges (ancestor-descendant) are considered while computing result trees. ● Works only on trees, can't handle graphs. ●

The Sphere. Search Engine for Unified Banked Retrieval of Heterogenous XML and Web Documents Jens Graupmann Ralf Schenkel Gerhard Weikum Max-Plack-Institut fur Informatik Presentation by: Nitin Gupta Meghana Kshirsagar Indian Institute of Technology Bombay

Why another search engine ? ● ● ● To cope with diversity in the structures and annotations of the data Ranked retrieval paradigm for producing relevance ordered results lists rather than a mere boolean retrieval. Short comings of the current search engines – Concept aware – Context aware (or link-awareness) – Abstraction aware – Query Language

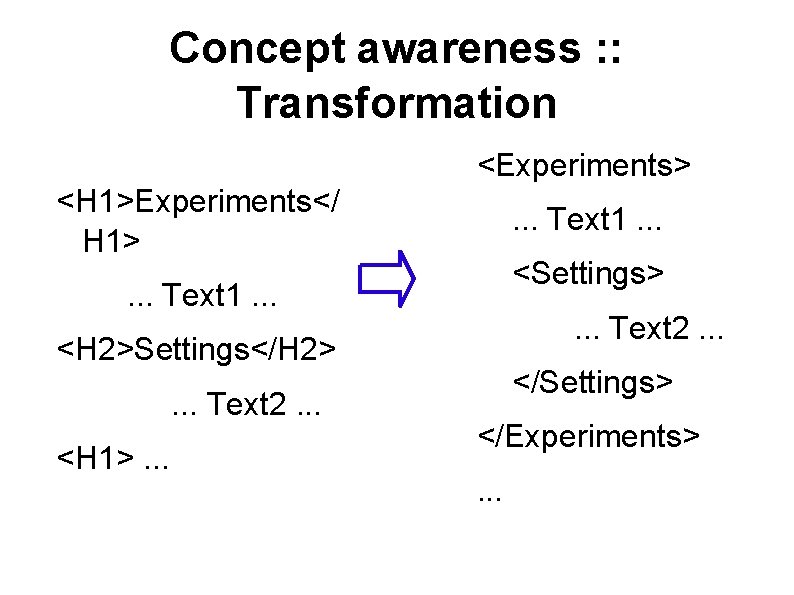
Concept awareness ● ● ● Example: researcher max planck yields many results about researchers who work at the institute “Max Plack” Society Better formulation would be researcher person=“max planck” Objective attained by – Transformation to XML – Data Annotation

Concept awareness : : Transformation <Experiments> <H 1>Experiments</ H 1> . . . Text 1. . . <Settings> . . . Text 1. . . Text 2. . . <H 2>Settings</H 2>. . . Text 2. . . <H 1>. . . </Settings> </Experiments>. . .

Abstraction Awareness ● ● ● Example: Synonyms, Ontologies Is connection to various encyclopedias/ Wiki's possible? Objective attained by using – Ontology Service: provides quantified ontological information to the system – Preprocessed information based on focused web crawls to estimate statistical correlations between the characteristic words of related concepts

Context Awareness ● ● Query may not be answered by web search engines as no single web page may be a match Unlike usual navigation axes in XML, context should go beyond trees. Consider graph structure spanned by Xlink/XPointer references and href hyperlinks Objective attained by – introduction of the concept of a SPHERE

Context Awareness : : Sphere ● What is a sphere? – Relevance of an element for a group of query conditions is not just determined by its own content, but also by the content of other neighboring elements, including linked documents, in an environment - called Sphere - of the element.

Query Language ● ● ● Query S = (Q, J) consists of – set Q = { G 1. . Gq } of query groups – set J = { J 1. . Jm } of join conditions Each Qi consists of – set of keyword conditions t 1. . tk – set of concept value conditions c 1 = v 1. . . cl = vl Each join has the form Qi. v = (or ~) Qj. w

Query Language ● Example: German professors who teach database courses – P(professor, location=~Germany) and have projects on XML – C(course, ~databases) – R(~project, ~XML) – A(gothic, church) – B(romanic, church) – A. location = B. location Gothic and Romanic churches at the same location

Data Model ● ● ● Collection X = (D, L) of XML documents D together with a set L of (href, Xpointer, or Xlink) links between their elements Consider all attributes as elements: then element level graph GE(X) = (VE(X), EE(X)) has the union of all the elements of the document as nodes and undirected edges between them Each edge has nonnegative weight – ● 1 for parent-child; ‘λ’ for links A distance function δX(x, y) : computes weight of a shortest path in GE(X) between x and y

Spheres and Query Groups ● ● Node-score ns(n, t) is computed using Okapi BM 25 model Similarity condition ~K: Compute exp(K) for the keyword. The node score is defined as max xЄexp(K) sim(K, x) * ns(n, x) where sim(K, x) is the ontological similarity ● Concept value: – – { ns(n, c=v) = 0 ns(n, v) if name(n) ≠ c otherwise ● Similarity concept value: ~c = v: sim(name(n), c) * ns(n, v) ● This is insufficient – in the presence of linked documents – when content is spread over several elements

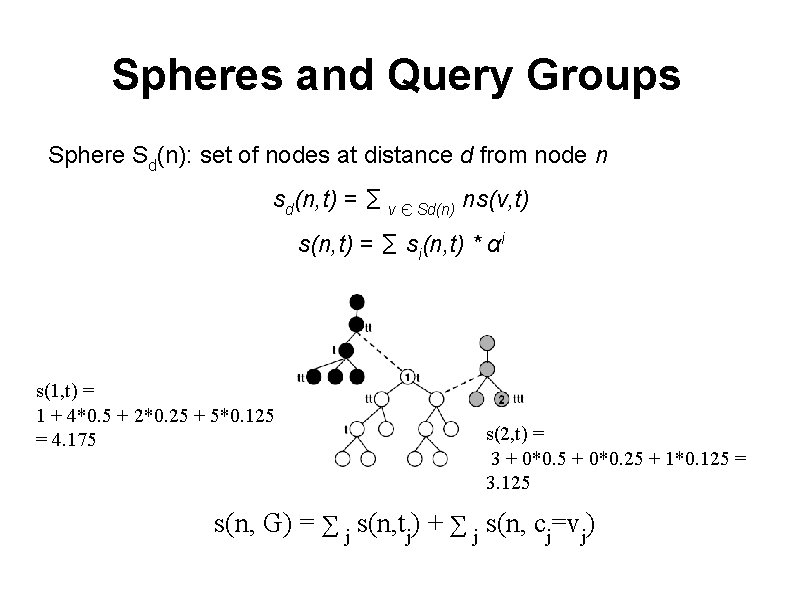
Spheres and Query Groups Sphere Sd(n): set of nodes at distance d from node n sd(n, t) = ∑ v Є Sd(n) ns(v, t) s(n, t) = ∑ si(n, t) * αi s(1, t) = 1 + 4*0. 5 + 2*0. 25 + 5*0. 125 = 4. 175 s(2, t) = 3 + 0*0. 5 + 0*0. 25 + 1*0. 125 = 3. 125 s(n, G) = ∑ j s(n, tj) + ∑ j s(n, cj=vj)

Spheres and Query Groups : : Ranking Create a connection graph G(N) = (V(N), E(N)) Weight of an edge between x, y: 0 if x and y are not connected 1/ δx(x, y)+1 otherwise Compactness C(N) of a potential answer N is then the sum of the total edge weights of a maximal spanning tree for G(N), and the score is given by: s(N, S) = β C(N) + (1 - β) ∑i s(ni, Gi)

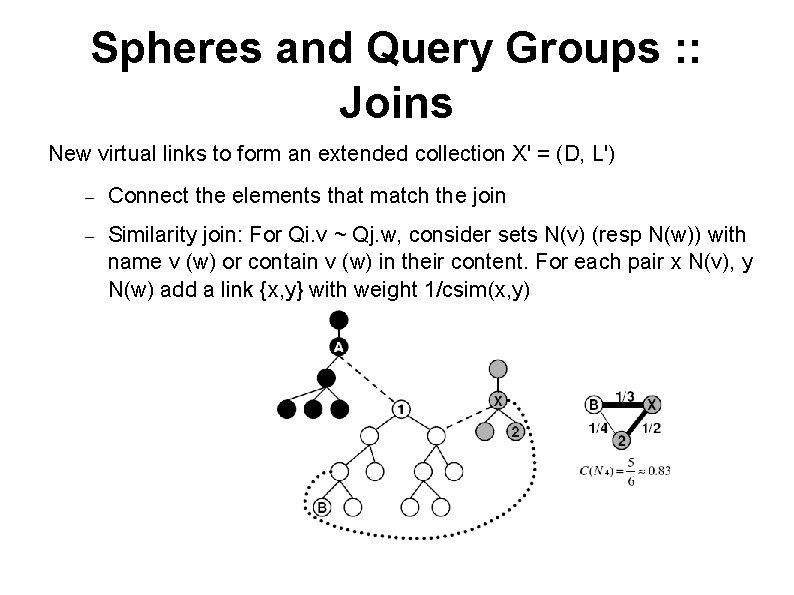
Spheres and Query Groups : : Joins New virtual links to form an extended collection X' = (D, L') – Connect the elements that match the join – Similarity join: For Qi. v ~ Qj. w, consider sets N(v) (resp N(w)) with name v (w) or contain v (w) in their content. For each pair x N(v), y N(w) add a link {x, y} with weight 1/csim(x, y)

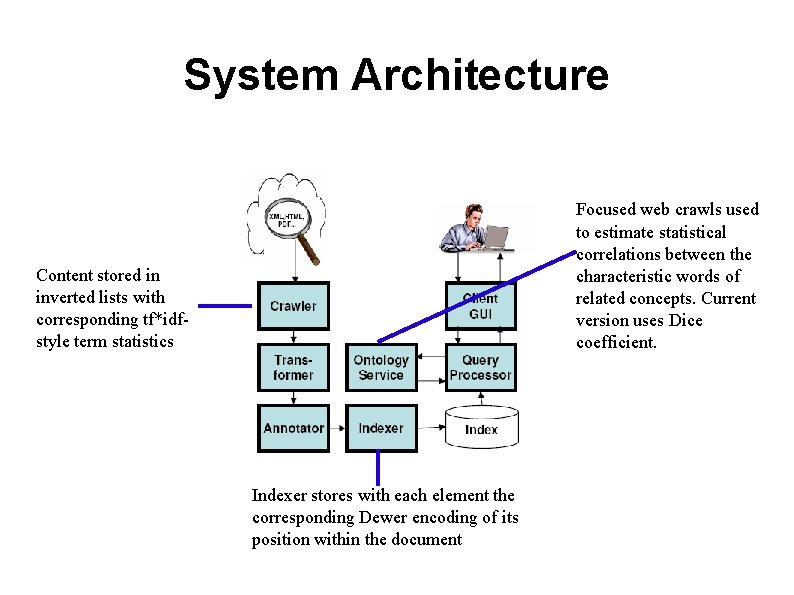
System Architecture Focused web crawls used to estimate statistical correlations between the characteristic words of related concepts. Current version uses Dice coefficient. Content stored in inverted lists with corresponding tf*idfstyle term statistics Indexer stores with each element the corresponding Dewer encoding of its position within the document

Query Processor 1. First compute a result list for each query group 2. Add virtual links for join conditions 3. Compute the compactness of a subset of all potential answers of the query in order to return the top-k results 1. Compute a list of results for each of query keywords and concept-value conditions. 2. Candidate nodes: Nodes that are at distance at most D from any node that occurs in at least one of the lists. Sphere score is computed only for these nodes since only these can have a non-zero score! 3. For eachl candidate node N, look up the node scores of nodes in the sphere of N, and adding these scores with a proper damping factor.

Query Processor ● ● ● Virtual links: Processor considers only a limited set of possible end points for efficient computation Nodes in the spheres upto distance D around nodes with nonzero sphere score for any query group – Why? Any other node will have distance atleast D+1 to any results node and thus contributes at most 1/ (D+1)+1 to the compactness, which is negligible – This set of candidate nodes can be computed on the fly Set further reduced by testing join attributes, for example A. x = B. y results in two sets of potential end points.

Query Processor ● Generating answers – Naïve method: generate all possible potential answers from the answers to query groups, compute connection graphs and compactness, and finally their score – For top-k answers, use Fagin's Threshold Algorithm with sorted lists only ● ● Input: Sorted list of node scores and pairwise node scores (edges) Output: k potential answers with the best scores

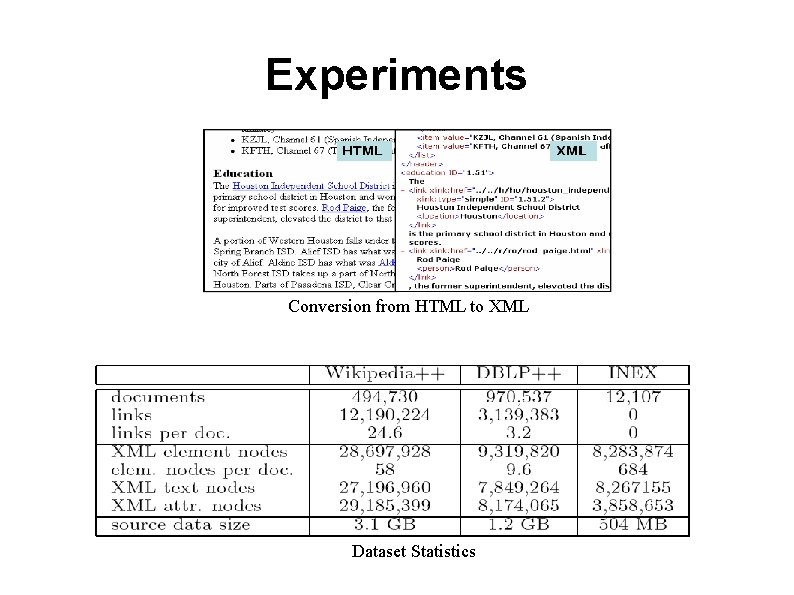
Experiments ● ● Sun V 40 z, 16 GB RAM, Windows 2003 Server, Tomcat 4. 0. 6 environment, Oracle 10 g database Benchmarks: XMach, Xmark, INEX, TREC Does not consider Designed for XQuery-style exact match Semantically poor tags XML at all Wikipedia Collection from the Wikipedia project: HTML Collection transformed into XML and annotated Wikipedia++ Collection: Extension of Wikipedia with IMDB data, with generated XML files for each movie and actor DBLP++ Collection: Based on the DBLP project which indexes more than 480, 000 publications INEX: Set of 12, 107 XML documents, a set of queries with and without structural constraints

Experiments Conversion from HTML to XML Dataset Statistics

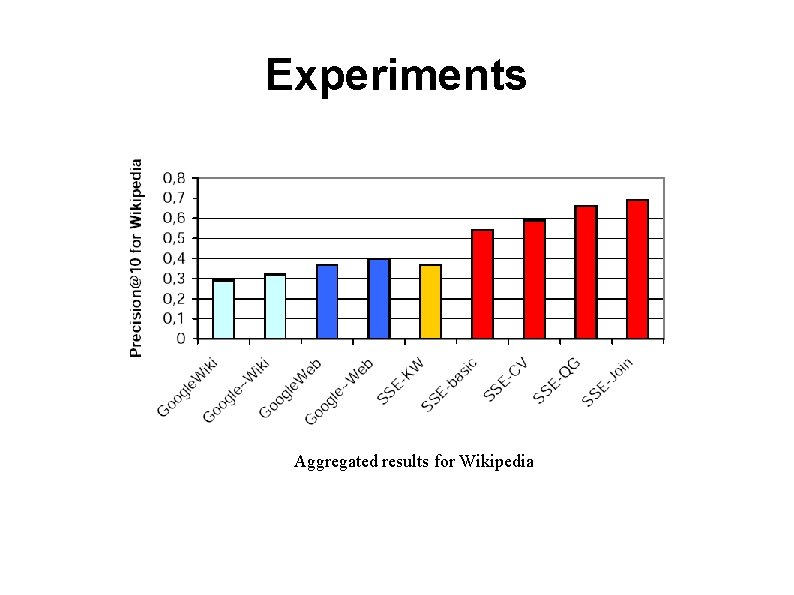
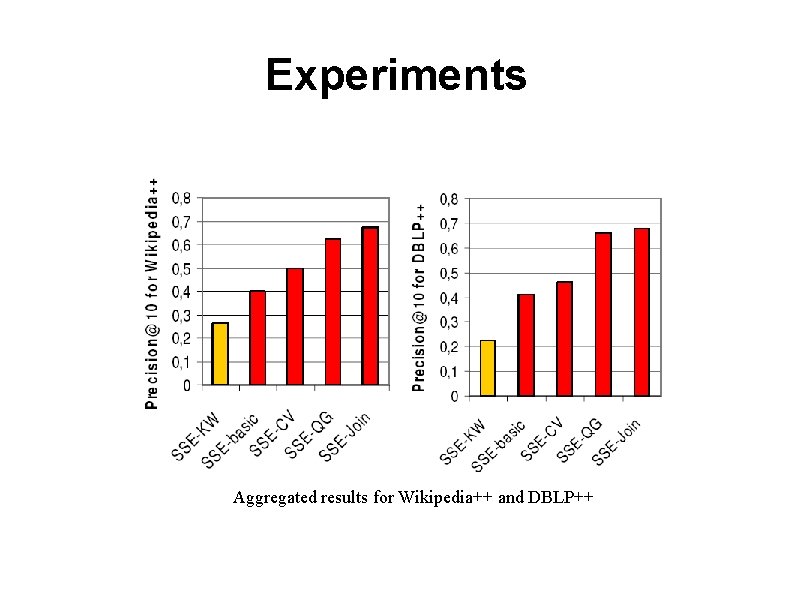
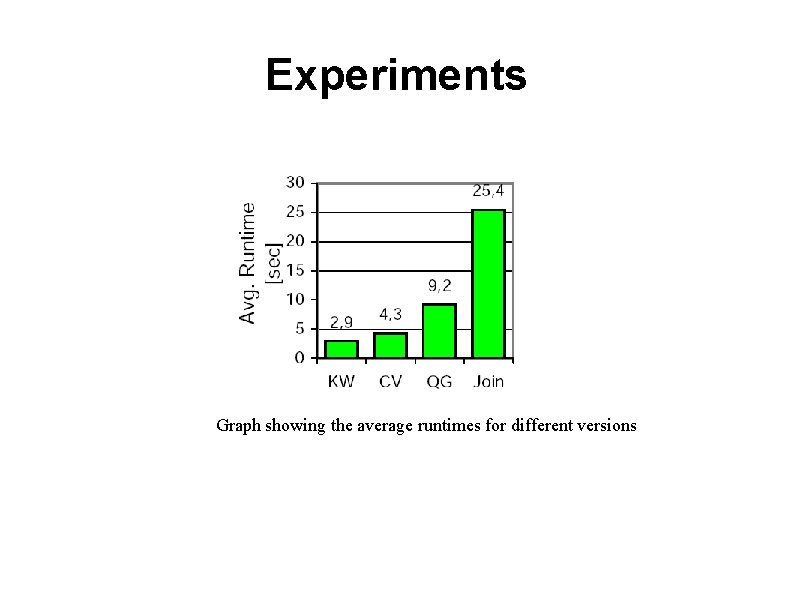
Experiments ● SSE-basic: basic version limited to keyword conditions using spherebased scoring ● SSE-CV: basic version plus concept-value conditions ● SSE-QC: CV version plus query groups (full contest awareness) ● SSE-Join: full version will all features ● SSE-KW: very restricted version with simple keyword search ● Google. Wiki: Google search restricted to Wikipedia. org ● Google~Wiki: Google on wikipedia. org with Google's ~ operator for query expansion ● Google. Web: Google search on the entire web ● Google~Web: Google search on the entire web with query expansion

Experiments Aggregated results for Wikipedia

Experiments Aggregated results for Wikipedia++ and DBLP++

Experiments Graph showing the average runtimes for different versions

Thank you