XPPAUT Differential Equations Tool B Ermentrout J Rinzel

XPPAUT Differential Equations Tool B. Ermentrout & J. Rinzel

Preliminary Remarks • Nonlinear ODEs do not usually have closed form solutions • Numerical solutions are needed • Qualitative analysis: phase plane analysis, bifurcation analysis, stability of steady states • XPPAUT can do all that for us! FOR FREE!

Focus of this presentation: We will use XPPAUT for solving : -Fitz. Hugh-Nagumo model of excitable membrane -Population growth model with time delay -Model of intracellular Calcium regulation
![Fitzhugh-Nagumo Neuron[2 & 3. p 161 -163 & 4. p 422 -431] • Simple Fitzhugh-Nagumo Neuron[2 & 3. p 161 -163 & 4. p 422 -431] • Simple](http://slidetodoc.com/presentation_image_h2/82b7474ed99d1be3c4f1c9cba0c0bd39/image-4.jpg)
Fitzhugh-Nagumo Neuron[2 & 3. p 161 -163 & 4. p 422 -431] • Simple model of an excitable membrane:

Iapplied=0
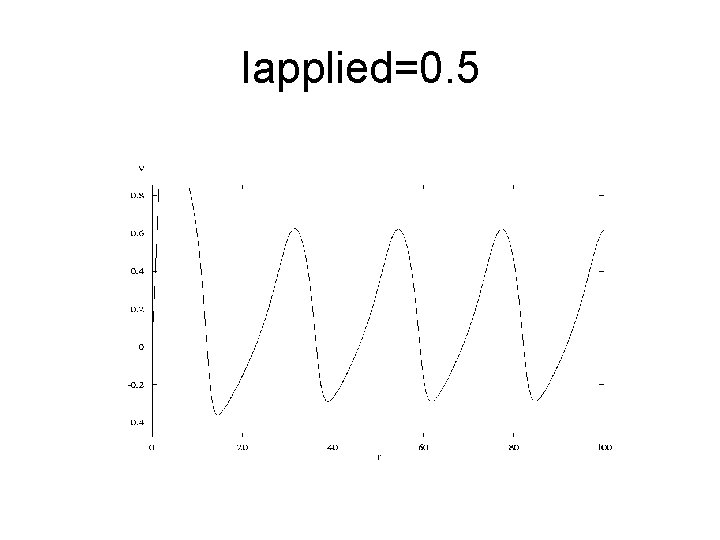
Iapplied=0. 5
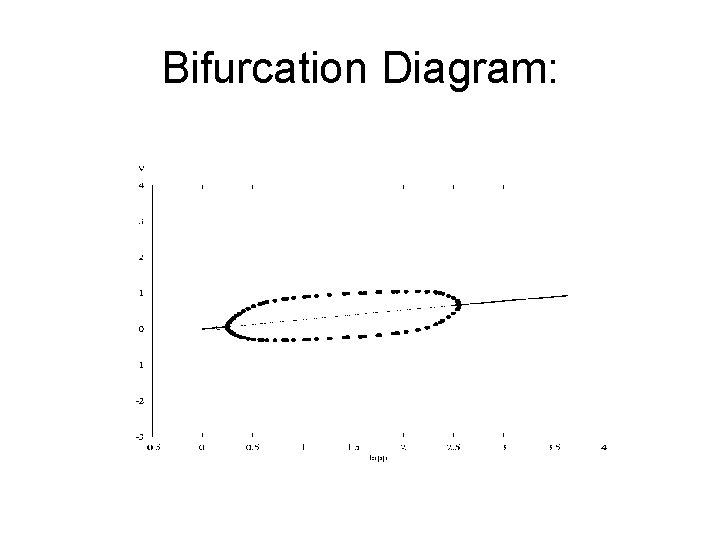
Bifurcation Diagram:
![Population Growth Model[3. p 2 -9] • Simple model of growth: • Population Growth Model[3. p 2 -9] • Simple model of growth: •](http://slidetodoc.com/presentation_image_h2/82b7474ed99d1be3c4f1c9cba0c0bd39/image-8.jpg)
Population Growth Model[3. p 2 -9] • Simple model of growth: •

Solution:

Sample Curve:

Introduction of Time Delay • No closed-form solution available • Dynamic is more interesting
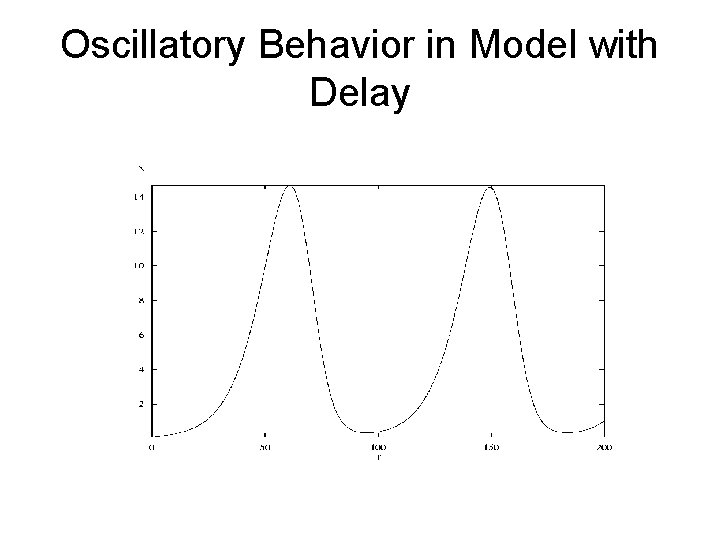
Oscillatory Behavior in Model with Delay

Calcium Regulation Proc. Natl. Acad. Sci. U. S. A. (1990) 78, 1461 -1465

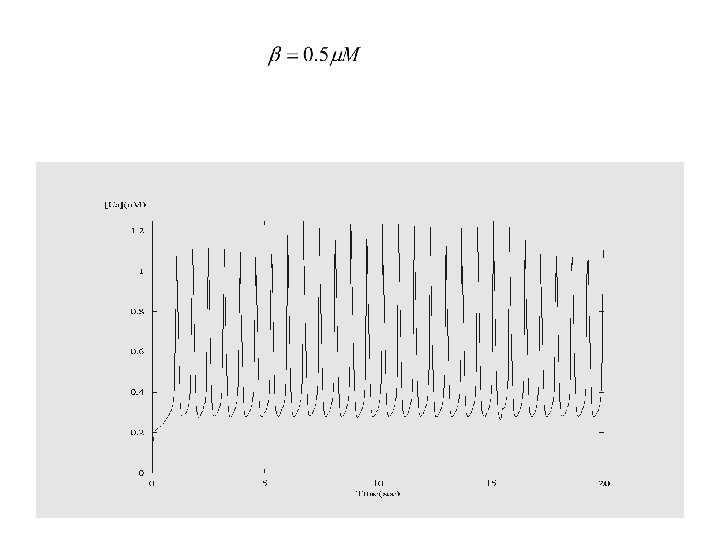
Role of IP 3( ) • Base parameter values are:
![[Ca] vs. Time(s) [Ca] vs. Time(s)](http://slidetodoc.com/presentation_image_h2/82b7474ed99d1be3c4f1c9cba0c0bd39/image-15.jpg)
[Ca] vs. Time(s)
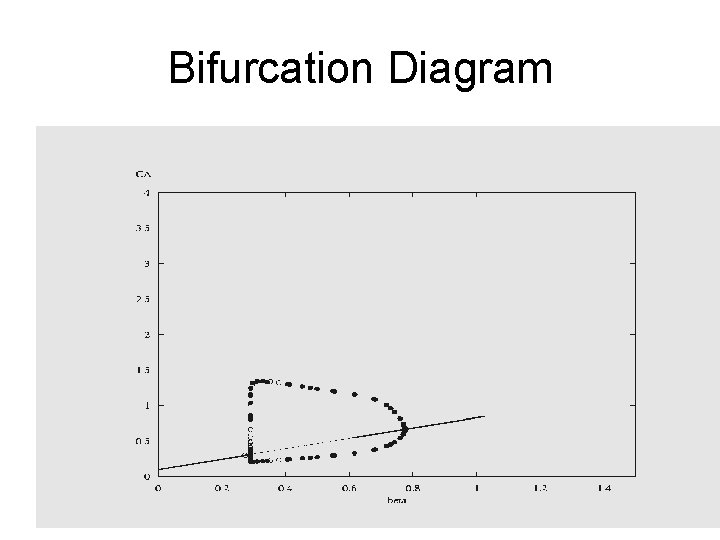
Bifurcation Diagram
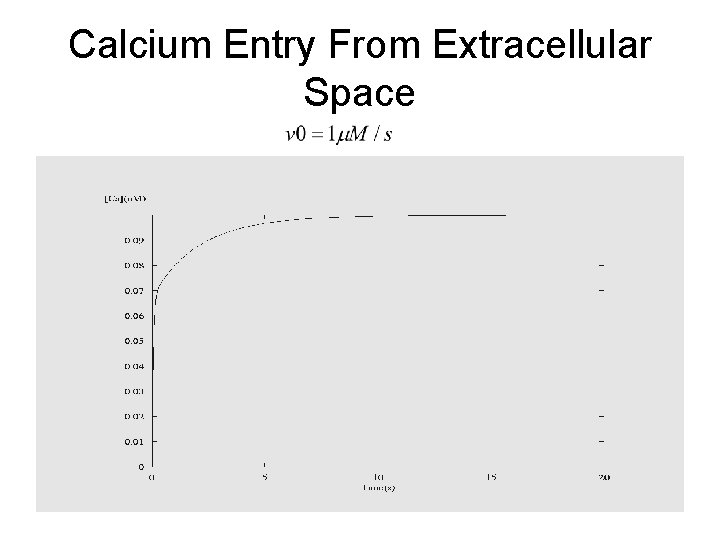
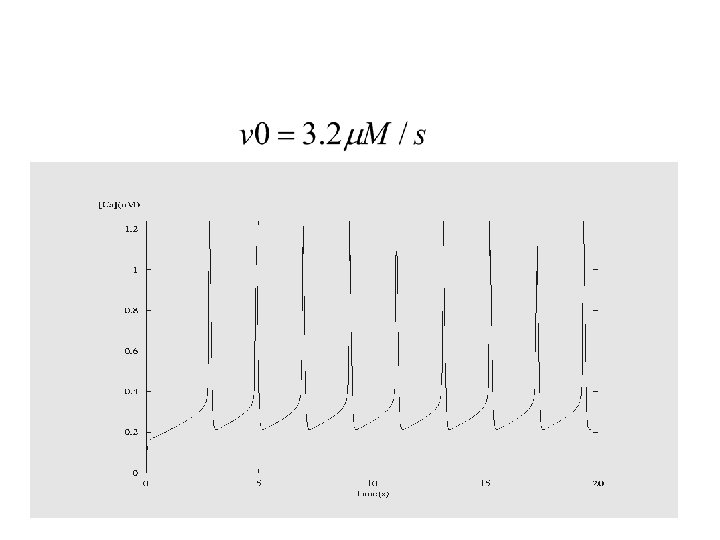
Calcium Entry From Extracellular Space
![[Ca] in ER [Ca] in ER](http://slidetodoc.com/presentation_image_h2/82b7474ed99d1be3c4f1c9cba0c0bd39/image-20.jpg)
[Ca] in ER
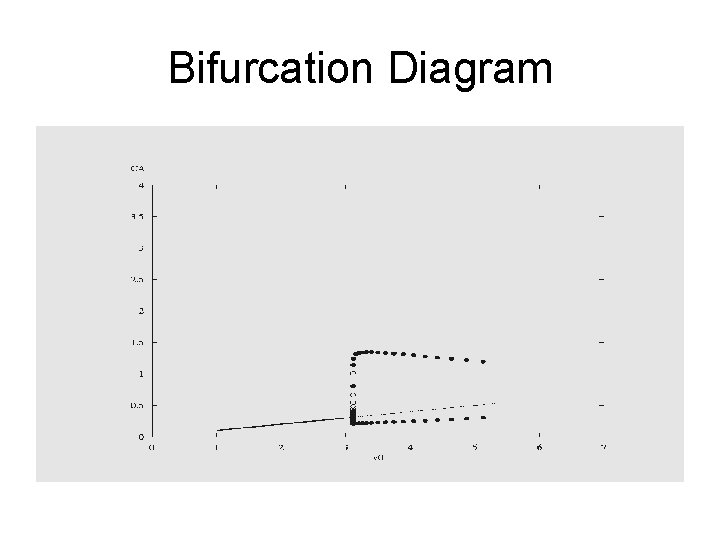
Bifurcation Diagram

Conclusion • XPPAUT is a powerful tool for: • Solving ordinary and delay differential equations • Understanding the solution through bifurcation analysis.
![References • [1] Goldbeter, A. , Dupont, G. , and Berridge, M. (1990). Proc. References • [1] Goldbeter, A. , Dupont, G. , and Berridge, M. (1990). Proc.](http://slidetodoc.com/presentation_image_h2/82b7474ed99d1be3c4f1c9cba0c0bd39/image-23.jpg)
References • [1] Goldbeter, A. , Dupont, G. , and Berridge, M. (1990). Proc. Natl. Acad. Sci. U. S. A. 87 1461 -1465. • [2] Fitz. Hugh, R. (1961). Biophys J. 1, 445 -466 • [3] Murray J. (1989). Mathematical Biology, 1 st edition, Springer-Verlag, New York. • [4] Fall, C, et al, (2002) Computational Cell Biology, 1 st edition, Springer-Verlag, New York • [5] Bard Ermentrout XPPAUT 5. 41 Differential equations tool(August, 2002) • www. math. pitt. edu/~bard/xpp. html
- Slides: 23