XIII Quark Confinement and Hadron Spectroscopy 4 Aug

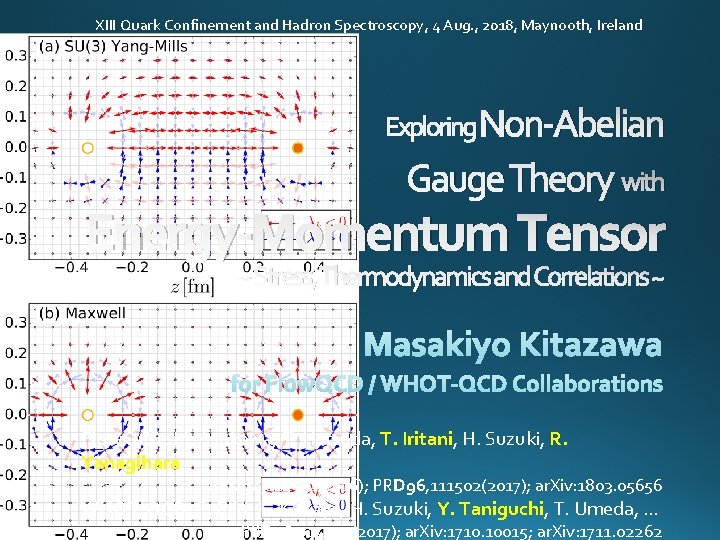
XIII Quark Confinement and Hadron Spectroscopy, 4 Aug. , 2018, Maynooth, Ireland Exploring Non-Abelian Gauge Theory with Energy-Momentum Tensor ~ Stress, Thermodynamics and Correlations ~ Flow. QCD: M. Asakawa, T. Hatsuda, T. Iritani, H. Suzuki, R. Yanagihara PRD 94, 114512(2016); PRD 96, 111502(2017); ar. Xiv: 1803. 05656 WHOT-QCD: S. Ejiri, K. Kanaya, H. Suzuki, Y. Taniguchi, T. Umeda, … PRD 96, 014509(2017); ar. Xiv: 1710. 10015; ar. Xiv: 1711. 02262

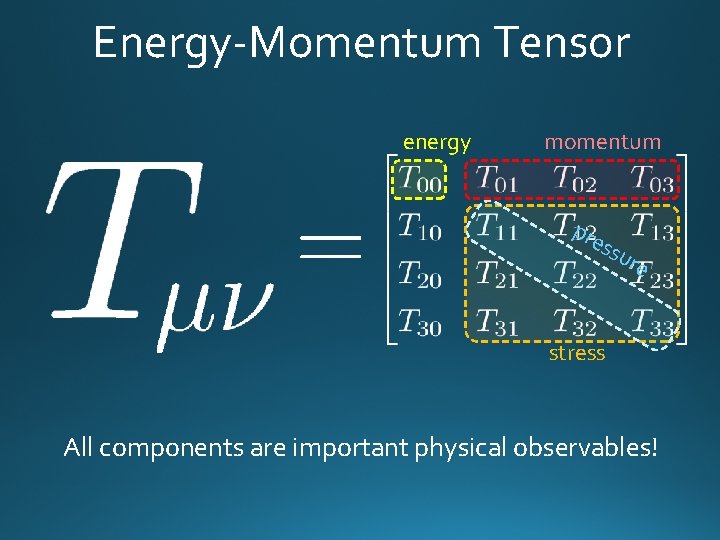
Energy-Momentum Tensor One of the most fundamental quantities in physics

Energy-Momentum Tensor energy momentum pre ssu r e stress All components are important physical observables!

: nontrivial observable on the lattice Definition of the operator is nontrivial ① because of the explicit breaking of Lorentz symmetry ex: Its measurement is extremely noisy ② due to high dimensionality and etc.

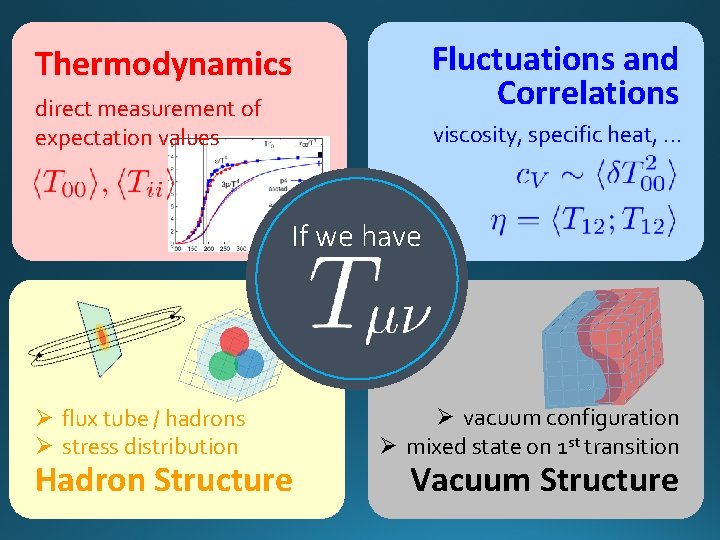
Fluctuations and Correlations Thermodynamics direct measurement of expectation values viscosity, specific heat, . . . If we have Ø flux tube / hadrons Ø stress distribution Hadron Structure Ø vacuum configuration Ø mixed state on 1 st transition Vacuum Structure

Constructing EMT on the lattice Thermodynamics EMT Correlation Function Stress distribution in qq system ー

Lattice EMT Operator Caracciolo+, 1990 p Fit to thermodynamics: Z 3, Z 1 p Shifted-boundary method: Z 6, Z 3 Giusti, Meyer, 2011; 2013; Giusti, Pepe, 2014~; Borsanyi+, 2018 Multi-level algorithm p effective in reducing statistical error of correlator Meyer, 2007; Borsanyi, 2018; Astrakhantsev+, 2018

Luscher 2010 Narayanan, Neuberger, 2006 Luscher, Weiss, 2011 t: “flow time” dim: [length 2] leading p diffusion equation in 4 -dim space p diffusion distance　 p “continuous” cooling/smearing p No UV divergence at t>0

Luscher 2010 Narayanan, Neuberger, 2006 Luscher, Weiss, 2011 t: “flow time” dim: [length 2] Applications leading scale setting / topological charge / running coupling noise reduction / defining operators / …

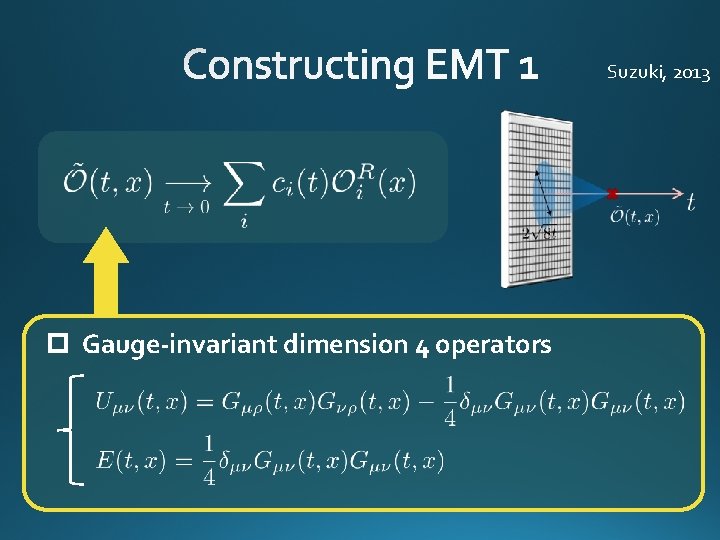
Luescher, Weisz, 2011 Suzuki, 2013 original 4 -dim theory an operator at t>0 t 0 limit remormalized operators of original theory

Suzuki, 2013 p Gauge-invariant dimension 4 operators

Suzuki, 2013 Suzuki coeffs. Remormalized EMT

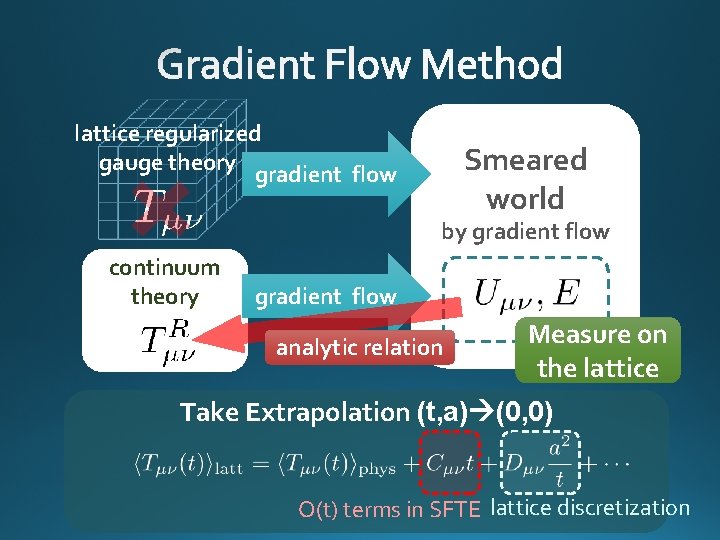
lattice regularized gauge theory gradient flow Smeared world by gradient flow continuum theory gradient flow analytic relation Measure on the lattice Take Extrapolation (t, a) (0, 0) O(t) terms in SFTE lattice discretization

Constructing EMT on the lattice Thermodynamics EMT Correlation Function Stress distribution in qq system ー

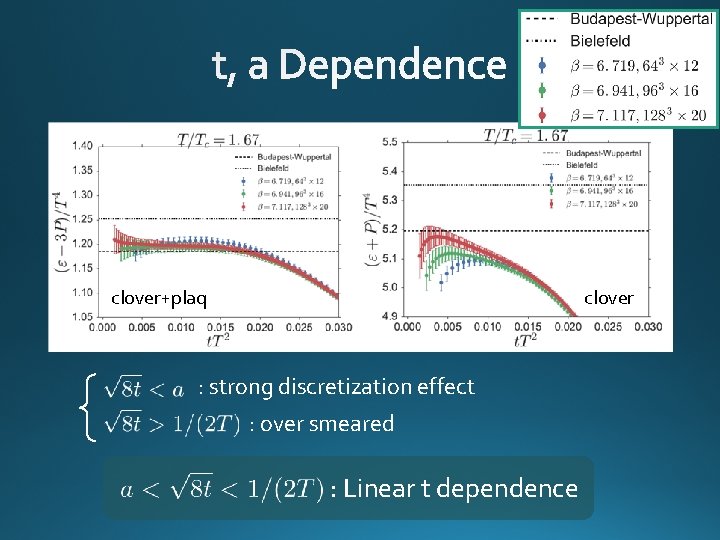
clover+plaq clover : strong discretization effect : over smeared : Linear t dependence

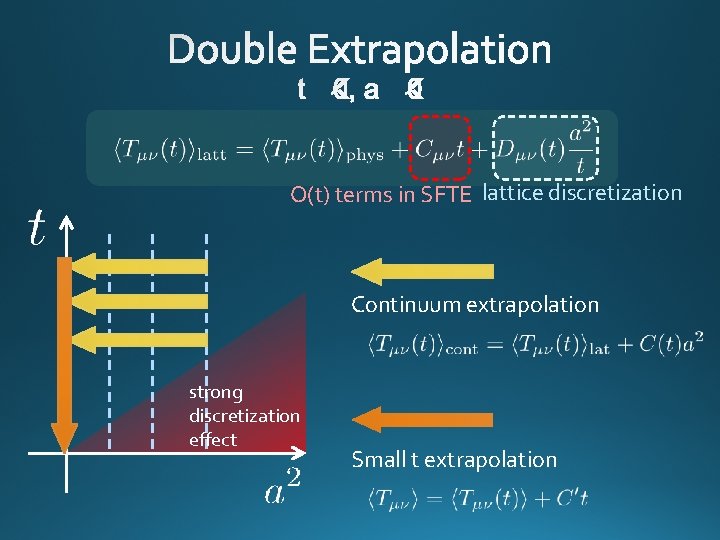
O(t) terms in SFTE lattice discretization Continuum extrapolation strong discretization effect Small t extrapolation

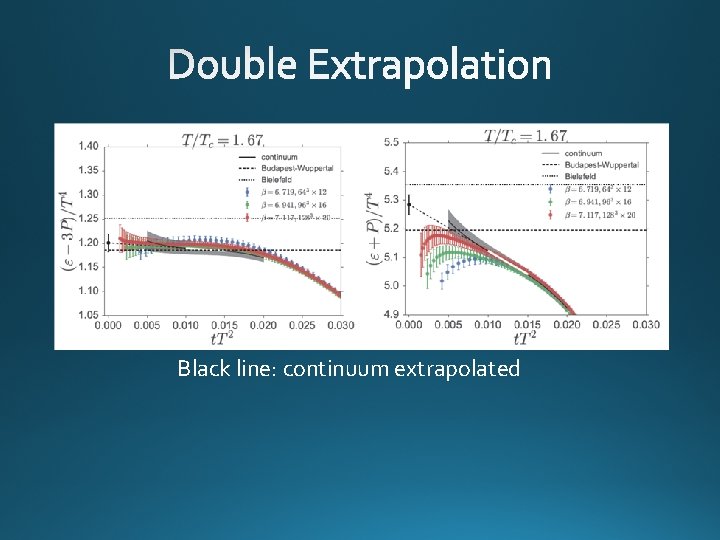
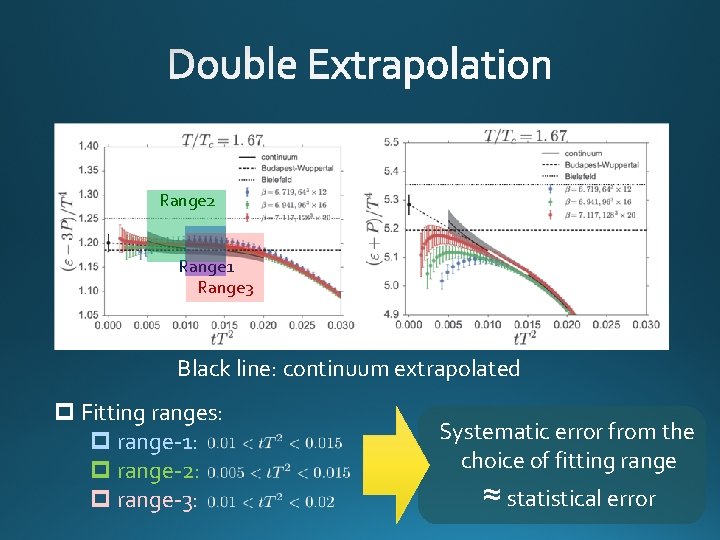
Black line: continuum extrapolated

Range 2 Range 1 Range 3 Black line: continuum extrapolated p Fitting ranges: p range-1: p range-2: p range-3: Systematic error from the choice of fitting range ≈ statistical error

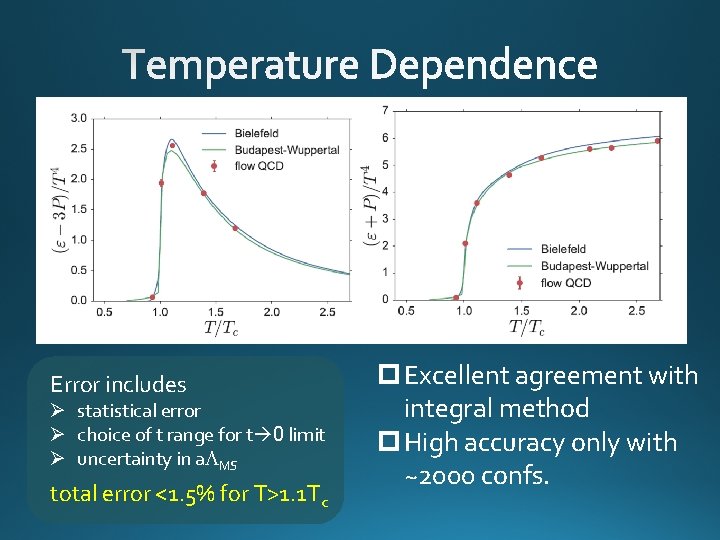
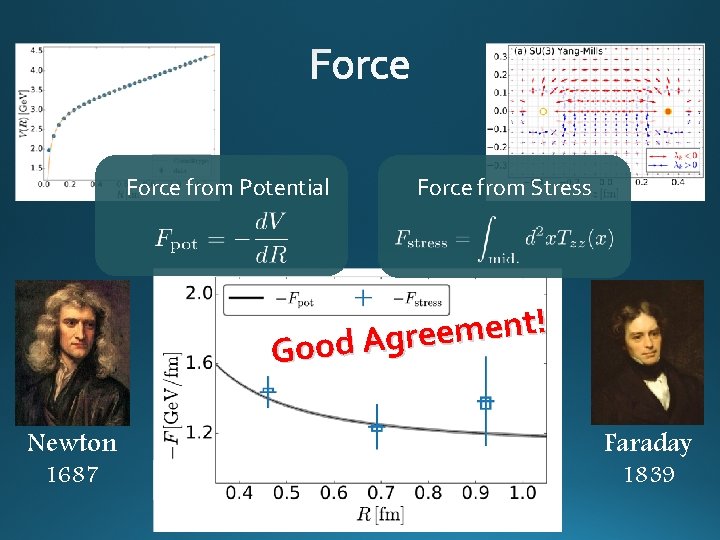
Error includes Ø statistical error Ø choice of t range for t 0 limit Ø uncertainty in a. LMS total error <1. 5% for T>1. 1 Tc p Excellent agreement with integral method p High accuracy only with ~2000 confs.

p Integral method p Most conventional / established p Use themodynamic relations Boyd+ 1995; Borsanyi, 2012 p Gradient-flow method p Take expectation values of EMT Flow. QCD, 2014, 2016 p Moving-frame method Giusti, Pepe, 2014~ p Non-equilibrium method p Use Jarzynski’s equality Caselle+, 2016; 2018 p Differential method Shirogane+(WHOT-QCD), 2016~

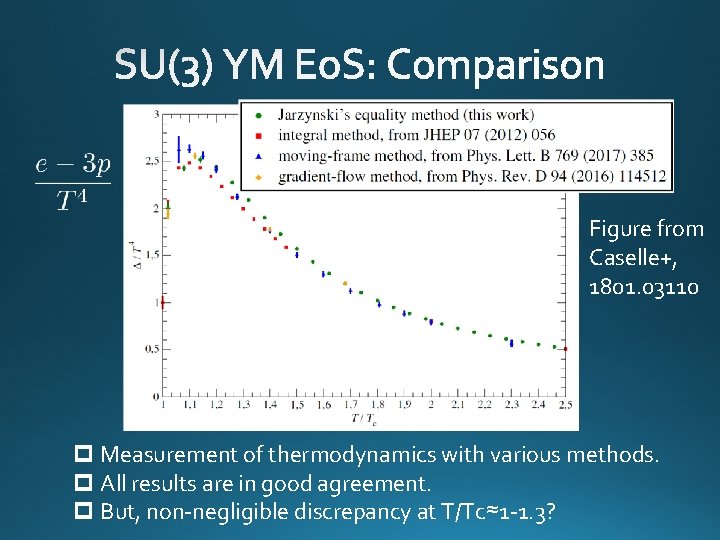
Figure from Caselle+, 1801. 03110 p Measurement of thermodynamics with various methods. p All results are in good agreement. p But, non-negligible discrepancy at T/Tc≈1 -1. 3?

Luscher, 2013 Makino, Suzuki, 2014 Taniguchi+ (WHOT) 2016; 2017 p Not “gradient” flow but a “diffusion” equation. p Divergence in field renormalization of fermions. p All observables are finite at t>0 once Z(t) is fixed.

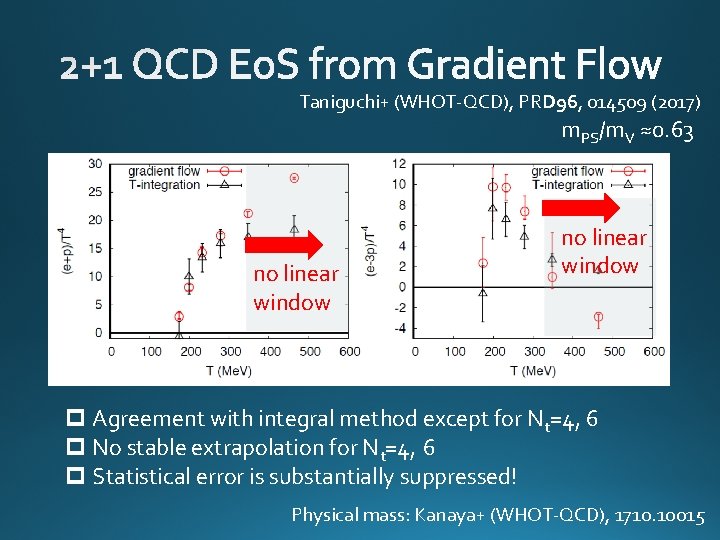
Taniguchi+ (WHOT-QCD), PRD 96, 014509 (2017) m. PS/m. V ≈0. 63 no linear window p Agreement with integral method except for Nt=4, 6 p No stable extrapolation for Nt=4, 6 p Statistical error is substantially suppressed! Physical mass: Kanaya+ (WHOT-QCD), 1710. 10015

Constructing EMT on the lattice Thermodynamics EMT Correlation Function Stress distribution in qq system ー

p Transport Coefficient Kubo formula viscosity Karsch, Wyld, 1987 Nakamura, Sakai, 2005 Meyer; 2007, 2008 … Borsanyi+, 2018 Astrakhantsev+, 2018 p Energy/Momentum Conservation : t-independent constant p Fluctuation-Response Relations

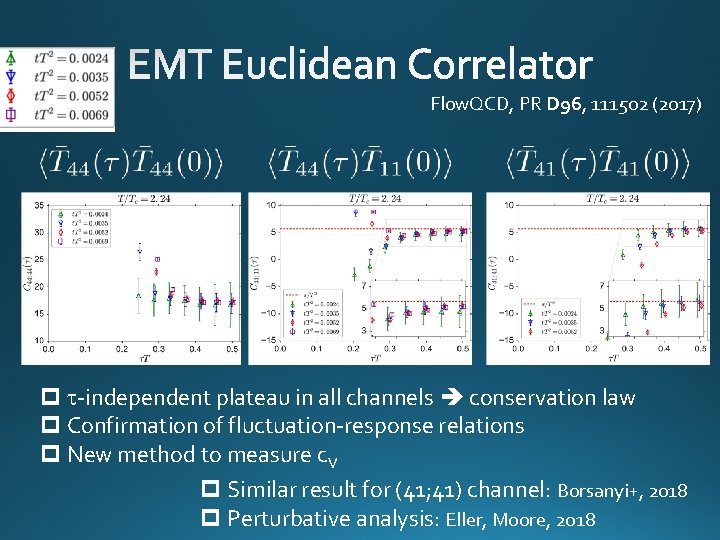
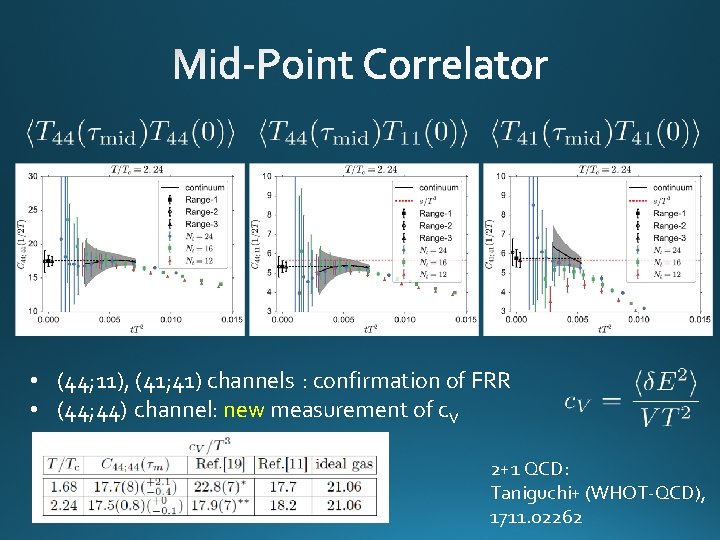
Flow. QCD, PR D 96, 111502 (2017) p t-independent plateau in all channels conservation law p Confirmation of fluctuation-response relations p New method to measure c. V p Similar result for (41; 41) channel: Borsanyi+, 2018 p Perturbative analysis: Eller, Moore, 2018

Constructing EMT on the lattice Thermodynamics EMT Correlation Function Stress distribution in qq system ー

Pressure S

Pressure Generally, F and n are not parallel S In thermal medium elastic body v fluid S F S Stress Tensor Landau Lifshitz

Action-at-a-distance Newton 1687 Local interaction Faraday 1839

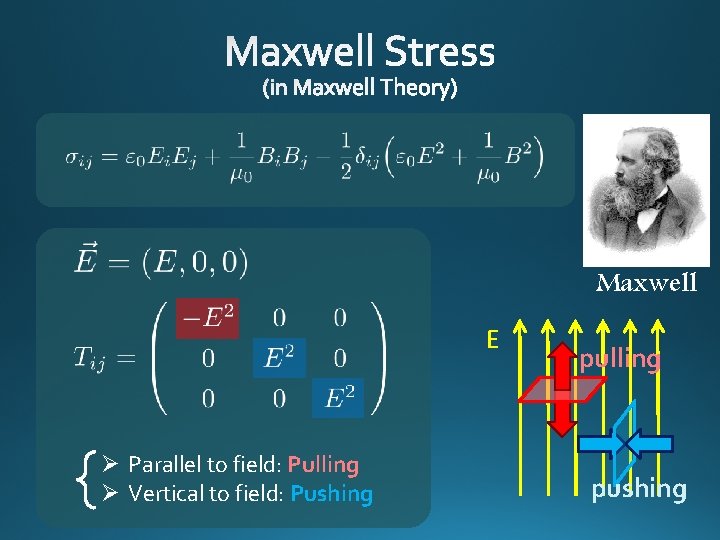
Maxwell E Ø Parallel to field: Pulling Ø Vertical to field: Pushing pulling pushing

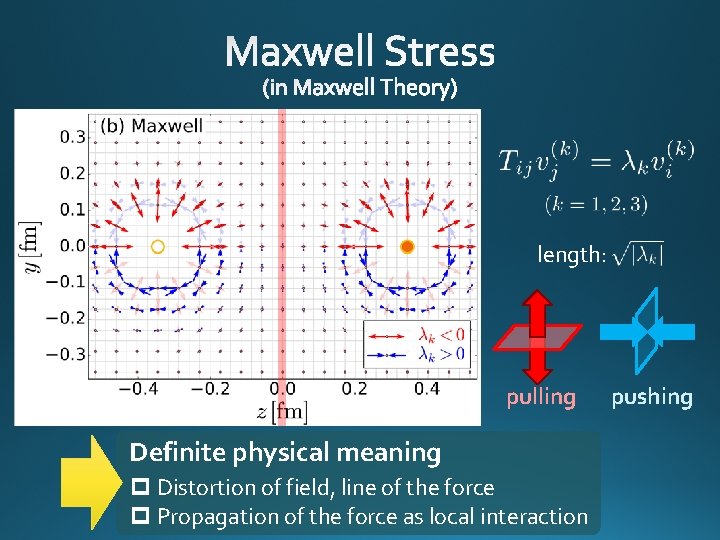
length: pulling Definite physical meaning p Distortion of field, line of the force p Propagation of the force as local interaction pushing

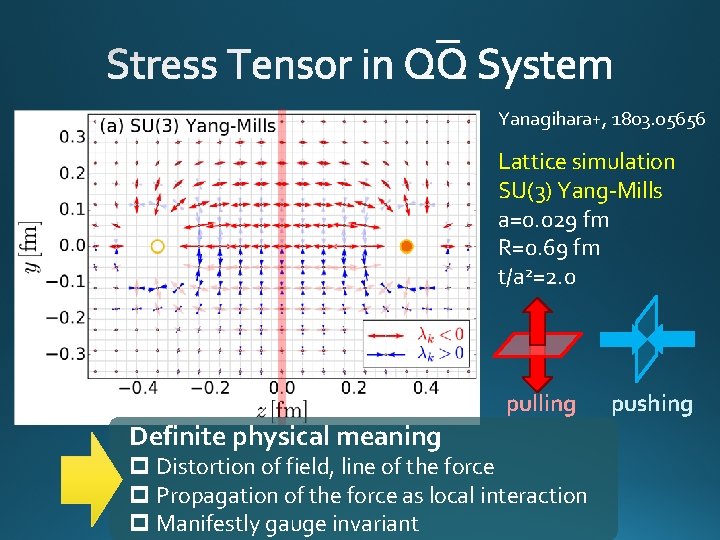
ー Yanagihara+, 1803. 05656 Lattice simulation SU(3) Yang-Mills a=0. 029 fm R=0. 69 fm t/a 2=2. 0 pulling Definite physical meaning p Distortion of field, line of the force p Propagation of the force as local interaction p Manifestly gauge invariant pushing

p SU(3) Yang-Mills (Quenched) p Wilson gauge action p Clover operator p APE smearing / multi-hit p fine lattices (a=0. 029 -0. 06 fm) p continuum extrapolation p Simulation: bluegene/Q@KEK Yanagihara+, 1803. 05656 R=0. 92 fm R=0. 69 fm R=0. 46 fm

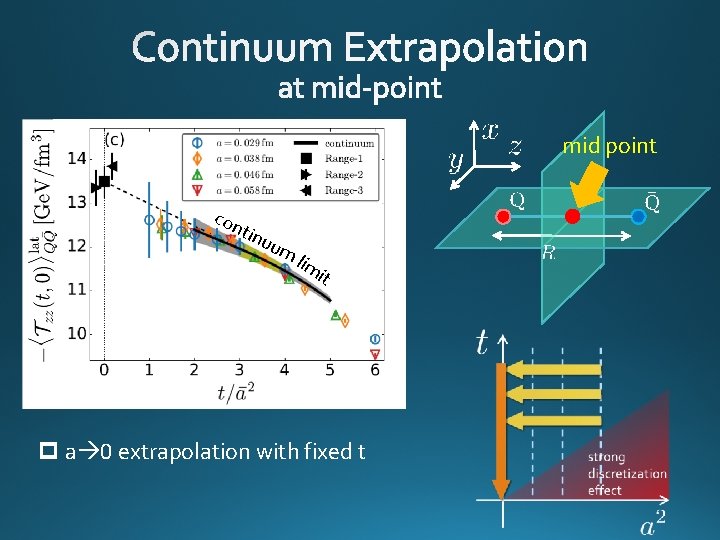
mid point con t inu um lim it p a 0 extrapolation with fixed t

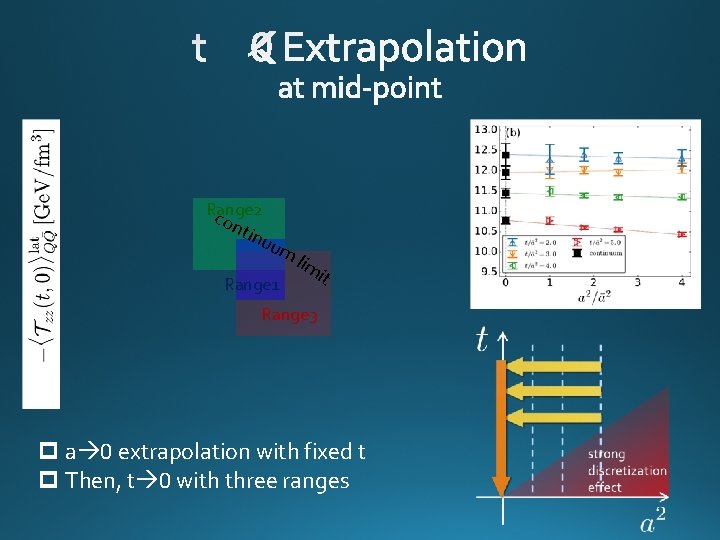
Range 2 c ont inu um Range 1 lim it Range 3 p a 0 extrapolation with fixed t p Then, t 0 with three ranges

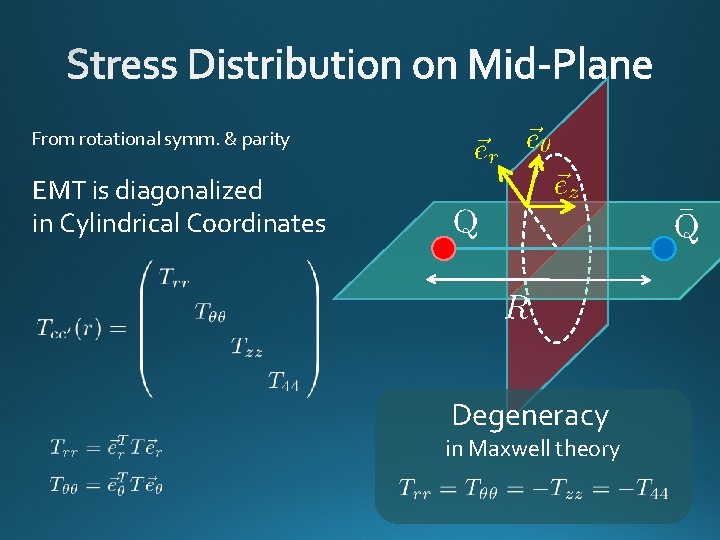
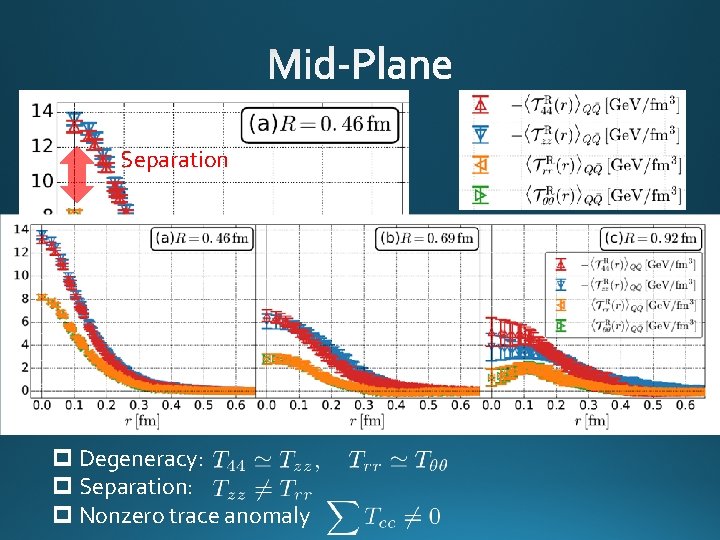
From rotational symm. & parity EMT is diagonalized in Cylindrical Coordinates Degeneracy in Maxwell theory

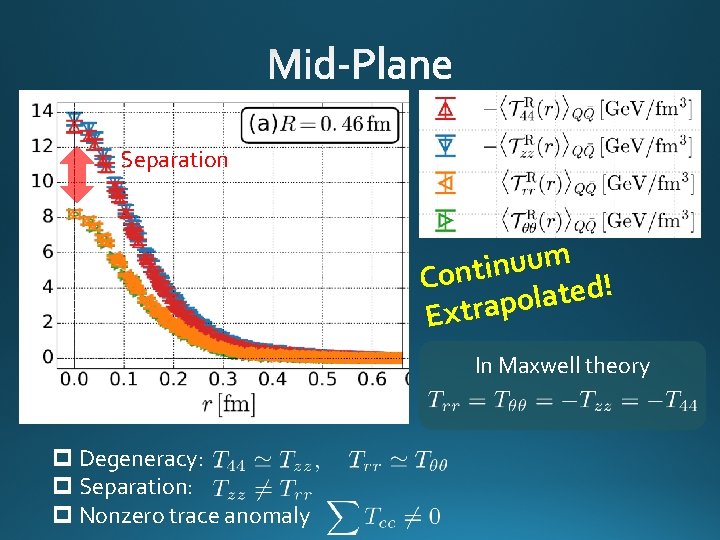
Separation m u u n i t Con ! d e t a l o p a r t Ex In Maxwell theory p Degeneracy: p Separation: p Nonzero trace anomaly

Separation m u u n i t Con ! d e t a l o p a r t x E p Degeneracy: p Separation: p Nonzero trace anomaly

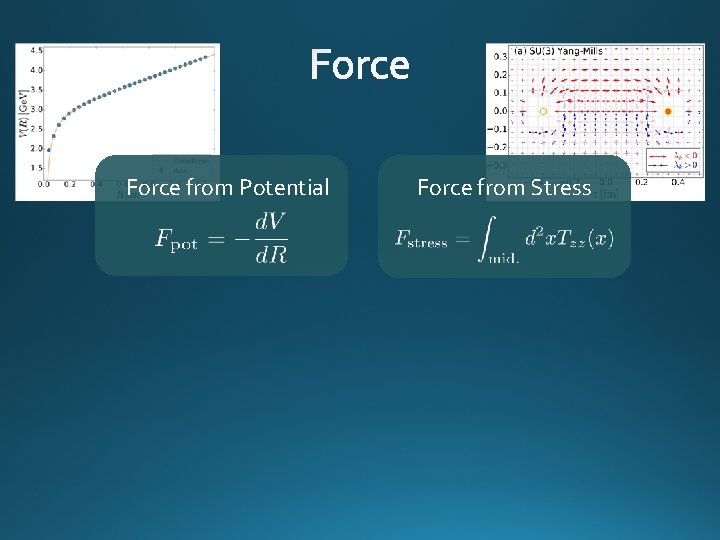
Force from Potential Force from Stress

Force from Potential Newton 1687 Force from Stress Faraday 1839

Force from Potential Force from Stress ! t n e m e e r Good Ag Newton 1687 Faraday 1839

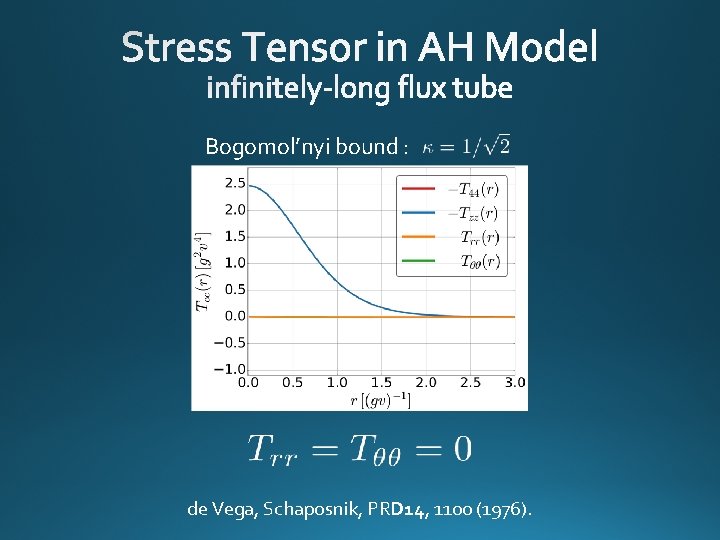
Yanagihara, Iritani, MK, in prep. Abelian-Higgs Model GL parameter: p type-II : p Bogomol’nyi bound : Infinitely long tube p degeneracy Luscher, 1981 p momentum conservation

Bogomol’nyi bound : de Vega, Schaposnik, PRD 14, 1100 (1976).

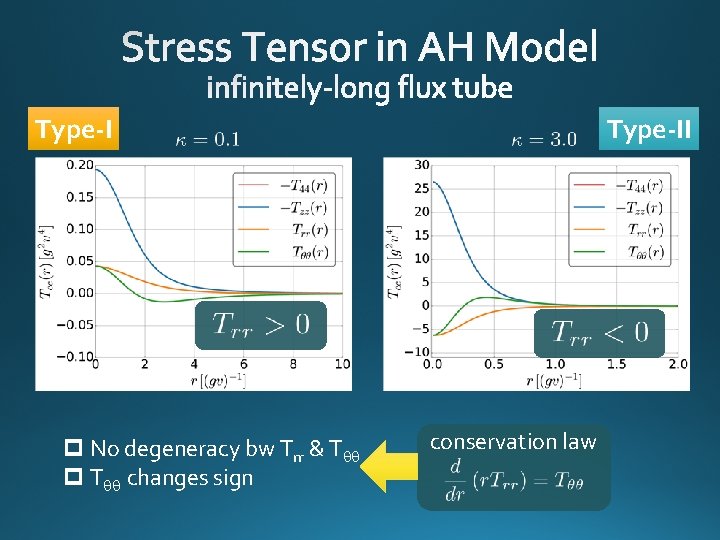
Type-I p No degeneracy bw Trr & Tqq p Tqq changes sign Type-II conservation law

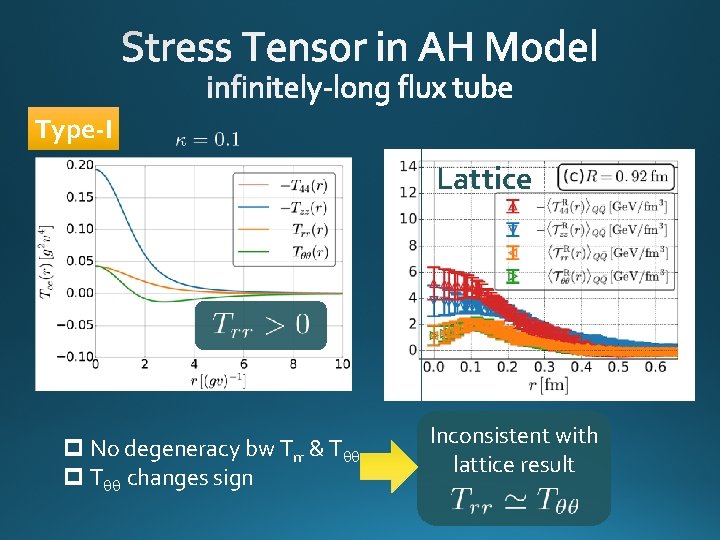
Type-I Lattice p No degeneracy bw Trr & Tqq p Tqq changes sign Inconsistent with lattice result

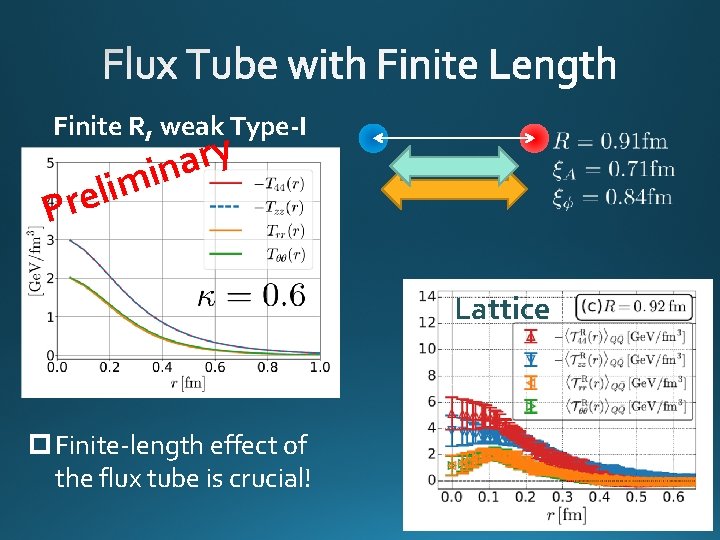
Finite R, weak Type-I y r a n i im l e r P Lattice p Finite-length effect of the flux tube is crucial!

p The analysis of energy-momentum tensor on the lattice is now available, and various stuides are ongoing! p gradient flow method p determination of Z 6, Z 3, Z 1 / multilevel algorithm Stress Thermodynamics Correlation Functions

p The analysis of energy-momentum tensor on the lattice is now available, and various stuides are ongoing! p gradient flow method p determination of Z 6, Z 3, Z 1 / multilevel algorithm Stress Thermodynamics Correlation Functions p. So many future studies p Flux tube at nonzero temperature p EMT distribution inside hadrons p viscosity / other operators / instantons / full QCD

p p Expectation values of Tmn SU(3) YM theory Wilson gauge action Parameters: • Nt = 12, 16, 20 -24 • aspect ratio 5. 3<Ns/Nt<8 • 1500~2000 configurations p Scale from gradient flow Flow. QCD, 1503. 06516 Flow. QCD, PRD 94, 114512 (2016)

• (44; 11), (41; 41) channels : confirmation of FRR • (44; 44) channel: new measurement of c. V 2+1 QCD: Taniguchi+ (WHOT-QCD), 1711. 02262

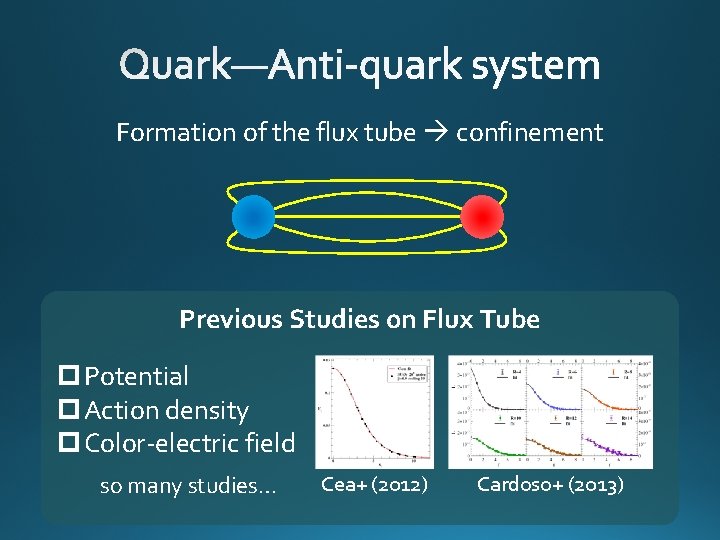
Formation of the flux tube confinement Previous Studies on Flux Tube p Potential p Action density p Color-electric field so many studies… Cea+ (2012) Cardoso+ (2013)

SU(3) Yang-Mills (quantum) Maxwell (classical) Propagation of the force is clearly different in YM and Maxwell theories!

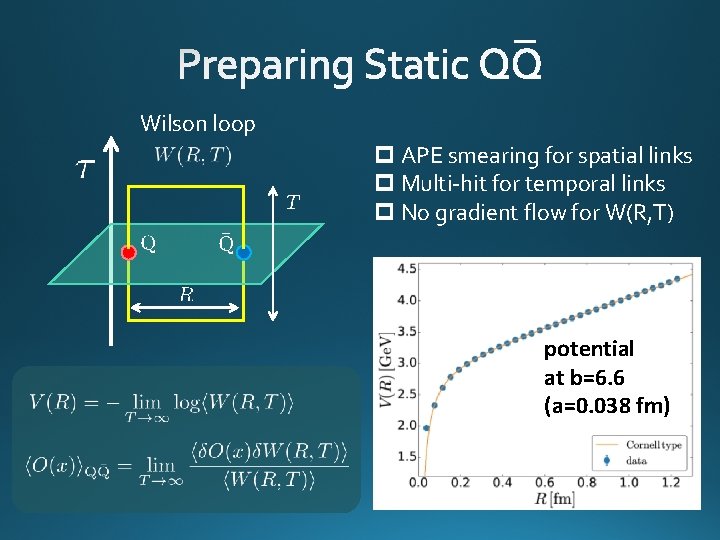
Wilson loop p APE smearing for spatial links p Multi-hit for temporal links p No gradient flow for W(R, T) potential at b=6. 6 (a=0. 038 fm)

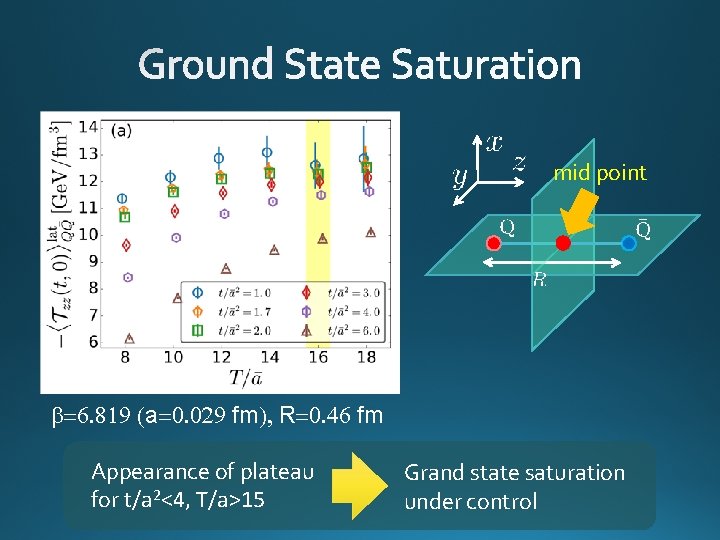
mid point b=6. 819 (a=0. 029 fm), R=0. 46 fm Appearance of plateau for t/a 2<4, T/a>15 Grand state saturation under control

t/a 2=1. 0 t/a 2=3. 0 Wilson loop t/a 2=4. 0 b=6. 819 (a=0. 029 fm), R=0. 46 fm Appearance of plateau for t/a 2<4, T/a>15 Grand state saturation under control

Abelian-Higgs Model GL parameter: p type-II : p Bogomol’nyi bound : Infinitely long tube p degeneracy Luscher, 1981 p conservation law