Xavier Granier Least Squares Fitting FiniteDimensional Vector Spaces

































































- Slides: 82

Xavier Granier -- Least Squares Fitting – Finite-Dimensional Vector Spaces “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

General considerations on objectives “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Data approximation and analysis § Data from real measurements – How to use them in simulation / rendering ? ─ Ex: acquired point clouds for geometry [Chen et al. – CGF 2013] FP 8: Surfaces II Auditorium Schweitzer - Wednesday - 10: 40 - 12: 20 “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Data approximation and analysis § Data from real measurements – How to use them in simulation / rendering ? – How to study the general behavior ? ─ Ex: data extrapolation in statistics 0. 8 0. 6 0. 4 Series 1 0. 2 Poly. (Series 0) 0 0 1 2 3 4 5 6 -0. 2 -0. 4 “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

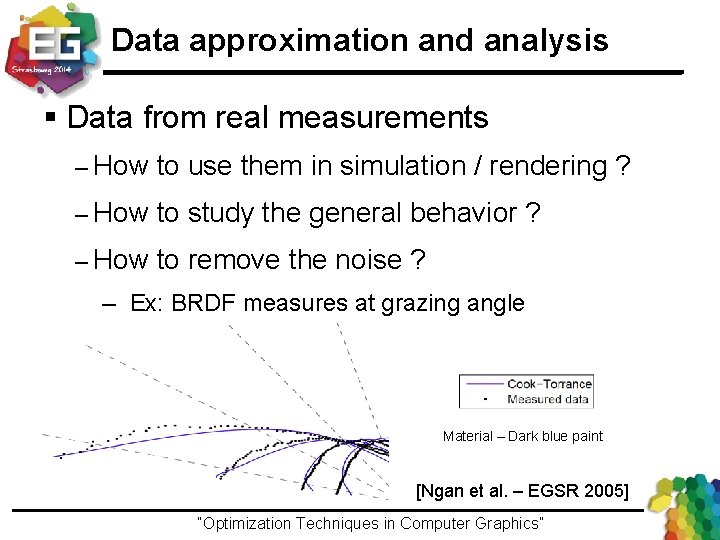
Data approximation and analysis § Data from real measurements – How to use them in simulation / rendering ? – How to study the general behavior ? – How to remove the noise ? ─ Ex: BRDF measures at grazing angle Material – Dark blue paint [Ngan et al. – EGSR 2005] “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

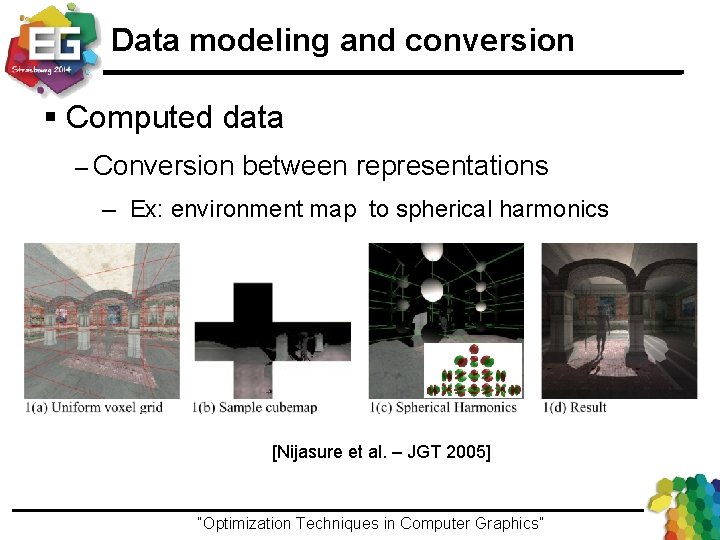
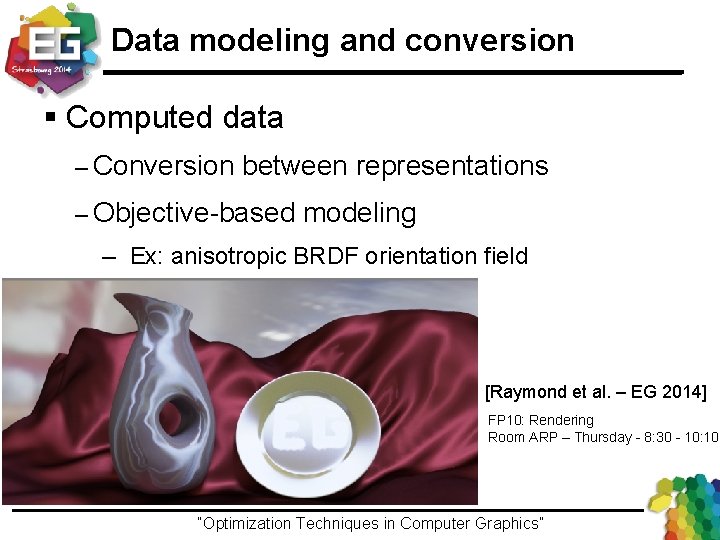
Data modeling and conversion § Computed data – Conversion between representations ─ Ex: environment map to spherical harmonics [Nijasure et al. – JGT 2005] “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Data modeling and conversion § Computed data – Conversion between representations – Objective-based modeling ─ Ex: anisotropic BRDF orientation field [Raymond et al. – EG 2014] FP 10: Rendering Room ARP – Thursday - 8: 30 - 10: 10 “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Generalized Goal § Finding the best approximation – Given a numerical model – Using a reduce set of parameters § Ex: linear regression ( x 3 , y 3 ) ( x 5 , y 5 ) y = ax + b ( x 6 , y 6 ) ( x 7 , y 7 ) ( x 1 , y 1 ) ( x 4 , y 4 ) ( x 2 , y 2 ) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Definition of “Best” § Maximize the quality – Ex: expectation maximization § Be as close as possible to the goal – – Need a notion of distance / norm To be minimized “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Definitions § Norm – Separate points – Absolute homogeneity – Triangle inequality § Distance “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Euclidian Norm for Least Squares § Based on standard dot product § Error » average distance – Uniform weight for each dimension “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Euclidian Norm for Least Squares ● Generalized dot product – W: symmetric positive definite matrix ● Error » weighted average distance – W is a diagonal matrix “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Other: max norm § Maximum of absolute values § Largest error “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

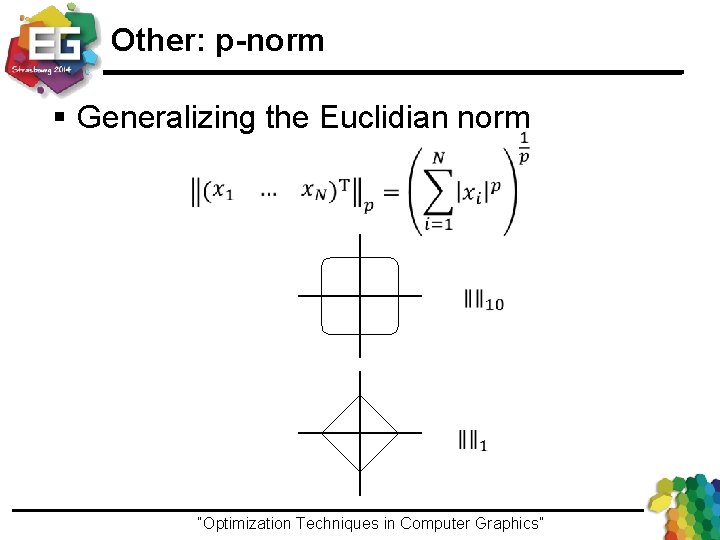
Other: p-norm § Generalizing the Euclidian norm “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Linear Optimization Least Squares “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Linear optimization § M measured data § Linear approximating function – Parameters: v – Linear combination of basis function: fk – 2 D example: 2 D line y = ax + b “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Least Squares § Minimize Euclidian error = objective § Unique solution if well conditioned – Do not contain the trivial solution v = 0 ● Example: implicit line – – Measures parameters: M K Measures are different “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Solving Linear Least Squares ● Properties of the objective function – – – ● Positive Quadratic Parabola Minimum when gradient = 0 ● Lead to a linear system to solve “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Demonstration 1 D “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

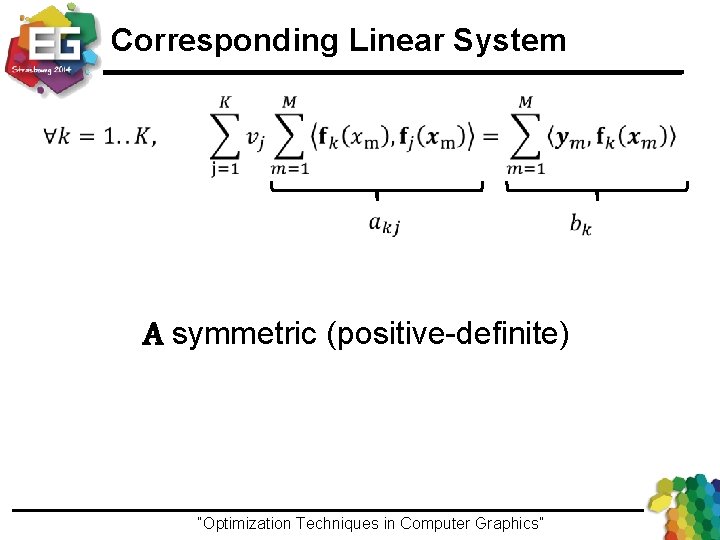
Corresponding Linear System A symmetric (positive-definite) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Demonstration ND “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Corresponding Linear System A symmetric (positive-definite) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Equivalent Linear System § Minimal least squares error – Equivalent linear system – – A symmetric If well conditioned, A positive-definite § How to solve it ? – – Use your favorite linear algebra solver Ex: Cholesky factorization “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Conditioning of a linear system § Conditioning = stability of a system – Input: x (perturbation x + dx) – Output: v (perturbation v + dv) – Relative conditioning ● Smaller is better § For a linear system – Conditioning of the matrix – Symmetric positive-definite matrix ● Ratio of eigenvalues “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Adding constraints § For regularization – – Improvement on conditioning Removing trivial solution ● Example of implicit line “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Adding constraints § For regularization Improvement on conditioning Removing trivial solution – – ● Example of implicit line “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Adding constraints § For regularization Improvement on conditioning Removing trivial solution – – ● Example of implicit line § Other linear constraints – Ex: continuity, … (cf. geometry part) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Lagrange Multipliers § Approach – – – Original objective A new constraint New objective § Minimum is reached when “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Equivalent Linear System § If multiple linear constraints § New objective function § Unique solution if it exists – But matrix may not be symmetric ● Cf. geometry part of the tutorial “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Linear Least Squares - Summary ● Avantages – Euclidian norm : in average the best ● – – Linear system to solve : unique solution Extensions ● ● ● Robust to noise Non-uniform norm Linear constraints as equalities But – – Minimizing maximal error ? Inequality linear constraints ? “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Linear Optimization Linear/Quadratic Programming “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Inequality constraints § For regularization Improvement on conditioning Removing trivial solution – – ● Example of implicit line § Other linear constraints – – Ex: continuity, … (cf. geometry part) Definition domain (see BRDF fitting) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Linear Programing § Minimizing the max-norm § Toward linear programing “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

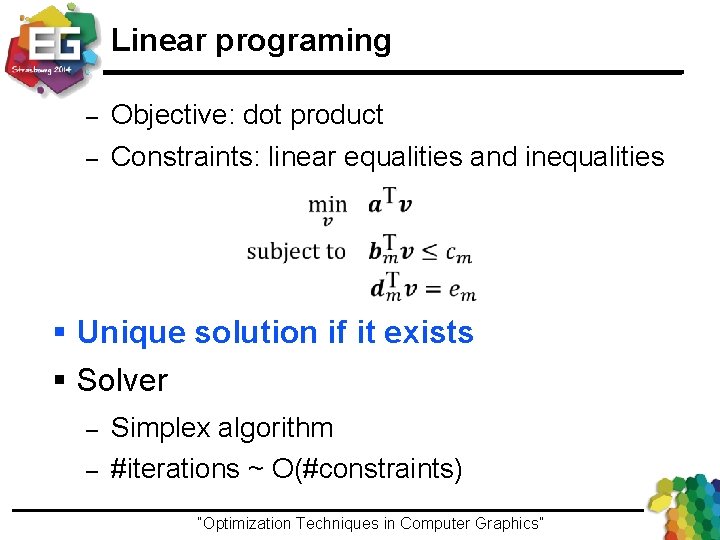
Linear programing – – Objective: dot product Constraints: linear equalities and inequalities § Unique solution if it exists § Solver – – Simplex algorithm #iterations ~ O(#constraints) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Simplex: Standard Form “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

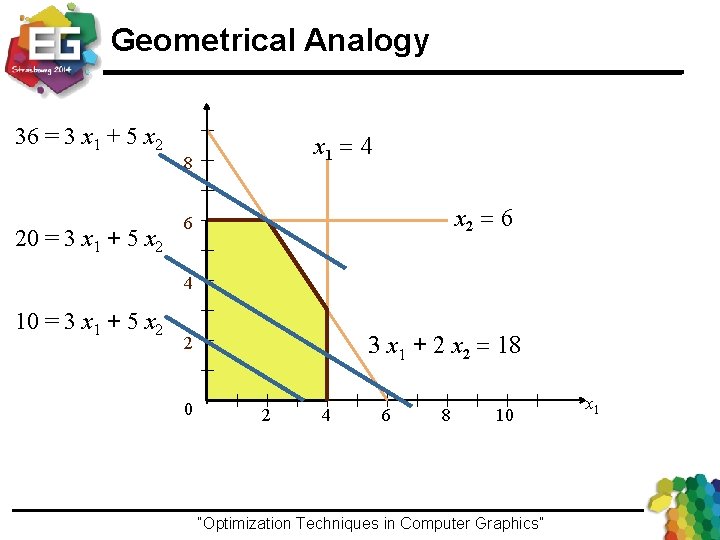
Geometrical Analogy Maximize Constraints x 2 6 3 x 1 + 5 x 2 x 1 4 3 x 1 + 2 x 2 18 x 1 0 x 2 0 “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Geometrical Analogy x 2 36 = 3 x 1 + 5 x 2 20 = 3 x 1 + 5 x 2 x 1 = 4 8 x 2 = 6 6 4 10 = 3 x 1 + 5 x 2 3 x 1 + 2 x 2 = 18 2 0 2 4 6 8 10 x 1 “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Quadratic Programing § Term to minimize = quadratic form § Iterative solver – Classical least squares solver ● – Langrage multiplier for equalities If some inequalities are not fulfilled ● Take one and transform it into an equality § Unique solution if it exists “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

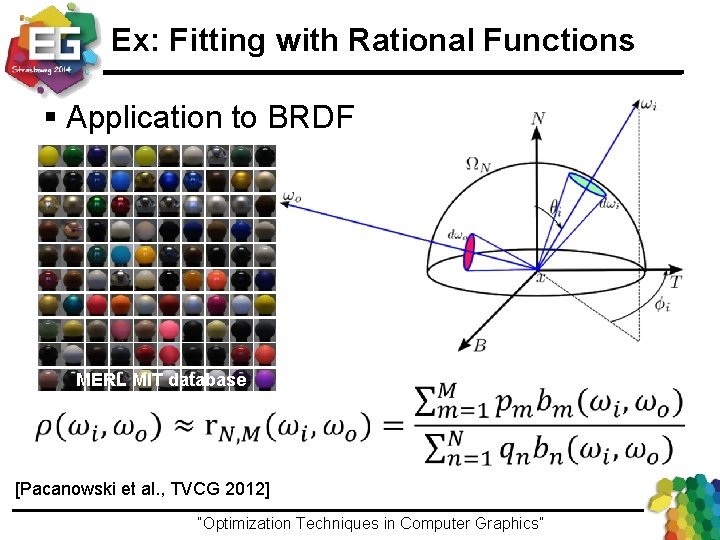
Ex: Fitting with Rational Functions § Application to BRDF MERL MIT database [Pacanowski et al. , TVCG 2012] “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

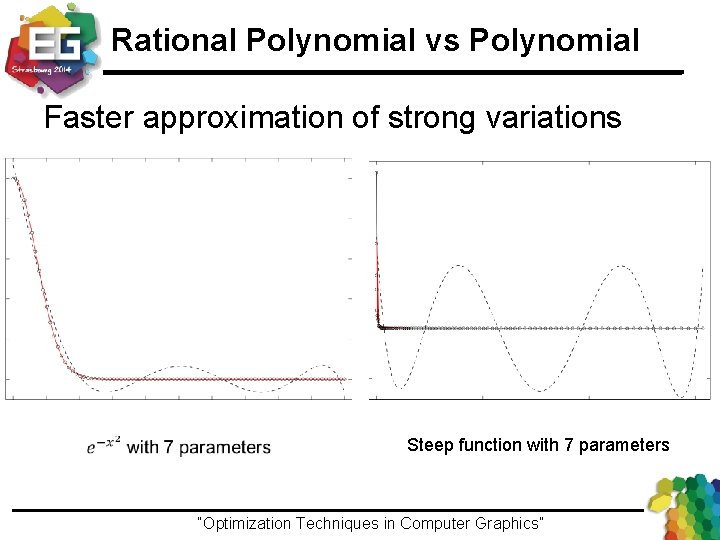
Rational Polynomial vs Polynomial Faster approximation of strong variations Steep function with 7 parameters “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Approximation with Rational Functions § Specialized linear methods – DCA: Simplex ─ Improvement by [Papamarkos 1988] è Free-pole solution è Numerical stability § New method based on vertical-segment [Celis et al. 2007] “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Vertical Segments Find the most stable rational function such as Equivalent to a convex quadratic optimization problem “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Benefits of this approach § Unique solution if it exists § Pole-free § Limit case = interpolation scheme § Easy integration of additional constraints: – Symmetry – Positivity – Monotonicity (positive derivative) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Accurate Approximation of BRDF Original Data 99 MB Approximation 1, 7 k. B “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

ALTA Library § Open-source C++ Library • For model comparison (fitting & approximation) § Plugin mechanism • Easy to extend • Interaction with BRDF Explorer § Alpha version http: //alta. gforge. inria. fr/ • Open format for data (MERL, ASTM) • Non-linear approximation • Rational functions • Analytical models of BRDF • Scripting mechanism for automatic fitting Levenberg Marquardt CUre T MERL Ward Lafortune [Belcour et al, Inria Technical Report, 2013] “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Non-Linear Optimization “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Linear vs Non-linear approximation § Linear: – Global Convergence – Limited expressivity § Non-linear: – Local Convergence – More powerful expressivity “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Non-linear Optimization § When it is impossible to use – Linear combination of functions – Linear / quadratic objective function – Linear constraints § Solvers are iterative – Step by step progression toward a solution – Still where gradient is null Convergence toward a local minima ● ● ● Not a unique solution If a unique solution exists, it will be found “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Non-linear approximation § Local convergence – Conjugate gradient methods – Levenberg-Marquardt –… Local minimum Global minimum “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

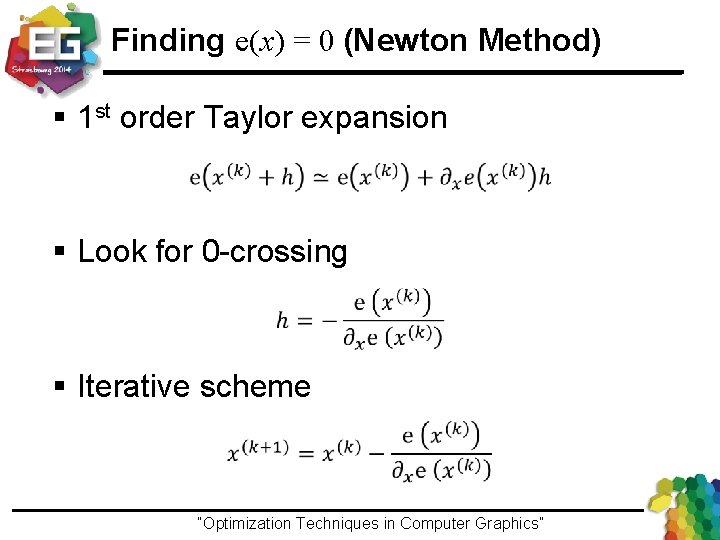
Finding e(x) = 0 (Newton Method) § 1 st order Taylor expansion § Look for 0 -crossing § Iterative scheme “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

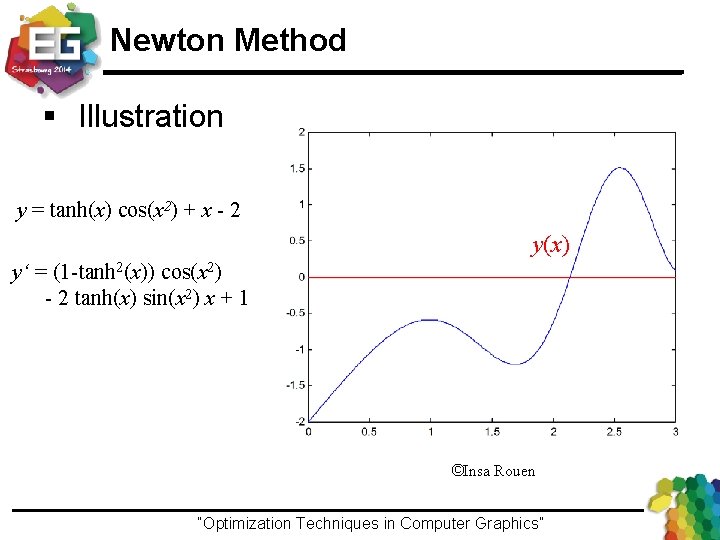
Newton Method § Illustration y = tanh(x) cos(x 2) + x - 2 y(x) y‘ = (1 -tanh 2(x)) cos(x 2) - 2 tanh(x) sin(x 2) x + 1 ©Insa Rouen “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Newton Method § Illustration x 2= 2. 1380 y = tanh(x) cos(x 2) + x - 2 x 1 = 2. 1627 y‘ = (1 -tanh 2(x)) cos(x 2) - 2 tanh(x) sin(x 2) x + 1 x 0 = 2 x 1 = 2. 1627 x 2 = 2. 1380 x 3 = 2. 1378 x 4 = 2. 1378 x 0 = 2 ©Insa Rouen “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Newton Method: convergence § Quadratic convergence ● Conditions – Known analytic derivative – Tangent crosses 0 -line in the definition domain. “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

1 D Optimization – e'(x) = 0 § 2 nd order Taylor expansion § 0 -crossing of derivative § Similar iterative process “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

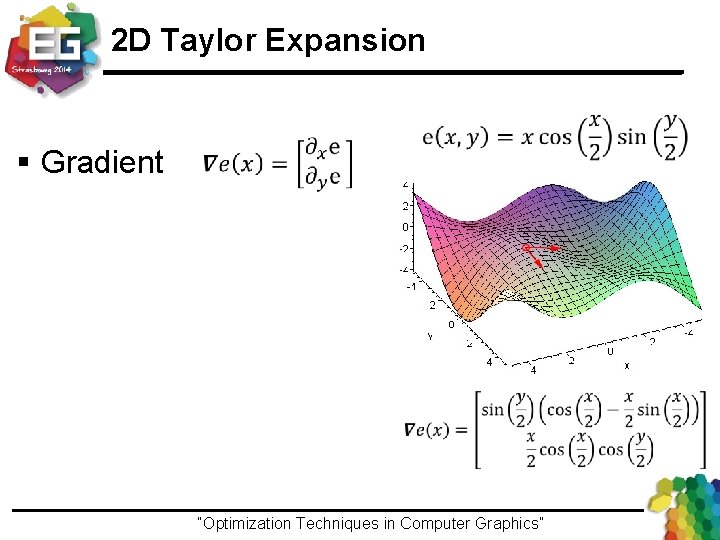
2 D Taylor Expansion “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

2 D Taylor Expansion § Gradient “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

2 D Taylor Expansion § Gradient § 1 st order derivative – Dot product with direction “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

N-dimensional Expansion § 1 equation, N unknowns gradient Hessian Matrix “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

N-dimensional Expansion § 1 equation, N unknowns gradient Hessian Matrix = 2 D Tensor “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Hessian Matrix § 2 D Tensor – Associated to a quadratic form § Symmetric – – Schwarz’ theorem If a function has continuous nth-order partial derivative, derivation order has no influence on the result. “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Derivatives in Dimension Nx. M § M equations, N unknowns Jacobian matrix “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Jacobian Matrix § Be careful: 1 st order derivative only – – Gradient for vector functions Not a Hessian matrix § Used for integration by substitution – – e is a bijective vector function N = M (square matrix) “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Optimization: find Ñe(x) = 0 § 2 nd order Taylor expansion § Step estimation § Iteration “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Limitation of Newton Method ● If the Hessian is not semi positive-definite – Each step increase the error ! “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

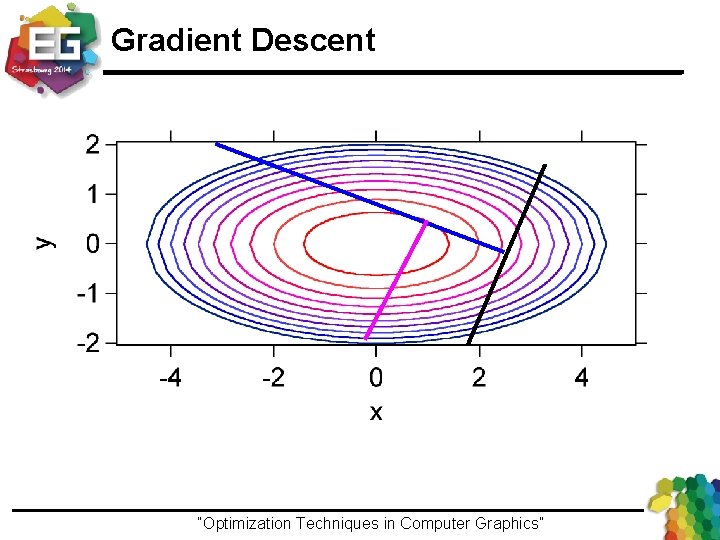
Gradient Descent § Follow the inclination of the function – Inclination = slope = gradient § Compute how much in this direction “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Gradient Descent “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Gradient Descent : Convergence ● K: condition number of the Hessian – Convergence ● Starting point is very important – ● As close as possible to the solution Remaining question – What is the best direction ? “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

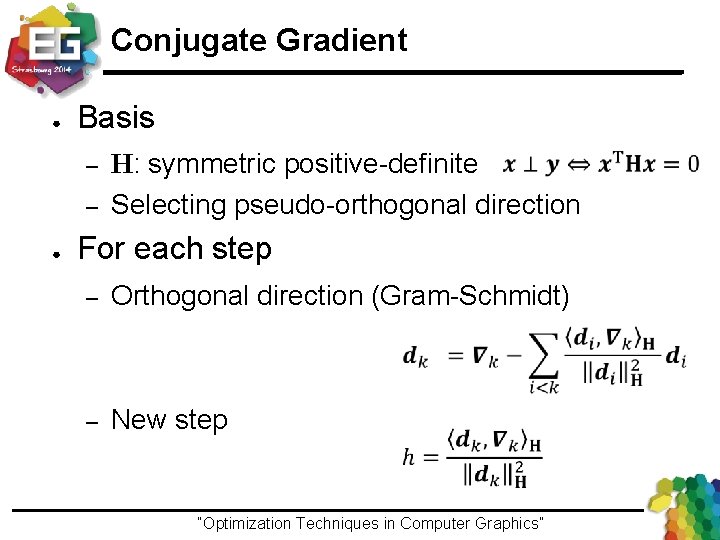
Conjugate Gradient ● Basis – – ● H: symmetric positive-definite Selecting pseudo-orthogonal direction For each step – Orthogonal direction (Gram-Schmidt) – New step “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Convergences § K: condition number of the Hessian § Gradient descent § Conjugate gradient § Limitation: needs 2 nd order derivatives “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Residual-based form (ex: matlab) § Residual § Least-Square objective § Gradient “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Residual-based form § Residual § Least-Square objective § Gradient § Hessian matrix “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Gauss-Newton Method § Idea: replacing the Hessian matrix § Advantages – – No 2 nd derivatives Semi positive-definite matrix § Limitations – – Valid approximation for small residual Careful choice of initial values “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Levenberg-Marquardt § Most used method § For each iteration, direction is § Choice of l is balancing the behavior – – Small: Newton Large: fast gradient descent § More robust to noise “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Input data and Co-variance Coming back to stability “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Reminder: Least Squares § Minimize Euclidian error = objective § Unique solution if well conditioned – Do not contain the trivial solution v = 0 ● Example: implicit line – – Measures parameters: M K Measures are different “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

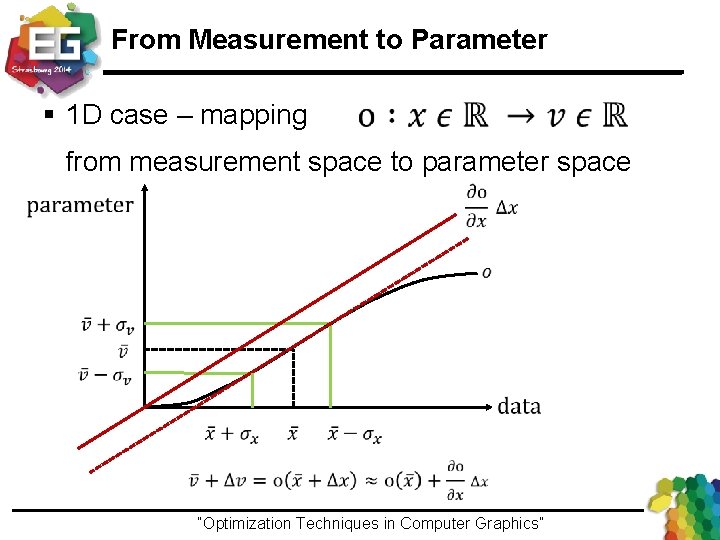
From Measurement to Parameter § 1 D case – mapping from measurement space to parameter space “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

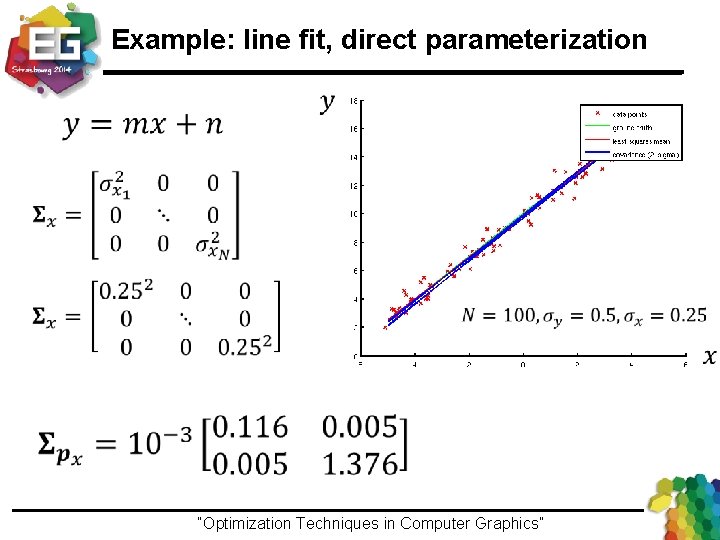
Example: line fit, direct parameterization - Measurements - Parameter vector - Fitting linear system “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Example: line fit, direct parameterization - Measurements - Parameter vector ground truth LS fit - Fitting linear system - Least Square solution Ground truth values: “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Example: line fit, direct parameterization “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Example: line fit, direct parameterization “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

Example: line fit, direct parameterization with 95% certainty “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013

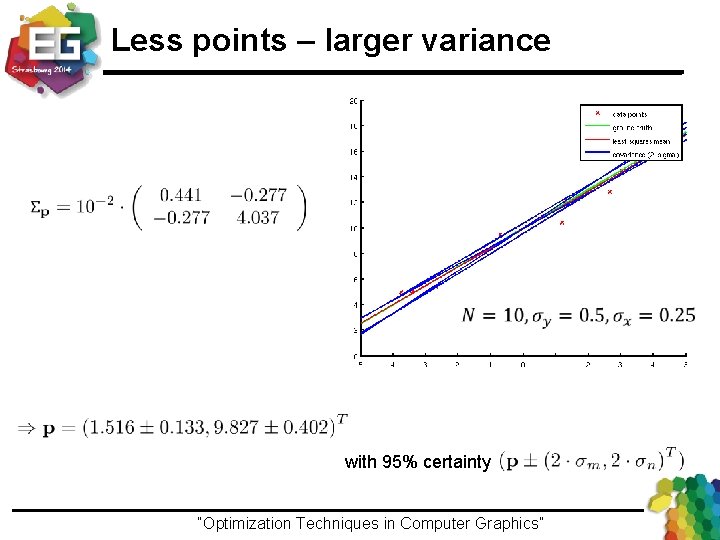
Less points – larger variance with 95% certainty “Optimization Techniques in Computer Graphics”Ivo Ihrke / Winter 2013
 Youcubed squares and more squares answers
Youcubed squares and more squares answers My age
My age Definition of vector space
Definition of vector space Left multiplication transformation
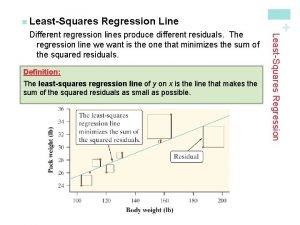
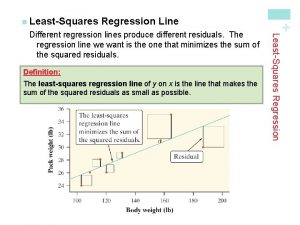
Left multiplication transformation Least squares regression line
Least squares regression line Least squares regression line minitab
Least squares regression line minitab Lms cis
Lms cis Continuous least squares approximation
Continuous least squares approximation Recursive least square method
Recursive least square method Least squares regression line definition
Least squares regression line definition Ordinary least squares
Ordinary least squares Least square solution
Least square solution Fit least squares jmp
Fit least squares jmp Recursive least squares python
Recursive least squares python Properties of least square estimators
Properties of least square estimators Least square solution
Least square solution Least squares regression line definition
Least squares regression line definition What are the principles of least squares
What are the principles of least squares Qr factorization least squares
Qr factorization least squares Eviews training
Eviews training Constrained least square filtering
Constrained least square filtering Least squares regression
Least squares regression The least square method
The least square method Regression berlin
Regression berlin How to find least squares regression line on statcrunch
How to find least squares regression line on statcrunch Bivariate least squares regression
Bivariate least squares regression Segmented least squares dynamic programming
Segmented least squares dynamic programming Www.whfreeman/tps5e
Www.whfreeman/tps5e Nonlinear regression lecture notes
Nonlinear regression lecture notes Vector unitario
Vector unitario Vector resolution
Vector resolution Define a position vector
Define a position vector Directed line segment math definition
Directed line segment math definition Fitting equations to data
Fitting equations to data Spline pin
Spline pin Butler system heat exchanger
Butler system heat exchanger Matlab sine fitting
Matlab sine fitting Conduit layout drawing
Conduit layout drawing Primordial nucleosynthesis
Primordial nucleosynthesis Curve fitting with polynomial models
Curve fitting with polynomial models Matlab parameter estimation
Matlab parameter estimation Curve fitting matlab
Curve fitting matlab Curve fitting with linear models
Curve fitting with linear models Quadratic spline interpolation matlab
Quadratic spline interpolation matlab Curve fitting with exponential and logarithmic models
Curve fitting with exponential and logarithmic models W&w glass systems
W&w glass systems A/c fitting size chart
A/c fitting size chart Curve fitting with linear models
Curve fitting with linear models Quadratic curve fitting
Quadratic curve fitting Transformer fittings and accessories
Transformer fittings and accessories Curve fitting techniques
Curve fitting techniques Castan golf
Castan golf Gaussian curve fitting
Gaussian curve fitting Steer clipping and fitting techniques
Steer clipping and fitting techniques Professional shoe fitting
Professional shoe fitting Fitting into society
Fitting into society Labview curve fitting
Labview curve fitting How to approximate the best fitting line for data
How to approximate the best fitting line for data Curve fitting with quadratic models
Curve fitting with quadratic models Xavier mail delivery robot
Xavier mail delivery robot Xavier seiso
Xavier seiso Mdvpn
Mdvpn Xavier bonilla
Xavier bonilla Xavier van rooyen
Xavier van rooyen Xavier amaro
Xavier amaro François xavier saluden
François xavier saluden Lleiva
Lleiva Rafael de vasconcelos xavier ferreira
Rafael de vasconcelos xavier ferreira Xavier fernando
Xavier fernando Xavier zanchi
Xavier zanchi Francisco xavier medium
Francisco xavier medium Mehek fin
Mehek fin Xavier pico
Xavier pico Xavier gabilly
Xavier gabilly Johan xavier
Johan xavier Xavier naidoo rausammy naidoo
Xavier naidoo rausammy naidoo Who killed mr xavier answer key
Who killed mr xavier answer key Minera san xavier
Minera san xavier Xavier barberis
Xavier barberis Antes de morrer quero o ceu cem por cento
Antes de morrer quero o ceu cem por cento Xavier martorell
Xavier martorell Mr xavier mystery claim evidence reasoning
Mr xavier mystery claim evidence reasoning Xavier pansaers
Xavier pansaers