Wykad 6 Metody Monte Carlo Metody Monte Carlo

Wykład 6 Metody Monte Carlo

Metody Monte Carlo Najszerzej: są to metody oparte na wykorzystaniu liczb losowych do rozwiązania określonego problemu obliczeniowego.

Podstawowe pojęcia teorii prawdopodobieństwa: • Zdarzenie elementarne jest to możliwy wynik doświadczenia losowego, zwykle przypisane jest jemu pewne prawdopodobieństwo wystąpienia. • Prawdopodobieństwo jest to funkcja P(X), która przyporządkowuje każdemu elementowi zbioru zdarzeń losowych pewną nieujemną wartość rzeczywistą.

Definicje prawdopodobieństwa: Definicja klasyczna (Laplace'a) w roku 1812. Prawdopodobieństwem zajścia zdarzenia A nazywamy iloraz liczby zdarzeń sprzyjających zdarzeniu A do liczby wszystkich możliwych przypadków, zakładając, że wszystkie przypadki wzajemnie się wykluczają i są jednakowo możliwe. Definicja częstościowa: gdzie kn(A) to liczba rezultatów sprzyjających zdarzeniu A po n próbach.

Prawdopodobieństwo zajścia zdarzenia A możemy zapisać w postaci: gdzie |A| oznacza liczbę elementów zbioru A, zaś |Ω| liczbę elementów zbioru Ω. Przykład: Rzucamy sześcienną kostką. Jakie jest prawdopodobieństwo, że liczba oczek będzie większa od 5? Zbiór zdarzeń elementarnych Ω = {1, 2, 3, 4, 5, 6}, zatem liczba możliwych zdarzeń |Ω| = 6. Zbiór zdarzeń sprzyjających A = {6}, liczba zdarzeń sprzyjających |A| = 1. Prawdopodobieństwo zajścia zdarzenia wynosi:

Definicje prawdopodobieństwa: Prawdopodobieństwo geometryczne Definicja klasyczna nie pozwala obliczać prawdopodobieństwa w przypadku, gdy zbiory A i Ω są nieskończone, jeśli jednak zbiory te mają interpretację geometryczną, zamiast liczebności zbiorów można użyć miary geometrycznej (długość, pole powierzchni, objętość). Przykład: z przedziału [0, 4] wybieramy losowo punkt. Jakie jest prawdopodobieństwo, że wybrany punkt będzie należał do przedziału [1, 2]? Odpowiedź: Długości przedziałów wynoszą odpowiednio: |[0, 4]| = 4 i |[1, 2]| = 1. Zatem prawdopodobieństwo opisanego zdarzenia wynosi:

Prawdopodobieństwo ma następujące własności: P(Ω) = 1, gdzie Ω jest przestrzenią (zbiorem) zdarzeń elementarnych prawdopodobieństwo sumy przeliczalnego zbioru zdarzeń parami rozłącznych jest równe sumie prawdopodobieństw tych zdarzeń: P(A 1 . . . An . . . ) = P(A 1) +. . . + P(An) +. . . Wartość P(X) nazywa się prawdopodobieństwem zdarzenia X. Ważniejsze własności prawdopodobieństwa: P(A) ≥ 0 P(Ø) = 0 (UWAGA: z P(A)=0 nie wynika, że A=Ø) A B P(A) ≤ P(B) P(A) ≤ 1 A B P(B|A) = 1 P(A) + P(A') = 1, gdzie A′ oznacza zdarzenie losowe przeciwne do A P(A B) = P(A) + P(B) - P(A B).

Rozkład zmiennej losowej X (o wartościach rzeczywistych) jest to prawdopodobieństwo PX określone na zbiorze podzbiorów zbioru liczb rzeczywistych R wzorem: Funkcja gęstości rozkładu Jeżeli istnieje funkcja f taka, że to zmienną X nazywamy zmienną typu ciągłego. Mamy wtedy: Funkcję f nazywamy funkcją gęstości rozkładu zmiennej X. Funkcję P nazywamy dystrybuantą rozkładu losowego

Rozkład Boltzmanna k. B (stała Boltzmanna) = 1. 38´ 10 -23 J/K NAk. B = R (uniwersalna stała gazowa) = 8. 3143 J/(mol´K) q – położenia; p – pędy; w(E) – gęstość stanów o energii E

Początki: prawdopodobnie starożytność Pierwsze udokumentowane użycie: G. Comte de Buffon (1777) obliczenia całki przez rzucanie igły na poziomą płaszczyznę pokrytą równoległymi liniami prostymi. Pierwsze zastosowanie na wielką skalę: J. von Neumann, S. Ulam, N. Metropolis, R. P. Feynman i in. (lata 1940 -te; projekt Manhattan) obliczenia rozpraszania i absorpcji neutronów. Nazwa , , Monte Carlo” została wymyślona jako kryptonim dla tego typu rachunków i odpowiednich metod matematycznych.

Zgrubny podział metod Monte Carlo q Metoda von Neumanna q Metoda Metropolisa (łańcuchów Markowa)

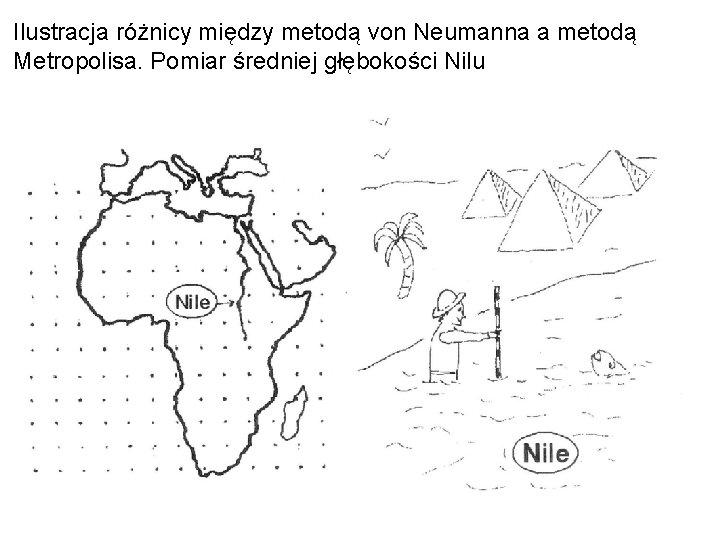
Ilustracja różnicy między metodą von Neumanna a metodą Metropolisa. Pomiar średniej głębokości Nilu

Metoda von Neumanna Obszar w którym chcemy policzyć wielkość uśrednioną pokrywamy siatką punktów i dla każdego z nich obliczamy gęstość prawdopodobieństwa oraz wielkość, którą chcemy uśrednić: Np. dla rozkładu Boltzmanna:

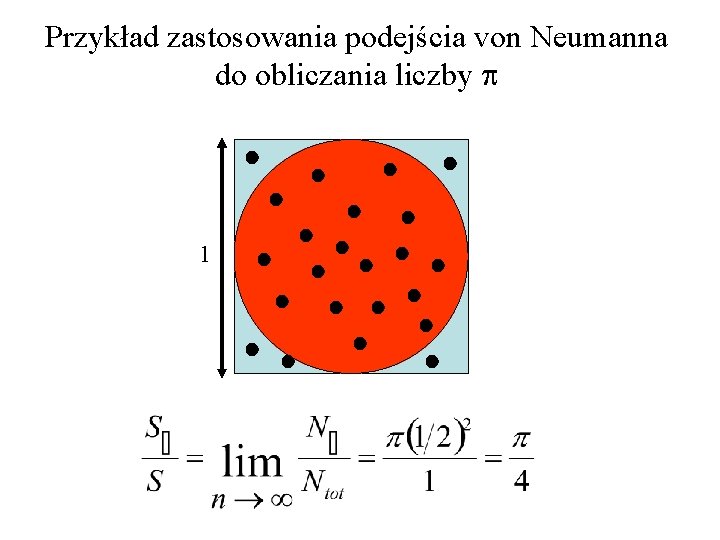
Przykład zastosowania podejścia von Neumanna do obliczania liczby p 1

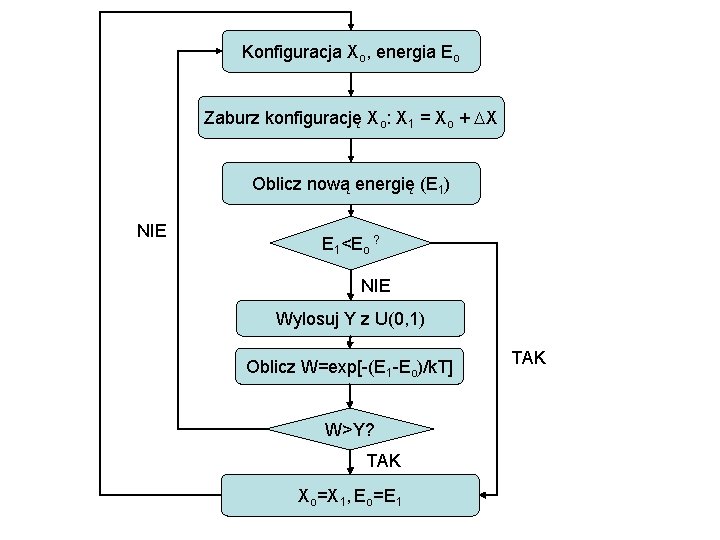
Metoda Metropolisa (łańcuchy Markowa) 1. Bierzemy startową konfigurację układu daną współrzędnymi (x 10, y 10, z 10, …, xn 0, yn 0, zn 0); tej konfiguracji odpowiada energia E 0. 2. Zaburzamy losowo wybraną współrzędną, np. xi 0 or Dxi (mała wartość). 3. Obliczamy energię nowej konfiguracji i oznaczamy ją jako E 1. 4. Jeżeli E 1<E 0 to nową konfigurację akceptujemy traktując jako nową konfigurację startową i przechodzimy do punktu 1; w przeciwnym przypadku przechodzimy do punktu 5. 5. Wykonujemy test Metropolisa: a) Generujemy liczbę losową y z przedziału (0, 1). b) Jeżeli exp[-(E 1 -E 0)/k. T]>y, (k jest stałą Boltzmanna) akceptujemy nową konfigurację, w przeciwnym przypadku przechodzimy do punktu 2 ze starą konfiguracją.

Konfiguracja Xo, energia Eo Zaburz konfigurację Xo: X 1 = Xo + DX Oblicz nową energię (E 1) NIE E 1<Eo ? NIE Wylosuj Y z U(0, 1) Oblicz W=exp[-(E 1 -Eo)/k. T] W>Y? TAK Xo=X 1, Eo=E 1 TAK

E 1 E 0 Akceptacja z prawdopodobieństwem exp[-(E 2 -E 1)/k. BT] Bezwzględna akceptacja E 1

Obliczanie średnich metodą Monte Carlo Średnia wielkości A Indeks i przebiega przez wszystkie kroki Monte Carlo, również te gdzie nowa konfiguracja nie została zaakceptowana. Tak więc jeżeli jakaś konfiguracja ma bardzo niską energię i nie chce przejść w alternatywną, będzie liczona wielokrotnie.

Reprezentacja przestrzeni w metodach Monte Carlo • Siatkowa (dyskretna). Centra oddziaływań mogą być tylko w węzłach sieci o określonej topologii. • Ciągła. Centra oddziaływań mogą przyjąć dowolne położenie w przestrzeni trójwymiarowej.

Zastosowania metody Metropolisa w chemii obliczeniowej • Wyznaczanie wielkości mechanicznych i termodynamicznych (gęstość, średnia energia, pojemność cieplna, przewodnictwo, współczynniki wirialne). • Symulacje przemian fazowych. • Symulacje właściwości polimerów. • Symulacje zwijania białek i innych biopolimerów. • Symulacje wiązania ligandów z receptorami oraz szacowanie energii swobodnej tego procesu (projektowanie leków). • Symulacje reakcji chemicznych.

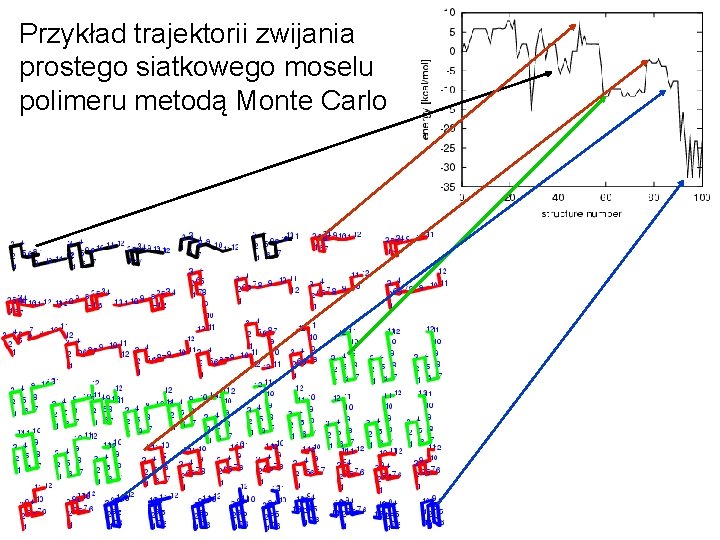
Przykład trajektorii zwijania Sample MC trajectory of a good folder; Model 1 a prostego siatkowego moselu polimeru metodą Monte Carlo

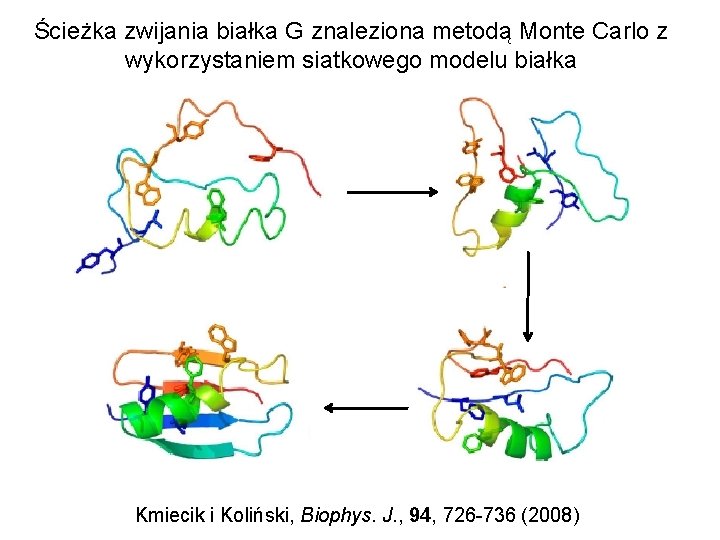
Ścieżka zwijania białka G znaleziona metodą Monte Carlo z wykorzystaniem siatkowego modelu białka Kmiecik i Koliński, Biophys. J. , 94, 726 -736 (2008)