WYKAD 4 Skojarzenia Skojarzenie w grafie G to

WYKŁAD 4. Skojarzenia • Skojarzenie w grafie G to niezależny zbiór krawędzi (rozłączne, bez wspólnych konców). • Skojarzenie M w G traktujemy jak podgraf G. • Wierzchołki w V(M) nazywamy M-nasyconymi. • α’(G) – moc największego skojarzenia w G (tutaj moc = liczba krawędzi).

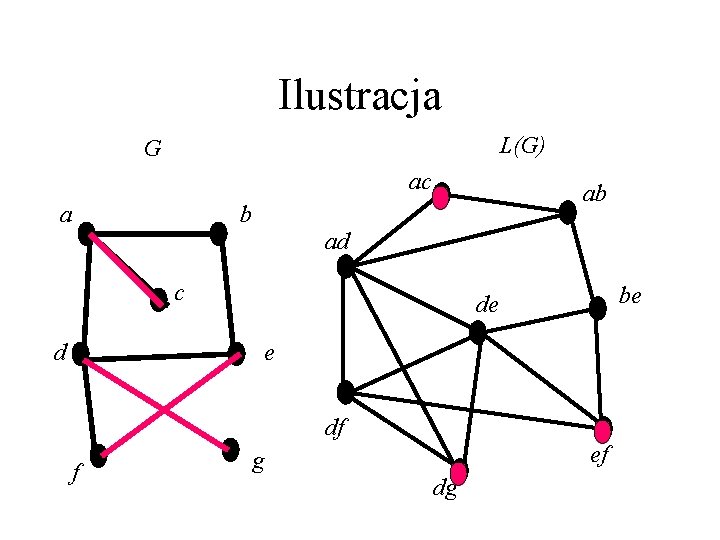
Graf krawędziowy • Graf krawędziowy danego grafu G to L(G)=(V’, E’), gdzie V’=E(G), a E’ składa się ze wszystkich par przecinających się krawędzi grafu G. • Zatem α’(G) =α(L(G)).

Ilustracja L(G) G ac a ab b ad c be de d e df f ef g dg

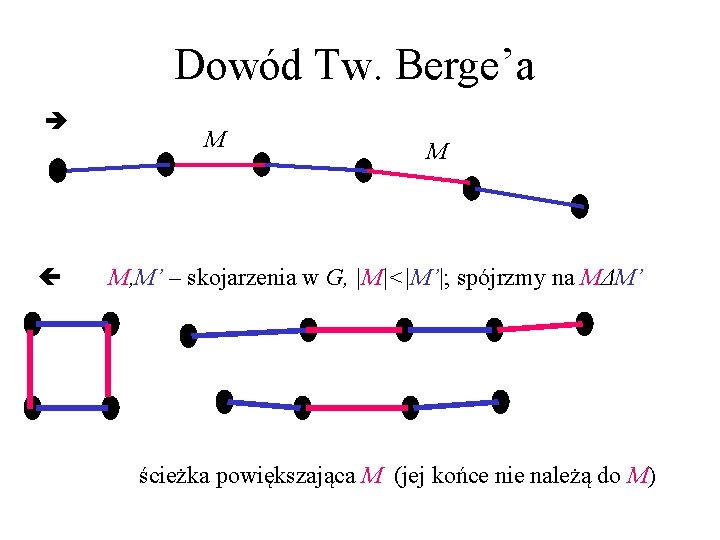
Ścieżki powiększające • Dane jest skojarzenie M w grafie G. • Ścieżka powiększająca M w G ma końce poza V(M), a co drugą krawędź w M. Twierdzenie (Berge, 1957) Skojarzenie M w grafie G ma moc |M|= α’(G) (tzn. jest największe) wgdy w G nie ma ścieżki powiększającej M.

Dowód Tw. Berge’a M M M, M’ – skojarzenia w G, |M|<|M’|; spójrzmy na MΔM’ ścieżka powiększająca M (jej końce nie należą do M)

Skojarzenia doskonałe • Skojarzenie M w grafie G nazywamy doskonałym, gdy |M|=|V(G)|/2. • Warunek konieczny: n=|V(G)| -- parzyste. • Składowa (spójności) – maksymalny podgraf spójny (każde dwie składowe grafu G są wierzchołkowo rozłączne).

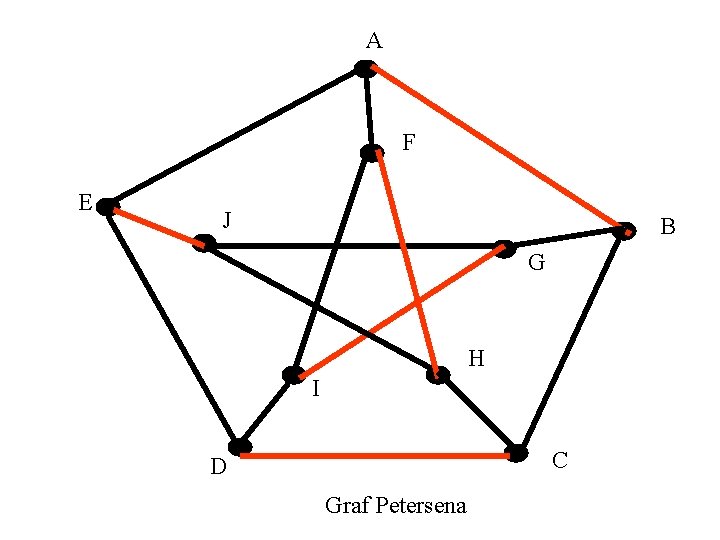
A F E J B G H I C D Graf Petersena

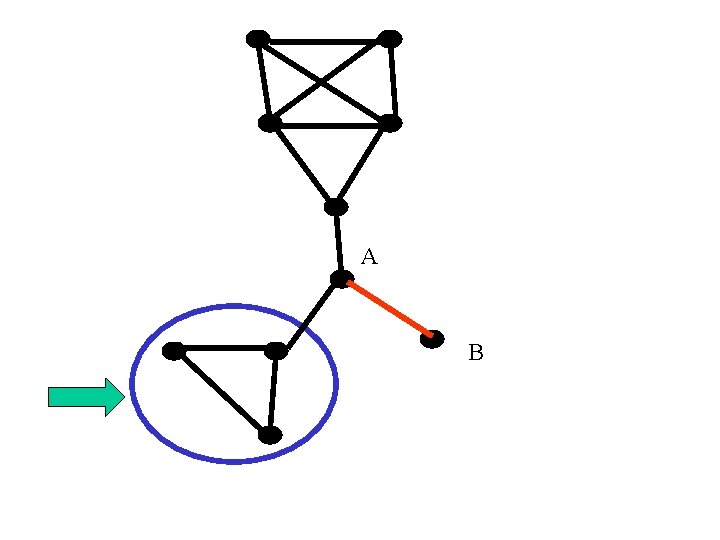
A B

A B

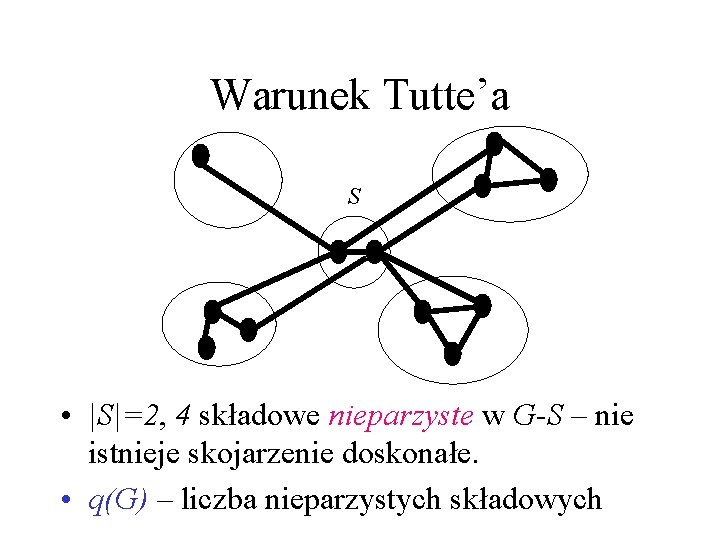
Warunek Tutte’a S • |S|=2, 4 składowe nieparzyste w G-S – nie istnieje skojarzenie doskonałe. • q(G) – liczba nieparzystych składowych

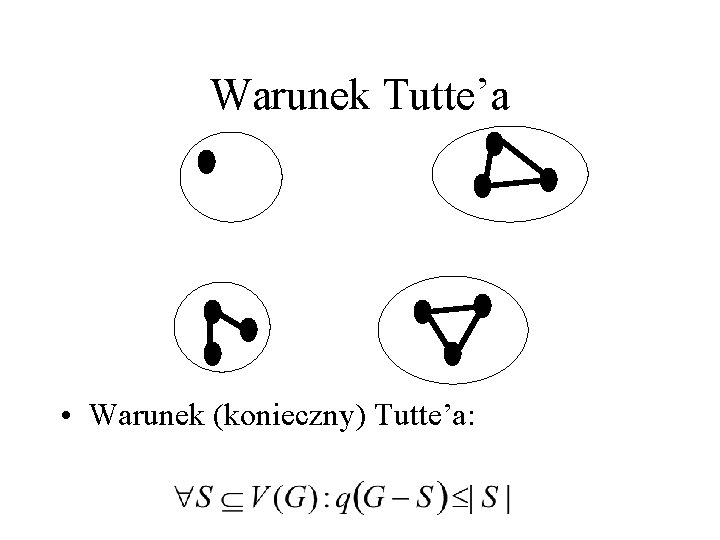
Warunek Tutte’a • Warunek (konieczny) Tutte’a:

Tw. Tutte’a Twierdzenie (Tutte, 1947) G ma skojarzenie doskonałe wgdy zachodzi warunek Tutte’a.

Dowód tw. Tutte’a (1) • Przypuśćmy, że istnieje graf, który spełnia warunek Tutte’a, ale nie ma skojarzenia doskonałego. • Niech G będzie takim grafem o największej liczbie krawędzi. • Dodanie dowolnej krawędzi do G nie narusza warunku Tutte’a (dlaczego? ), więc musi prowadzić do pojawienia się skojarzenia doskonałego.

Dowód tw. Tutte’a (2) • K – zbiór wierzchołków o stopniu n-1 • G’=G-K • Pokażemy, że w G’ wszystkie składowe są grafami pełnymi. • Wtedy, ponieważ q(G’) ≤ |K|, G będzie mieć skojarzenie doskonałe – sprzeczność.

Dowód tw. Tutte’a (3) • Przypuśćmy, że pewna składowa grafu G’ nie jest pełna, a więc istnieją w niej a, b, c takie, że ab i bc są krawędziami a ac nie. • Ponieważ b nie należy do K, to istnieje wierzchołek d taki, że bd nie jest krawędzią. • Niech M_1 będzie skojarzeniem doskonałym w G+ac, a M_2 w G+bd. • Oczywiście, ac jest w M_1, a bd w M_2.

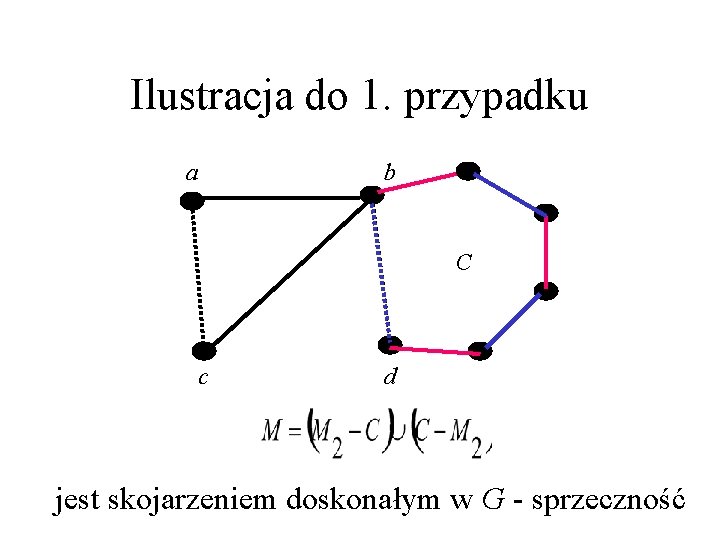
Dowód tw. Tutte’a (4) • Poprowadźmy w G maksymalną ścieżkę P wychodzącą z d i na przemian zawierającą krawędzie z M_1 i M_2. • P kończy się w b krawędzią z M_1 (przypadek 1. ) LUB w a lub c krawędzią z M_2 (przypadek 2. ), bo w przeciwnym razie można by P kontynuować. • W przypadku 1. , C =P+bd jest parzystym cyklem z co drugą krawędzią w M_2, a jedyną krawędzią w C poza G jest bd (która jest w M_2). • Zastępując w M_2 krawędzie z C, tymi z C-M_2, otrzymujemy skojarzenie doskonałe w G – sprzeczność.

Ilustracja do 1. przypadku a b C c d jest skojarzeniem doskonałym w G - sprzeczność

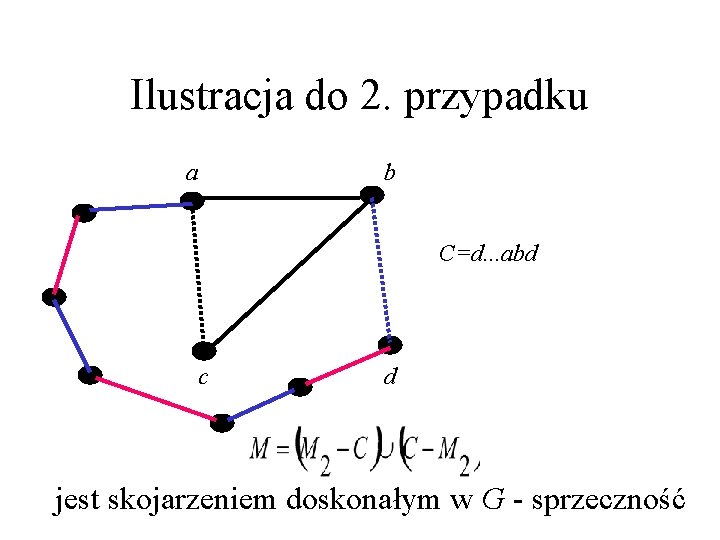
Dowód tw. Tutte’a (5) • W przypadku 2. , P kończy się krawędzią z M_2. Przyjmijmy, że jej ostatnim wierzchołkiem jest a. • C =P+ab+bd jest parzystym cyklem o tej samej własności co poprzednio. • Ponownie, zastępując w M_2 krawędzie z C, tymi z C-M_2, otrzymujemy skojarzenie doskonałe w G – sprzeczność.

Ilustracja do 2. przypadku a b C=d. . . abd c d jest skojarzeniem doskonałym w G - sprzeczność

Wniosek – Tw. Petersena • Most (krawędź cięcia) to taka krawędź e, że G-e ma więcej składowych niż G. Np. Petersen (1891) Każdy 3 -regularny graf bez mostów ma skojarzenie doskonałe. (dowód na ćwiczeniach)

Pokrycia wierzchołkowe Podzbiór U zbioru V(G) nazywamy pokryciem wierzchołkowym (krawędzi), jeśli każda krawędź grafu G ma przynajmniej jeden koniec w U. Moc najmniejszego pokrycia - β(G). Trywialnie,

Skojarzenia w grafach 2 dzielnych – tw. Königa Twierdzenie (König , 1931) Dla grafów dwudzielnych α’(G)= β(G)

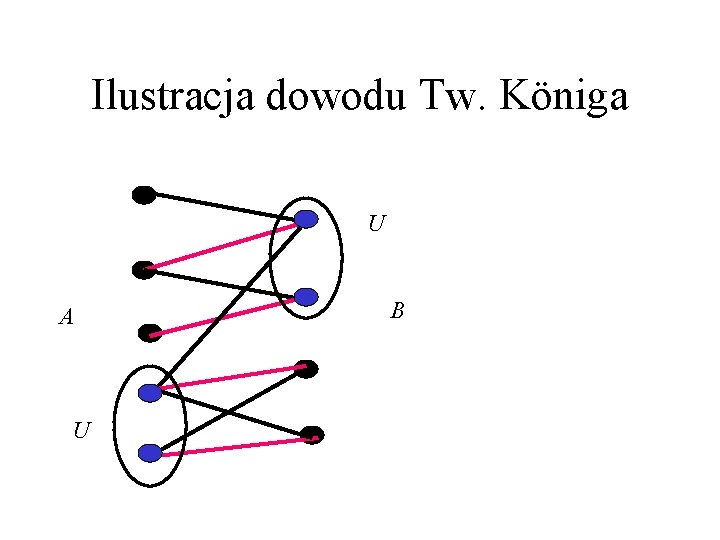
Dowód tw. Königa (1) • Niech M będzie największym skojarzeniem w grafie 2 -dzielnym G o dwupodziale (A, B). • Wystarczy pokazać, że istnieje pokrycie U mocy |M|. • Ścieżka M-naprzemienna ma jeden koniec w AV(M) i co drugą krawędź w M. • Konstrukcja zbioru U: do U zaliczamy po 1 końcu każdej krawędzi M; wybieramy koniec w B, gdy kończy się w nim jakaś M-naprzemienna ścieżka, a koniec w A – w przeciwnym razie.

Ilustracja dowodu Tw. Königa U A U B

Dowód tw. Königa (2) • • Niech ab będzie krawędzią (a z A, a b z B). Pokażemy, że a lub b jest w U. Tak jest, gdy ab jest krawędzią skojarzenia M. W przeciwnym razie M zawiera krawędź a’b lub ab’ (bo M jest maksymalne).

Dowód tw. Königa (3) • W pierwszym przypadku (gdy nie zachodzi drugi), krawędź ab jest ścieżką Mnaprzemienną, więc b jest w U. • W drugim przypadku, jeśli a nie jest w U, to b’ jest, tzn. b’ jest końcem M-naprzemiennej ścieżki, która omija a i b. • Przedłużając te ścieżkę o krawędzie b’a i ab, otrzymujemy też M-naprzemienną ścieżkę, a że nie jest to ścieżka M-powiększająca (M jest największe!), to b należy do M, a więc także do U. �