www muratguner net HER GEN MATEMATK RENEBLR MURAT

www. muratguner. net HER GENÇ MATEMATİK ÖĞRENEBİLİR MURAT GÜNER 2012
www. muratguner. net İÇİNDEKİLER TANIM 3 GEOMETRİK DİZİNİN ÖZELLİKLERİ 7 SONSUZ GEOMETRİK DİZİNİN TOPLAMI 38 KAYNAKÇA 73

www. muratguner. net TANIM Ardışık iki terimi arasındaki oranı sabit olan dizilere geometrik dizi denir. 3 x 3 x 3 x Örneğin: (an ) = ( 3, 9, 27, …, 3 n, …) = ( 3 n ) 25 x 25 x (bn ) = 1 1 (cn ) = ( 6, 6, …, 6, …) TANIM n N+ ve r R olmak üzere eşitliğini sağlayan ( an) dizisi, bir geometrik dizidir. Bu r sayısına dizinin ortak çarpanı (ortak oranı) denir. Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Aşağıdaki dizilerin geometrik dizi olduğunu gösteriniz. A) (an ) = ( πn ) B) (bn ) = ((– 1)n) C) ( cn ) = ( ) D) (dn ) = (2) ÇÖZÜM n N+++ için n N+ için rr == 1(sabit) olduğundan (( da(nnb))ndizisi geometrik dizidir. – 1 (sabit) olduğundan ) dizisi geometrik dizidir. π(sabit) olduğundan dizisi geometrik dizidir. r = 1/2(sabit) olduğundan ( cn ) dizisi geometrik dizidir. Sıfır dizisi hariç bütün sabit diziler geometrik dizidir ve ortak çarpanı 1 dir. Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK ( an ) bir geometrik dizidir. a 100 oranı kaçtır? a 99 ÇÖZÜM Ana Sayfaya Geri Dön olduğuna göre

www. muratguner. net ÖRNEK 3 a + 2 b – 4, 2 b + 4 a, a 3 – 2 b terimleri hem aritmetik hem de geometrik dizi oluşturduğuna göre, a – b farkı kaçtır? ÇÖZÜM Bir dizinin hem aritmetik hem de geometrik bir dizi olması için dizinin terimleri eşit olmalıdır. Yani, sabit dizi olmalıdır. ( a 1= a 2 = a 3 = …= an = …) 3 a + 2 b – 4 = 2 b + 4 a a=– 4 a 3 – 2 b = 2 b + 4 a b = – 12 a – b= 8 Ana Sayfaya Geri Dön

www. muratguner. net GEOMETRİK DİZİNİN ÖZELLİKLERİ 1 İlk terimi a 1 ve ortak çarpanı r olan geometrik dizinin genel terimi an = a 1. r n– 1 dir. İSPAT a 1 = a 1 a 2 = a 1. r a 3 = a 2. r = a 1. r 2 a 4 = a 3. r = a 1. r 2. r = a 1. r 3 … a 5 = a 4. r = a 1. r 3. r = a 1. r 4 an = a 1. r (n – 1) ( Geometrik Dizinin Genel Terimi) Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK ( an ) geometrik dizidir. a 1 = 3 ve ortak çarpan 4 olduğuna göre, a 2+a 4 kaçtır? ÇÖZÜM –– 21 ÇÖZÜM a 2 = a 1. r a 2 =3 3. 4 =12 3 a 2 + a 4= a 1. r + a 1 r = a 1( r +r ) = 3. ( 4 + 43 ) = 3. 68 = 204 a 4 = a 1. r 3 a 2 = 3. 43 =192 + a 2+a 4 = 204 Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK İkinci terimi 27, ortak çarpanı 1/3 olan bir geometrik dizinin kaçıncı terimi 1/27 dir? ÇÖZÜM a 2 = 27 ve r = 1/3 ise ax =1/27 Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Bir bakteri çeşidinin sayısı, uygun bir ortamda her 10 dakikada 2 katına çıkmaktadır. Başlangıçta ortamda 60 tane bakteri olduğuna göre, bir günün sonunda ortamda kaç tane bakteri olur? ÇÖZÜM a 1 = 60 a 2 = 60. 2 a 3 = 60. 2. 2 = 60. 22 … a 4 = 60. 2. 2. 2 = 60. 23 a 144 = 60. 2143 Ana Sayfaya Geri Dön ( Bir saat 6 x 10 dakika olduğundan bir günde 24 x 6 =144 defa çoğalma işlemi olacaktır. 144. çoğalmada ki bakteri sayısı)

www. muratguner. net 2 İlk terimi a 1, ortak çarpanı r olan aritmetik dizinin herhangi bir terimi ak = ap. r( k – p ) dir. ( k > p) İSPAT ak = a 1. r( k – 1 ) ap = a 1. r( p – 1 ) ak ap = r( k – p ) ak = ap. r( k – p ) = ak ap Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK ( an ) monoton bir geometrik dizidir. a 3 = 8 ve a 7 = 128 olduğuna göre, a 10 kaçtır? ÇÖZÜM r( k – p ) = ak ap ( an ) monoton bir geometrik dizi olduğundan r = 2 dir. ak = ap. r( k – p ) Ana Sayfaya Geri Dön a 10 = a 7. r( 10 – 7 ) veya a 10 = a 3. r( 10 – 3 ) a 10 = 128. 23 a 10 = 8. 27 a 10 = 1024

www. muratguner. net ÖRNEK ( an ) bir geometrik dizidir. a 3 = 4 ve a 6 = 32 olduğuna göre, ( an ) dizisinin genel terimini bulunuz. ÇÖZÜM r( k – p ) = ak ap ak = ap. r( k – p ) an = a 6. r( n – 6 ) an = 32. 2( n – 6 ) an = 2 n – 1 Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Bir konveks dörtgenin iç açıları bir geometrik dizinin ardışık terimleridir. Bu açılardan birincisi, üçüncünün 4 katıdır. Buna göre, bu açılardan en büyüğü kaç derecedir? ÇÖZÜM a 1 a 2 a 3 a 4 8 x 4 x 2 x x 8 x + 4 x + 2 x + x = 360º 15 x = 360º x = 24º Ana Sayfaya Geri Dön 8 x = 192º ( en büyük açı)

www. muratguner. net ÖRNEK 12 ile 96 sayıları arasına geometrik dizi oluşturacak şekilde beş terim yerleştiriliyor. Buna göre dizinin 13. terimi kaçtır? ÇÖZÜM 12 a 1 - - a 2 r( k – p ) = a 3 ak ap ak = ap. r( k – p ) Ana Sayfaya Geri Dön - a 4 - - a 5 a 6 96 a 7 a 13 = a 7. r( 13 – 7 ) = 96. r 6 = 96. 8 =768
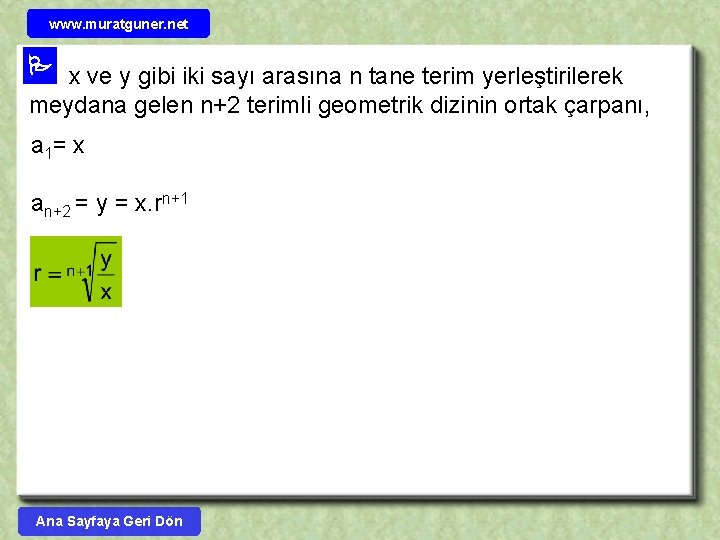
www. muratguner. net x ve y gibi iki sayı arasına n tane terim yerleştirilerek meydana gelen n+2 terimli geometrik dizinin ortak çarpanı, a 1= x an+2 = y = x. rn+1 Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Bir geometrik dizinin ardışık beş terimi olduğuna göre, ifadesinin değerini hesaplayınız. ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net 3 Sonlu bir geometrik dizide, sondan ve baştan eşit uzaklıkta bulunan terimlerin çarpımı birbirine eşittir. Yani, a 1. an = a 2. an – 1 = …= an. a 1 İSPAT a 1, a 2 , a 3, …an – 2 , an – 1 , an bir geometrik dizi olsun. a 1. an = a 1. rn – 1 = a 12. rn – 1 a 2. an – 1 = ( a 1. r )(a 1. rn – 2 ) = a 12. rn – 1 … a 3. an – 2 = ( a 1. r 2 )(a 1. rn – 3 ) = a 12. rn – 1 Bu şekilde devam edilirse a 1. an = a 2. an – 1 = …= an. a 1 elde edilir. Ana Sayfaya Geri Dön İndisler toplamının eşit olduğuna dikkat ediniz.

www. muratguner. net Bir geometrik dizide indisler toplamı eşit olan her n terimin çarpımı da eşittir. Yani, p, r, s, t N+ olmak üzere, p + r = s + t ise ap. ar = as. at Örneğin; a 5. a 12 = a 3. a 14 = a 8. a 9 = a 10. a 7 =… 5+12=17 3+14=17 8+9=17 10+7=17 a 5. a 12. a 3 = a 8. a 9. a 3 =… ( 5+12+3 = 8+9+3=20 ) UYARI Bir geometrik dizide indisler toplamı aynı olmasına rağmen indisleri toplanan terimlerin sayısı eşit değilse yukarıdaki yöntemi kullanamayız. Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Bir geometrik dizide, a 3. a 6 = 1 ise dizinin baştan itibaren kaç teriminin çarpımı 1 dir? ÇÖZÜM a 1 a 2 a 3 a 4 a 5 a 6 a 4. a 5 = 1 a 3. a 6 = 1 a 2. a 7 = 1 a 1. a 8 = 1 a 1. a 2. a 3. a 4. a 5. a 6. a 7. a 8 = 1. 1 =1 Ana Sayfaya Geri Dön a 7 a 8. . .
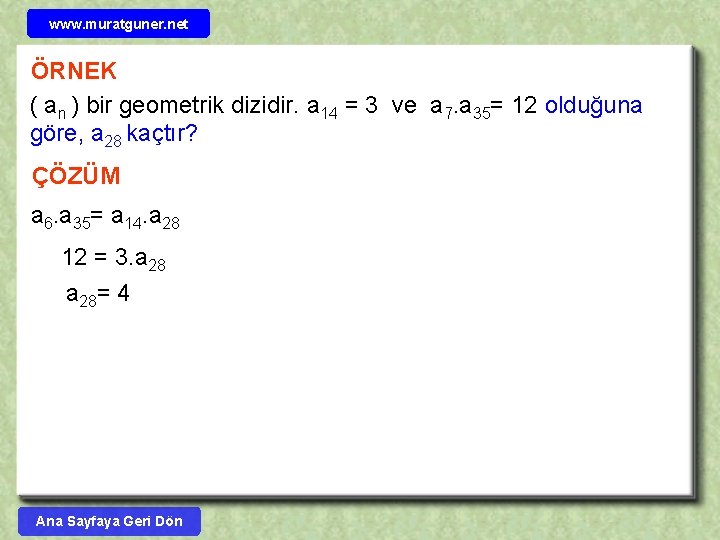
www. muratguner. net ÖRNEK ( an ) bir geometrik dizidir. a 14 = 3 ve a 7. a 35= 12 olduğuna göre, a 28 kaçtır? ÇÖZÜM a 6. a 35= a 14. a 28 12 = 3. a 28= 4 Ana Sayfaya Geri Dön
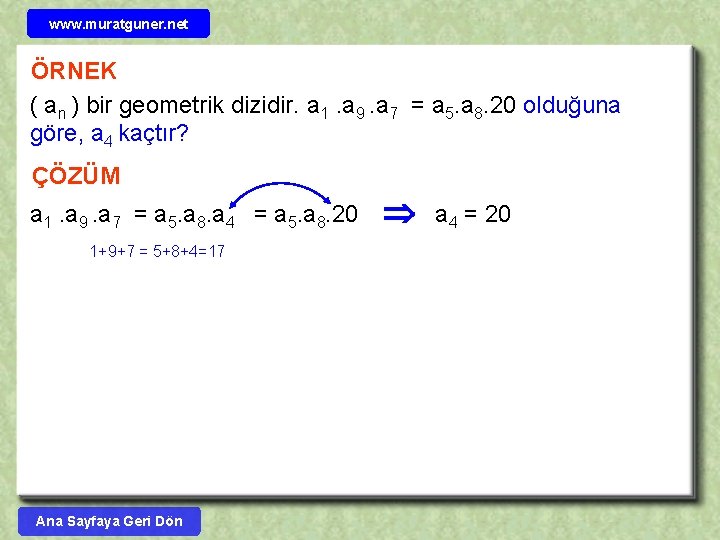
www. muratguner. net ÖRNEK ( an ) bir geometrik dizidir. a 1. a 9. a 7 = a 5. a 8. 20 olduğuna göre, a 4 kaçtır? ÇÖZÜM a 1. a 9. a 7 = a 5. a 8. a 4 = a 5. a 8. 20 1+9+7 = 5+8+4=17 Ana Sayfaya Geri Dön a 4 = 20
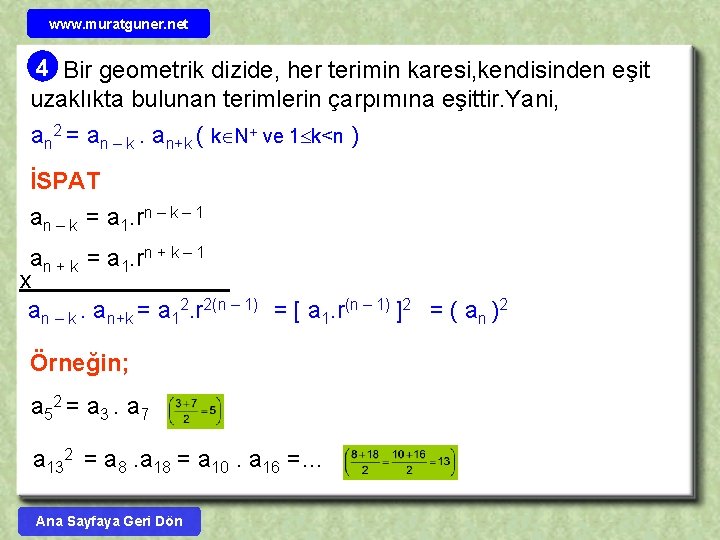
www. muratguner. net 4 Bir geometrik dizide, her terimin karesi, kendisinden eşit uzaklıkta bulunan terimlerin çarpımına eşittir. Yani, an 2 = an – k. an+k ( k N+ ve 1 k<n ) İSPAT an – k = a 1. rn – k – 1 an + k = a 1. rn + k – 1 x an – k. an+k = a 12. r 2(n – 1) = [ a 1. r(n – 1) ]2 = ( an )2 Örneğin; a 52 = a 3. a 7 a 132 = a 8. a 18 = a 10. a 16 =… Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK ( an ) bir geometrik dizidir. kaçtır? ÇÖZÜM an 2 = an – k. an+k ( k N+ ve 1 k<n ) Ana Sayfaya Geri Dön olduğuna göre, n

www. muratguner. net ÖYS -1992 ÖRNEK Bir geometrik dizinin ardışık terimi sırasıyla (x – 2), (x+1), (x+5) olduğuna göre, x kaçtır? ÇÖZÜM an 2 = an – k. an+k ( k N+ ve 1 k<n ) (x +1)2 = (x – 2)( x + 5) x 2 + 2 x + 1 = x 2 + 3 x – 10 x = 11 Ana Sayfaya Geri Dön

www. muratguner. net ÖYS -1998 ÖRNEK Bir geometrik dizinin ilk üç terimi sırasıyla (a – 3), (2 a – 3 ), ( 4 a + 3) olduğuna göre, bu dizinin 5. terimi kaçtır? ÇÖZÜM an 2 = an – k. an+k ( k N+ ve 1 k<n ) (2 a – 3)2 = (a – 3)( 4 a + 3 ) 4 a 2 – 12 a + 9 = 4 a 2 – 9 a – 9 3 a = 18 a=6 (a – 3), (2 a – 3 ), ( 4 a + 3) a 1=3 a 2= 9 a 3=27 Ana Sayfaya Geri Dön a 5= a 1. r 4 = 3. 34 = 243

www. muratguner. net ÖRNEK 7 terimli bir geometrik dizide orta terim 3 ise terimlerin çarpımı kaçtır? ÇÖZÜM a 1 a 2 a 3 3 a 4 a 5 a 42 = a 3. a 5 = 9 a 42 = a 2. a 6 = 9 a 42 = a 1. a 7 = 9 a 1. a 2. a 3. a 4. a 5. a 6. a 7 = 3. 9. 9. 9 =37 Ana Sayfaya Geri Dön a 6 a 7
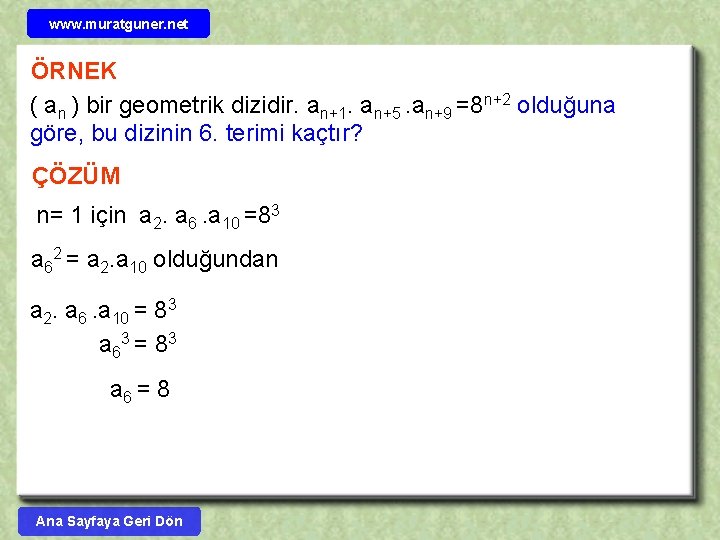
www. muratguner. net ÖRNEK ( an ) bir geometrik dizidir. an+1. an+5. an+9 =8 n+2 olduğuna göre, bu dizinin 6. terimi kaçtır? ÇÖZÜM n= 1 için a 2. a 6. a 10 =83 a 62 = a 2. a 10 olduğundan a 2. a 6. a 10 = 83 a 63 = 8 3 a 6 = 8 Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK mx 3 + (5 m+2)x 2 + 14 x + 8 m = 0 denkleminin kökleri, bir geometrik dizinin ardışık üç terimi olması için m ne olmalıdır? ÇÖZÜM mx 3 + (5 m+2)x 2 + 14 x + 8 m = 0 denkleminin kökleri: x 1 , x 2 ve x 3 olsun. x 22 =x 1. x 3 x 1. x 2. x 3 =– d/a x 1. x 2. x 3 = – 8 x 2 = – 2 Ana Sayfaya Geri Dön x 2 =– 2 kök olduğundan denklemi sağlar. m(– 2)3 + (5 m+2)(– 2)2 + 14. (– 2) + 8 m = 0 20 m – 20 = 0 m =1
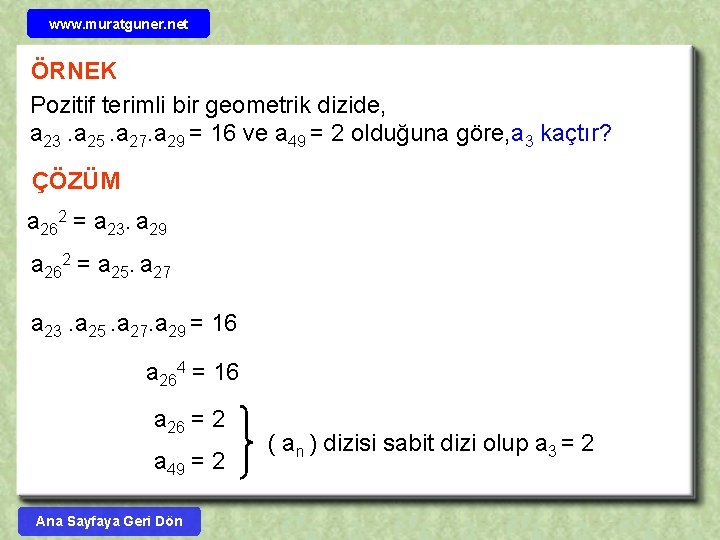
www. muratguner. net ÖRNEK Pozitif terimli bir geometrik dizide, a 23. a 25. a 27. a 29 = 16 ve a 49 = 2 olduğuna göre, a 3 kaçtır? ÇÖZÜM a 262 = a 23. a 29 a 262 = a 25. a 27 a 23. a 25. a 27. a 29 = 16 a 264 = 16 a 26 = 2 a 49 = 2 Ana Sayfaya Geri Dön ( an ) dizisi sabit dizi olup a 3 = 2
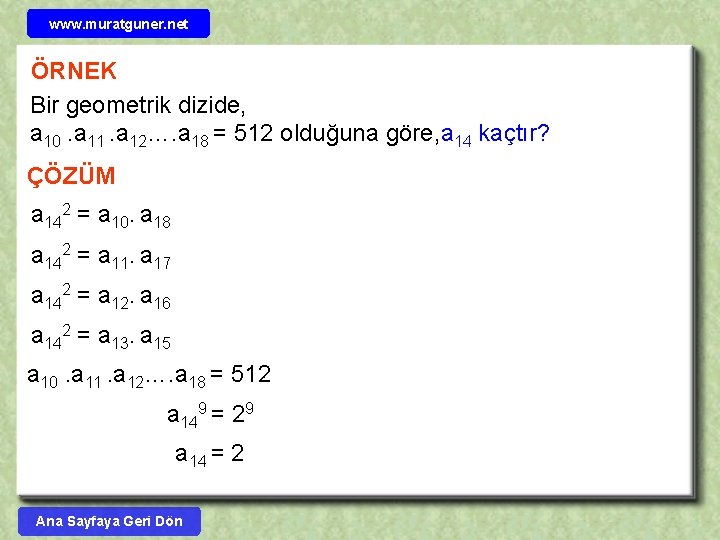
www. muratguner. net ÖRNEK Bir geometrik dizide, a 10. a 11. a 12…. a 18 = 512 olduğuna göre, a 14 kaçtır? ÇÖZÜM a 142 = a 10. a 18 a 142 = a 11. a 17 a 142 = a 12. a 16 a 142 = a 13. a 15 a 10. a 11. a 12…. a 18 = 512 a 149 = 29 a 14 = 2 Ana Sayfaya Geri Dön

www. muratguner. net 5 İlk terimi a 1, ortak çarpı r olan ( an) =( a 1. rn – 1 ) geometrik dizisinin ilk n terim toplamı, 1 - rn Sn = a 1. 1 -r İSPAT Sn= a 1+ a 2 + a 3 + a 4+…. + an – 1 + an Sn= a 1+ (a 1. r) + (a 1 r 2 ) + (a 1. r 3)+…. + (a 1 rn– 1) r. Sn= r. a 1+ a 1. r 2 + a 1 r 3 + a 1. r 4 +…. a 1 rn– 1 + a 1 rn – Sn – r. Sn = a 1 – a 1 rn Sn (1 – r ) = a 1(1 – rn ) 1 - rn Sn = a 1. 1 -r Ana Sayfaya Geri Dön
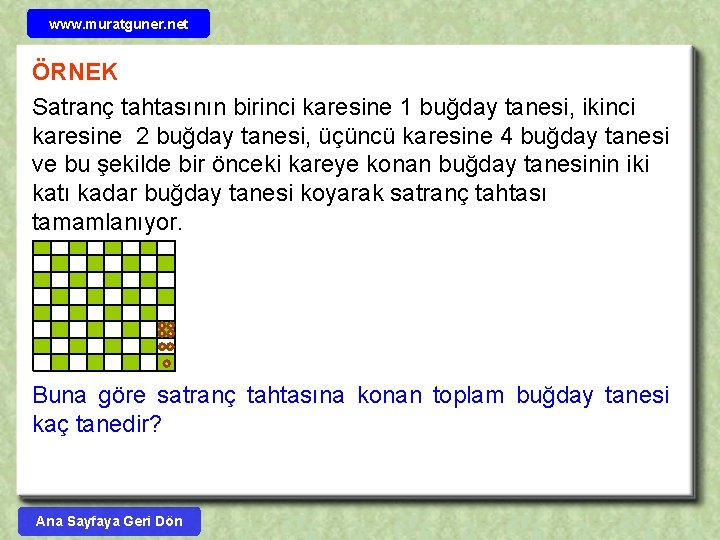
www. muratguner. net ÖRNEK Satranç tahtasının birinci karesine 1 buğday tanesi, ikinci karesine 2 buğday tanesi, üçüncü karesine 4 buğday tanesi ve bu şekilde bir önceki kareye konan buğday tanesinin iki katı kadar buğday tanesi koyarak satranç tahtası tamamlanıyor. Buna göre satranç tahtasına konan toplam buğday tanesi kaç tanedir? Ana Sayfaya Geri Dön

www. muratguner. net ÇÖZÜM Önce buğday sayısını hesaplayalım. tane buğday tanesi var. 25000 buğday tanesi 1 kğ dır. 25. 1012 buğday tanesi 1 milyon tondur. 264 – 1 tanesi 737870 milyon tondur. Dünyanın bir yıllık buğday üretimi ( 2010 yılına göre) ortalama 600 milyon tondur. Bu ürünün tamamı bugünden itibaren ödenmeye başlansa yaklaşık 1230 yıl sonra tamamlanmış olur. Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Bir geometrik dizinin 1. terimi ortak çarpanının 2 katıdır. S 15 – S 14 = 231 olduğuna göre, bu dizinin ilk üç teriminin toplamı kaçtır? ÇÖZÜM a 1= 2 r S 15 – S 14 = a 15 = 231 = 2 r. r 14 30 = r 15 2 14 a = a. r 15 1 Ana Sayfaya Geri Dön r=4
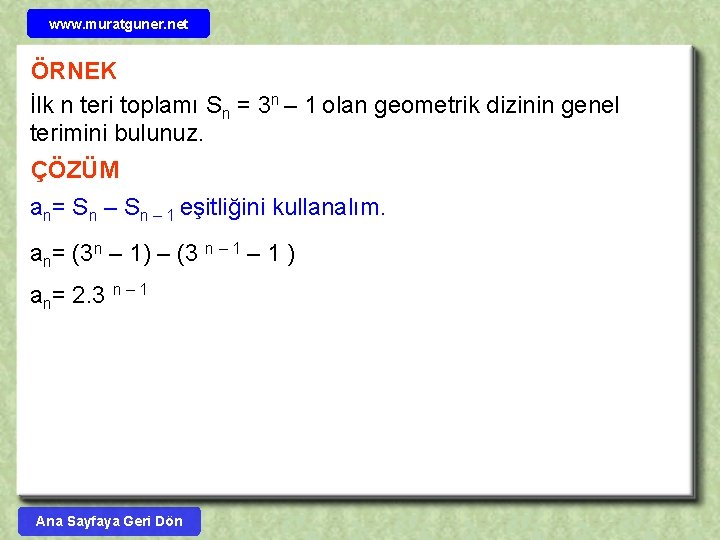
www. muratguner. net ÖRNEK İlk n teri toplamı Sn = 3 n – 1 olan geometrik dizinin genel terimini bulunuz. ÇÖZÜM an= Sn – 1 eşitliğini kullanalım. an= (3 n – 1) – (3 n – 1 ) an= 2. 3 n – 1 Ana Sayfaya Geri Dön

www. muratguner. net ÖYS -1993 ÖRNEK Bir geometrik dizinin ilk altı teriminin toplamının ilk üç teriminin toplamına oranı dir. Bu dizinin ortak çarpanı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK toplamının 5 ile bölümünden kalan kaçır? ÇÖZÜM LYS 2010
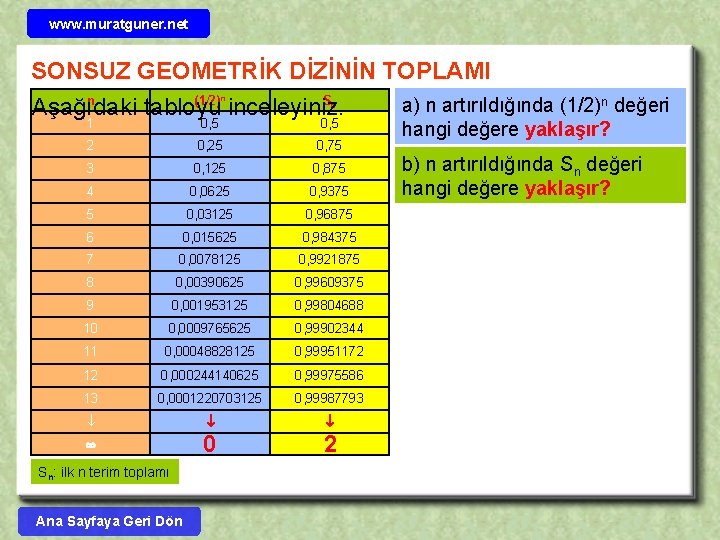
www. muratguner. net SONSUZ GEOMETRİK DİZİNİN TOPLAMI n (1/2) S a) n artırıldığında (1/2)n değeri Aşağıdaki tabloyu inceleyiniz. n n 1 0, 5 2 0, 25 0, 75 3 0, 125 0, 875 4 0, 0625 0, 9375 5 0, 03125 0, 96875 6 0, 015625 0, 984375 7 0, 0078125 0, 9921875 8 0, 00390625 0, 99609375 9 0, 001953125 0, 99804688 10 0, 0009765625 0, 99902344 11 0, 00048828125 0, 99951172 12 0, 000244140625 0, 99975586 13 0, 0001220703125 0, 99987793 0 2 Sn: ilk n terim toplamı Ana Sayfaya Geri Dön hangi değere yaklaşır? b) n artırıldığında Sn değeri hangi değere yaklaşır?

www. muratguner. net TANIM ( an ) = ( a 1. rn – 1 ) geometrik dizisi için ifadesine sonsuz geometrik dizinin toplamı denir. ( an ) = ( a 1. rn – 1 ) geometrik dizisinin ilk n terim toplamı; Bu toplamı, n sayısını sonsuza yaklaştırarak inceleyelim. Ana Sayfaya Geri Dön

www. muratguner. net I r I < 1 ise n sonsuza yaklaştığında rn değeri sıfıra yaklaşır. bu durumda, n için rn 0 ve Sn değeri Ana Sayfaya Geri Dön ye yaklaşır. Yani;

www. muratguner. net I r I > 1 ise n sonsuza yaklaştığında I r In değeri sınırsız olarak artar. Bu durumda n için Sn ± olur. Buna göre S değeri bir gerçek sayıya yaklaşmaz. r = 1 ise ( an ) = ( a 1, …) sabit dizisi elde edilir. Sn= n. a 1 olur. Bu durumda n için Sn ± olur. Buna göre S değeri bir gerçek sayıya yaklaşmaz. r = -1 ise ( an ) = ( a 1, -a 1, …) dizisi elde edilir. Sn = a 1 , n tek ise 0, n çift ise Bu durumda da n için S değeri belirlenemez Ana Sayfaya Geri Dön
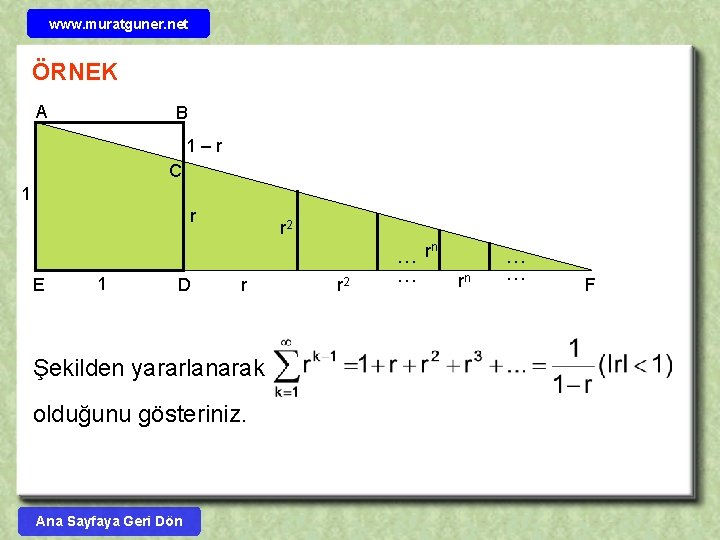
www. muratguner. net ÖRNEK A B 1–r C 1 r E 1 D r 2 r Şekilden yararlanarak olduğunu gösteriniz. Ana Sayfaya Geri Dön r 2 … rn … … F

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK x 2 < x olmak üzere x + x 2 + x 3 +…+ xn – 1 + …= 4 olduğuna göre, x kaçtır? ÇÖZÜM x 2 < x ise 0 < x < 1 x + x 2 + x 3 +…+ xn – 1 + …= 4 x. (1+ x 2 + x 3 +…+ xn – 2 + …)= 4 4 – 4 x = x 5 x = 4/5 Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK 0, 7=0, 7777… devirli ondalık açılımını, sonsuz geometrik dizinin toplamı biçiminde gösterip rasyonel sayı olarak yazalım. ÇÖZÜM 0, 7=0, 7777…= 0, 07 + … 0, 007 0, 7=0, 7777… Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK x [ 1, ) ve serisinin değeri olduğuna göre, x kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön x=3

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK 1 – 0, 1+ ( 0, 1)2 – (0, 1)3 + … geometrik serisinin toplamı kaçtır? ÇÖZÜM 1– 0, 1 + (0, 1)2 – (0, 1)3+…= 1 + (– 0, 1)2 + ( – 0, 1)3 + … Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK serisinin toplamı kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK olduğuna göre, k kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön
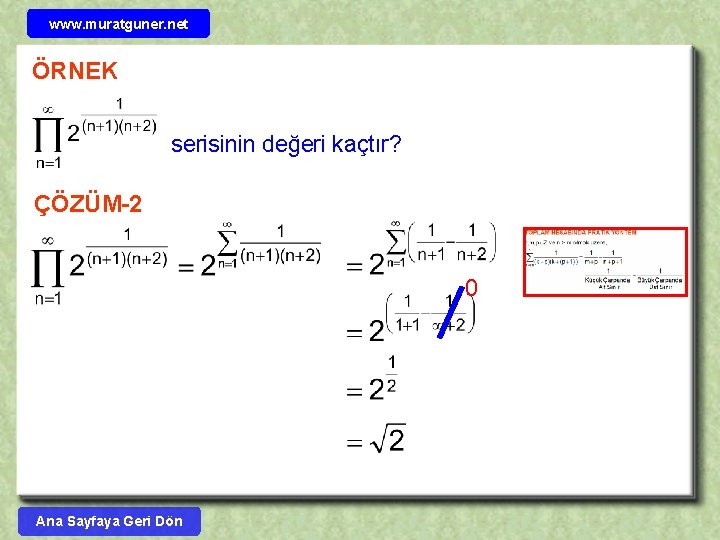
www. muratguner. net ÖRNEK serisinin değeri kaçtır? ÇÖZÜM-1 ÇÖZÜM-2 0 Ana Sayfaya Geri Dön

www. muratguner. net I r I < 1 olmak üzere İSPAT r 2 = t olsun. I r I < 1 ise r 2 < 1 olur. İSPAT Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK I r I < 1 olmak üzere olduğuna göre, ÇÖZÜM Ana Sayfaya Geri Dön serisinin toplamı kaçtır?

www. muratguner. net ÖRNEK Ortak çarpanı r olan bir sonsuz geometrik dizinin toplamı 4 ve bu dizinin terimlerinin kareleri toplamı 48/5 olduğuna göre, r kaçtır? ÇÖZÜM sonsuz geometrik dizisinin değeri 4 olduğuna göre Ir. I<1 dir. a 1 , a 2, a 3 , a 4, … a 1, a 1 r 2, a 1 r 3 , … (a 1)2 + ( a 1 r)2 + (a 1 r 2)2 +…=48/5 (a 1)2 ( 1 + r 2 + r 4 +…) = 48/5 Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK toplamının sonucu kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK 1+2 r + 3 r 2 + 4 r 3 +…+n. rn – 1 …= ÇÖZÜM 1+ 2 r + 3 r 2 + 4 r 3 + … = T r + 2 r 2 + 3 r 3 + 4 r 4 + …= T. r – 1+ r 2 + r 3 + … = T. ( 1 – r ) Ana Sayfaya Geri Dön (Ir. I<1) olduğunu gösteriniz.

www. muratguner. net ÖRNEK serisinin değeri kaçtır? ÇÖZÜM Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Bir top 24 metre yükseklikten bırakılıyor. Top yere her çarptığında bir önceki düştüğü yüksekliğin 1/4’ü kadar yükseliyor. Buna göre, topun duruncaya kadar dikey olarak izlemiş olduğu toplam yol kaç metredir? ÇÖZÜM – 1 24 1 2 Ana Sayfaya Geri Dön 3 4 … …

www. muratguner. net 24 1 2 3 4 Topun izlemiş olduğu toplam yol : Ana Sayfaya Geri Dön … …

www. muratguner. net a < b olmak üzere, h kadar yükseklikten bırakılan top yere her çarptığında bir önceki düştüğü yüksekliğin a/b si kadar yükselsin. Topun duruncaya kadar dikey olarak izlemiş olduğu toplam yol: Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Bir top 24 metre yükseklikten bırakılıyor. Top yere her çarptığında bir önceki düştüğü yüksekliğin 1/4’ü kadar yükseliyor. Buna göre, topun duruncaya kadar dikey olarak izlemiş olduğu toplam yol kaç metredir? ÇÖZÜM – 2 Topun izlemiş olduğu toplam yol : Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK Dikildiğinde 20 cm olan bir fidanın boyu 1 yıl sonra 1 m oluyor. Fidan bundan sonra her yıl bir önceki yıldaki uzama miktarının 1/9 u kadar uzuyor. Buna göre fidanın boyu en fazla kaç cm olabilir? ÇÖZÜM Fidanın Boyu : = = Ana Sayfaya Geri Dön =

www. muratguner. net ÖRNEK Şekildeki gibi yarıçapı 20 cm olan çemberin içine yarıçapının 2/3 katı olan iç içe sonsuz çoklukta çemberler çiziliyor. Bütün bu çemberlerin çevreleri toplamı kaç π dir? ÇÖZÜM Toplam çevre: 2π. 20 + 2π. 20. = 2π. 20 + 2π. 20. +… = 2π. 20. = 120π Ana Sayfaya Geri Dön

www. muratguner. net ÖRNEK ABC üçgeni eşkenardır. Şekildeki üçgenlerin her biri bir öncekinin kenarlarının orta noktaları birleştirilerek elde edilmiştir. A(ABC) =12 cm 2 ise bütün üçgenlerin alanları toplamı kaçtır? B A ÇÖZÜM ABC nin bir kenarı a br olsun. Kırmızı üçgenin bir kenarı a/2 br Alan = üçgenin bir kenarı ise a/4 br olur ve bu şekilde olur. Yeşil sonsuza kadar devam edilirse; Ana Sayfaya Geri Dön C

www. muratguner. net ÖRNEK Yarıçapı 8 cm olan en dıştaki çemberin içine kare ve çemberler çizilerek devam etmektedir. Kareler dıştaki çember için krişler dörtgeni, içteki çember için teğetler dörtgenindir. Buna göre taralı alanların toplamı kaç cm 2 dir? ÇÖZÜM 2 = 64π 1. Dairenin alanı = πriçindeki alanı = a 2 taralı = 128 cm 2 Dairenin alanından karenin 1. Karenin alanını çıkartırsak alanları elde ederiz. 2. Dairenin alanı = πr 2 = 32π 2. Karenin alanı = a 2 = 64 cm 2 3. Dairenin alanı = πr 2 = 16π 3. Karenin alanı = a 2 = 32 cm 2 D = 64π. K =128π =256 Taralı alan = 128π – 256 Ana Sayfaya Geri Dön
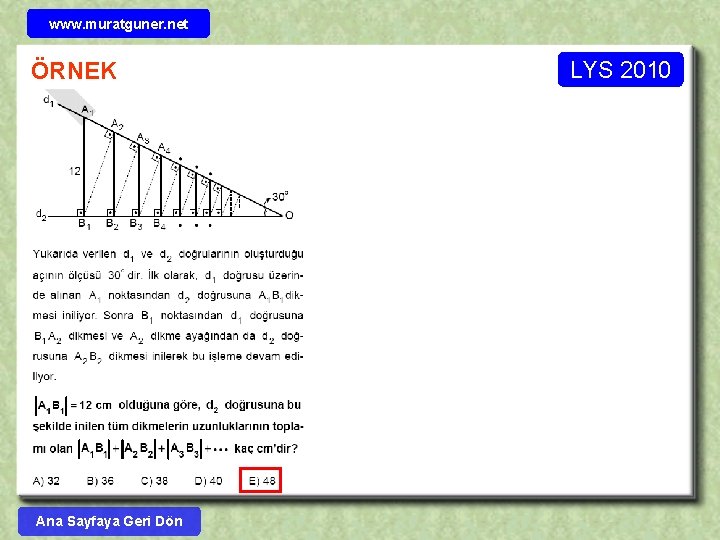
www. muratguner. net ÖRNEK Ana Sayfaya Geri Dön LYS 2010

www. muratguner. net ÖRNEK Ana Sayfaya Geri Dön LYS 2011
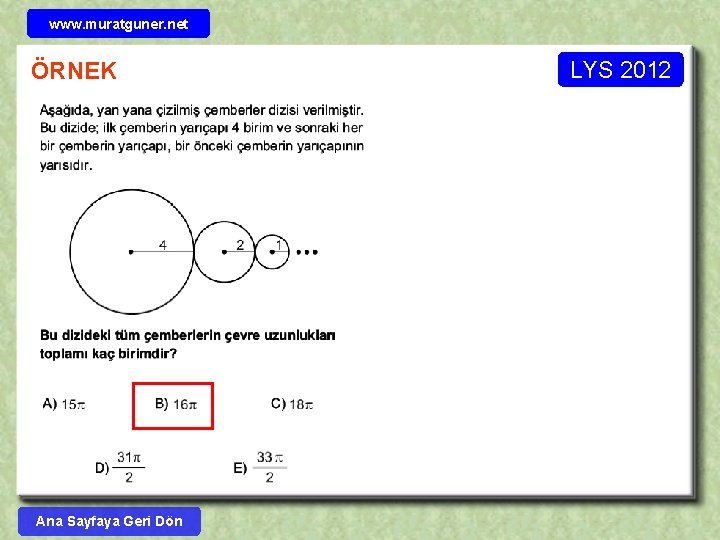
www. muratguner. net ÖRNEK Ana Sayfaya Geri Dön LYS 2012

KAYNAKÇA : 1 - MATEMATİK VADİSİ YAYINLARI 11. SINIF MATEMATİK 2 - ALTIN KİTAPLAR YAYINLARI LİSE-3 MATEMATİK 3 - MEB 11. SINIF MATEMATİK KİTABI DERS KİTABI 4 - BİREY YAYINLARI 11. SINIF MAEMATİK 5 - KAREKÖK YAYINLARI MATEMATİK – 4 6 - İNKILAP YAYINLARI LİSE-3 MATEMATİK 7 - KÜRE YAYINLARI LİSE-3 MATEMATİK 8 - FEM YAYINLARI 11. SINIF MATEMATİK 9 - AÇI YAYINLARI 11. SINIF MATEMATİK 10 - UĞUR YAYINLARI MATEMATİK 11 - FEM ÖĞRETMEN DERGİSİ 12 - SINAV DERGİSİ Ana Sayfaya Geri Dön
- Slides: 75