Wstp do optyki wspczesnej Krystyna Kolwas Instytut Fizyki

Wstęp do optyki współczesnej Krystyna Kolwas Instytut Fizyki PAN, ON 2. 2 Budynek VIII, pokój 4. www. ifpan. edu. pl/ON-2/on 22/modernoptics/

Wstęp do optyki współczesnej Indeks terminów i nazw dotychczas omówionych: n n n doświadczenie Michelsona-Morleya, doświadczenie Younga, korpuskularno-falowa teoria światła prawo Snella, zasada Huygensa,

Fale

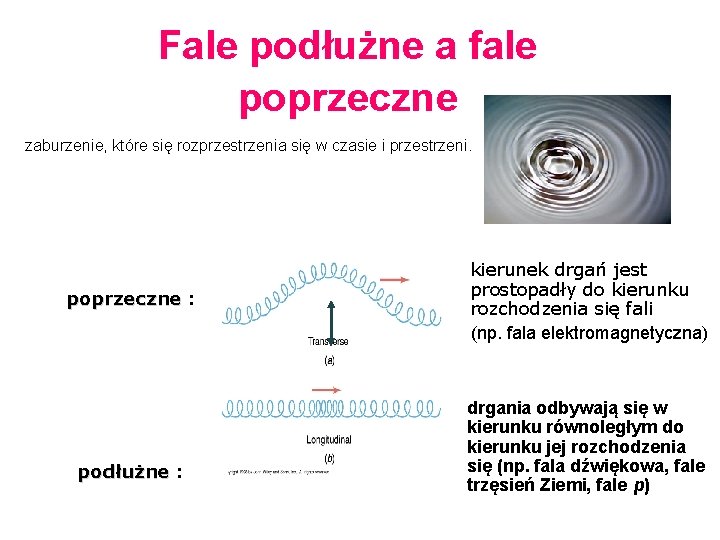
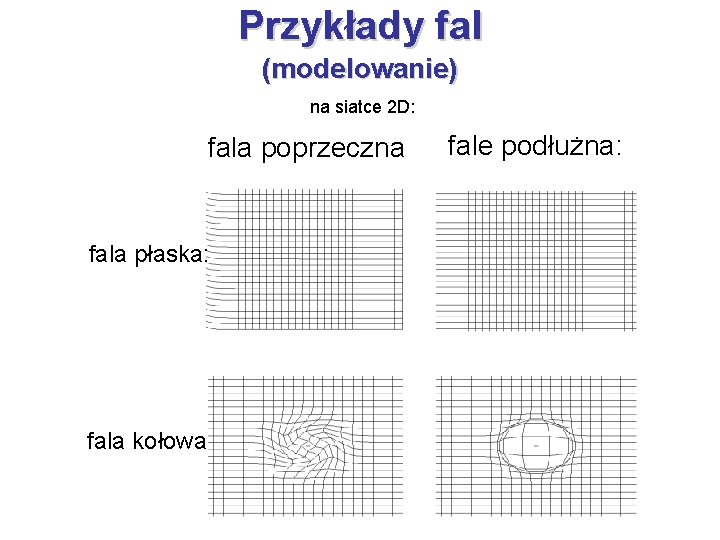
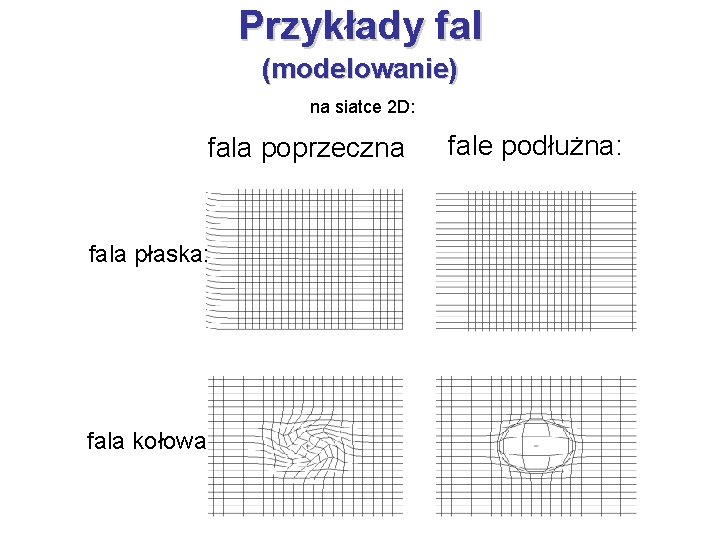
Fale podłużne a fale poprzeczne zaburzenie, które się rozprzestrzenia się w czasie i przestrzeni. Fala powierzchniowa na wodzie poprzeczne : podłużne : kierunek drgań jest prostopadły do kierunku rozchodzenia się fali (np. fala elektromagnetyczna) drgania odbywają się w kierunku równoległym do kierunku jej rozchodzenia się (np. fala dźwiękowa, fale trzęsień Ziemi, fale p)

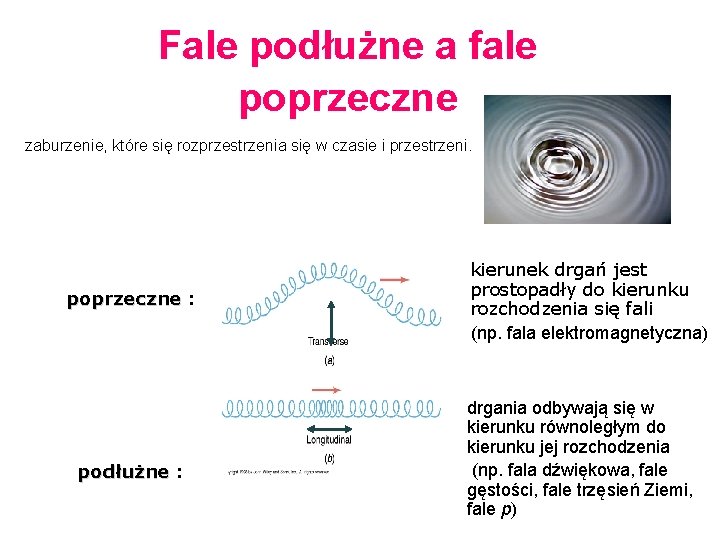
Fale podłużne a fale poprzeczne zaburzenie, które się rozprzestrzenia się w czasie i przestrzeni. poprzeczne : podłużne : kierunek drgań jest prostopadły do kierunku rozchodzenia się fali (np. fala elektromagnetyczna) drgania odbywają się w kierunku równoległym do kierunku jej rozchodzenia się (np. fala dźwiękowa, fale trzęsień Ziemi, fale p)

Fale podłużne a fale poprzeczne zaburzenie, które się rozprzestrzenia się w czasie i przestrzeni. poprzeczne : podłużne : kierunek drgań jest prostopadły do kierunku rozchodzenia się fali (np. fala elektromagnetyczna) drgania odbywają się w kierunku równoległym do kierunku jej rozchodzenia (np. fala dźwiękowa, fale gęstości, fale trzęsień Ziemi, fale p)

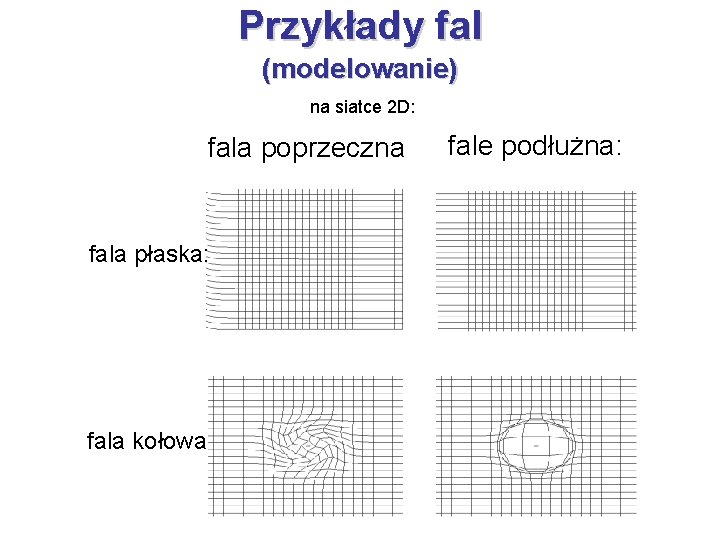
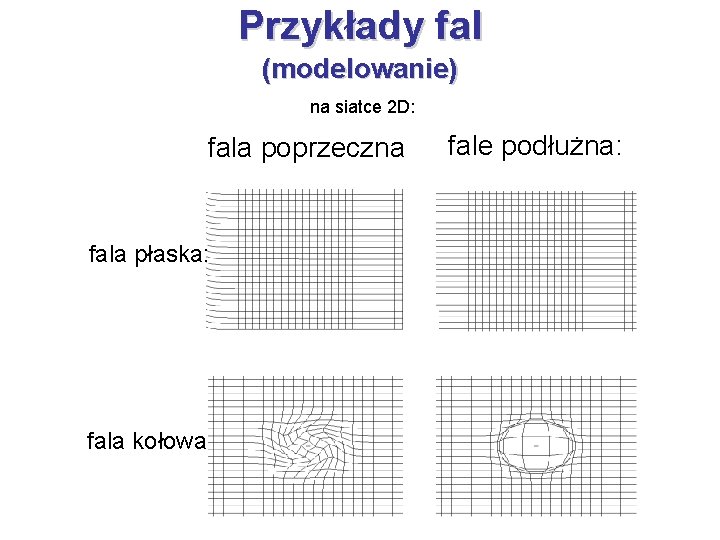
Przykłady fal (modelowanie) na siatce 2 D: fala poprzeczna fala płaska: fala kołowa fale podłużna:

Przykłady fal (modelowanie) na siatce 2 D: fala poprzeczna fala płaska: fala kołowa fale podłużna:

Przykłady fal (modelowanie) na siatce 2 D: fala poprzeczna fala płaska: fala kołowa fale podłużna:

Przykłady fal (modelowanie) na siatce 2 D: fala poprzeczna fala płaska: fala kołowa fale podłużna:

Przykłady fal (modelowanie) Impuls wędrujący wzdłuż struny zamocowanej z dwóch stron Fala stojąca Paczka falowa (suma wielu fal) (mechanika kwantowa!)

Przykłady fal: * Fale morskie czy oceaniczne: zaburzenie propagujące się w wodzie * Fale elektromagnetyczne: mogą propagować się w próżni (c=299 792 458 m/s) * Fale dźwiękowe — fale mechaniczne propagujące się w gazach, cieczach i ciałach stałych * Fale sejsmiczne (3 typy: S, P i L) * Fale grawitacyjne – nieliniowe fluktuacje w krzywiźnie czasoprzestrzeni, przewidziane w Ogólnej Teorii Względności, nie wykryte w doświadczeniach * Wewnętrzne fale w wirujących cieczach (efekt Coriolisa)

Równanie falowe Jednowymiarowe skalarne równanie falowe funkcji f : Skalarne równanie różniczkowe cząstkowe drugiego rzędu, opisujące propagację różnorodnych fal (elektromagnetycznych, dźwiękowych, fal wody, wibracje struny). Zastosowania: akustyka, elektromagnetyzm, dynamika cieczy… Fale elektromagnetyczne (w tym pole elektryczne E fali świetlnej) są rozwiązaniem równania falowego z v = c (w próżni). Równanie falowe można wyprowadzić z równań Maxwella.

Równanie falowe Jednowymiarowe skalarne równanie falowe posiada proste rozwiązanie: gdzie f (u) może być dowolną funkcją podwójnie różniczkowalną.

Fale: parametryzacja Najbardziej elementarna funkcja jednowymiarowa spełniająca równanie falowe: E(x, t) = EA 0 cos[(k x – t ) – ] A - amplituda - faza początkowa (faza absolutna) = 0 = 3/2 p

Fale: parametryzacja Najbardziej elementarna funkcja jednowymiarowa spełniająca równanie falowe: E(x, t) = EA 0 cos[(k x – t ) – ] A - amplituda - faza początkowa p Oscylacje w czasie i przestrzeni

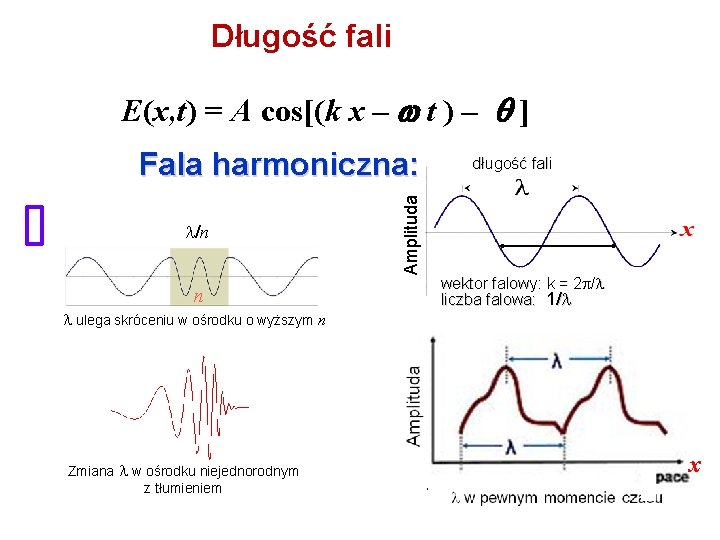
Fala harmoniczna E(x, t) = A cos[(k x – t ) – długość fali Amplituda wielkości przestrzenne: ] wektor falowy: k = 2 / liczba falowa: 1/ wielkości czasowe: Amplituda okres fali T częstość kołowa: =2 /T częstość: =1/T /T

Długość fali E(x, t) = A cos[(k x – t ) – /n Amplituda Fala harmoniczna: n ulega skróceniu w ośrodku o wyższym n ] długość fali wektor falowy: k = 2 / liczba falowa: 1/ Zmiana w ośrodku niejednorodnym z tłumieniem Amplituda okres fali częstość kołowa: =2 / częstość: =1/ x

Fala harmoniczna E(x, t) = A cos[(k x – t ) – Relacja dyspersji: długość fali Amplituda wielkości przestrzenne: ] w próżni: wektor falowy: k = 2 / liczba falowa: 1/ wielkości czasowe: Amplituda okres fali T częstość kołowa: =2 /T częstość: =1/T /T

Prędkość fazowa fali długość fali Z jaką prędkością przemieszcza się fala? Prędkość fazowa: prędkość z jaką rozchodzą się miejsca fali o tej samej fazie: vp = / T , lub: vp = / k W ośrodkach prędkość fazowa fali może być różna dla różnych częstotliwości. Mówi się wówczas, że dla tych fal zachodzi dyspersja; wówczas: a; = (k). Wówczas przemieszczanie się paczki falowej złożonych z fal o różnych opisuje dodatkowa wielkość: prędkość grupowa

Prędkość fazowa fali harmonicznej długość fali Z jaką prędkością przemieszcza się fala? Prędkość fazowa: prędkość z jaką rozchodzą się miejsca fali o tej samej fazie : vp = / T , lub: vp = / k W ośrodkach prędkość fazowa fali może być różna dla różnych Nie wystarczy, by opisać fale bardziej częstotliwości. Mówi się wówczas, że dla tych fal zachodzi dyspersja; wówczas: a; złożone! = (k). Wówczas przemieszczanie się paczki falowej złożonych z fal o różnych opisuje dodatkowa wielkość: prędkość grupowa

Prędkość fazowa fali harmonicznej -nie wystarczy, by opisać fale bardziej złożone! Paczka falowa złożona z fal o różnych : długość fali prędkość z jaką rozchodzą się miejsca fali o tej samej fazie: vp = / T , lub: vp = / k Przemieszczanie się paczki falowej złożonych z fal o różnych opisuje dodatkowa wielkość: prędkość grupowa: W ośrodkach dyspersyjnych fale o różnych częstotliwościach rozchodzą się z różnymi prędkościami fazowymi: vp = / k = /k 0 n ( ) =c 0 /n( ) Wówczas: = (k). vg º d /dk

Prędkość grupowa Dla fali harmonicznej o zmieniającej się (modulowanej) amplitudzie prędkość grupowa jest prędkością obwiedni fali nośnej: Obwiednia rozchodzi się z prędkością grupową: vg º d /dk Fala nośna rozchodzi się z prędkością fazową. vg vp Prędkość rozchodzenia się modulacji, czyli prędkość grupowa, odpowiada prędkości przenoszenia informacji i energii przez falę. Prędkość o której mowa w prawie załamania światła to też prędkość grupowa.

Prędkość grupowa wielkość opisująca rozchodzenie się fal nieharmonicznych. E(t) = A cos(j), j = k x – t – gdzie faza fali: j = j(x, y, z, t) (w przeciwieństwie do fazy początkowej ), Np. zmienia się w czasie i przestrzeni. Zmiany fazy w czasie: = – ¶j /¶t Zmiany fazy w przestrzeni: k = ¶j /¶x W języku fazy prędkość grupowa: Taka definicja jest przydatna dla naprawdę skomplikowanych fal.

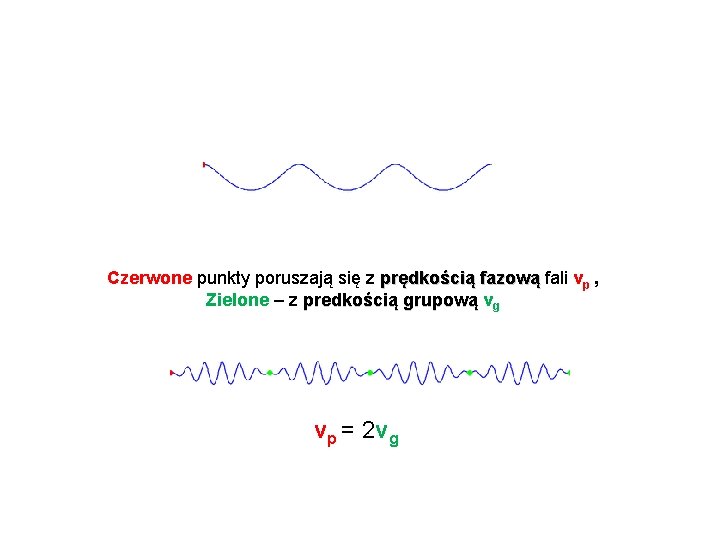
Czerwone punkty poruszają się z prędkością fazową fali v prędkością fazową p , Zielone – z predkością grupową v predkością grupową g vp = 2 vg

Prędkość grupowa fal w ośrodkach z dyspersją: n( ) vg º d /dk Częstość fali harmonicznej jest taka sama w ośrodku, jak i poza nim, Częstość /n ale: k = k 0 n = k 0 jest wektorem falowym w próżni, n n( ) jest parametrem (współczynnik załamania) zależnym od ośrodka. ulega skróceniu w ośrodku o wyższym n Tak więc wygodnie jest pomyśleć o jako o zmiennej niezależnej: Mamy więc: k = n( ) / c 0, pochodna k: dk /d = ( n + dn/d ) / c 0 vg = c 0 / ( n + dn/d ) = v = / k = c 0 /n, Ostatecznie: (c 0 /n) / (1 + /n dn/d ) vg = c 0 / (n + dn/d )

Prędkość grupowa fal w ośrodkach z dyspersją: n( ) vg º d /dk Częstość fali harmonicznej jest taka sama w ośrodku, jak i poza nim, Częstość ale: k = k 0 n = k 0 jest wektorem falowym w próżni, n( ) jest parametrem (współczynnik załamania) zależnym od ośrodka. Tak więc wygodnie jest pomyśleć o jako o zmiennej niezależnej: Mamy więc: k = n( ) / c 0, pochodna k: dk /d = ( n + dn/d ) / c 0 vg = c 0 / ( n + dn/d ) = v = / k = c 0 /n, Ostatecznie: (c 0 /n) / (1 + /n dn/d ) vg = c 0 / (n + dn/d )

Prędkość grupowa fal w ośrodkach z dyspersją: n( ) vg º d /dk Częstość fali harmonicznej jest taka sama w ośrodku, jak i poza nim, Częstość ale: k = k 0 n = k 0 jest wektorem falowym w próżni, n( ) jest parametrem (współczynnik załamania) zależnym od ośrodka. Tak więc wygodnie jest pomyśleć o jako o zmiennej niezależnej: Mamy więc: k = n( ) / c 0, pochodna k: dk /d = ( n + dn/d ) / c 0 vg = c 0 / ( n + dn/d ) = v = / k = c 0 /n, Ostatecznie: (c 0 /n) / (1 + /n dn/d ) vg = c 0 / (n + dn/d )

Prędkość grupowa fal w ośrodkach z dyspersją: n( ) vg º d /dk Częstość fali harmonicznej jest taka sama w ośrodku, jak i poza nim, Częstość ale: k = k 0 n = k 0 jest wektorem falowym w próżni, n( ) jest parametrem (współczynnik załamania) zależnym od ośrodka. Tak więc wygodnie jest pomyśleć o jako o zmiennej niezależnej: Mamy więc: k = n( ) / c 0, pochodna k: dk /d = ( n + dn/d ) / c 0 vg = c 0 / ( n + dn/d ) = v = / k = c 0 /n, Ostatecznie: (c 0 /n) / (1 + /n dn/d ) - prędkość światła w próżni zmniejszona przez wsp. załamania vg = c 0 / (n + dn/d )

Prędkość grupowa fal w ośrodkach z dyspersją: n( ) vg º d /dk Częstość fali harmonicznej jest taka sama w ośrodku, jak i poza nim, Częstość ale: k = k 0 n = k 0 jest wektorem falowym w próżni, n( ) jest parametrem (współczynnik załamania) zależnym od ośrodka. Tak więc wygodnie jest pomyśleć o jako o zmiennej niezależnej: Mamy więc: k = n( ) / c 0, pochodna k: dk /d = ( n + dn/d ) / c 0 vg = c 0 / ( n + dn/d ) = v = / k = c 0 /n, Ostatecznie: (c 0 /n) / (1 + /n dn/d ) - prędkość światła w próżni zmniejszona przez wsp. załamania vg = c 0 / (n + dn/d )

Prędkość grupowa fal w ośrodkach z dyspersją: n( ) vg º d /dk Częstość fali harmonicznej jest taka sama w ośrodku, jak i poza nim, Częstość ale: k = k 0 n = k 0 jest wektorem falowym w próżni, n( ) jest parametrem (współczynnik załamania) zależnym od ośrodka. Tak więc wygodnie jest pomyśleć o jako o zmiennej niezależnej: Mamy więc: k = n( ) / c 0, pochodna k: dk /d = ( n + dn/d ) / c 0 vg = c 0 / ( n + dn/d ) = v p = / k = c 0 /n, Ostatecznie: (c 0 /n) / (1 + /n dn/d ) - prędkość światła w próżni zmniejszona przez wsp. załamania vg = c 0 / (n + dn/d )

Prędkość grupowa a dyspersja ośrodka: n( ) vg º d /dk Częstość fali harmonicznej jest taka sama w rozważanym ośrodku, jak i poza nim, ale k = k 0 n, gdzie k 0 jest wektorem falowym w próżni i n jest vg = v parametrem (współczynnik załamania) zależnym od ośrodka. Tak więc wygodnie jest pomyśleć o jako o zmiennej niezależnej: Ponieważ: k = n( ) / c 0, pochodna k: dk /d = ( n + dn/d ) / c 0 vg = c 0 / ( n + dn/d ) = v p = / k = c 0 /n, (c 0 /n) / (1 + /n dn/d ) vg = c 0 / (n + dn/d ) Prędkość grupowa równa jest prędkości fazowej, gdy dn/d = 0, (brak dyspersji, tak jak np. w próżni).

W ośrodku dyspersyjnym: fale harmoniczne o różnych częstościach rozchodzą się z różnymi prędkościami. Każda ze składowych harmonicznych rozchodzi się ze zwykłą prędkością fazową (falową): vp = / k, natomiast paczka fal jako całość przesuwa vp. się z prędkością vg Falę taką opisać możemy jako falę harmoniczną o zmieniającej się (modulowanej) amplitudzie; prędkość rozchodzenia się grzbietów Fala będąca paczką fal zawierających częstości z modulacji to prędkość grupowa: pewnego przedziału będzie więc zmieniać swój kształt. vg = d /dk.

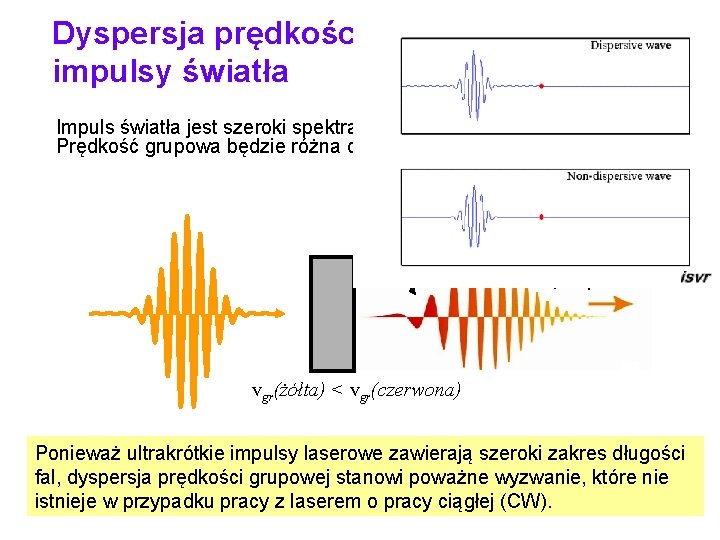
Dyspersja prędkości grupowej a impulsy światła Impuls światła jest szeroki spektralnie (zawiera wiele częstości). Prędkość grupowa będzie różna dla różnych długości światła. czasowy początek impulsu czasowy koniec impulsu vgr(żółta) < vgr(czerwona) Ponieważ ultrakrótkie impulsy laserowe zawierają szeroki zakres długości fal, dyspersja prędkości grupowej stanowi poważne wyzwanie, które nie istnieje w przypadku pracy z laserem o pracy ciągłej (CW).

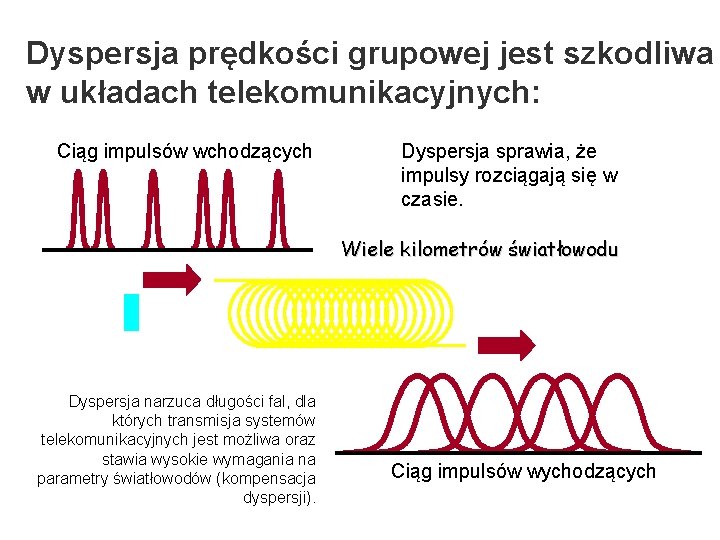
Dyspersja prędkości grupowej jest szkodliwa w układach telekomunikacyjnych: Ciąg impulsów wchodzących Dyspersja sprawia, że impulsy rozciągają się w czasie. Wiele kilometrów światłowodu Dyspersja narzuca długości fal, dla których transmisja systemów telekomunikacyjnych jest możliwa oraz stawia wysokie wymagania na parametry światłowodów (kompensacja dyspersji). Ciąg impulsów wychodzących

Czy można: • zatrzymać światło? • przyspieszyć światło? !?

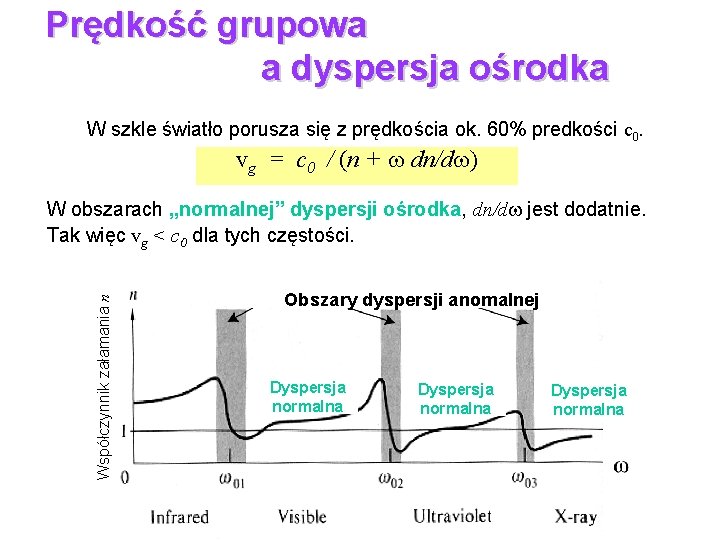
Prędkość grupowa a dyspersja ośrodka Prędkość grupowa jest mniejsza niż prędkość fazowa w obszarach W szkle światło porusza się z prędkościa ok. 60% predkości c 0. częstości, dla których dany ośrodek nie absorbuje światła. vg = c 0 / (n + dn/d ) Współczynnik załamania n W obszarach „normalnej” dyspersji ośrodka, dn/d jest dodatnie. Tak więc vg < c 0 dla tych częstości. Obszary dyspersji anomalnej Dyspersja normalna

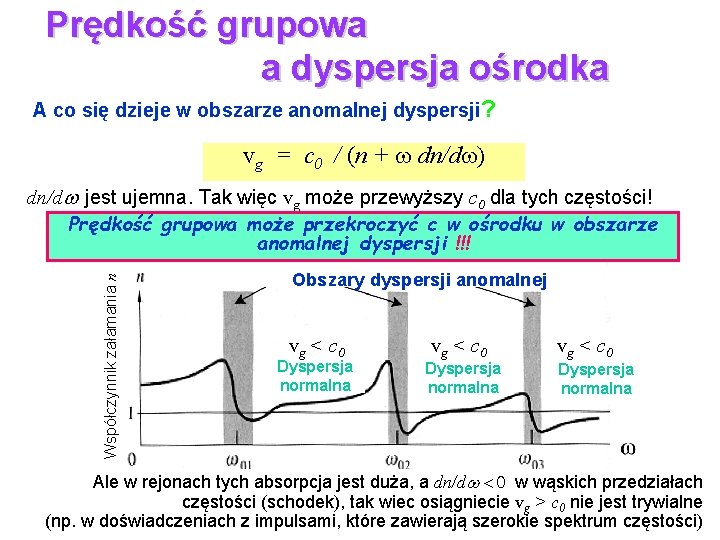
Prędkość grupowa a dyspersja ośrodka A co się dzieje w obszarze anomalnej dyspersji? vg = c 0 / (n + dn/d ) Współczynnik załamania n dn/d jest ujemna. Tak więc vg może przewyższy c 0 dla tych częstości! Prędkość grupowa może przekroczyć c w ośrodku w obszarze anomalnej dyspersji !!! Obszary dyspersji anomalnej vg < c 0 Dyspersja normalna Ale w rejonach tych absorpcja jest duża, a dn/d < 0 w wąskich przedziałach częstości (schodek), tak wiec osiągniecie vg > c 0 nie jest trywialne (np. w doświadczeniach z impulsami, które zawierają szerokie spektrum częstości)

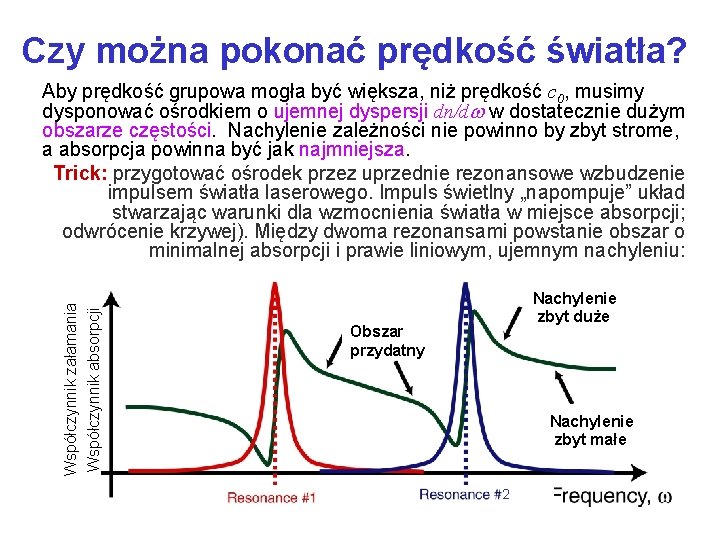
Czy można pokonać prędkość światła? Współczynnik załamania Współczynnik absorpcji Aby prędkość grupowa mogła być większa, niż prędkość c 0, musimy dysponować ośrodkiem o ujemnej dyspersji dn/d w dostatecznie dużym obszarze częstości. Nachylenie zależności nie powinno by zbyt strome, a absorpcja powinna być jak najmniejsza. Trick: przygotować ośrodek przez uprzednie rezonansowe wzbudzenie impulsem światła laserowego. Impuls świetlny „napompuje” układ stwarzając warunki dla wzmocnienia światła w miejsce absorpcji; odwrócenie krzywej). Między dwoma rezonansami powstanie obszar o minimalnej absorpcji i prawie liniowym, ujemnym nachyleniu: Nachylenie zbyt duże Obszar przydatny Nachylenie zbyt małe 2

Czy można pokonać prędkość światła? Współczynnik załamania Współczynnik absorpcji Aby prędkość grupowa mogła być większa, niż prędkość c 0, musimy dysponować ośrodkiem o ujemnej dyspersji dn/d w dostatecznie dużym obszarze częstości. Nachylenie zależności nie powinno by zbyt strome, a absorpcja powinna być jak najmniejsza. Trick: przygotować ośrodek przez uprzednie rezonansowe wzbudzenie impulsem światła laserowego. Impuls świetlny „napompuje” układ stwarzając warunki dla wzmocnienia światła w miejsce absorpcji; odwrócenie krzywej). Między dwoma rezonansami powstanie obszar o minimalnej absorpcji i prawie liniowym, ujemnym nachyleniu: Nachylenie zbyt duże Obszar przydatny Nachylenie zbyt małe 2

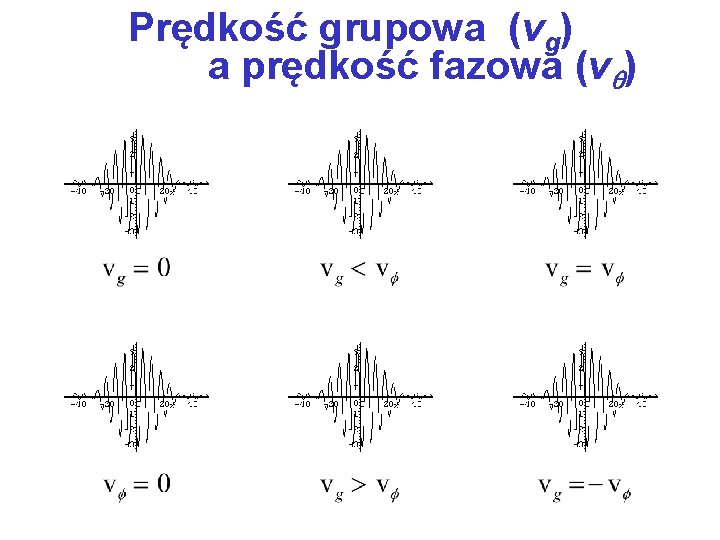
Prędkość grupowa (vg) a prędkość fazowa (v )

Zadania: 1. Wykaż, że gdy funkcja f (x) spełnia równanie falowe, funkcja f (x ± vt) również spełnia równanie falowe. 2. Sprawdź poprawność związków między prędkością fazową i prędkością grupową: Przedyskutuj ten związek dla ośrodków posiadających dyspersję czasową (w ośrodkach takich częstość zależy od długości fali ).

Opis fal przy pomocy liczb zespolonych Pole elektryczne fali świetlnej o częstości : E(x, t) = A cos(kx – t – ) Ponieważ exp(ij) = cos(j) + i sin(j) (formuła Eulera): E(x, t) = Re { A exp[i(kx – t – )] } lub E(x, t) = 1/2 A exp[i(kx – t – )] + c. c. Często wyrażenia te są zapisywane bez ½, Re, or +c. c. gdzie "+ c. c. " oznacza "plus oznacza sprzężenie zespolone wszystkiego, co jest przed plusem. Możemy wygodnie różniczkować exp(ikx):

Opis fal przy pomocy liczb zespolonych Pole elektryczne fali świetlnej o częstości : E(x, t) = A cos(kx – t – ) Ponieważ exp(ij) = cos(j) + i sin(j) (formuła Eulera ): E(x, t) = Re { A exp[i(kx – t – )] } lub E(x, t) = 1/2 A exp[i(kx – t – )] + c. c. Często wyrażenia te są zapisywane bez ½, Re, or +c. c. gdzie "+ c. c. " oznacza sprzężenie zespolone wszystkiego, co jest przed plusem. ):

Opis fal przy pomocy liczb zespolonych Pole elektryczne fali świetlnej o częstości można opisać: E(x, t) = A cos(kx – t – ) Ponieważ exp(ij) = cos(j) + i sin(j) (formuła Eulera ): E(x, t) = Re { A exp[i(kx – t – )] } E(x, t) = 1/2 A exp[i(kx – t – )] + c. c. lub gdzie "+ c. c. " oznacza sprzężenie zespolone wszystkiego, co jest przed plusem. Możemy wygodnie różniczkować exp(ikx):

Przypomnienie: liczby zespolone Każdą liczbę zespoloną z, można zapisać: Tak więc: i z = Re{ z } + i Im{ z } Re{ z } = 1/2 ( z + z* ) Im{ z } = 1/2 i ( z – z* ) gdzie z* jest liczbą sprzężoną liczby z ( i ® –i ) Wielkość | z | (moduł), liczby zespolonej: | z |2 = z z* = Re{ z }2 + Im{ z }2 Liczbęz zapisać można w postaci polarnej: A exp(ij). gdzie: A 2 = Re{ z }2 + Im{ z }2 tan(j) = Im{ z } / Re{ z }

Przypomnienie: liczby zespolone Każdą liczbę zespoloną z, można zapisać: Tak więc: i z = Re{ z } + i Im{ z } Re{ z } = 1/2 ( z + z* ) Im{ z } = 1/2 i ( z – z* ) gdzie z* jest liczbą sprzężoną liczby z ( i ® –i ) Wielkość | z | (moduł), liczby zespolonej: | z |2 = z z* = Re{ z }2 + Im{ z }2 Liczbę z zapisać można w postaci polarnej: A exp(ij). A 2 = Re{ z }2 + Im{ z }2 tan(j) = Im{ z } / Re{ z } z

Fale zapisane przy pomocy zespolonych amplitud W opisie fal wygodnie jest dopuścić zespolone amplitudy: Szybko-zmienne części zostały odseparowane od części stałych w czasie. W wyniku otrzymujemy „zespolone amplitudy": Tak więc: uwaga na Pole tak zapisane jest całkowicie zespolone! Jak odróżnić, E 0 jest rzeczywiste, czy zespolone? Nie wszyscy używają znaczka "~", by oznaczyć zespoloność amplitudy. Lepiej jest zawsze założyć, że jest zespolona.

Fale zapisane przy pomocy zespolonych amplitud W opisie fal wygodnie jest dopuścić zespolone amplitudy: Szybko-zmienne części zostały odseparowane od części stałych w czasie. W wyniku otrzymujemy „zespolone amplitudy": Tak więc: uwaga na Pole tak zapisane jest całkowicie zespolone! Jak odróżnić, E 0 jest rzeczywiste, czy zespolone? Nie wszyscy używają znaczka "~", by oznaczyć zespoloność amplitudy. Lepiej jest zawsze założyć, że jest zespolona.

Fale zapisane przy pomocy zespolonych amplitud W opisie fal wygodnie jest dopuścić zespolone amplitudy: Szybko-zmienne części zostały odseparowane od części stałych w czasie. W wyniku otrzymujemy „zespolone amplitudy": Tak więc: uwaga na Pole tak zapisane jest całkowicie zespolone! Jak odróżnić, E 0 jest rzeczywiste, czy zespolone? Nie wszyscy używają znaczka "~", by oznaczyć zespoloność amplitudy. Lepiej jest zawsze założyć, że jest zespolona.

Liczby zespolone w optyce ułatwiają życie Dodawanie fal o tych samych częstościach i różnych fazach początkowych daje falę o tej samej częstości. Nie jest to takie oczywiste w zapisie z użyciem funkcji trygonometrycznych, a jest natychmiastowe z użyciem eksponensów: gdzie wszystkie fazy początkowe zostały włączone w E 1, E 2, i E 3.

Fala płaska: Jest to fala o stałej częstotliwości, której powierzchnie falowe (powierzchne jednakowej fazy) tworzą równoległe do siebie płaszczyzny. Wypełniają one całą przestrzeń. Płaszczyzny frontów falowych fal elektromagnetycznych wędrują w próżni z prędkością światła. Płaszczyzny frontów falowych są odległe o długość fali. Są one prostopadłe do kierunku propagacji. Na oznaczenie fali płaskiej zazwyczaj rysujemy linie.

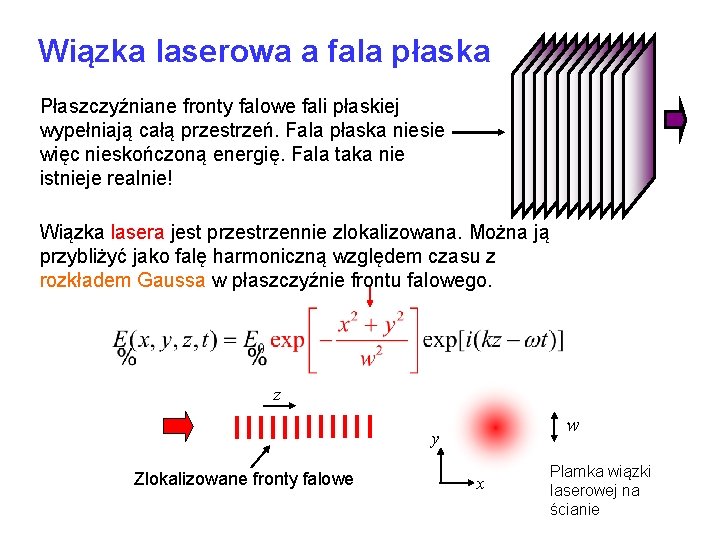
Wiązka laserowa a fala płaska Płaszczyźniane fronty falowe fali płaskiej wypełniają całą przestrzeń. Fala płaska niesie więc nieskończoną energię. Fala taka nie istnieje realnie! Wiązka lasera jest przestrzennie zlokalizowana. Można ją przybliżyć jako falę harmoniczną względem czasu z rozkładem Gaussa w płaszczyźnie frontu falowego. z w y Zlokalizowane fronty falowe x Plamka wiązki laserowej na ścianie

Wiązka laserowa a fala płaska Płaszczyźniane fronty falowe fali płaskiej wypełniają całą przestrzeń. Fala płaska niesie więc nieskończoną energię. Fala taka nie istnieje realnie! Wiązka lasera jest przestrzennie zlokalizowana. Można ją przybliżyć jako falę harmoniczną względem czasu z rozkładem Gaussa w płaszczyźnie frontu falowego. z w y Zlokalizowane fronty falowe x Plamka wiązki laserowej na ścianie

Równania Maxwella Podstawowe równania elektromagnetyzmu i optyki. Opisują własności pola elektrycznego i magnetycznego oraz zależności między tymi polami. W próżni (w powietrzu): - natężenie pola elektrycznego, [ V / m ], - indukcja magnetyczna, [T = Vs /m 2 ], e 0 - przenikalność elektryczna, m 0 - przenikalność magnetyczna, - operator dywergencji, [1/m], - operator rotacji, [1/m]. Z równań Maxwella można wyprowadzić równanie falowe fali elektromagnetycznej.

Równania Maxwella Podstawowe równania elektromagnetyzmu i optyki. Opisują własności pola elektrycznego i magnetycznego oraz zależności między tymi polami. W ośrodkach liniowych: sformułowanie „makroskopowe” - natężenie pola elektrycznego, [ V / m ], - indukcja magnetyczna, [ T = Vs /m 2], - indukcja elektryczna, [ C / m 2] - natężenie pola magnetycznego, [ A / m ] er - przenikalność elektryczna ośrodka, mr - przenikalność magnetyczna ośrodka, - gęstość prądu swobodnego, [A/m 2], - gęstość ładunku swobodnego, [ C / m 3] - operator dywergencji, [1/m], - operator rotacji, [1/m].

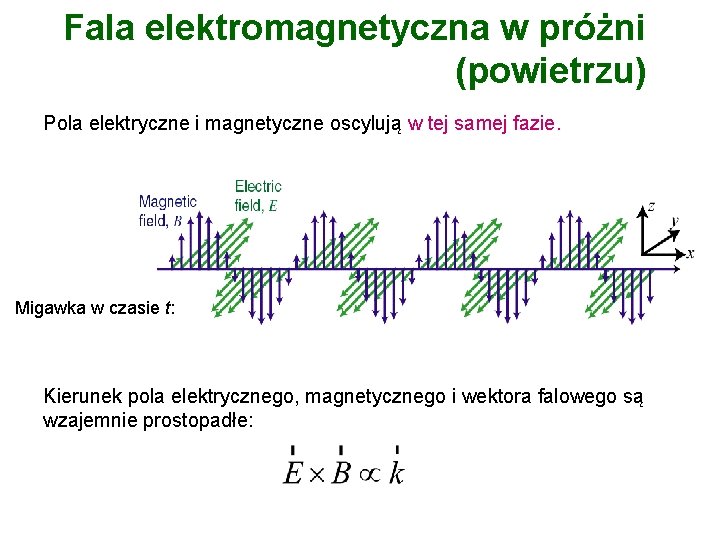
Fala elektromagnetyczna w próżni (powietrzu) Pola elektryczne i magnetyczne oscylują w tej samej fazie. Migawka w czasie t: Kierunek pola elektrycznego, magnetycznego i wektora falowego są wzajemnie prostopadłe:

Światło jest nie tylko falą, ale i cząstką. Fotografie wykonane przyciemnianym świetle są bardziej ziarniste. Jeśli badamy światło bardzo słabe, możemy się przekonać, że składa się ono z cząstek zwanych fotonami.

Fotony Foton posiada energię: i pęd: Wielkość pędu wynosi: , gdzie: h jest stałą Plancka, k jest wektorem falowym (o liczbie falowej k=2 / , ), ) jest częstością kołową. Wektor k wskazuje kierunek propagacji.

Fotony Foton posiada energię: i pęd: Wielkość pędu wynosi: , gdzie: W pustej przestrzeni foton porusza się z prędkością światła c i jego energia E i pęd p powiązane są relacją: E=cp Dla porównania, odpowiadający temu związek energii i pędu dla cząstki posiadającej masę byłby: E 2= (cp)2+(mc 2)2 (szczególna teoria względności).

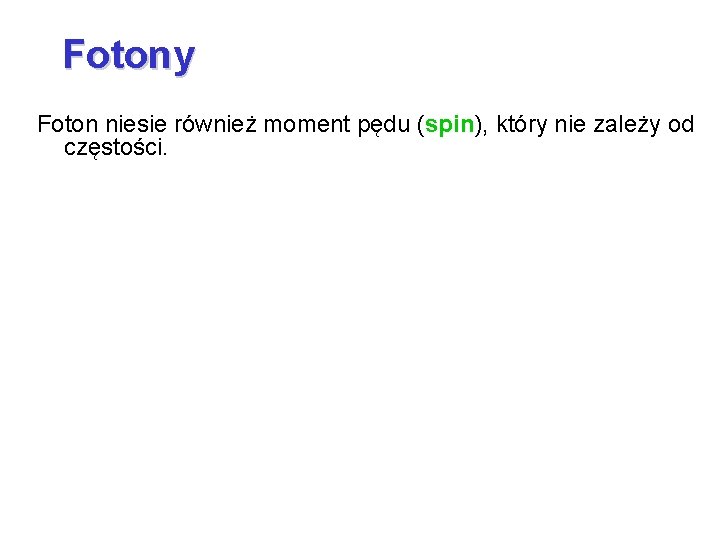
Fotony Foton niesie również moment pędu (spin), który nie zależy od częstości.

Fotony Foton niesie również moment pędu (spin), który nie zależy od częstości. Długość momentu pędu wynosi , tak więc jego składowe mierzone wzdłuż kierunku ruchu (jego skrętności) wynoszą odpowiednio . Wartości te odpowiadają dwóm możliwym stanom polaryzacji kołowej (lewo- i prawo-skrętnej). Polaryzacja liniowa to superpozycja tych polaryzacji. Foton posiada więc spin całkowity (jest bozonem), podlega więc statystyce Bosego–Einsteina. Dowolna liczba bozonów może dzielić ten sam stan kwantowy.

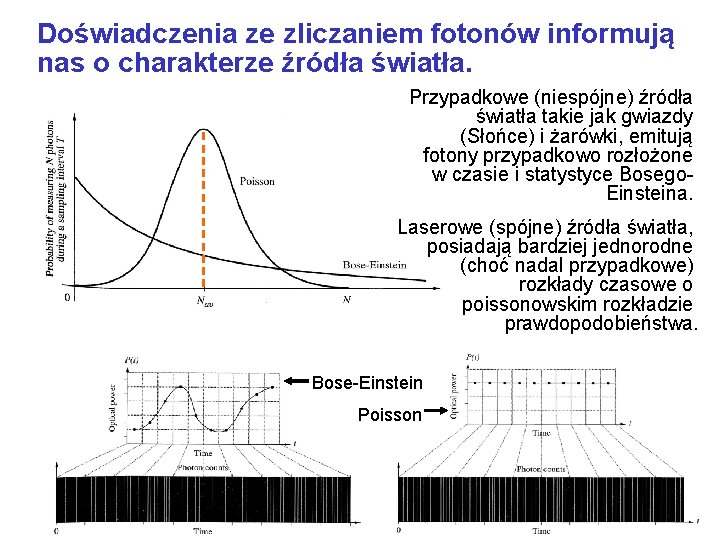
Doświadczenia ze zliczaniem fotonów informują nas o charakterze źródła światła. Przypadkowe (niespójne) źródła światła takie jak gwiazdy (Słońce) i żarówki, emitują fotony przypadkowo rozłożone w czasie i statystyce Bosego. Einsteina. Laserowe (spójne) źródła światła, posiadają bardziej jednorodne (choć nadal przypadkowe) rozkłady czasowe o poissonowskim rozkładzie prawdopodobieństwa. Bose-Einstein Poisson

Pęd fotonów w oddziaływaniu z atomami Jeśli atom emituje foton, podlega odrzutowi w przeciwnym kierunku, zgodnie z zasada zachowania pędu. Jeśli atomy zostaną wzbudzone, a następnie emitują światło, wiązka atomowa stanie się bardziej rozbieżna, niż wiązka atomów przed wzbudzeniem światłem.

Fotony – ciśnienie światła Fotony nie mają masy, ale po zaabsorbowaniu przez przekazują swój pęd. Promieniowanie słoneczne trafiające na Ziemię ma gęstość energii strumienia pola równą 1370 W/m 2, więc ciśnienie promieniowania (gdyby zostało całkowicie pochłonięte) wynosi: P= S/c P (1400 W/m 2)/(3 x 108 m/s) 5 x 10 -6 Pa << Patm= 105 Pa Żagle słoneczne, zaproponowane jako metoda napędu misji kosmicznych używałyby ciśnienia promieniowania Słońca jako siłę napędową. Ciśnienie promieniowania jest niezaniedbywalne: • Odchylanie warkoczy komet (pozostałe siły są mniejsze) • Statek kosmiczny Viking (minąłby Marsa o 15, 000 km) • Wnętrz gwiazd

Fotony – ciśnienie światła Fotony nie mają masy, ale po zaabsorbowaniu przez przekazują swój pęd. Promieniowanie słoneczne trafiające na Ziemię ma gęstość energii strumienia pola równą 1370 W/m 2, więc ciśnienie promieniowania (gdyby zostało całkowicie pochłonięte) wynosi: P= S/c P (1400 W/m 2)/(3 x 108 m/s) 5 x 10 -6 Pa << Patm= 105 Pa Żagle słoneczne, zaproponowane jako metoda napędu misji kosmicznych używałyby ciśnienia promieniowania Słońca jako siłę napędową. Ciśnienie promieniowania jest niezaniedbywalne: • Odchylanie warkoczy komet (pozostałe siły są mniejsze) • Statek kosmiczny Viking (minąłby Marsa o 15, 000 km)

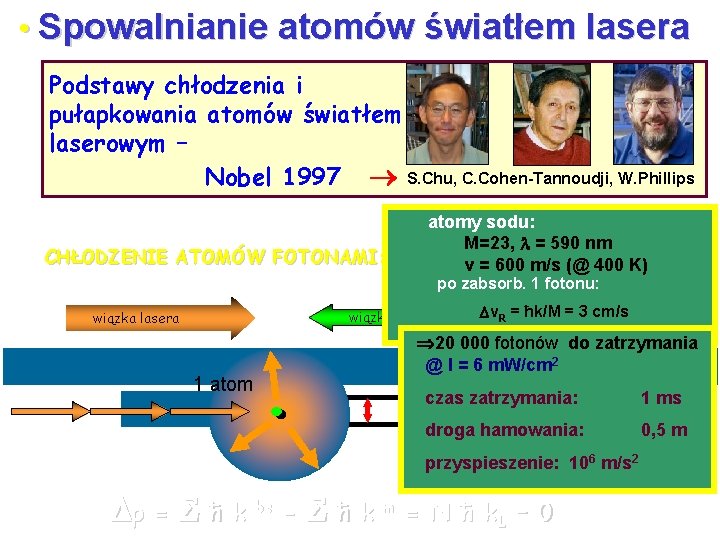
• Spowalnianie atomów światłem lasera Podstawy chłodzenia i pułapkowania atomów światłem laserowym – Nobel 1997 S. Chu, C. Cohen-Tannoudji, W. Phillips CHŁODZENIE ATOMÓW FOTONAMI: atomy sodu: M=23, = 590 nm v = 600 m/s (@ 400 K) po zabsorb. 1 fotonu: wiązka atomów wiązka lasera v. R = ħk/M = 3 cm/s 20 000 fotonów do zatrzymania @ I = 6 m. W/cm 2 1 atom czas zatrzymania: 1 ms droga hamowania: 0, 5 m przyspieszenie: 106 m/s 2 p = ħ kabs - ħ kem = N ħ k. L – 0

Pułapki magneto-optyczne umożliwiają ochłodzenie chmury (gazu) neutralnych atomów do temperatur rzędu 100µK PUŁAPKA MOT IF PAN (M. Głóź) IF UW (W. Gawlik) Laboratorium FAMO (Toruń) Chmura zimnych atomów Rb w centrum pułapki

Photons "What is known [of photons] comes from observing the results of their being created or annihilated. " Eugene Hecht Można powiedzieć, że zdanie to jest słuszne nie tylko dla fotonów, ale dla wszystkiego, co jesteśmy w stanie zaobserwować. Nasz ogląd świata jest wynikiem kreowania i anihilowania fotonów, czyli sposobu, w jaki światło oddziałuje z materią.

Indeks haseł dotychczas omówionych: • • doświadczenie Michelsona. Morleya, doświadczenie Younga, prawo Snella, zasada Huygensa • • • • Chłodzenie atomów światłem laserowym Ciśnienie światła Dyspersja (czasowa) Dyspersja prędkości grupowej Fala elektromagnetyczna Fale podłużne Fale poprzeczne Prędkość fazowa Prędkość grupowa Równania Maxwella w próżni Równania Maxwella w ośrodkach materialnych Równanie falowe skalarne Spin fotonu Światło jako fala elektromagnetyczna Światło jako strumień fotonów

Dziękuję za uwagę

Zadania: 1. Wykaż, że gdy funkcja f (x) spełnia równanie falowe, funkcja f (x ± vt) również spełnia równanie falowe. 2. Sprawdź poprawność związków między prędkością fazową i prędkością grupową:

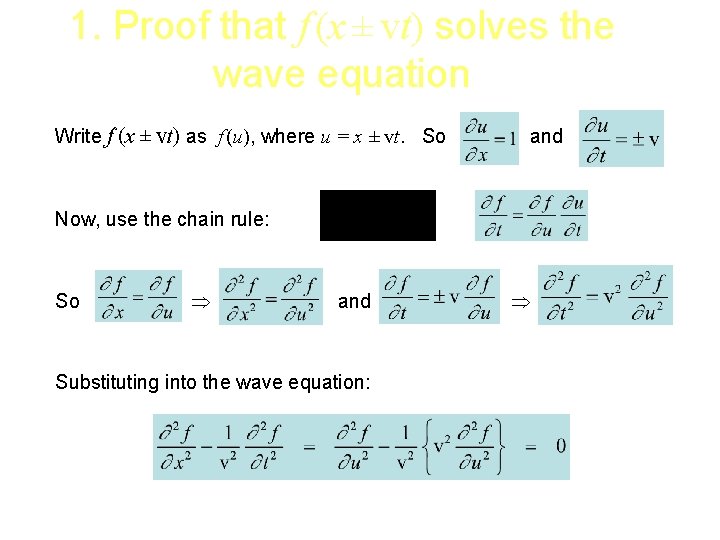
1. Proof that f (x ± vt) solves the wave equation Write f (x ± vt) as f (u), where u = x ± vt. So and Now, use the chain rule: So Þ and Þ Substituting into the wave equation: