WRS Waiting Room Sampling for Accurate Triangle Counting

WRS: Waiting Room Sampling for Accurate Triangle Counting in Real Graph Streams Kijung Shin

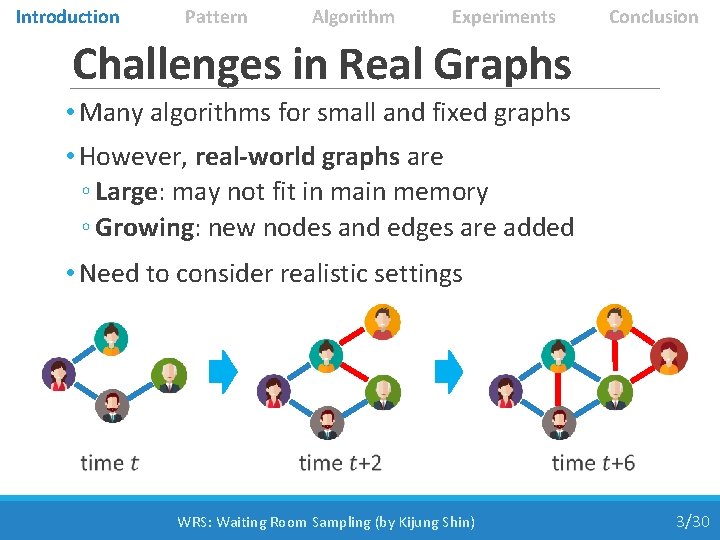
Introduction Pattern Algorithm Experiments Conclusion Triangles in a Graph • Graphs are everywhere! ◦ Social Network, Web, Emails, etc. • Triangles are a fundamental primitive ◦ 3 nodes connected to each other • Counting triangles has many applications ◦ Community detection, Spam detection, Query optimization WRS: Waiting Room Sampling (by Kijung Shin) 2/30

Introduction Pattern Algorithm Experiments Conclusion Challenges in Real Graphs • Many algorithms for small and fixed graphs • However, real-world graphs are ◦ Large: may not fit in main memory ◦ Growing: new nodes and edges are added • Need to consider realistic settings WRS: Waiting Room Sampling (by Kijung Shin) 3/30

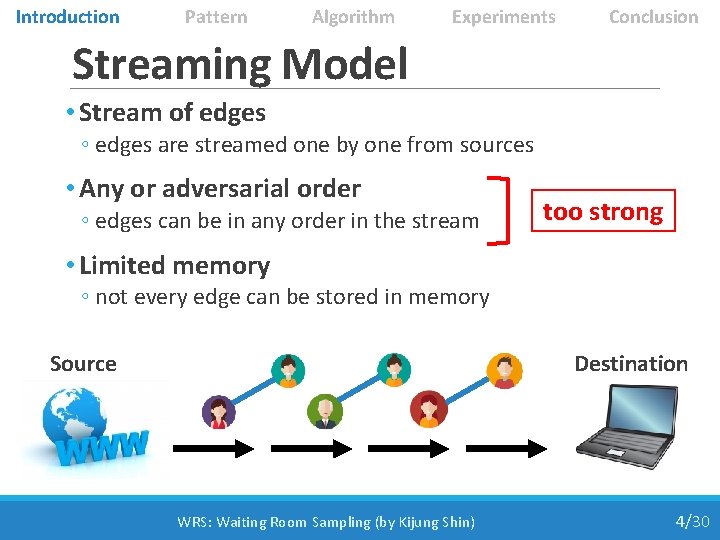
Introduction Pattern Algorithm Experiments Conclusion Streaming Model • Stream of edges ◦ edges are streamed one by one from sources • Any or adversarial order ◦ edges can be in any order in the stream too strong • Limited memory ◦ not every edge can be stored in memory Source Destination WRS: Waiting Room Sampling (by Kijung Shin) 4/30

Introduction Pattern Algorithm Experiments Conclusion Relaxed Streaming Model • Stream of edges ◦ edges are streamed one by one from sources • Chronological order ◦ natural for dynamic graphs ◦ edges are streamed when they are created • Limited memory ◦ not every edge can be stored in memory “What temporal patterns do exist? ” “How can we exploit them for accurate triangle counting? ” WRS: Waiting Room Sampling (by Kijung Shin) 5/30

Roadmap • Introduction • Temporal Pattern << • Proposed Algorithm • Experiments • Conclusion WRS: Waiting Room Sampling (by Kijung Shin) 6/30

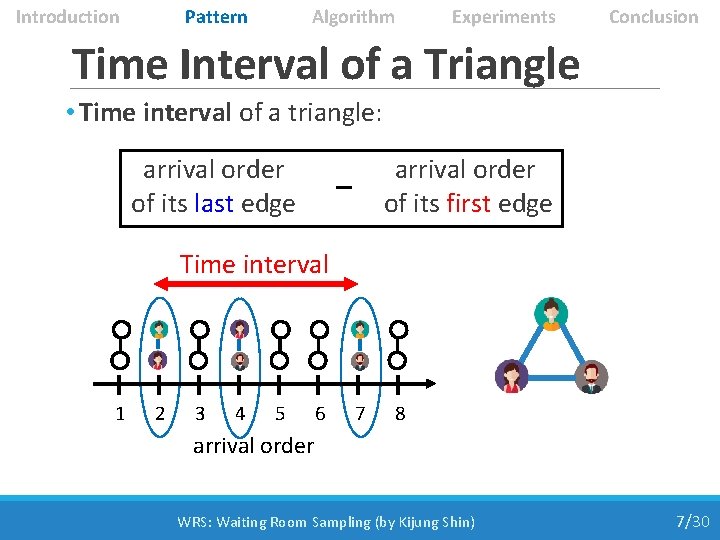
Introduction Pattern Algorithm Experiments Conclusion Time Interval of a Triangle • Time interval of a triangle: arrival order of its last edge – arrival order of its first edge Time interval 1 2 3 4 5 6 7 8 arrival order WRS: Waiting Room Sampling (by Kijung Shin) 7/30

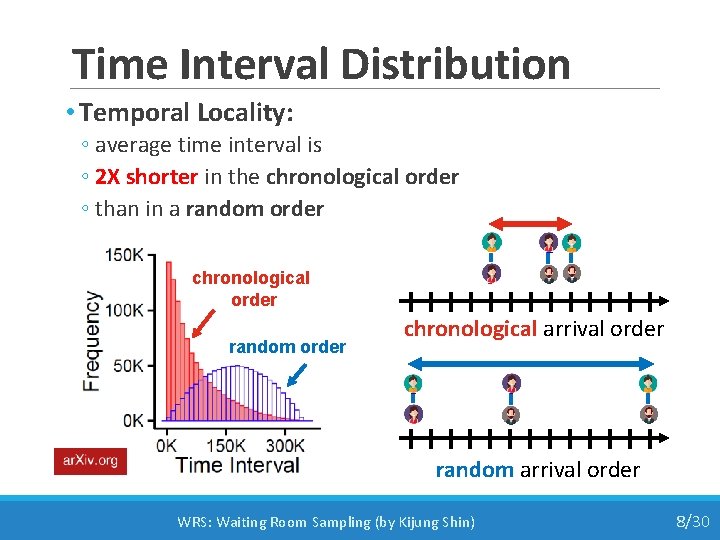
Time Interval Distribution • Temporal Locality: ◦ average time interval is ◦ 2 X shorter in the chronological order ◦ than in a random order chronological order random order chronological arrival order random arrival order WRS: Waiting Room Sampling (by Kijung Shin) 8/30

Introduction Pattern Algorithm Experiments Conclusion Temporal Locality (cont. ) • One interpretation: ◦ edges are more likely to form ◦ triangles with edges close in time ◦ than with edges far in time chronological order random order • Another interpretation: ◦ new edges are more likely to form ◦ triangles with recent edges ◦ than with old edges “How can we exploit temporal locality for accurate triangle counting? ” WRS: Waiting Room Sampling (by Kijung Shin) 9/30

Roadmap • Introduction • Temporal Pattern • Proposed Algorithm << • Experiments • Conclusion WRS: Waiting Room Sampling (by Kijung Shin) 10/30

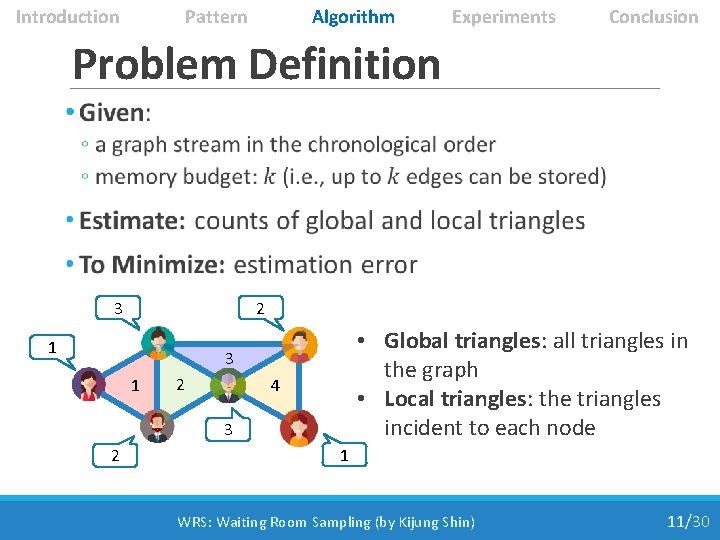
Introduction Pattern Algorithm Experiments Conclusion Problem Definition • 3 2 1 • Global triangles: all triangles in the graph • Local triangles: the triangles incident to each node 3 1 2 4 3 2 1 WRS: Waiting Room Sampling (by Kijung Shin) 11/30

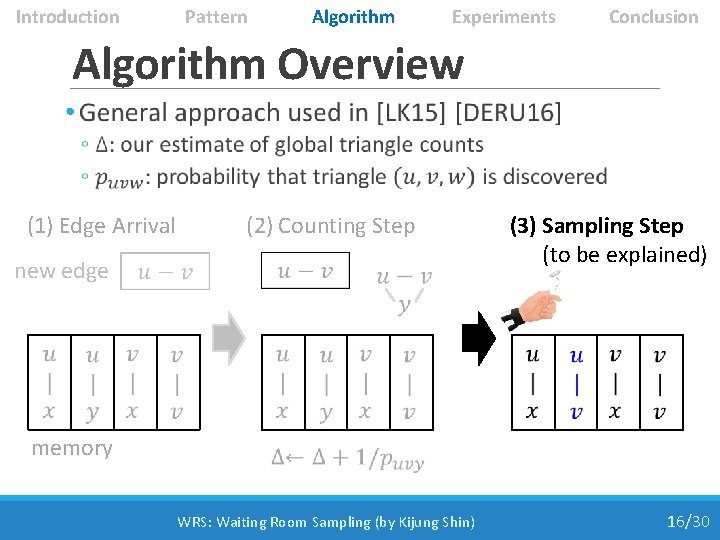
Introduction Pattern Algorithm Experiments Conclusion Algorithm Overview • WRS: Waiting Room Sampling (by Kijung Shin) 12/30

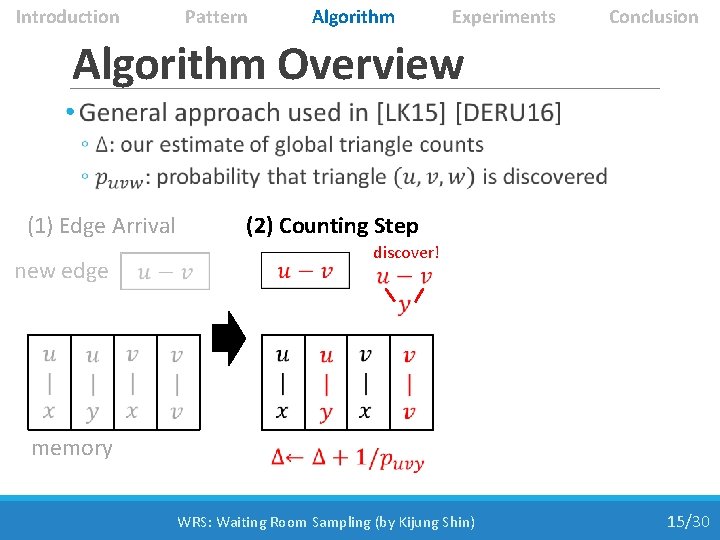
Introduction Pattern Algorithm Experiments Conclusion Algorithm Overview • (1) Edge Arrival new edge memory WRS: Waiting Room Sampling (by Kijung Shin) 13/30

Introduction Pattern Algorithm Experiments Conclusion Algorithm Overview • (1) Edge Arrival new edge memory discover! (2) Counting Step WRS: Waiting Room Sampling (by Kijung Shin) 14/30

Introduction Pattern Algorithm Experiments Conclusion Algorithm Overview • (1) Edge Arrival new edge memory discover! (2) Counting Step WRS: Waiting Room Sampling (by Kijung Shin) 15/30

Introduction Pattern Algorithm Experiments Conclusion Algorithm Overview • (1) Edge Arrival new edge memory (2) Counting Step (3) Sampling Step (to be explained) WRS: Waiting Room Sampling (by Kijung Shin) 16/30

Introduction Pattern Algorithm Experiments Conclusion Bias and Variance Analyses • WRS: Waiting Room Sampling (by Kijung Shin) 17/30

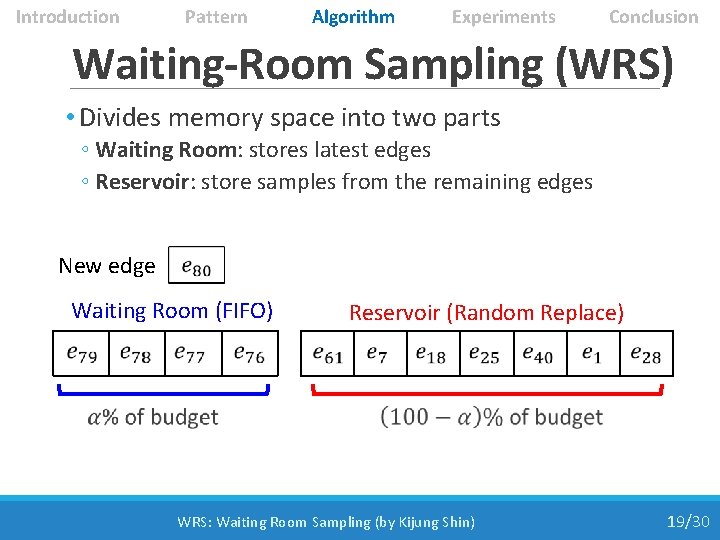
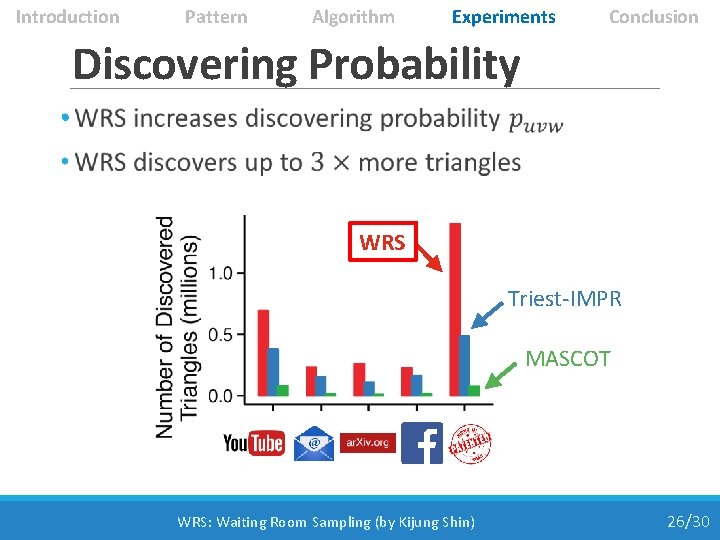
Introduction Pattern Algorithm Experiments Conclusion Increasing Discovering Prob. “How can we increase discovering probabilities of triangles? ” • Recall Temporal Locality: ◦ new edges are more likely to form ◦ triangles with recent edges ◦ than with old edges • Waiting-Room Sampling (WRS) ◦ exploits temporal locality ◦ by treating recent edges better than old edges WRS: Waiting Room Sampling (by Kijung Shin) 18/30

Introduction Pattern Algorithm Experiments Conclusion Waiting-Room Sampling (WRS) • Divides memory space into two parts ◦ Waiting Room: stores latest edges ◦ Reservoir: store samples from the remaining edges New edge Waiting Room (FIFO) Reservoir (Random Replace) WRS: Waiting Room Sampling (by Kijung Shin) 19/30

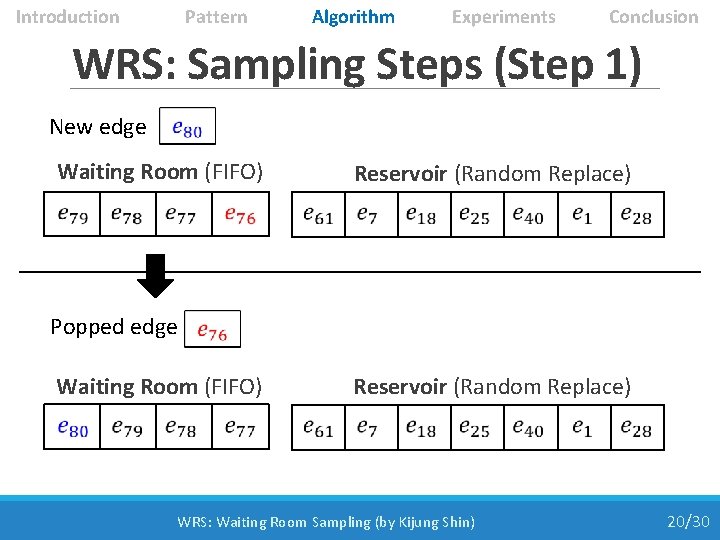
Introduction Pattern Algorithm Experiments Conclusion WRS: Sampling Steps (Step 1) New edge Waiting Room (FIFO) Reservoir (Random Replace) Popped edge Waiting Room (FIFO) Reservoir (Random Replace) WRS: Waiting Room Sampling (by Kijung Shin) 20/30

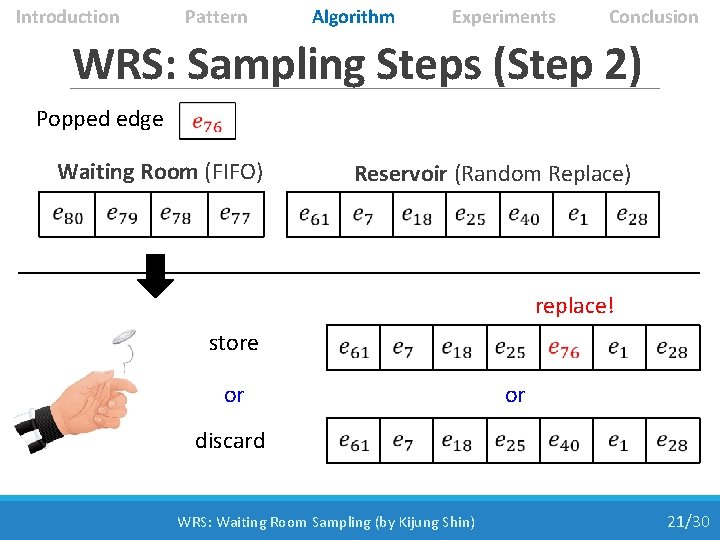
Introduction Pattern Algorithm Experiments Conclusion WRS: Sampling Steps (Step 2) Popped edge Waiting Room (FIFO) Reservoir (Random Replace) replace! store or discard or WRS: Waiting Room Sampling (by Kijung Shin) 21/30

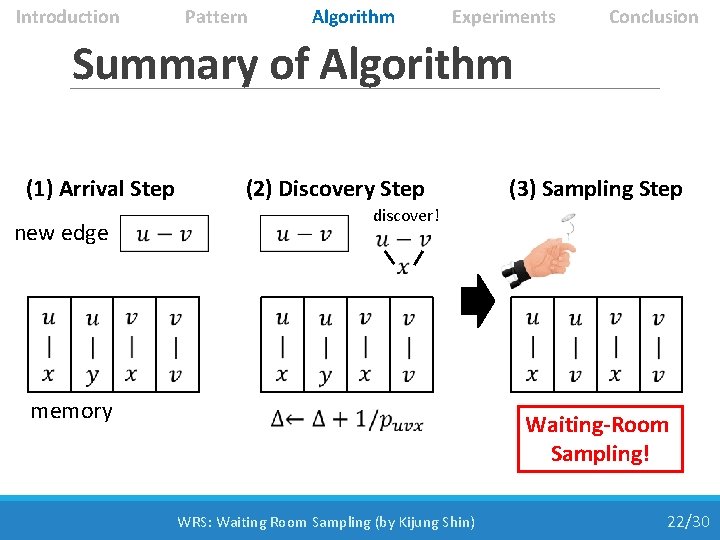
Introduction Pattern Algorithm Experiments Conclusion Summary of Algorithm (1) Arrival Step new edge memory (3) Sampling Step discover! (2) Discovery Step WRS: Waiting Room Sampling (by Kijung Shin) Waiting-Room Sampling! 22/30

Roadmap • Introduction • Temporal Pattern • Proposed Algorithm • Experiments << • Conclusion WRS: Waiting Room Sampling (by Kijung Shin) 23/30

Introduction Pattern Algorithm Experiments Conclusion Experimental Settings • citation email WRS: Waiting Room Sampling (by Kijung Shin) friendship 24/30

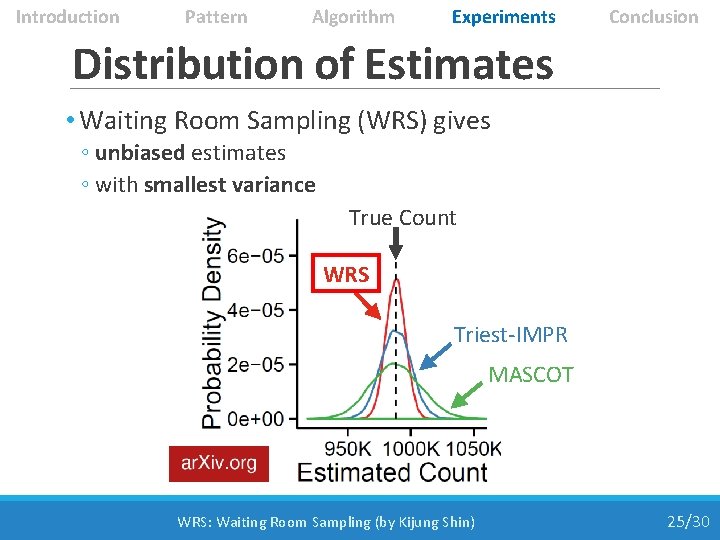
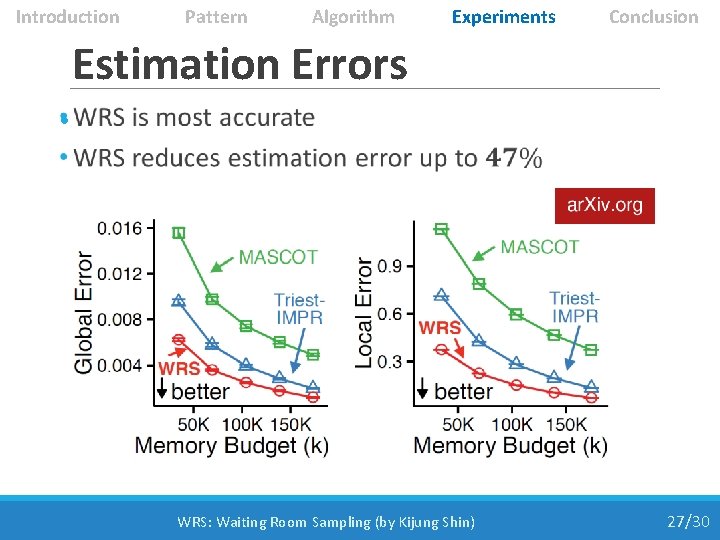
Introduction Pattern Algorithm Experiments Conclusion Distribution of Estimates • Waiting Room Sampling (WRS) gives ◦ unbiased estimates ◦ with smallest variance True Count WRS Triest-IMPR MASCOT WRS: Waiting Room Sampling (by Kijung Shin) 25/30

Introduction Pattern Algorithm Experiments Conclusion Discovering Probability • WRS Triest-IMPR MASCOT WRS: Waiting Room Sampling (by Kijung Shin) 26/30

Introduction Pattern Algorithm Experiments Conclusion Estimation Errors • WRS: Waiting Room Sampling (by Kijung Shin) 27/30

Roadmap • Introduction • Temporal Pattern • Proposed Algorithm • Experiments • Conclusion << WRS: Waiting Room Sampling (by Kijung Shin) 28/30

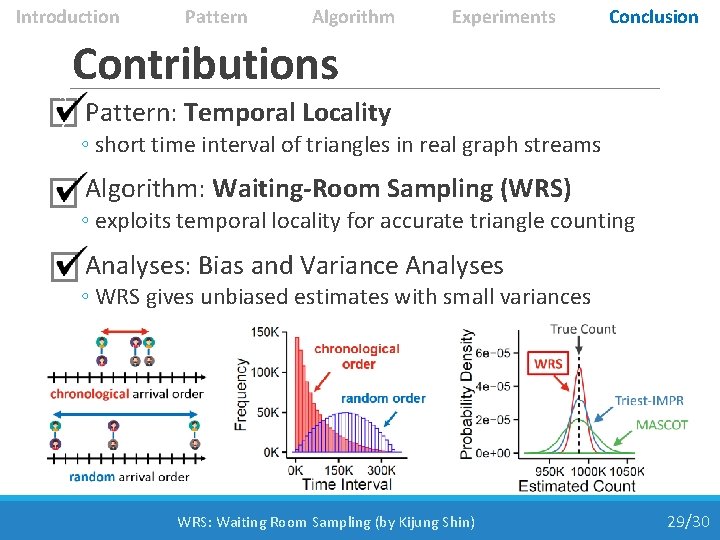
Introduction Pattern Algorithm Experiments Conclusion Contributions 0. 3 7 • Pattern: Temporal Locality ◦ short time interval of triangles in real graph streams • Algorithm: Waiting-Room Sampling (WRS) ◦ exploits temporal locality for accurate triangle counting 0 • Analyses: Bias and Variance Analyses ◦ WRS gives unbiased estimates with small variances WRS: Waiting Room Sampling (by Kijung Shin) 29/30

Thank you! • Code and datasets: ◦ https: //github. com/kijungs/waiting_room • References: ◦ [LK 15] Yongsub Lim, and U Kang. "Mascot: Memory-efficient and accurate sampling for counting local triangles in graph streams. “ KDD 2015 ◦ [DERU 16] Lorenzo De Stefani, Alessandro Epasto, Matteo Riondato and Eli Upfal. "TRIÈST: Counting Local and Global Triangles in Fully-Dynamic Streams with Fixed Memory Size. " KDD 2016 WRS: Waiting Room Sampling (by Kijung Shin) 30/30