WRITING EXPONENTIAL GROWTH MODELS A quantity is growing

Finding the Balance in an Account COMPOUND INTEREST You deposit $500 in an account

Writing an Exponential Growth Model A population of 20 rabbits is released into a

GRAPHING EXPONENTIAL GROWTH MODELS A Model with a Large Growth Factor Graph the growth

WRITING EXPONENTIAL DECAY MODELS A quantity is decreasing exponentially if it decreases by the

Writing an Exponential Decay Model From 1982 through 1997, the purchasing power of a

GRAPHING EXPONENTIAL DECAY MODELS Graphing the Decay of Purchasing Power Graph the exponential decay

GRAPHING EXPONENTIAL DECAY MODELS CONCEPT EXPONENTIAL GROWTH AND DECAY MODELS SUMMARY EXPONENTIAL GROWTH MODEL

Slides: 11

Download presentation

WRITING EXPONENTIAL GROWTH MODELS A quantity is growing exponentially if it increases by the same percent in each time period. EXPONENTIAL GROWTH MODEL C is the initial amount. t is the time period. y = C (1 + r)t (1 + r) is the growth factor, r is the growth rate. The percent of increase is 100 r.

Finding the Balance in an Account COMPOUND INTEREST You deposit $500 in an account that pays 8% annual interest compounded yearly. What is the account balance after 6 years? SOLUTION METHOD 1 SOLVE A SIMPLER PROBLEM Find the account balance A 1 after 1 year and multiply by the growth factor to find the balance for each of the following years. The growth rate is 0. 08, so the growth factor is 1 + 0. 08 = 1. 08. A 1 = 500(1. 08) = 540 Balance after one year A 2 = 500(1. 08) = 583. 20 Balance after two years A 3 = 500(1. 08)(1. 08) = 629. 856 Balance after three years A 6 = Balance after six years • • • 500(1. 08) 6 793. 437 • • •

Finding the Balance in an Account COMPOUND INTEREST You deposit $500 in an account that pays 8% annual interest compounded yearly. What is the account balance after 6 years? SOLUTION METHOD 2 USE A FORMULA Use the exponential growth model to find the account balance A. The growth rate is 0. 08. The initial value is 500. EXPONENTIAL GROWTH MODEL is the initial amount. C 500 is the initial amount. 6 tisisthe period. thetime period. A 6 y==500 C (1 (1++0. 08) r)t 6 (1(1++0. 08) thegrowth factor, 0. 08 is the growthrate. r) isisthe r is the growth 6 793. 437 The)percent of increase is 100 r. A 6 = 500(1. 08 Balance after 6 years

Writing an Exponential Growth Model A population of 20 rabbits is released into a wildlife region. The population triples each year for 5 years.

Writing an Exponential Growth Model A population of 20 rabbits is released into a wildlife region. The population triples each year for 5 years. a. What is the percent of increase each year? SOLUTION The population triples each year, so the growth factor is 3. 1+r = 3 So, the growth rate r is 2 and the percent of increase each year is 200%. Reminder: percent increase is 100 r.

Writing an Exponential Growth Model A population of 20 rabbits is released into a wildlife region. The population triples each year for 5 years. b. What is the population after 5 years? SOLUTION After 5 years, the population is P = C(1 + r) t Exponential growth model = 20(1 + 2) 5 Substitute C, r, and t. = 20 • 3 5 Simplify. = 4860 Evaluate. There will be about 4860 rabbits after 5 years. Help

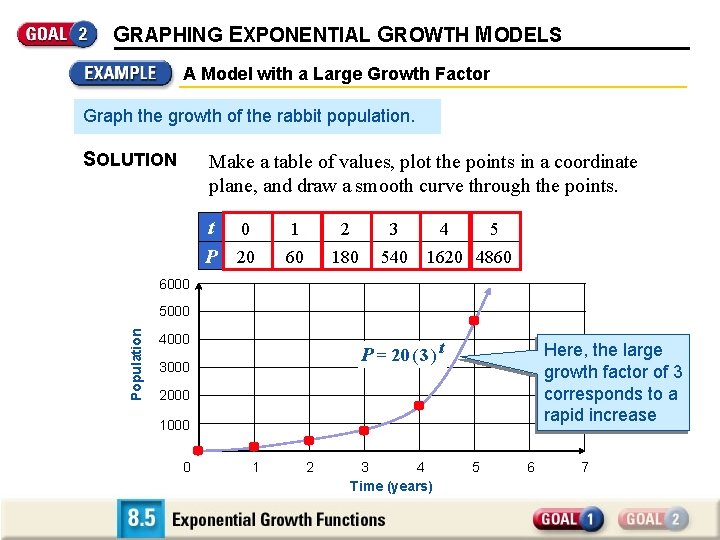
GRAPHING EXPONENTIAL GROWTH MODELS A Model with a Large Growth Factor Graph the growth of the rabbit population. SOLUTION Make a table of values, plot the points in a coordinate plane, and draw a smooth curve through the points. t 0 P 20 1 2 3 60 180 540 4 5 1620 4860 6000 Population 5000 4000 P = 20 ( 3 ) t 3000 Here, the large growth factor of 3 corresponds to a rapid increase 2000 1000 0 1 2 3 4 Time (years) 5 6 7

WRITING EXPONENTIAL DECAY MODELS A quantity is decreasing exponentially if it decreases by the same percent in each time period. EXPONENTIAL DECAY MODEL C is the initial amount. t is the time period. y = C (1 – r)t (1 – r ) is the decay factor, r is the decay rate. The percent of decrease is 100 r.

Writing an Exponential Decay Model From 1982 through 1997, the purchasing power of a dollar decreased by about 3. 5% per year. Using 1982 as the base for comparison, what was the purchasing power of a dollar in 1997? COMPOUND INTEREST SOLUTION Let y represent the purchasing power and let t = 0 represent the year 1982. The initial amount is $1. Use an exponential decay model. y = C (1 – r) t Exponential decay model = (1)(1 – 0. 035) t Substitute 1 for C, 0. 035 for r. = 0. 965 t Simplify. Because 1997 is 15 years after 1982, substitute 15 for t. y = 0. 96515 Substitute 15 for t. 0. 59 The purchasing power of a dollar in 1997 compared to 1982 was $0. 59.

GRAPHING EXPONENTIAL DECAY MODELS Graphing the Decay of Purchasing Power Graph the exponential decay model in the previous example. Use the graph to estimate the value of a dollar in ten years. SOLUTION Help Make a table of values, plot the points in a coordinate plane, and draw a smooth curve through the points. t 0 1 2 3 4 5 6 7 8 9 10 y 1. 00 0. 965 0. 931 0. 899 0. 867 0. 837 0. 808 0. 779 0. 752 0. 726 0. 7 y = 0. 965 t 0. 8 (dollars) Purchasing Power 1. 0 0. 6 0. 4 0. 2 0 1 2 3 Your dollar of today will be worth about 70 cents in ten years. 4 5 6 7 8 Years From Now 9 10 11 12

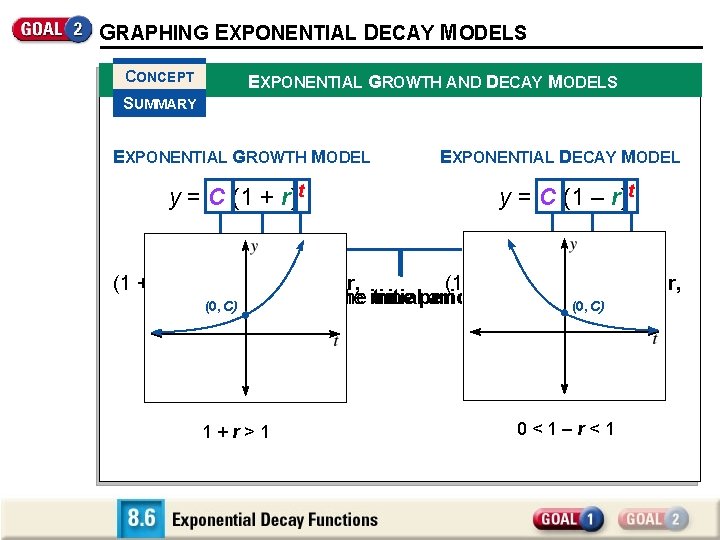
GRAPHING EXPONENTIAL DECAY MODELS CONCEPT EXPONENTIAL GROWTH AND DECAY MODELS SUMMARY EXPONENTIAL GROWTH MODEL y = C (1 + r)t EXPONENTIAL DECAY MODEL y = C (1 – r)t An exponential model y = a • b t represents exponential growth b > 1 and exponential(1 decay 0 <decay b < 1. factor, (1 + r) is theifgrowth factor, – r) isifthe Ct is is the initial time period. amount. C) (0, C) rate. r is the(0, growth rate. r is the decay 1+r>1 0<1–r<1