Writing Equations for Word Problems A Problem Solving

Writing Equations for Word Problems

A Problem Solving Plan Using Models Step 1 READ the problem very carefully. Step 2 LABEL the unknown by writing a “LET STATEMENT”. Step 3 Write a VERBAL MODEL that represents the logical set up of the problem. Step 4 Write the ALGEBRAIC MODEL. The Algebraic Model is the same as the equation that represents the Verbal Model.

Todd is five years older than Ben. The sum of their ages is 35. Find both of their ages. Step 1 READ the problem very carefully. Decide what is asked for and what information is given. If you need to, make a sketch. You are asked to find their ages when only the sum is given.

Todd is five years older than Ben. The sum of their ages is 35. Find both of their ages. Step 2 LABEL one unknown number by writing a “Let Statement”. Choose a variable appropriate to the problem. How do you know which person should represent the variable? A good rule of thumb is to let the variable represent whomever they give the least information about in the problem. Another good tip is to let the variable represent the answer you are looking for. let b = Ben's age Then write all other unknown numbers in terms of the let b + 5 = Todd's age variable already used. In these problems you may NOT use more than one variable You may not have variable “t ” and a variable “b”.

Todd is five years older than Ben. The sum of their ages is 35. Find both of their ages. Step 3 Write a VERBAL MODEL that represents the logical set up of the problem. Ben's age + Todd's age = Total ages Whenever you see that you have a total your verbal model will almost always be one thing added to the other is equal to the total. Verbal models are written with WORDS not numbers or variables. Step 4 Write the ALGEBRAIC MODEL. The Algebraic Model is the same as the equation that represents the Verbal Model. Write the equation by substituting your “let statements" into your Verbal Model. This is "Translating" the Verbal Model into an equation.

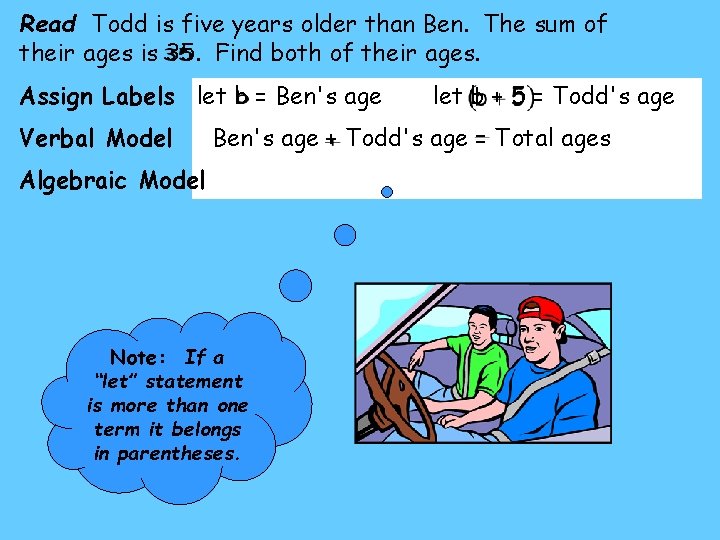
Read Todd is five years older than Ben. The sum of their ages is 35. Find both of their ages. Assign Labels let b = Ben's age Verbal Model let b + 5 = Todd's age Ben's age + Todd's age = Total ages Algebraic Model Note: If a “let” statement is more than one term it belongs in parentheses.

Example 1 In a game, Ben’s score was 3 times Sam’s score. Together they scored 80 points. Find their scores. Assign Labels. let s = Sam’s score let 3 s = Ben’s score Verbal Model. Sam’s score + Ben’s score == total Algebraic Model.

Example 2 Meg’s age is 5 times Jose’s age. The sum of 18 How old is each? their ages is 18. Let j = Jose’s age Let 5 j 5 j = Meg’s age Assign Labels. Verbal Model. Algebraic Model. Jose’s age + Meg’s age = Total

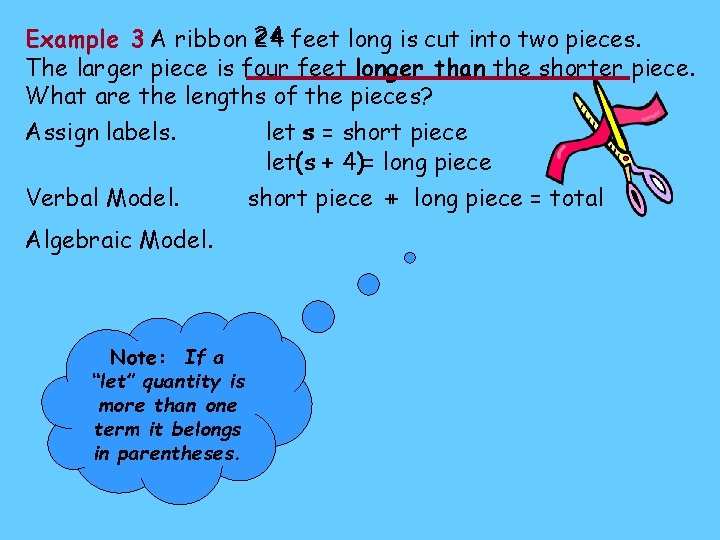
Example 3 A ribbon 24 feet long is cut into two pieces. The larger piece is four feet longer than the shorter piece. What are the lengths of the pieces? Assign labels. let s = short piece let(s s+4 4)= long piece Verbal Model. short piece ++ long piece = total Algebraic Model. Note: If a “let” quantity is more than one term it belongs in parentheses.

Example 4 Together Gini and Jo. Ann own 87 pairs of shoes. Jo. Ann has 25 more pairs than Gini has. How many pairs does Gini have? 25)= Jo. Ann’s Let g = Gini’s + Let (g g ++ 25 Assign Labels. shoes Verbal Model. Gini’s shoes + Jo. Ann’s shoes = Total = Algebraic Model. Note: If a “let” statement is more than one term it belongs in parentheses.