WP 31 Effects of Rounding on Data Quality



![B : Base : Quotient : Remainder Types of rounding: • Unbiased rounding: E[R(r)|r] B : Base : Quotient : Remainder Types of rounding: • Unbiased rounding: E[R(r)|r]](https://slidetodoc.com/presentation_image_h2/06254c0ae27cb479e0fbfff37ff91e30/image-4.jpg)



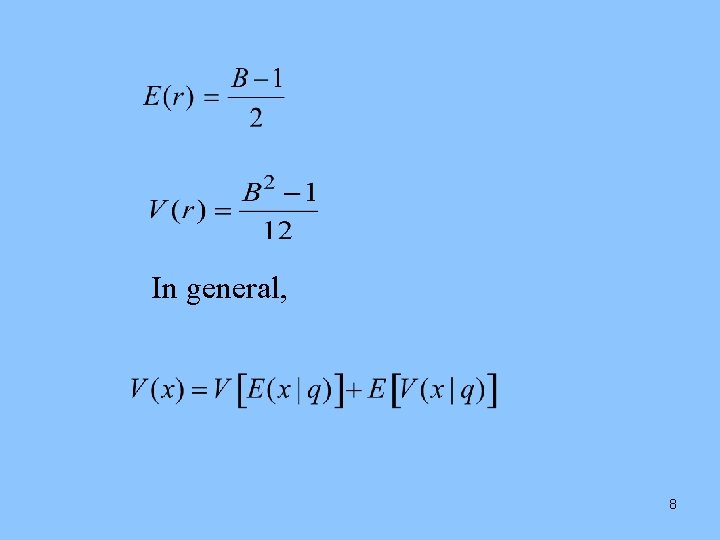




















- Slides: 28

WP. 31 Effects of Rounding on Data Quality Jay J. Kim , Lawrence H. Cox, Myron Katzoff, Joe Fred Gonzalez, Jr. U. S. National Center for Health Statistics 1

I. Introduction Reasons for rounding • Rounding noninteger values to integer values for statistical purposes; • To enhance readability of the data; • To protect confidentiality of records in the file; • To keep the important digits only. 2

• Purpose: Evaluate the effects of four rounding methods on data quality and utility in two ways: • (1) bias and variance; • (2) effects on the underlying distribution of the data determined by a distance measure. 3
![B Base Quotient Remainder Types of rounding Unbiased rounding ERrr B : Base : Quotient : Remainder Types of rounding: • Unbiased rounding: E[R(r)|r]](https://slidetodoc.com/presentation_image_h2/06254c0ae27cb479e0fbfff37ff91e30/image-4.jpg)
B : Base : Quotient : Remainder Types of rounding: • Unbiased rounding: E[R(r)|r] = r • Sum-unbiased rounding: E[R(r)] = E(r) 4

II. Four rounding rules 1. Conventional rounding Suppose r = 0, 1, 2, . . . , 9 (=B-1). If r (B/2), round r up to 10 (=B) else round down r to zero (0). If B is odd, round r up when r 5

r is assumed to follow a discrete uniform distribution 2. Modified Conventional rounding Same as conventional rounding, except rounding 5 (B/2) up or down with probability ½. 3. Zero-restricted 50/50 rounding Except zero (0), round r up or down with probability ½. 6

4. Unbiased rounding rule Round r up with probability r/B Round r down with probability 1 - r/B III. Mean and variance III. 1 Mean and variance of unrounded number r = 0, 1, 2, 3, . . . B-1. 7
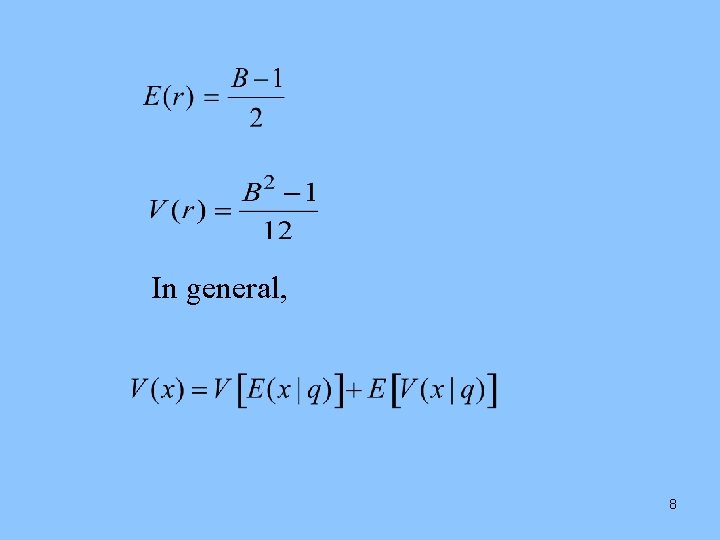
In general, 8

III. 2 Conventional rounding when B is even for unrounded number. 9

10

III. 3 Conventional rounding when B is odd for unrounded number 11

Modified conventional rounding, 50/50 rounding and unbiased rounding have the same mean, variance and MSE as the conventional rounding with odd B. 12

IV. Distance measure Define 13

Reexpressing the numerator of U, we have With conventional rounding with B=10, Then we have 14

Expected value of U We define 15

IV. 1 Conventional rounding with even B which can be reexpressed as 16

The upper and lower bounds for harmonic series are The upper bound for the first term of 17

The second term of Note the second term of E(U) is, IV. 2 Modified conventional rounding with even B Has the same E(U) as the conventional rounding. 18

IV. 3 50/50 rounding The first term of The second term IV. 4 Unbiased rounding The first term of 19

The second term: IV. 5 Comparisons of three rounding rules Conv 50/50 Unbiased 1 st Term 2 nd Term 20

Comparisons of three rounding rules B=10 Conv 50/50 1 st term 2. 61 11. 49 (4. 4) 2 nd term . 85 2. 85 Unbiased 4. 5 (1. 7) 1. 65 21

Comparisons of three rounding rules B=1, 000 Conv 1 st term 193. 65 2 nd term 83. 33 50/50 Unbiased 3, 453. 88 (18) 499. 5 (2. 6) 322. 83 166. 67 22

IV. 6 E(1/q) for log-normal distribution Let y = ln x Then, x has a lognormal distribution, i. e. , 23

Let Then IV. 6 E(1/q) for Pareto distribution of 2 nd kind The Pareto distribution of the second kind is, 24

where k is the minimum value of q and c is the cumulative probability from 1. IV. 7 Upper limit for E(1/q) for multinomial distribution The multinomial distribution has the form = 0, 1, 2, 25

Note, for all i. Let be the size of the category i and 26

V. Concluding comments Various methods of rounding and in some applications various choices for rounding base B are available. The question becomes: which method and/or base is expected to perform best in terms of data quality and preserving distributional properties of original data and, quantitatively, what is the expected distortion due to rounding? This paper provides a preliminary analysis toward answering these questions 27

References Grab, E. L & Savage, I. R. (1954), Tables of the Expected Value of 1/X for Positive Bernoulli and Poisson Variables, Journal of the American Statistical Association 49, 169177. N. L. Johnson & S. Kotz (1969). Distributions in Statistics, Discrete Distributions, Boston: Houghton Mifflin Company. N. L. Johnson & S. Kotz (1970). Distributions in Statistics, Continuous Univariate Distributions-1, New York: John Wiley and Sons, Inc. Kim, Jay J. , Cox, L. H. , Gonzalez, J. F. & Katzoff, M. J. (2004), Effects of Rounding Continuous Data Using Rounding Rules, Proceedings of the American Statistical Association, Survey Research Methods Section, Alexandria, VA, 3803 -3807 (available on CD). Vasek Chvatal. Harmonic Numbers, Natural Logarithm and the Euler-Mascheroni Constant. See www. cs. rutgers. edu/~chvatal/notes/harmonic. html 28