WORM ALGORITHM FOR CLASSICAL AND QUANTUM STATISTICAL MODELS

WORM ALGORITHM FOR CLASSICAL AND QUANTUM STATISTICAL MODELS Nikolay Prokofiev, Umass, Amherst Many thanks to collaborators on major algorithm developments Boris Svistunov, Umass, Amherst Igor Tupitsyn, PITP Vladimir Kashurnikov, MEPI, Moscow Evgeni Burovski, Umass, Amherst Massimo Boninsegni, UAlberta, Edmonton NASA Les Houches, June 2006

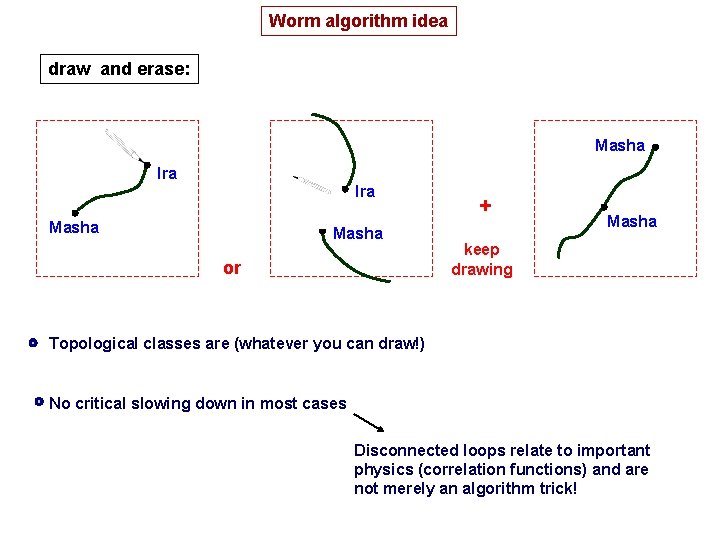
Worm algorithm idea Consider: - configuration space = arbitrary closed loops - each cnf. has a weight factor - quantity of interest

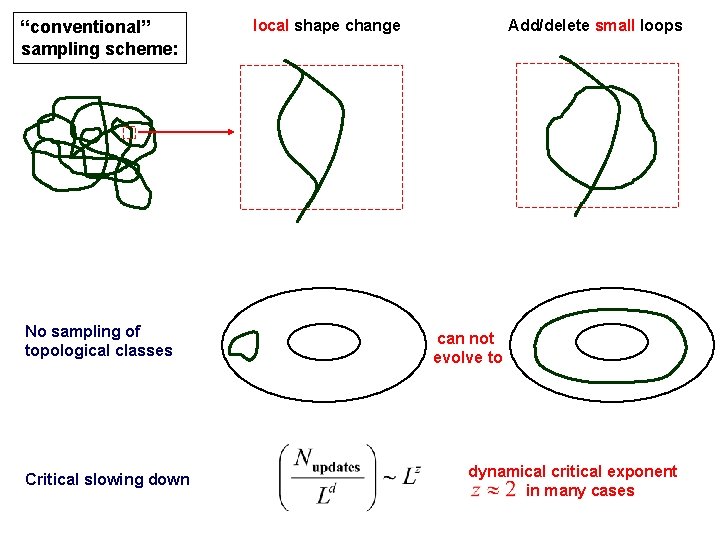
“conventional” sampling scheme: No sampling of topological classes Critical slowing down local shape change Add/delete small loops can not evolve to dynamical critical exponent in many cases

Worm algorithm idea draw and erase: Masha Ira Masha or + Masha keep drawing Topological classes are (whatever you can draw!) No critical slowing down in most cases Disconnected loops relate to important physics (correlation functions) and are not merely an algorithm trick!

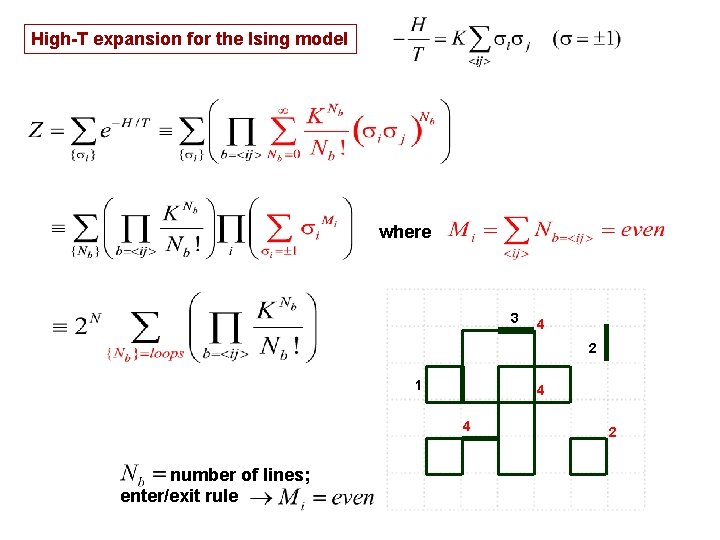
High-T expansion for the Ising model where 3 4 2 1 4 4 number of lines; enter/exit rule 2

Spin-spin correlation function: Worm algorithm cnf. space = I Same as for generalized partition 1 3 4 M 4 2

Getting more practical: since Complete algorithm: - If , select a new site for - select direction to move - If accept at random , let it be bond with prob.

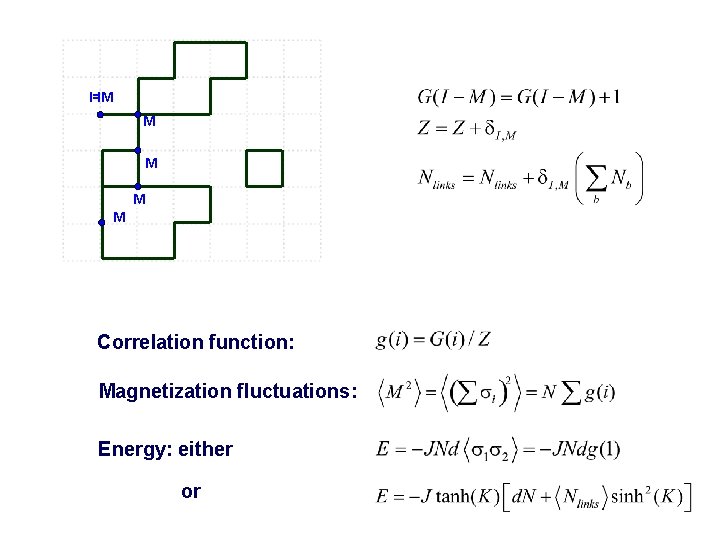
I=M I M M Correlation function: Magnetization fluctuations: Energy: either or

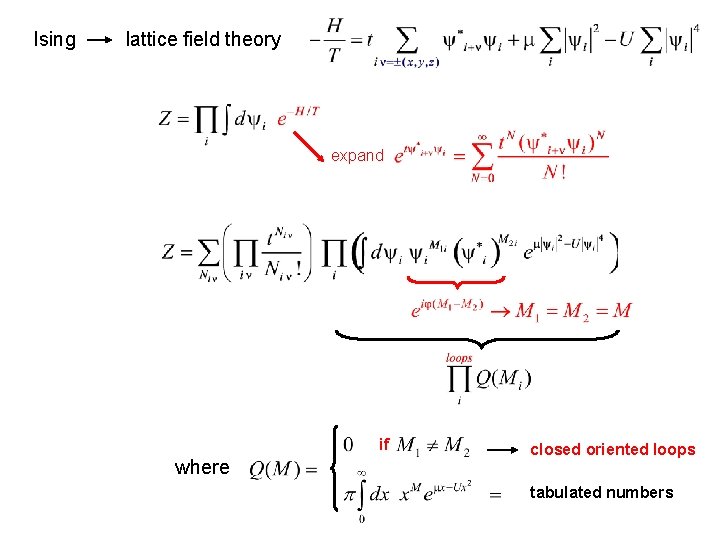
Ising lattice field theory expand if where closed oriented loops tabulated numbers

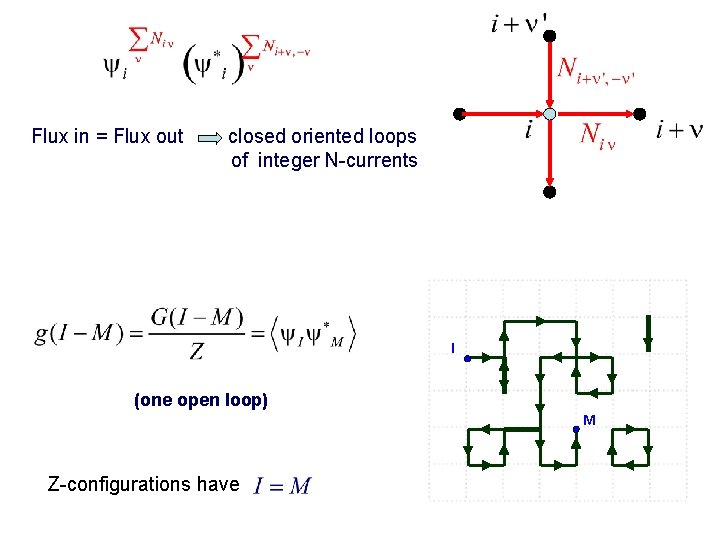
Flux in = Flux out closed oriented loops of integer N-currents I (one open loop) M Z-configurations have

Same algorithm: I=M sectors, prob. to accept M M draw erase Keep drawing/erasing … M M

Multi-component gauge field-theory (deconfined criticality, XY-VBS and Neel-VBS quantum phase transitions… XY-VBS transition; understood (? ) no DCP, always first-order Neel-VBS transition, unknown !

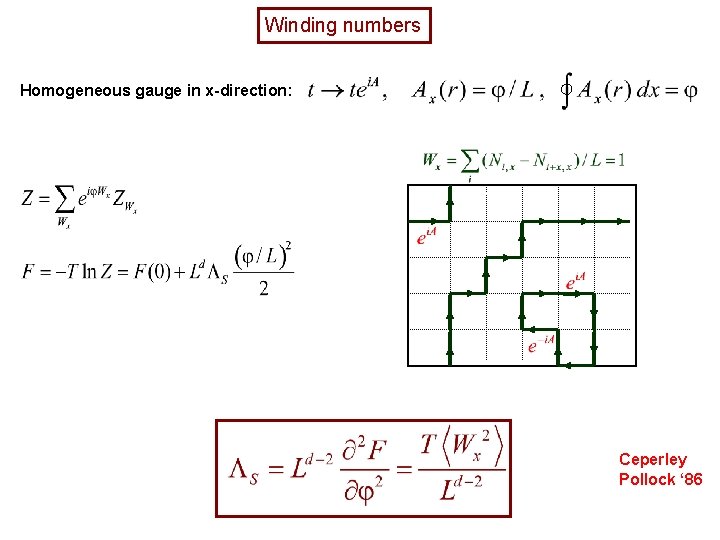
Winding numbers Homogeneous gauge in x-direction: Ceperley Pollock ‘ 86