Workshop on Probing and Understanding Exotic Superconductors and

Workshop on Probing and Understanding Exotic Superconductors and Superfluids – 30 October 2014 Mobility edge of atoms in laser speckle potentials: exact calculations Vs self-consistent approaches Giuliano Orso Laboratoire Matériaux et Phénomènes Quantiques Université Paris Diderot (Paris) Work in collaboration with: Dominique Delande LKB, ENS and Université Pierre et Marie Curie (Paris)

Outline Anderson localization with cold atoms in laser speckles Numerical computation of the mobility edge Self-consistent theory of localization On site-distribution and blue-red asymmetry Role of the spatial correlation function Comparison with experiments

Anderson localization Particle in a disordered (random) potential: One-dimensional system Two-dimensional system Particle with energy E Disordered potential V(z) (typical value V 0) When , the particle is classically trapped in the potential wells. When , the classical motion is ballistic in 1 d, typically diffusive in dimension 2 and higher. Quantum interference of scattering paths may inhibit diffusion at long times => • Anderson localization

Anderson localization • Halt of diffusion due to exponential localization of single-particle states Low disorder “deformed” Bloch state strong disorder localization length • difficult to see with electrons in disordered solids (due to e-e interactions and phonon scattering) ⇒ ULTRA-COLD ATOMS? • easier to observe with classical waves: microwaves, light, acoustic waves, seismic waves, etc.

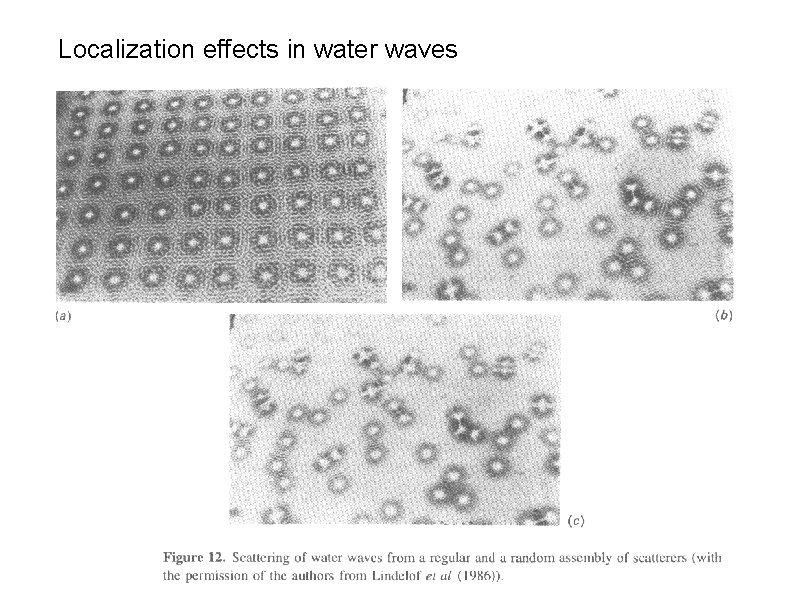
Localization effects in water waves

Anderson localization with cold atoms Orders of magnitude: Very favorable! Velocity: cm/s De Broglie wavelength: mm Time: ms-ms ⇒can directly observe the expansion of wave-packet Interaction effects can be reduced or cancelled (use Feshbach resonances or very dilute samples), no phonon scattering ⇒density profile = (atomic wave-function)2 A tunable disorder is added using light-atom interaction: - quasi-periodic potentials (1 dimension, Aubry-André model) G. Modugno (Florence) - speckle patterns (any dimension) A. Aspect (Palaiseau), B. De. MArco (Urbana-C), G. Modugno

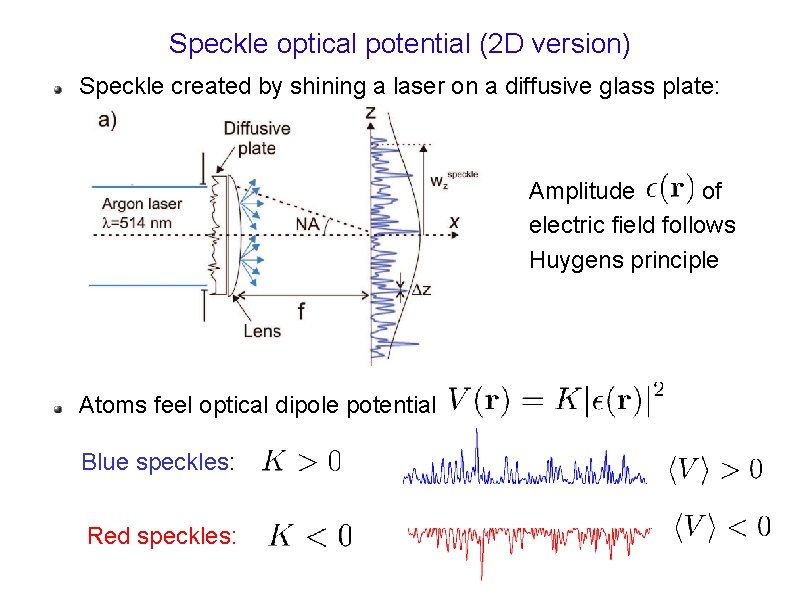
Speckle optical potential (2 D version) Speckle created by shining a laser on a diffusive glass plate: Amplitude of electric field follows Huygens principle Atoms feel optical dipole potential Blue speckles: Red speckles:

1) On-site potential distribution P(V) for speckles From central limit theorem, real and imaginary parts of field amplitude are independent gaussian random variables Disorder potential is modulo square of field amplitude ⇒P(V) is not gaussian but exponential: : Step function

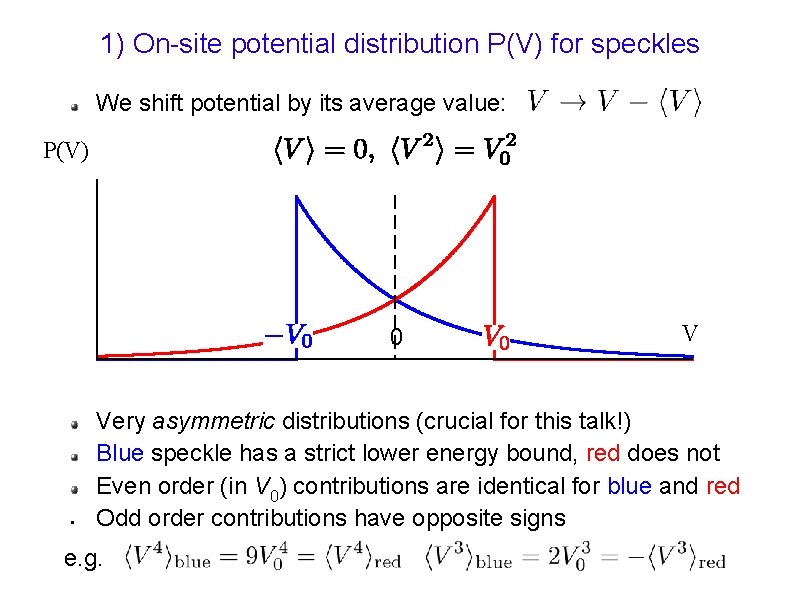
1) On-site potential distribution P(V) for speckles We shift potential by its average value: P(V) 0 • V Very asymmetric distributions (crucial for this talk!) Blue speckle has a strict lower energy bound, red does not Even order (in V 0) contributions are identical for blue and red Odd order contributions have opposite signs e. g.

A typical realization of a 2 D blue-detuned speckle potential Dark region (low potential, ocean floor, zero energy) Bright spot (high potential) Rigorous low energy bound, no high energy bound

2) Spatial correlation of speckles Correlation function for 2 D circular aperture: a : numerical aperture of the device imaging the speckle 3 D isotropic spherical speckle: Define correlation energy: correlation length σ ∼ 1μm

Two (coherent) crossed speckles 3 D speckles can be realized experimentally by crossing two orthogonal 2 D speckles. They are anisotropic in general. courtesy V. Josse

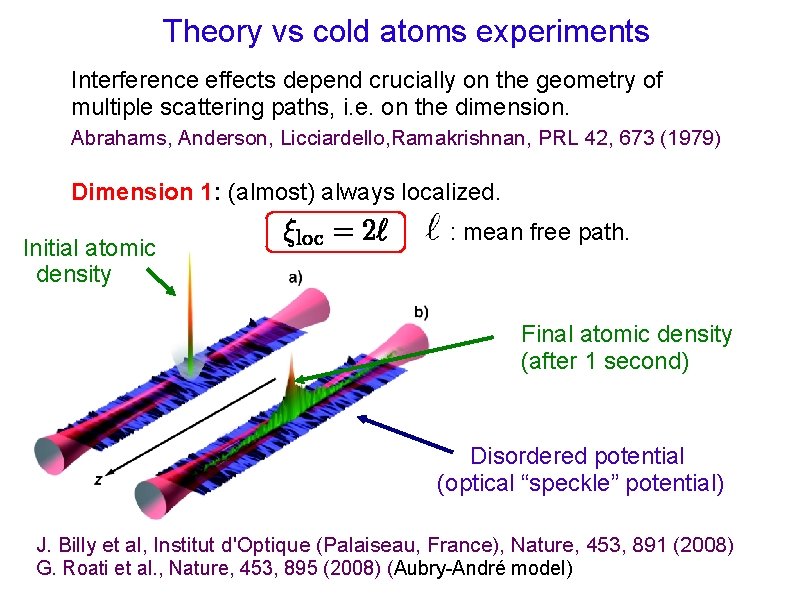
Theory vs cold atoms experiments Interference effects depend crucially on the geometry of multiple scattering paths, i. e. on the dimension. Abrahams, Anderson, Licciardello, Ramakrishnan, PRL 42, 673 (1979) Dimension 1: (almost) always localized. Initial atomic density : mean free path. Final atomic density (after 1 second) Disordered potential (optical “speckle” potential) J. Billy et al, Institut d'Optique (Palaiseau, France), Nature, 453, 891 (2008) G. Roati et al. , Nature, 453, 895 (2008) (Aubry-André model)

Theory vs cold atoms experiments Dimension 2: marginally localized. : particle wave-vector Weak localization effects (coherent backscattering) observed. Hard to observe strong (Anderson) localization: • speckles have high threshold value for classical percolation • for large k, localization length can exceed the system size!! Jendrzejewski et al, PRL 109, 195302 (2012)

Theory vs cold atoms experiments localized Dimension 3: metal-insulator transition • • Localized states near band edge Extended states in interior Mobility edges Ec separating two phases Second order phase transition at E=Ec: extended Universal critical exponent Expect (orthogonal universality class) Paris-Lille collaboration: kicked-rotor model with cold atoms 3 D Anderson transition in momentum space Test of universality exponent J. Chabé et al, PRL 101, 25 (2008) 255702

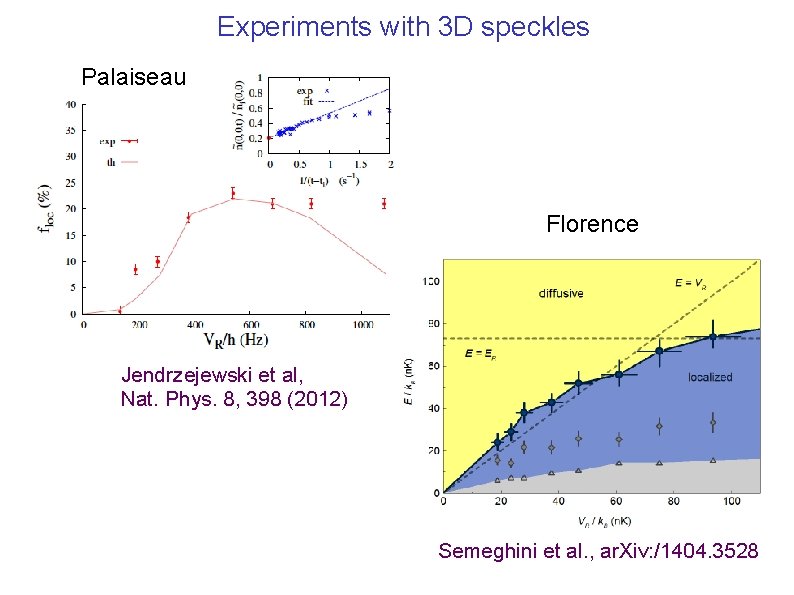
Experiments with 3 D speckles Palaiseau Florence Jendrzejewski et al, Nat. Phys. 8, 398 (2012) Semeghini et al. , ar. Xiv: /1404. 3528

Hard to locate the mobility edge experimentally: 1) broad energy distribution of atoms; initial wave-packet contains both localized and extended states. So only a fraction of atoms actually localizes! 2) Comparison with theory is unclear ; there exist different estimates of Ec based on different implementations of Self-Consistent Theory of Localization (SCTL) Kuhn et al. , NJP 9, 161 (2007) Yedjour and Van Tiggelen, Eur. Phys. J. D 59, 249 (2010) Piraud, Pezzé, and Sanchez-Palencia, NJP 15, 075007 (2013) These theories contain several approximations and seem to contradict each other: which one should we trust?

Can we make numerically exact predictions for the mobility edge of atoms in 3 D speckles? o Non-Gaussian on-site distribution P(V) for blue/red speckles o To compare with SCTL theories assume isotropic spatial correlation: Delande and Orso, PRL 113, 060601 (2014)

Outline Anderson localization with cold atoms in laser speckles Numerical computation of the mobility edge Self-consistent theory of localization On site-distribution and blue-red asymmetry Role of the spatial correlation function Comparison with experiments

First step: Mapping problem to Anderson model Spatial discretization of the Schrödinger equation on a cubic grid of step D. : 5 -10 points per correlation length (error <1%) Speckle generated numerically on the grid Proper correlation function imprinted by an appropriate filter in Fourier space ⇒ Only states at bottom of the band are important

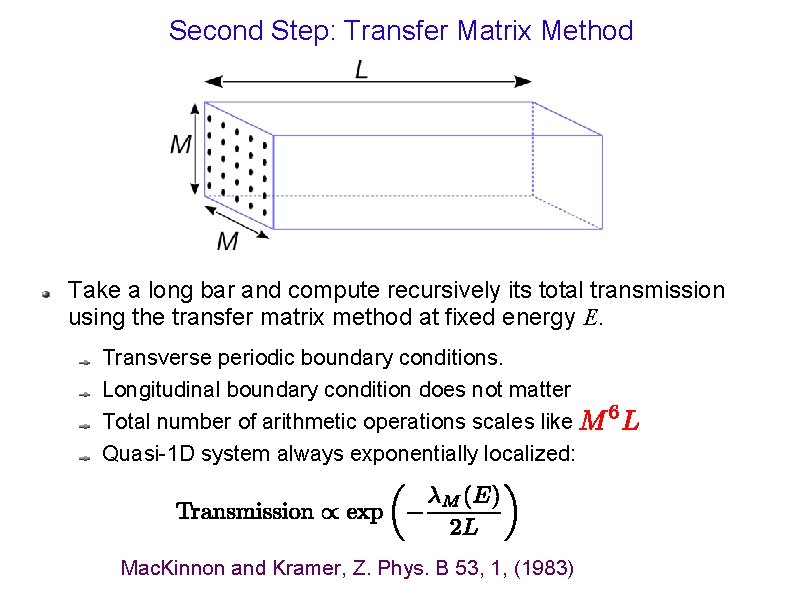
Second Step: Transfer Matrix Method Take a long bar and compute recursively its total transmission using the transfer matrix method at fixed energy E. Transverse periodic boundary conditions. Longitudinal boundary condition does not matter Total number of arithmetic operations scales like Quasi-1 D system always exponentially localized: Mac. Kinnon and Kramer, Z. Phys. B 53, 1, (1983)

Second Step: Transfer Matrix Method For a given disorder strength V 0, compute l. M(E) for various values of energy E and increasing values of M. Requires relative accuracy in the 0. 1 -1% range ⇒ 35<M<90 Speed up calculations by cutting the long bar in smaller pieces and averaging out results (eq. to disorder average) In the localized regime: x(E): true 3 D localization length In the diffusive regime, l. M(E) diverges (like M 2) for large M. At the mobility edge, l. M(E) is proportional to M. => Study vs. M and E. Fixed point is the mobility edge!

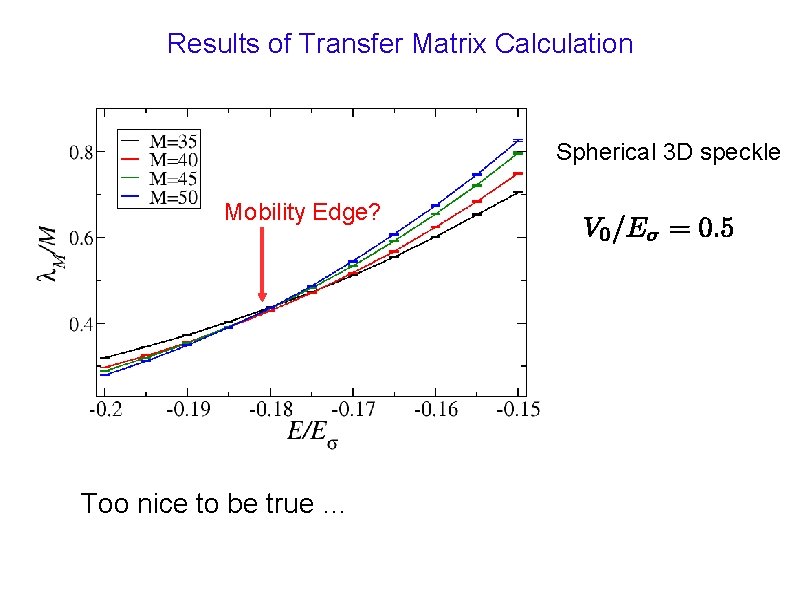
Results of Transfer Matrix Calculation Spherical 3 D speckle Mobility Edge? Too nice to be true …

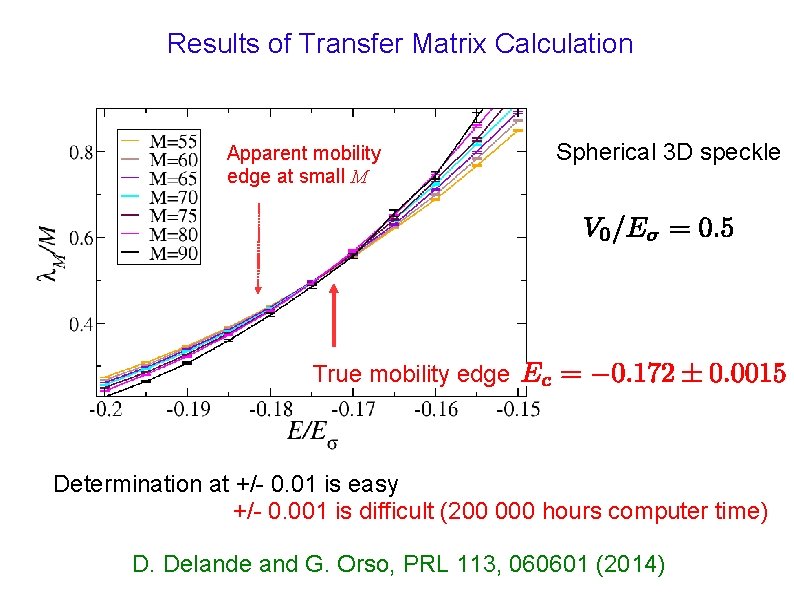
Results of Transfer Matrix Calculation Apparent mobility edge at small M Spherical 3 D speckle True mobility edge Determination at +/- 0. 01 is easy +/- 0. 001 is difficult (200 000 hours computer time) D. Delande and G. Orso, PRL 113, 060601 (2014)

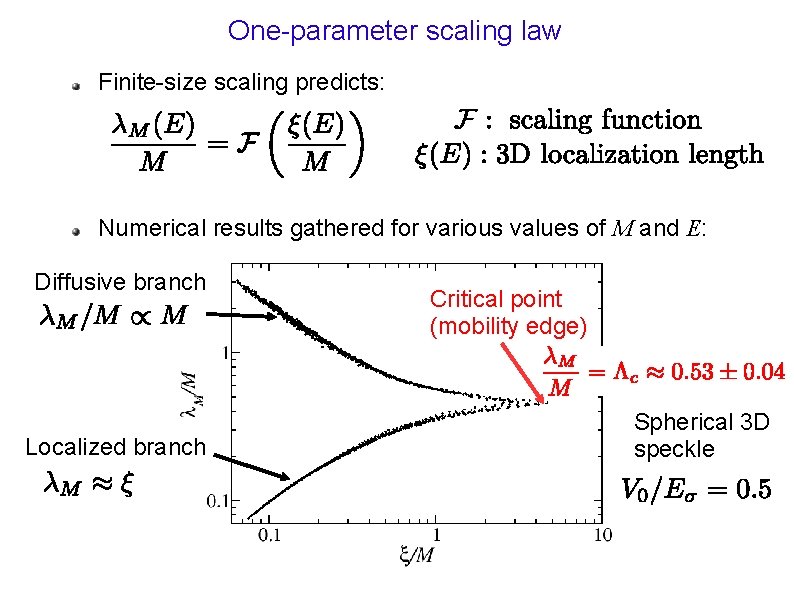
One-parameter scaling law Finite-size scaling predicts: Numerical results gathered for various values of M and E: Diffusive branch Localized branch Critical point (mobility edge) Spherical 3 D speckle

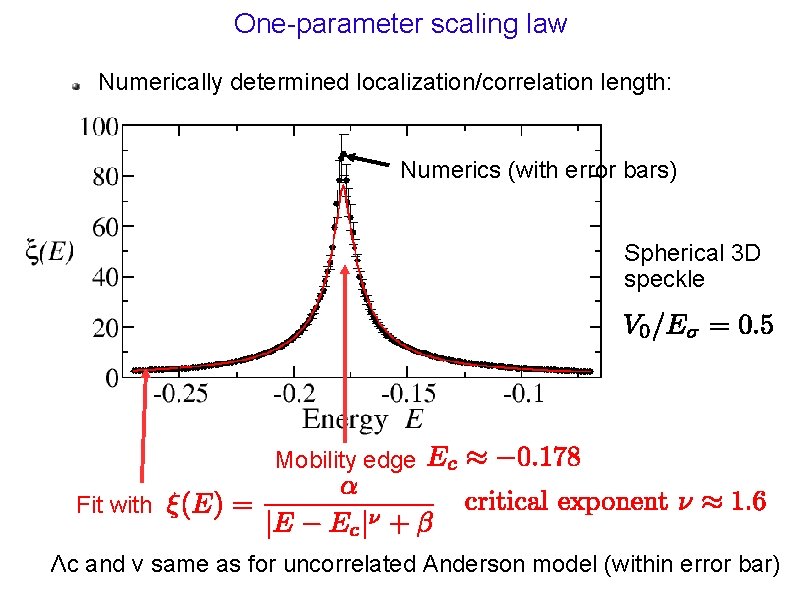
One-parameter scaling law Numerically determined localization/correlation length: Numerics (with error bars) Spherical 3 D speckle Mobility edge Fit with Λc and ν same as for uncorrelated Anderson model (within error bar)

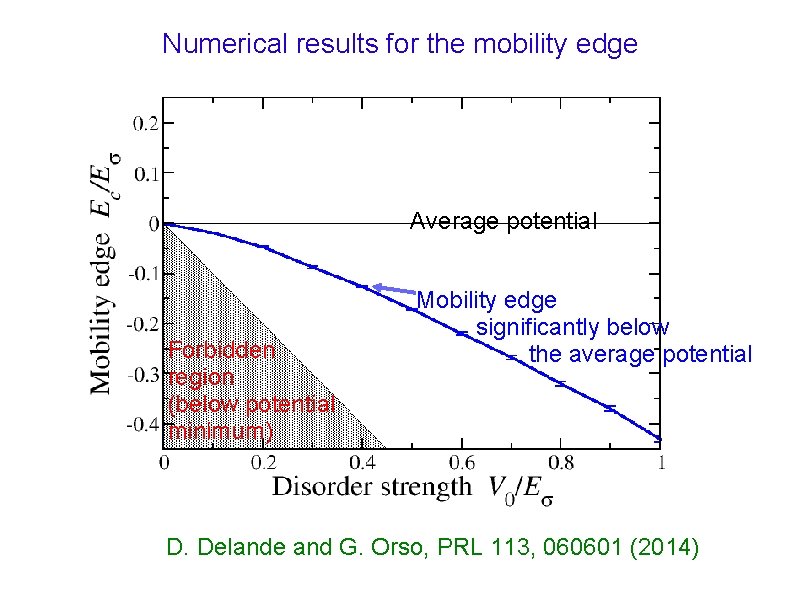
Numerical results for the mobility edge Average potential Forbidden region (below potential minimum) Mobility edge significantly below the average potential D. Delande and G. Orso, PRL 113, 060601 (2014)

Outline Anderson localization with cold atoms in laser speckles Numerical computation of the mobility edge Self-consistent theory of localization On site-distribution and blue-red asymmetry Role of the spatial correlation function Comparison with experiments

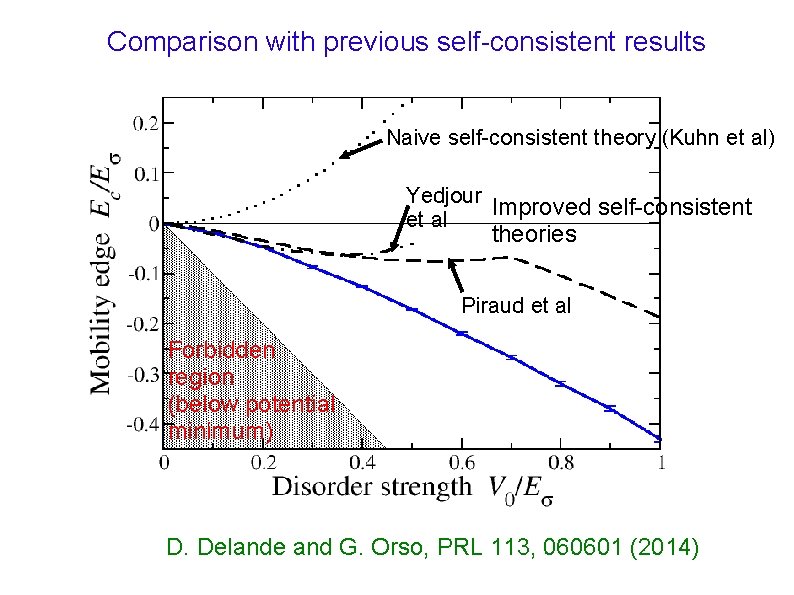
Comparison with previous self-consistent results Naive self-consistent theory (Kuhn et al) Yedjour Improved self-consistent et al theories Piraud et al Forbidden region (below potential minimum) D. Delande and G. Orso, PRL 113, 060601 (2014)

Self-consistent theory of localization Following Vollhardt and Wölfle (80's and 90's). The starting point is the weak localization correction to the diffusion constant due to closed loops: : Boltzmann diffusion constant : density of states : Diffusion constant (including interference) Self-consistent theory: The onset of localization is characterized by: at small w

Intrinsic limits of the self-consistent theory of localization: • It is by itself an approximate theory (e. g. it predits the wrong critical exponent ν=1) • it requires the knowledge of disorder-averaged Green’s function: need further approximations (e. g. Born or Selfconsistent Born approximation, CPA, etc. ) • It is based on a hydrodynamic approach; Ec value depends on UV cut-off in momentum space: Vollhardt & Wölfle, PRL 48, 699 (1982); Economou & Soukoulis, PRB 28, 1093 (1983)

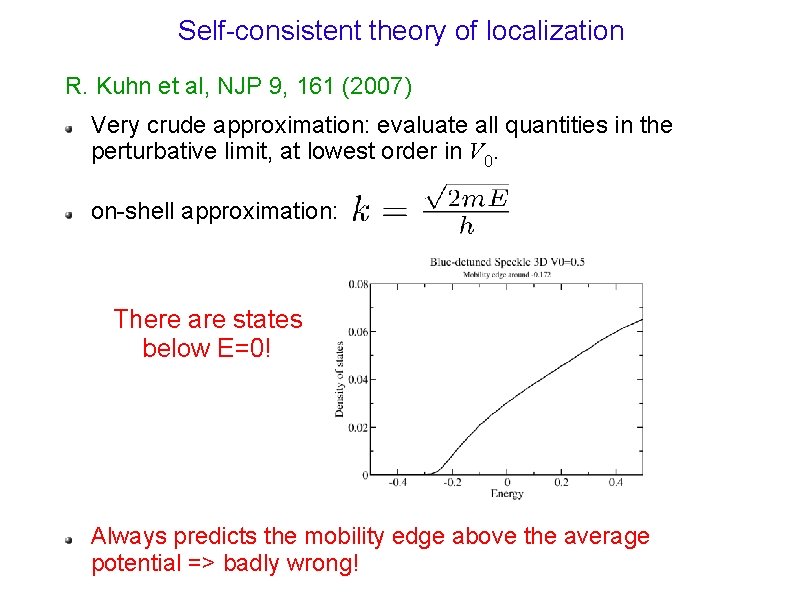
Self-consistent theory of localization R. Kuhn et al, NJP 9, 161 (2007) Very crude approximation: evaluate all quantities in the perturbative limit, at lowest order in V 0. on-shell approximation: There are states below E=0! Always predicts the mobility edge above the average potential => badly wrong!

Self-consistent theory of localization A. Yedjour and B. v. Tiggelen, EPJD 59, 249 (2010) M. Piraud, L. Pezzé and L. Sanchez-Palencia, NJP 15, 075007 (2013) Improvement: take into account the shift of the lower bound of the energy spectrum (real part of self-energy) via selfconsistent Born approximation Correctly predict that Ec is negative for blue speckle but … 1) the value of Ec is not very accurate; contributions from all order in V 0 are important! 2) They predict same value of Ec for blue and red speckles, because the calculated self-energy is the same. This is wrong.

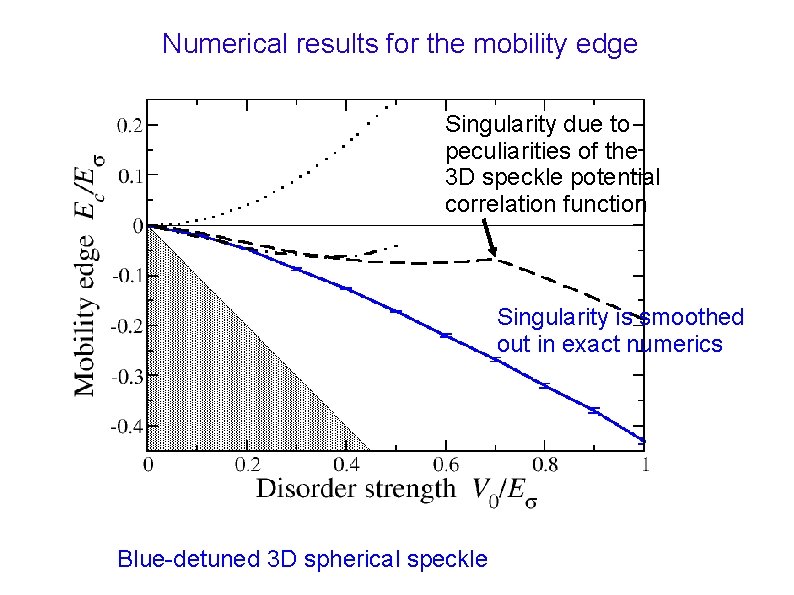
Numerical results for the mobility edge Singularity due to peculiarities of the 3 D speckle potential correlation function Singularity is smoothed out in exact numerics Blue-detuned 3 D spherical speckle

Self-consistent theory of localization A. Yedjour and B. v. Tiggelen, EPJD 59, 249 (2010) M. Piraud, L. Pezzé and L. Sanchez-Palencia, NJP 15, 075007 (2013) Improvement: take into account the shift of the lower bound of the energy spectrum (real part of self-energy) via selfconsistent Born approximation Correctly predict that Ec is negative for blue speckles but… 1) the value of Ec is not very accurate; contributions from all order in V 0 are important! 2) They predict same value of Ec for blue and red speckles, because the approximate self-energy is the same!

Outline Anderson localization with cold atoms in laser speckles Numerical computation of the mobility edge Self-consistent theory of localization On site-distribution and blue-red asymmetry Role of the spatial correlation function Comparison with experiments

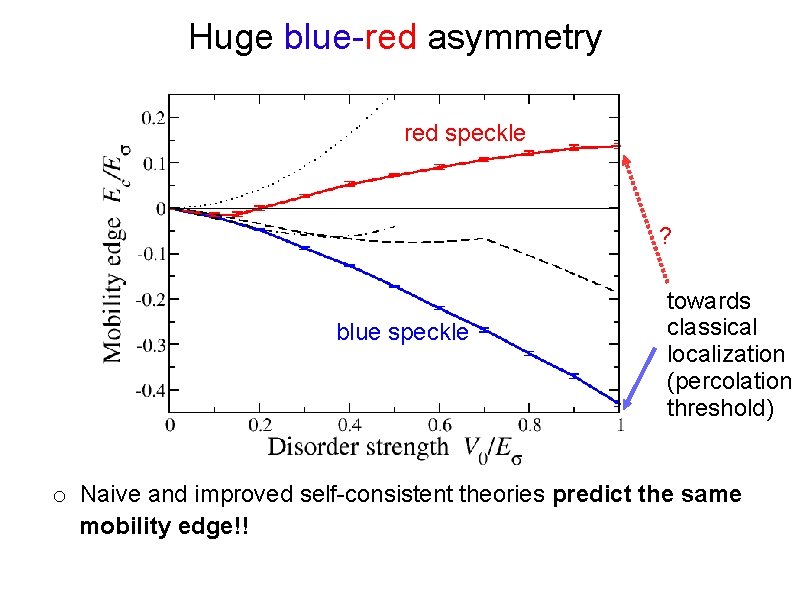
Huge blue-red asymmetry red speckle ? blue speckle towards classical localization (percolation threshold) o Naive and improved self-consistent theories predict the same mobility edge!!

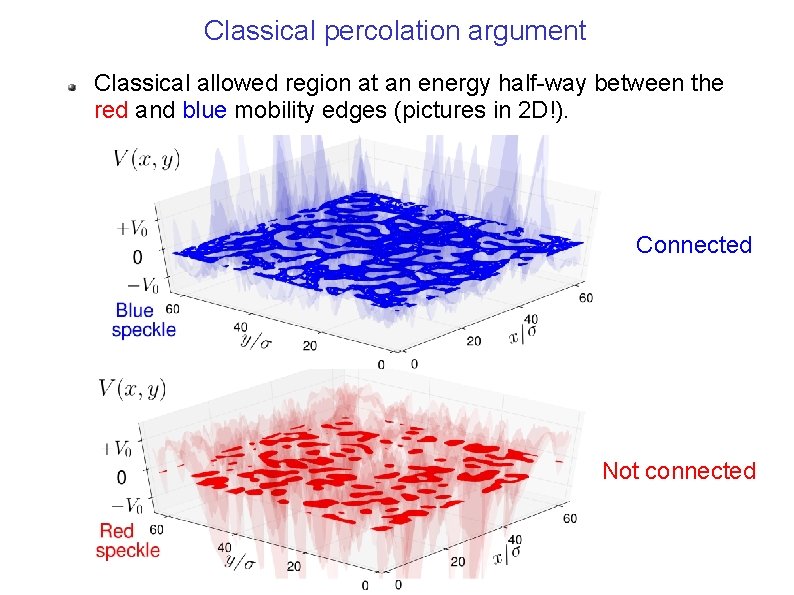
Classical percolation argument Classical allowed region at an energy half-way between the red and blue mobility edges (pictures in 2 D!). Connected Not connected

Outline Anderson localization with cold atoms in laser speckles Numerical computation of the mobility edge Self-consistent theory of localization On site-distribution and blue-red asymmetry Role of the spatial correlation function Comparison with experiments

How important are details of spatial correlation function for speckle? We compute Ec for different correlation functions having the same “width″ σ Almost no effect! At the mobility edge, disorder is so strong that details of the spatial correlation function are completely smoothed out => only the correlation length s matters

Outline Anderson localization with cold atoms in laser speckles Numerical computation of the mobility edge Self-consistent theory of localization On site-distribution and blue-red asymmetry Role of the spatial correlation function Comparison with experiments

Comparison with experimental results Three experimental measurements of the mobility edge. Mobility edge higher than our numerical predictions. B. De Marco (Urbana Champaign). Much too high mobility edge, strange properties of the atomic momentum/energy distributions. V. Josse (Palaiseau). Anisotropic disordered potential, relatively low fraction of atoms below the mobility edge. Measured mobility edge below zero, but still too high. G. Modugno (Florence). Anisotropic disordered potential. Large localized fraction. Qualitative behavior of the mobility edge with V 0 in fair agreement. Mobility edge seems a bit too high. Anderson transition is second order transition => atoms with energy close to the mobility edge diffuse very slowly. Maybe responsible for overestimation of the mobility edge? Numerical calculation with anisotropic disorder are needed, but difficult. Work in progress.

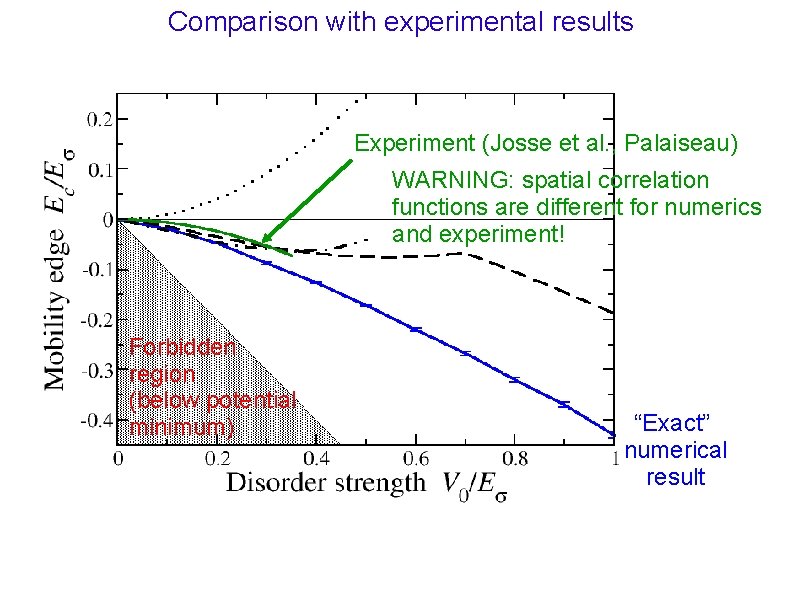
Comparison with experimental results Experiment (Josse et al. , Palaiseau) WARNING: spatial correlation functions are different for numerics and experiment! Forbidden region (below potential minimum) “Exact” numerical result

Summary It is possible to compute numerically the mobility edge for non-interacting cold atoms in a 3 D spatially correlated potential. Can be computed for any type of on-site potential distribution and any not-too-anisotropic spatial correlation function. Work in progress for anisotropic potentials. Large blue-red asymmetry. Partial failure of the self-consistent theory of localization, mainly because some quantities are computed at the Born approximation. Main features can be understood from P(V) distribution