Workshop for CSAP Teachers Sorting and Big O

Workshop for CS-AP Teachers Sorting and Big O Barb Ericson July 2006

Learning Objectives • Understand at the conceptual level – The need to group objects – Limitations of Arrays – Collections – Lists and Linked Lists – Sets and Maps – Stacks and Queues – Trees

Grouping Objects • We often group objects – A list of items to buy at a grocery store – Your friends names and phone numbers – Your homework for each class – A record of all of your ancestors – A sorted list of people in a class

Array Limitations • You can use arrays to store multiple objects – You need to know many items there will be • You specify the size when you create an array Item[] shopping. List = new Item[10]; – What happens if the array runs out of space? • If you try to add an element passed the last valid index you get – java. lang. Array. Index. Out. Of. Bounds. Exception • You could create a bigger array • You would have to copy all the elements from the old array to the new array – What if you don’t need all the space in an array?

Collection Classes • Java has collection classes to handle grouping objects – The classes don’t require you to know how many objects you will need to store • The collections will grow and shrink as needed • There are different types of collections depending on what you need – Keep the order of the objects - List – Make sure there are no duplicates – Set – Associate one object with another - Map

Collection Exercise • Look up the Collection Interface – How do you add objects to a collection? – Is there a way to add two collections together? – Is there a way to get an intersection of two collections? – Is there a way to remove an object from a collection? – How do you empty a collection? – Can you get an array from a collection?

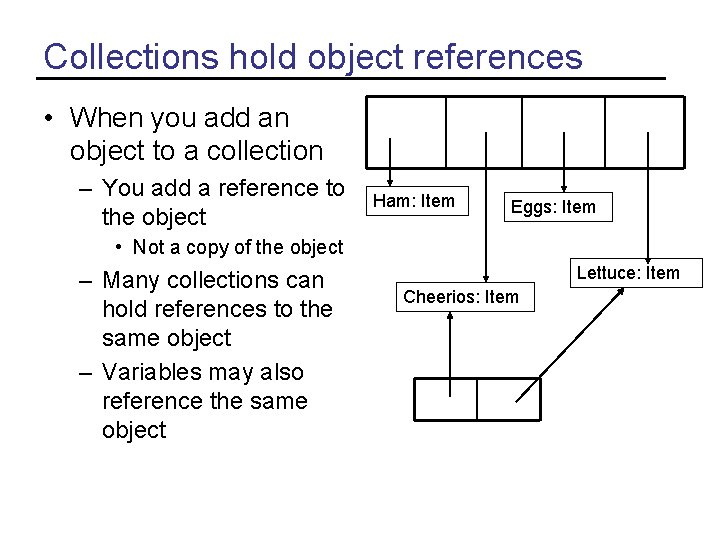
Collections hold object references • When you add an object to a collection – You add a reference to the object Ham: Item Eggs: Item • Not a copy of the object – Many collections can hold references to the same object – Variables may also reference the same object Lettuce: Item Cheerios: Item

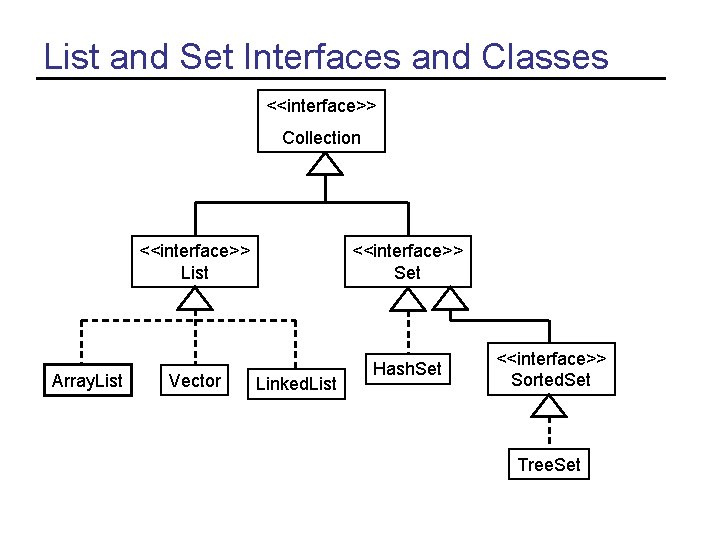
List and Set Interfaces and Classes <<interface>> Collection <<interface>> List Array. List Vector <<interface>> Set Linked. List Hash. Set <<interface>> Sorted. Set Tree. Set

List • We often keep ordered lists of things – “To do” list – People in a line – Parts • A list has an order – First thing, second thing, third thing, etc. • Lists may have duplicate items • You can get, add, or remove an item anywhere in a list

Java Lists • The first index is 0 – The last valid index is list. size() – 1 • Array. List is a class that implements the List interface – Using an array and allows null values in the list • Vector is an older class that also uses an array – It is like Array. List but it is synchronized • Linked. List is a class that implements the List interface – Using a linked structure, not an array

Linked List - java. util. Linked. List • A linked list has nodes that contain data and a reference to the next node head Sue Mary Tasha null • A doubly linked list has references to previous nodes as well null head Sue Mary Tasha null tail

Ideas for Teaching Linked Lists • Give random students a paper that tells them who the next and previous student is – Give one student the name of the first person in the list • Walk through – adding a new student to the front of the list – getting the 5 th person in the list – removing the 3 rd person in the list – removing the 1 st person in the list

Arrays versus Linked List • A book is like an array – The pages are ordered sequentially – It is easy to find a particular page • A magazine article is like a linked list – Has groups of pages and – a reference to the next group of pages • A treasure hunt is like a linked list – You start with one clue that takes you to the location of the next clue

Array. List versus Linked. List • If you need to access items randomly – Use an Array. List • Quick to access a random location • Can be slower to add to and remove from – If it needs to create a new array and copy old items • If you are doing lots of adding/removing from a list – Use a Linked. List • Quick to add to or remove from • Slow to do random access

Using Iterator • One way to access all elements of a List is to use a for loop and increment the index from 0 to < list. size() – Use the index to get items from the list item = item. List. get(index); • Another approach is to use an iterator Iterator<Item> iterator = item. List. iterator(); while (iterator. has. Next()) item = iterator. next();

Iterator Exercise • Is it better to use an iterator or an index to get all of the elements – of an Array. List? – of a Linked. List? • What about if you want to access every other element – of an Array. List? – of a Linked. List? • Which should you use if you don’t know the implementing class?

List. Iterator • Inherits from Iterator • Adds – The ability to traverse a list in either direction – The ability to modify the list during iteration • Add a new element before the current next element – public void add(Object obj); • Change the last accessed element – public void set(Object obj);

List. Node AP Class • Has value and next fields – Can get and set the fields • Has a constructor that take the value and next node • Uses the keyword null to indicate the end of the linked list List. Node Object value List. Node next public Object get. Value() public List. Node get. Next() public void set. Value(Object value) public void set. Next(List. Node node)

Loop through a linked list with List. Node • Start with a reference to the head of the list • Each time through the loop move the reference to the next node • Stop the loop when the reference is null – Continue while the reference is not null List. Node node = null; for (node = head; node != null; node = node. get. Next())

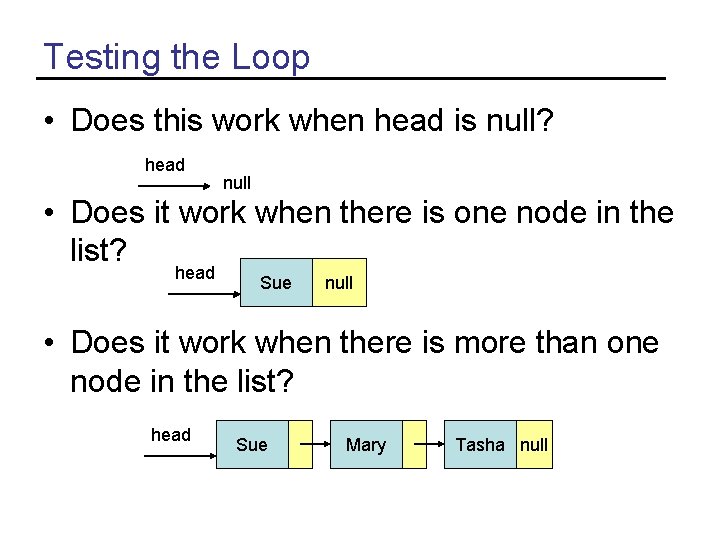
Testing the Loop • Does this work when head is null? head null • Does it work when there is one node in the list? head Sue null • Does it work when there is more than one node in the list? head Sue Mary Tasha null

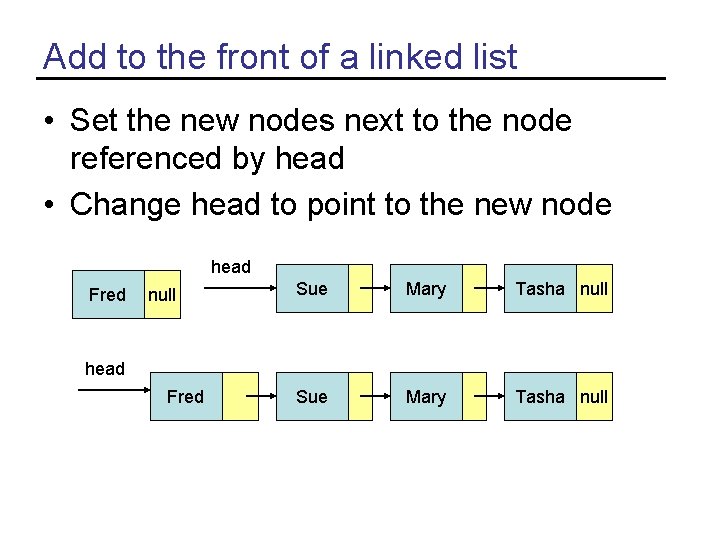
Add to the front of a linked list • Set the new nodes next to the node referenced by head • Change head to point to the new node head Fred null Sue Mary Tasha null head Fred

Stacks • A stack holds objects with the last object put in the stack being the first one returned – Last-in-first-out structure (LIFO) • Like a stack of cafeteria plates • Or a holder for bathroom cups • Or a Pez container • Stacks are used to hold the list of operations that you might want to undo – When you click “Undo” the last thing you did is undone

Teaching Stacks • Have each student put a book on a stack of books – Then ask a student to take off a book from the stack • Where did people put the new books? • Where did people take books from?

Stack Class • Java 5. 0 has a Stack Class – class java. util. Stack<E> – E push(E x) • Add x to the top of the stack – E pop() • Remove the top of the stack and return it – E peek() • Return the top item on the stack – boolean is. Empty() • Return true if the stack is empty

Queues • A queue holds objects with the first object put in the queue the first one returned – First-in-first-out structure (FIFO) • Like the ticket line at the movies • Or a car wash with cars moving through • Use queues to track events and objects – A queue of requests for printing • Handle the first one before the next one – A queue of people in line to buy tickets for a movie • People at the front of the queue buy tickets first

Teaching Queues • Have some students form a line as if in line to buy tickets for a movie – Who should be waited on first? Who would be waited on next? – When new people come where do they enter the line?

Queue Interface • java. util. Queue has a Queue Interface • Implemented by two Classes – java. util. Linked. List – Java. util. Priority. Queue • New methods – boolean add(E x) • Add to the end (tail) of the queue – E remove() • Remove front of queue and return it – E peek() • Return the front of the queue – boolean is. Empty() • Return true if the queue is empty

Set • A set does not preserve order – The order things are retrieved from a set is not necessarily the same order they were placed in a set • Sets do not allow duplicate elements – element. A. equals(element. B) – If you try to add an element that is equal to another element of the set it won’t add it • And will return false

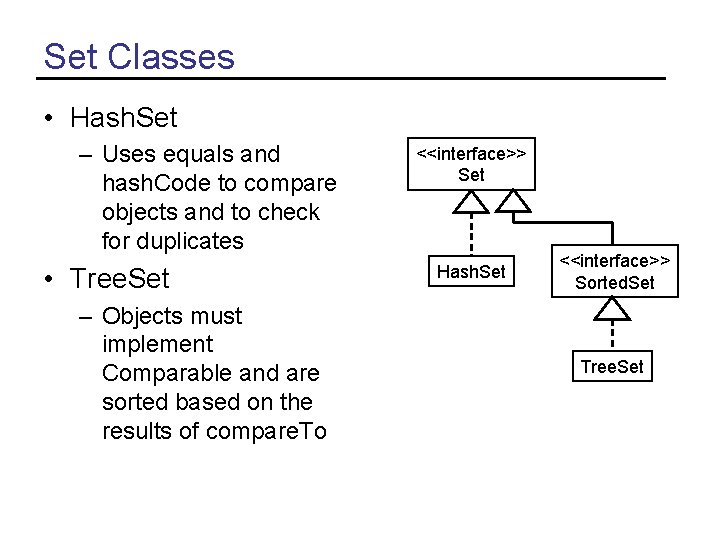
Set Classes • Hash. Set – Uses equals and hash. Code to compare objects and to check for duplicates • Tree. Set – Objects must implement Comparable and are sorted based on the results of compare. To <<interface>> Set Hash. Set <<interface>> Sorted. Set Tree. Set

Maps • Maps hold key and value pairs – Use a key to put a value into the map – Use a key to get a value from a map – There can’t be duplicate keys – There can be duplicate values • A value can be associated with different keys • Used to look up associated data – Like look up a customer record from a phone number – Or like safety deposit boxes

Map Interface • Get the number of keys in the map public int size(); • Put a value in the map for the given key – Returns the old object stored for this key public Object put(Object key, Object value); • Get a value from the map for the given key public Object get(Object key); • Check if the key is used in the map public boolean contains. Key(Object key); • Get a set of the keys used in the map public Set key. Set();

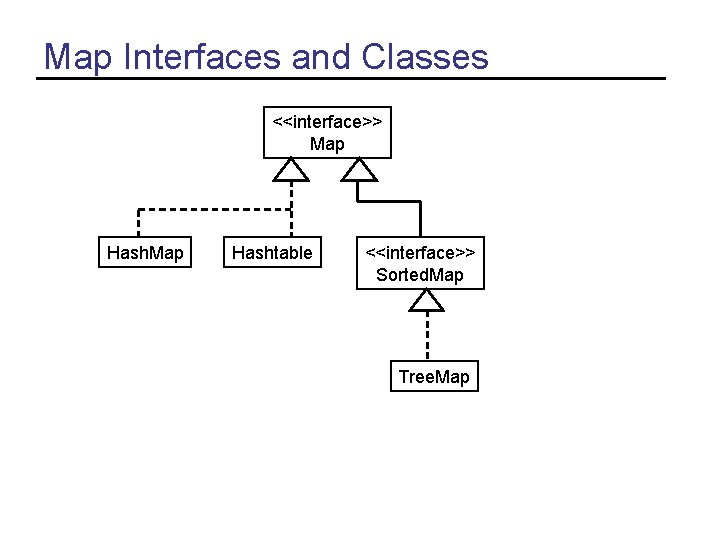
Map Interfaces and Classes <<interface>> Map Hashtable <<interface>> Sorted. Map Tree. Map

Map Classes • Hash. Map – Stores keys and values without regards to order entered – Allows null values and a null key • Hashtable – Older class like Hash. Map – Synchronized • Tree. Map – Holds keys in sorted order

Hashing • Hash. Map and Hashtable use hashing on the key to find the location where the value is stored – Using the hash. Code() method inherited from Object – This method is overridden for String – You should override this method in your classes • Maps the key to an index in an array

Hashing Procedure • When you put a value in a Hash. Map for a key – First the hash. Code method is called on the key object – This returns an int value which is mapped from 0 to the array length – 1 • Often by using remainder (%) – There may be a value at that index from a different key • This is called a collision

Handling Collisions • The array is often an array of lists – A bucket that holds more than one hash node – A good hash. Code() method should result in few collisions and small lists • When more than one key has the same index – The hash node is added to the list • When you look for a value based on a key – If it maps to an index with a list • It looks for the key using equals

hash. Code() Method • The goal is to get a good spread of int results • Use some combination of fields – Like the hash. Code for some String fields added to some prime number times some other field • Different keys can result in the same hash. Code() result • The same key object must give the same hash. Code() result

Trees • Linked lists have nodes that hold a value and a reference to the “next” node • What if you need to track more than one “next” node? – Like you want to record your ancestors • You can use a tree – Each tree node has a value (a person) – And a reference to the person’s mother – And a reference to the person’s father

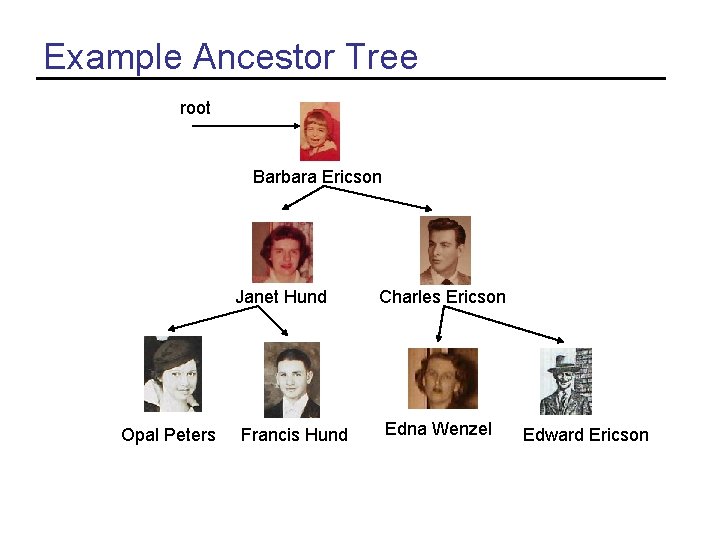
Example Ancestor Tree root Barbara Ericson Janet Hund Opal Peters Francis Hund Charles Ericson Edna Wenzel Edward Ericson

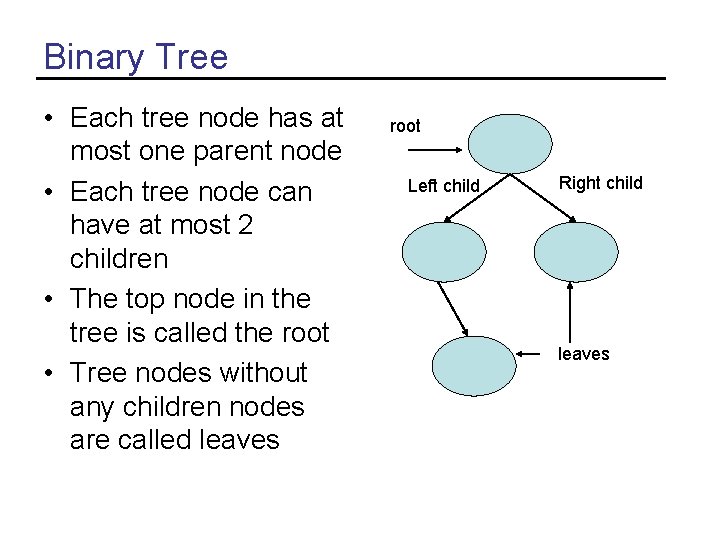
Binary Tree • Each tree node has at most one parent node • Each tree node can have at most 2 children • The top node in the tree is called the root • Tree nodes without any children nodes are called leaves root Left child Right child leaves

Tree Node AP Class • Has fields: value, left, and right • Can get and set all fields • Has a constructor that takes a value, left tree node and right tree node Tree. Node private Object value private Tree. Node left private Tree. Node right public Object get. Value() public Tree. Node get. Left() public Tree. Node get. Right() public void set. Value(Object o) public void set. Left(Tree. Node n) public void set. Right(Tree. Node n)

Trees are Recursive • Each tree node is the root of a sub-tree of the original tree • This allows the use of recursion – A method invokes itself • On a subset of the original problem • Like a subtree – There has to be an end condition • That stops the recursion • No more subtrees

Get the Number of Nodes in a Tree • If the root is null – The number of nodes is 0 • If the root isn’t null – Add one to the count – Add to the count the number of nodes in the left subtree – Add to the count the number of nodes in the right subtree

Get the Number of Nodes Method • Some books use a class (static) method to count the number of nodes – And pass in the current node public static int get. Num. Nodes(Tree. Node node) { if (node == null) return 0; else return 1 + get. Num. Nodes(node. get. Left()) + get. Num. Nodes(node. get. Right()); }

What is wrong with this? • Static methods are used when there is no current object – Or for general methods • In this case there is a current tree node – And the method does operate on it – It is explicitly passed to the method • So this should be an object method – And the current object should be implicitly passed

Modified Get Number of Nodes public int get. Num. Nodes() { int count = 0; // increment count = count + 1; // add to the count the number of nodes in the left subtree if (left != null) count = count + left. get. Num. Nodes(); // add the to count the number of nodes in the right subtree if (right != null) count = count + right. get. Num. Nodes(); return count; }

Tree class get. Num. Nodes() public int get. Num. Nodes() { int count = 0; // the default is no nodes // if the root isn't null get the number of nodes if (root != null) count = root. get. Num. Nodes(); return count; }

Tree Traversals • In-order traversal (left-data-right) – Do the recursive call on the left subtree – Do something with the value at the node – Do the recursive call on the right subtree • Pre-order traversal (data-left-right) – Do something with the value at the node – Do the recursive call on the left subtree – Do the recursive call on the right subtree • Post-order traversal (left-right-data) – Do the recursive call on the left subtree – Do the recursive call on the right subtree – Do something with the value at the node

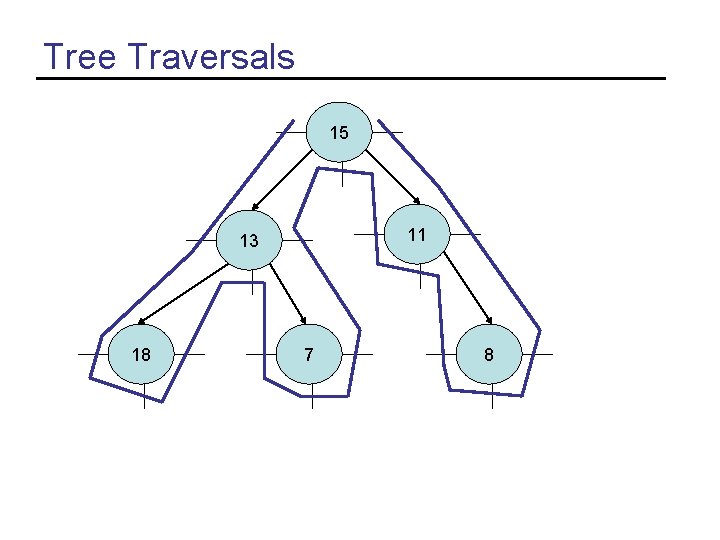
Tree Traversals 15 11 13 18 7 8

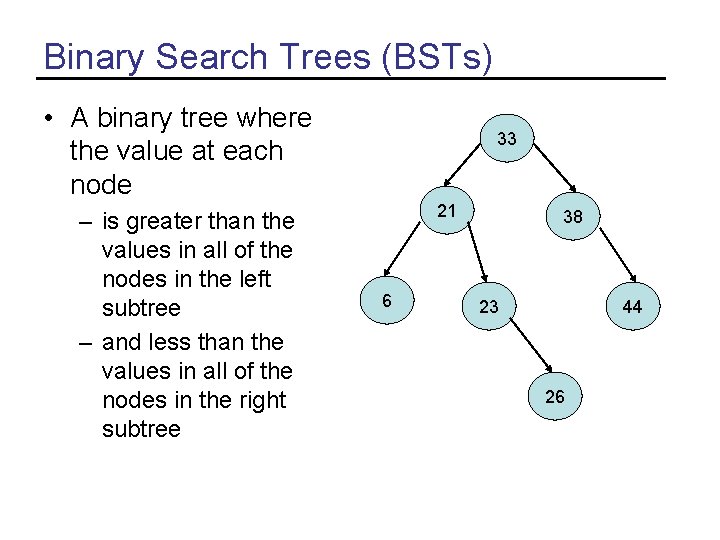
Binary Search Trees (BSTs) • A binary tree where the value at each node – is greater than the values in all of the nodes in the left subtree – and less than the values in all of the nodes in the right subtree 33 21 6 38 23 44 26

Binary Search Tree • Orders values – Usually using the Comparable Interface • Allows for quick search – For a “well filled” tree O(log n) – And quick insertion and deletion of nodes • An in-order traversal of a BST will give values in ascending order • Used by Tree. Set and Tree. Map

Priority Queue • Used to store items with various priorities – Like printer requests – Or airplanes waiting to land • Can hold several items with the same priority • Can item an object to the queue • Can get the item with the highest priority – Often considered to be the “minimum” item

Priority. Queue Class

Priority. Queue Class • class java. util. Priority. Queue<E> • boolean add(E x) – Add the passed item to the queue • E remove() – Remove top of the queue and return it • E peek() – Return the top item on the queue • boolean is. Empty() – Return true if the queue is empty

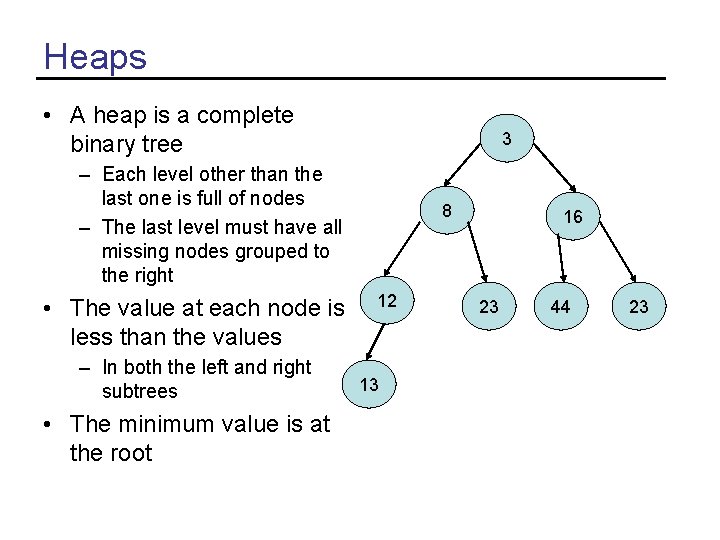
Heaps • A heap is a complete binary tree 3 – Each level other than the last one is full of nodes – The last level must have all missing nodes grouped to the right • The value at each node is less than the values – In both the left and right subtrees • The minimum value is at the root 8 12 13 16 23 44 23

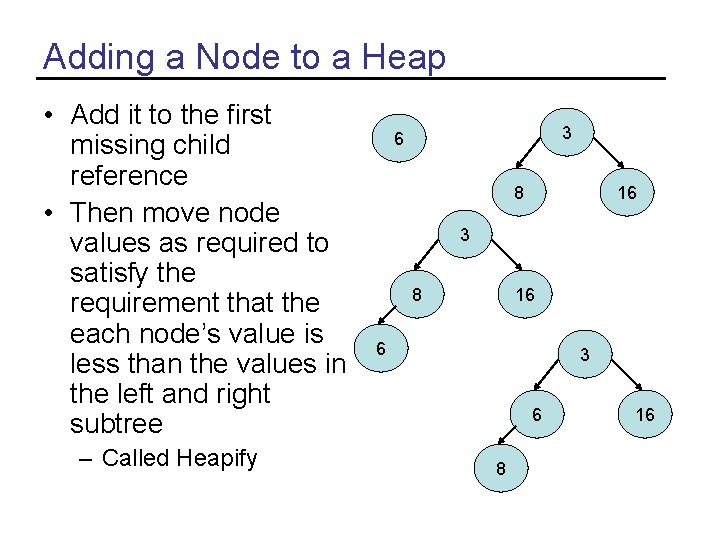
Adding a Node to a Heap • Add it to the first missing child reference • Then move node values as required to satisfy the requirement that the each node’s value is less than the values in the left and right subtree – Called Heapify 3 6 8 16 3 8 16 6 3 6 8 16

Data Structures Exercise • What data structure would you use to hold a known number of students in an order? • What data structure would you use to store your friends names and cell phone numbers? • What data structure would you use to store orders in a fast-food restaurant? • What data structure would you use to store recent commands to allow undo? • What data structure would you use to store a sorted list of teachers?

Summary • Collection classes hold groups of objects – Collections can grow and shrink • Lists hold objects in order and allow duplicate objects – Linked lists have nodes that hold a value and a reference to the next node • Doubly linked list nodes also hold a reference to the previous node • Sets hold objects without preserving order and do not allow duplicate objects in the set • Maps associate a key object with a value object • Trees have nodes that hold values and references to children nodes