WORKSHEET KEY 1 2 3 4 5 Yes
- Slides: 29
WORKSHEET KEY 1) 2) 3) 4) 5) Yes No No (6, 6), (– 3, – 3), (0, 3) A’ (– 8, 8), B’ (4, 8), C’ (– 4, – 4) 3/6/2021 3: 10 AM 8) 7/13 9) 4 10) 1/3 11) C 12– 7: Tessellations 1
3/6/2021 3: 10 AM 12– 7: Tessellations 2
MONDAY FUN DAY 3/6/2021 3: 10 AM 12– 7: Tessellations 3
TESSELLATIONS Section 12– 7 Geometry Pre. AP, Revised © 2014 viet. dang@humble. k 12. tx. us 3/6/2021 3: 10 AM 12– 7: Tessellations 4
REVIEW A. Find the sum of the interior angle measures of each polygon. 1. Quadrilateral 2. Octagon 360° 1080° B. Find the interior angle measure of each regular polygon. 1. Square 90° 2. Pentagon 108° 3. Hexagon 120° 4. Octagon 135° 3/6/2021 3: 10 AM 12– 7: Tessellations 5
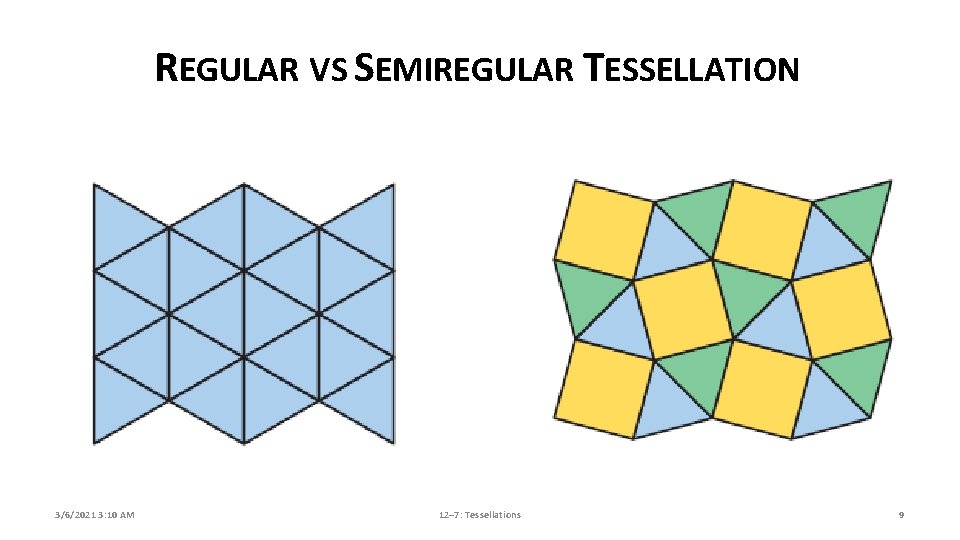
TESSELLATIONS A. A tessellation, or tiling, A Tessellation is a collection of shapes that fit together to cover a surface without overlapping or leaving gaps. B. Greek word, Tessella which means “four” C. Three regular shapes (all sides and angles) can be made to tessellations 1. Equilateral Triangles: 60° 2. Squares: 90° 3. Hexagons: 120° D. A semiregular tessellation is formed by two or more different regular polygons 3/6/2021 3: 10 AM 12– 7: Tessellations 6
VIDEO http: //www. youtube. com/watch? v=t. JYt. BF 6 gt 4 c 3/6/2021 3: 10 AM 12– 7: Tessellations 7
REAL WORLD EXAMPLES 3/6/2021 3: 10 AM Brick Walls Floor Tiles Checkerboard s Honeycombs Textile Patterns Art 12– 7: Tessellations 8
REGULAR VS SEMIREGULAR TESSELLATION 3/6/2021 3: 10 AM 12– 7: Tessellations 9
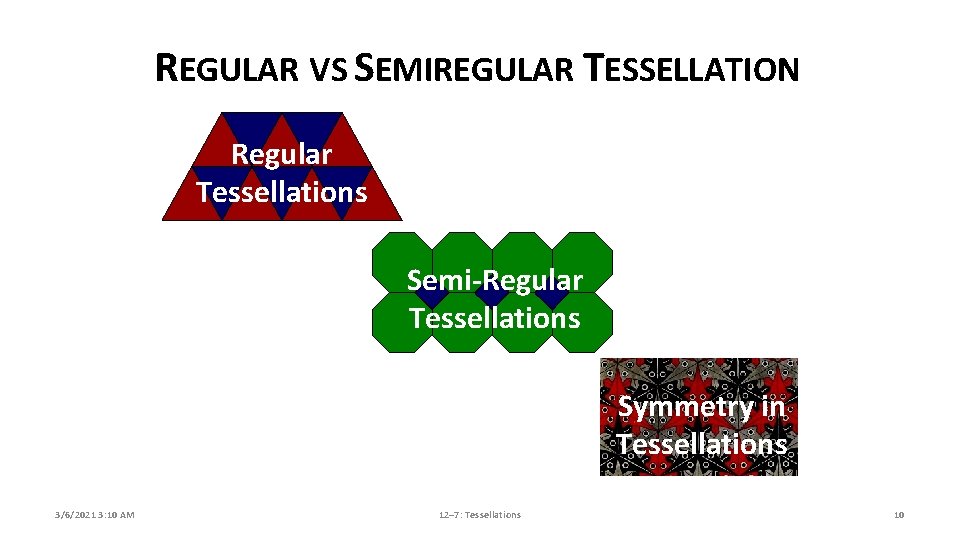
REGULAR VS SEMIREGULAR TESSELLATION Regular Tessellations Semi-Regular Tessellations Symmetry in Tessellations 3/6/2021 3: 10 AM 12– 7: Tessellations 10
STEPS A. Rotate the quadrilateral 180° about the midpoint of one side. B. Translate the resulting pair of triangles to make a row C. Translate the row of quadrilaterals to make a tessellation. 3/6/2021 3: 10 AM 12– 7: Tessellations 11
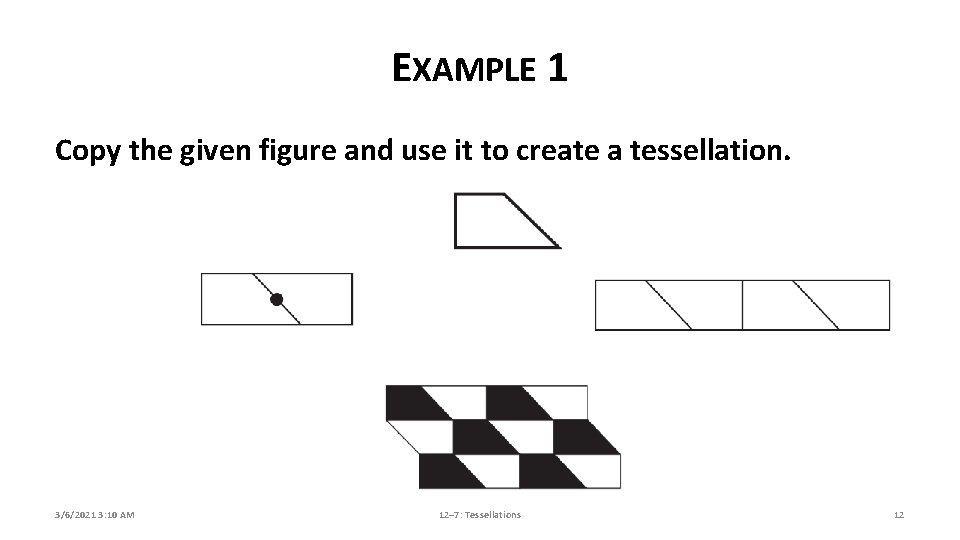
EXAMPLE 1 Copy the given figure and use it to create a tessellation. 3/6/2021 3: 10 AM 12– 7: Tessellations 12
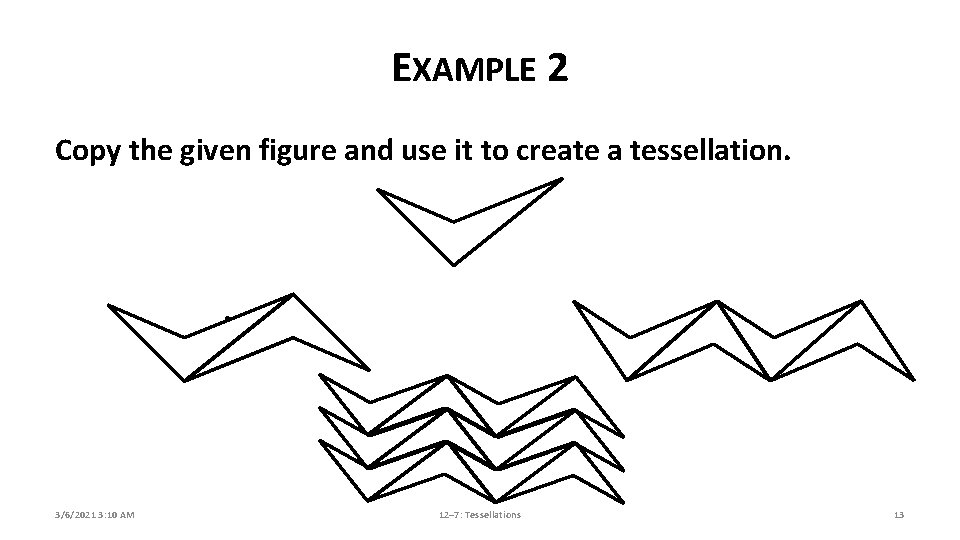
EXAMPLE 2 Copy the given figure and use it to create a tessellation. 3/6/2021 3: 10 AM 12– 7: Tessellations 13
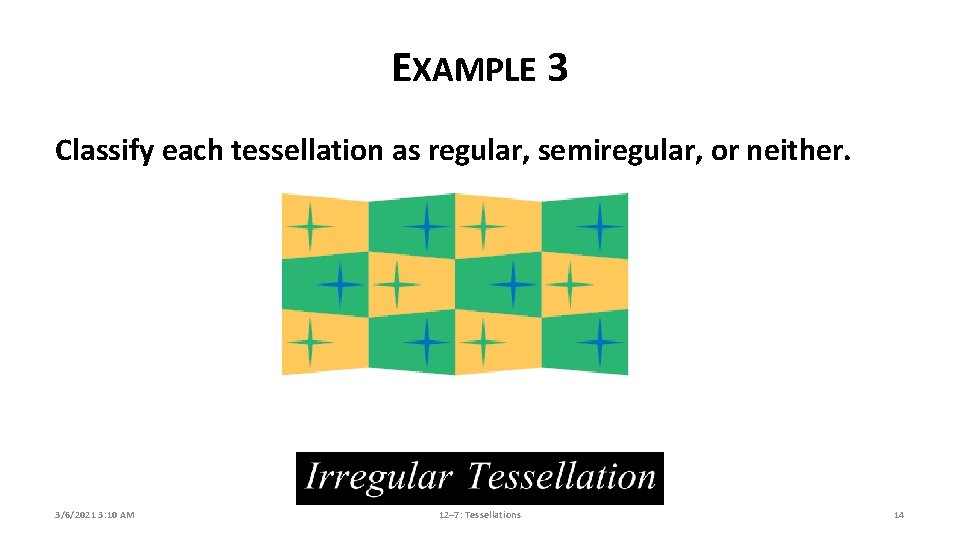
EXAMPLE 3 Classify each tessellation as regular, semiregular, or neither. 3/6/2021 3: 10 AM 12– 7: Tessellations 14
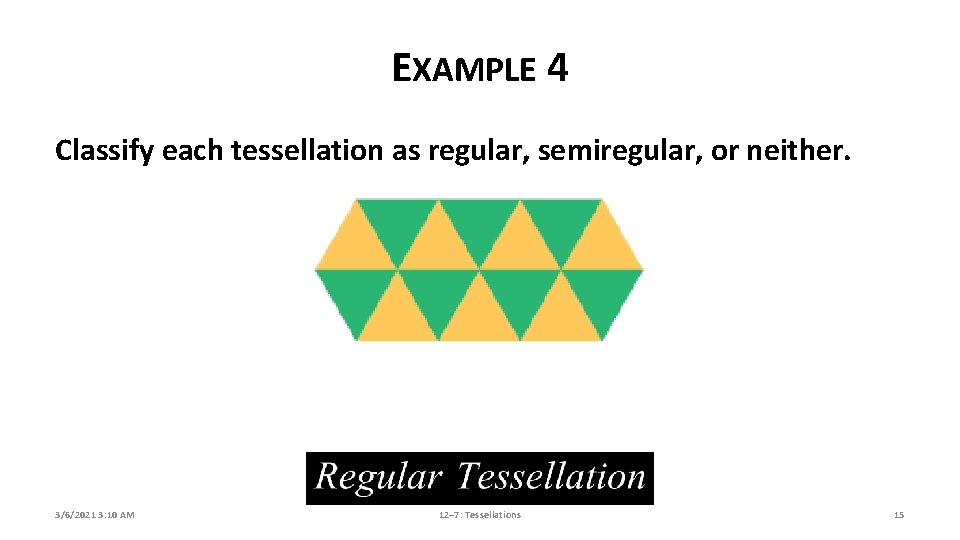
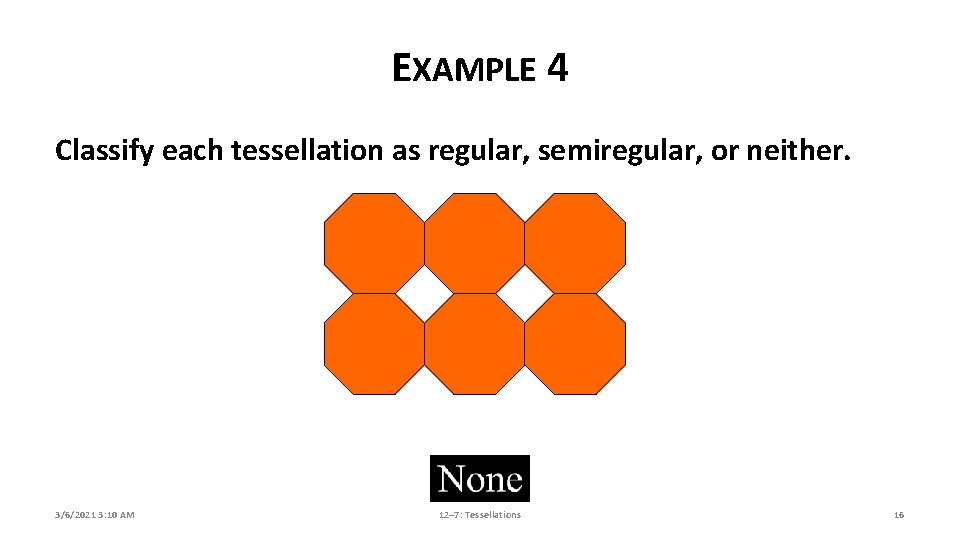
EXAMPLE 4 Classify each tessellation as regular, semiregular, or neither. 3/6/2021 3: 10 AM 12– 7: Tessellations 15
EXAMPLE 4 Classify each tessellation as regular, semiregular, or neither. 3/6/2021 3: 10 AM 12– 7: Tessellations 16
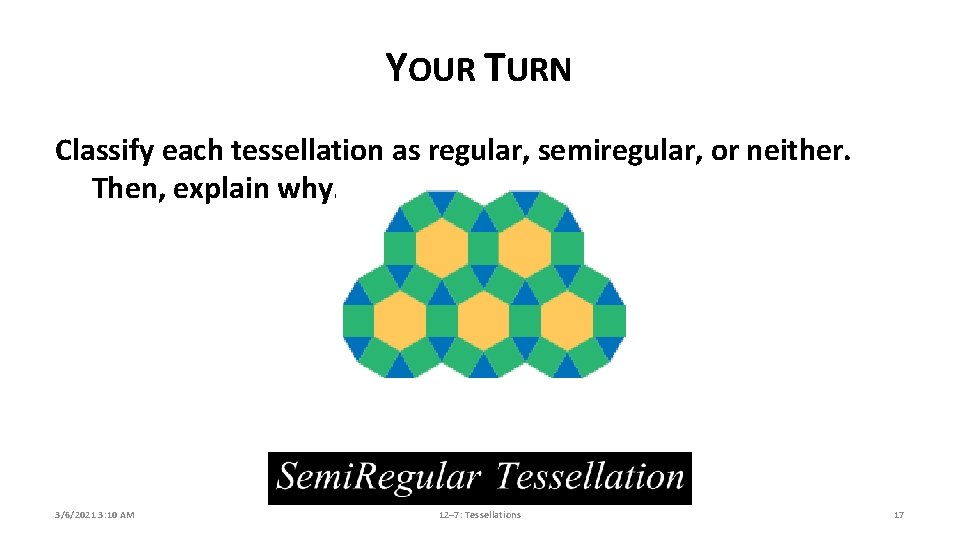
YOUR TURN Classify each tessellation as regular, semiregular, or neither. Then, explain why. 3/6/2021 3: 10 AM 12– 7: Tessellations 17
TYPES OF TESSELLATIONS A. B. C. D. Rotations Translations Reflection Glide Translation 3/6/2021 3: 10 AM 12– 7: Tessellations 18
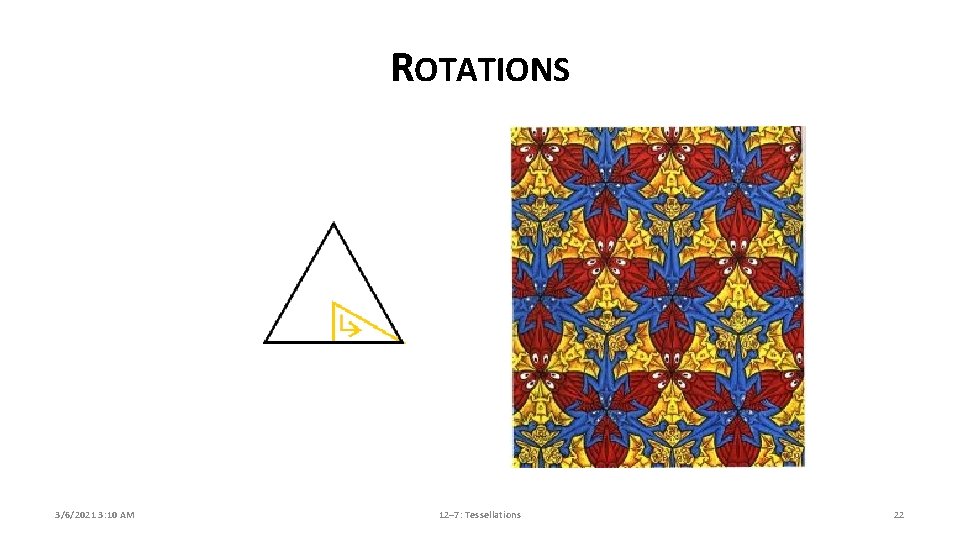
ROTATIONS A. To rotate an object means to turn it around. Every rotation has a center and an angle. A tessellation possesses rotational symmetry if it can be rotated through some angle and remain unchanged. B. Examples of objects with rotational symmetry include automobile wheels, flowers, and kaleidoscope patterns. 3/6/2021 3: 10 AM 12– 7: Tessellations 19
ROTATIONS 3/6/2021 3: 10 AM 12– 7: Tessellations 20
ROTATIONS 3/6/2021 3: 10 AM 12– 7: Tessellations 21
ROTATIONS 3/6/2021 3: 10 AM 12– 7: Tessellations 22
TRANSLATIONS A. To translate an object means to move it without rotating or reflecting it. Every translation has a direction and a distance. A tessellation possesses translational symmetry if it can be translated (moved) by some distance and remain unchanged. B. A tessellation or pattern with translational symmetry is repeating, like a wallpaper or fabric pattern. 3/6/2021 3: 10 AM 12– 7: Tessellations 23
TRANSLATIONS 3/6/2021 3: 10 AM 12– 7: Tessellations 24
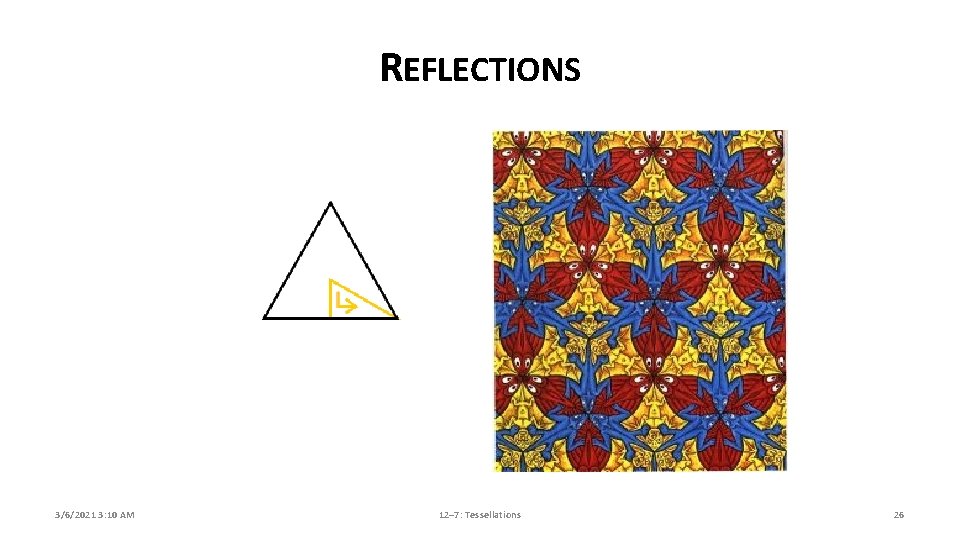
REFLECTIONS TRANSLATIONS A. To reflect an object means to produce its mirror image. Every reflection has a mirror line. A tessellation possesses reflection symmetry if it can be mirrored about a line and remain unchanged. A reflection of an “R” is a backwards “R”. 3/6/2021 3: 10 AM 12– 7: Tessellations 25
REFLECTIONS 3/6/2021 3: 10 AM 12– 7: Tessellations 26
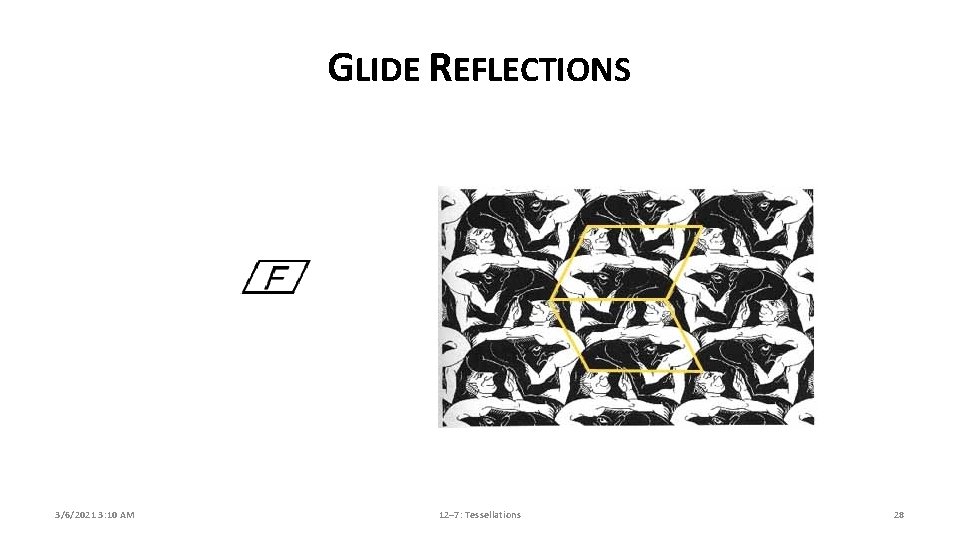
GLIDE REFLECTIONS A. A glide reflection combines a reflection with a translation along the direction of the mirror line. Glide reflections are the only type of symmetry that involve more than one step. A tessellation possesses glide reflection symmetry if it can be translated by some distance and mirrored about a line and remain unchanged. B. A real world example is footsteps! 3/6/2021 3: 10 AM 12– 7: Tessellations 27
GLIDE REFLECTIONS 3/6/2021 3: 10 AM 12– 7: Tessellations 28
ASSIGNMENT Worksheet 3/6/2021 3: 10 AM 12– 7: Tessellations 29
Yes i said yes i will yes analisi
Im trading
Cloudcap piccolo
Trading
Worksheet constitution worksheet answer key
Which key resources are we acquiring from partners
Key partners
Yes you may gif
Yes ma'am writing
Unhappy darling?
Which angle
Would you like bananas
Do you like bananas yes i do
Yes, there is.
Say yes tobias wolff summary
Present simple question
Does copper have uniform composition
Questions and short answers
R3 yes list
Do you speak english yes i do
Are viruses alive yes or no
Yes waiver
Do you like bananas
Past progressive yes no questions
1.look read and number
We are one nation yes we are one land lyrics
Yes bank hierarchy structure
Yes and no in asl
I am you are he is she is it is we are you are they are
Situation-producing questions example
