Worklist algorithm Initialize all di to the empty

Worklist algorithm let m: map from edge to computed value at edge let worklist:

Termination • Why is termination important? • Can we stop the algorithm in the

Termination • Assuming we’re doing reaching defs, let’s try to guarantee that the worklist

Structure of the domain • We’re using the structure of the domain outside of

Relations • A relation over a set S is a set R µ S

Partial orders • An equivalence class is a relation that is: • A partial

Partial orders • An equivalence class is a relation that is: – reflexive, transitive,

Lub and glb • Given a poset (S, ·), and two elements a 2

Lattices • A lattice is a tuple (S, v, ? , >, t, u)

Examples of lattices • Booleans expressions

Back to our example let m: map from edge to computed value at edge

Back to our example • We formalize our domain with a powerset lattice •

Direction of lattice • Unfortunately: – dataflow analysis community has picked one direction –

Direction of lattice • Always safe to go up in the lattice • Can

Worklist algorithm using lattices let m: map from edge to computed value at edge

Termination of this algorithm? • For reaching definitions, it terminates. . . • Why?

Termination • Still, it’s annoying to have to perform a join in the worklist

Even more formal • To reason more formally about termination and precision, we re-express

Fixed points • Recall, we are computing m, a map from edges to dataflow

Fixed points • We want to find a fixed point of F, that is

Fixed points • Formally: • We would like the sequence Fi(? ) for i

Back to termination • So if F is monotonic, we have what we want:

Another benefit of monotonicity • Suppose Marsians came to earth, and miraculously give you

Another benefit of monotonicity • We are computing the least fixed point. . .

Recap • Let’s do a recap of what we’ve seen so far • Started

Worklist algorithm for reaching defns let m: map from edge to computed value at

Generalized algorithm using lattices let m: map from edge to computed value at edge

Next step: removed outer join • Wanted to remove the outer join, while still

Guarantees • If F is monotonic, don’t need outer join • If F is

What about if we start at top? • What if we start with >:

Another example: constant prop • Set D = in x : = N Fx

Another example: constant prop • Set D = 2 { x ! N |

Another example: constant prop in x : = *y Fx : = *y(in) =

Another example: constant prop in x : = *y out in *x : =

Another example: constant prop in *x : = *y + *z F*x : =

Another example: constant prop in s: if (. . . ) out[0] out[1] in[0]

Slides: 59

Download presentation

Worklist algorithm • Initialize all di to the empty set • Store all nodes onto a worklist • while worklist is not empty: – remove node n from worklist – apply flow function for node n – update the appropriate di, and add nodes whose inputs have changed back onto worklist

Worklist algorithm let m: map from edge to computed value at edge let worklist: work list of nodes for each edge e in CFG do m(e) : = ; for each node n do worklist. add(n) while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length-1 do if (m(n. outgoing_edges[i]) info_out[i]) m(n. outgoing_edges[i]) : = info_out[i]; worklist. add(n. outgoing_edges[i]. dst);

Termination • Why is termination important? • Can we stop the algorithm in the middle and just say we’re done. . . • No: we need to run it to completion, otherwise the results are not safe. . .

Termination • Assuming we’re doing reaching defs, let’s try to guarantee that the worklist loop terminates, regardless of what the flow function F does while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length-1 do if (m(n. outgoing_edges[i]) info_out[i]) m(n. outgoing_edges[i]) : = info_out[i]; worklist. add(n. outgoing_edges[i]. dst);

Termination • Assuming we’re doing reaching defs, let’s try to guarantee that the worklist loop terminates, regardless of what the flow function F does while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length-1 do let new_info : = m(n. outgoing_edges[i]) [ info_out[i]; if (m(n. outgoing_edges[i]) new_info]) m(n. outgoing_edges[i]) : = new_info; worklist. add(n. outgoing_edges[i]. dst);

Structure of the domain • We’re using the structure of the domain outside of the flow functions • In general, it’s useful to have a framework that formalizes this structure • We will use lattices

Background material

Relations • A relation over a set S is a set R µ S £ S – We write a R b for (a, b) 2 R • A relation R is: – reflexive iff 8 a 2 S. a. Ra – transitive iff 8 a 2 S, b 2 S, c 2 S. a R b Æ b R c ) a R c – symmetric iff 8 a, b 2 S. a R b ) b R a – anti-symmetric iff 8 a, b, 2 S. a R b ) : (b R a)

Partial orders • An equivalence class is a relation that is: • A partial order is a relation that is:

Partial orders • An equivalence class is a relation that is: – reflexive, transitive, symmetric • A partial order is a relation that is: – reflexive, transitive, anti-symmetric • A partially ordered set (a poset) is a pair (S, ·) of a set S and a partial order · over the set • Examples of posets: (2 S, µ), (Z, ·), (Z, divides)

Lub and glb • Given a poset (S, ·), and two elements a 2 S and b 2 S, then the: – least upper bound (lub) is an element c such that a · c, b · c, and 8 d 2 S. (a · d Æ b · d) ) c · d – greatest lower bound (glb) is an element c such that c · a, c · b, and 8 d 2 S. (d · a Æ d · b) ) d · c

Lattices • A lattice is a tuple (S, v, ? , >, t, u) such that: – – – (S, v) is a poset 8 a 2 S. ? va 8 a 2 S. av> Every two elements from S have a lub and a glb t is the least upper bound operator, called a join u is the greatest lower bound operator, called a meet

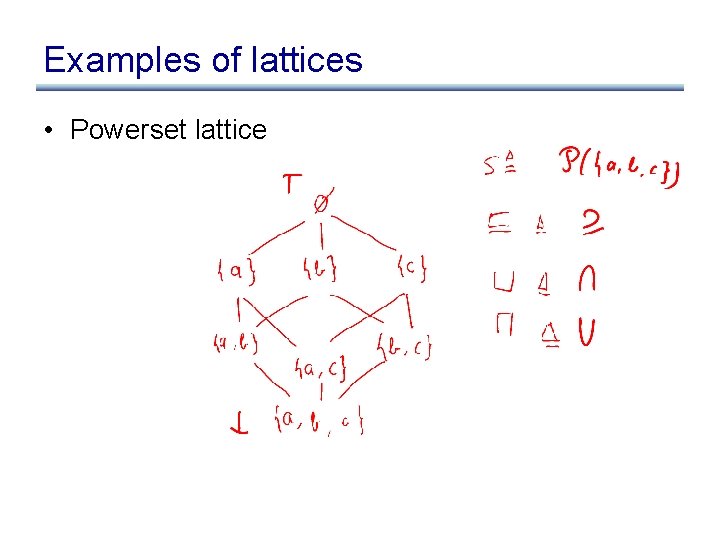
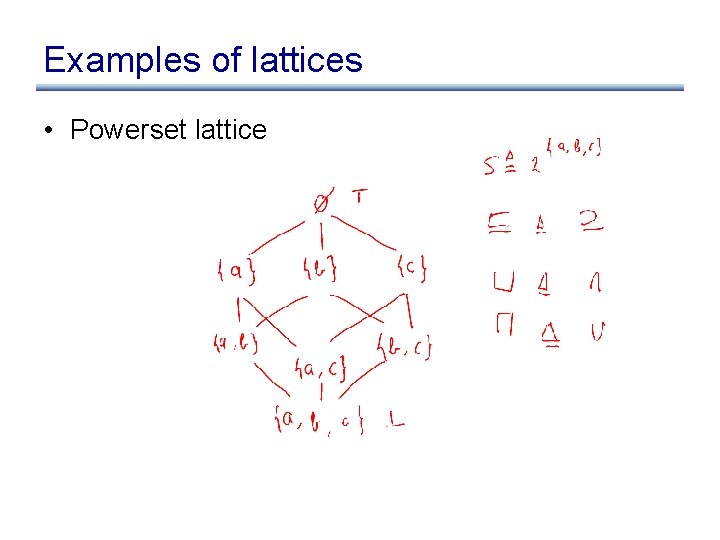
Examples of lattices • Powerset lattice

Examples of lattices • Booleans expressions

End of background material

Back to our example let m: map from edge to computed value at edge let worklist: work list of nodes for each edge e in CFG do m(e) : = ; for each node n do worklist. add(n) while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length do let new_info : = m(n. outgoing_edges[i]) [ info_out[i]; if (m(n. outgoing_edges[i]) new_info]) m(n. outgoing_edges[i]) : = new_info; worklist. add(n. outgoing_edges[i]. dst);

Back to our example • We formalize our domain with a powerset lattice • What should be top and what should be bottom?

Back to our example • We formalize our domain with a powerset lattice • What should be top and what should be bottom? • Does it matter? – It matters because, as we’ve seen, there is a notion of approximation, and this notion shows up in the lattice

Direction of lattice • Unfortunately: – dataflow analysis community has picked one direction – abstract interpretation community has picked the other • We will work with the abstract interpretation direction • Bottom is the most precise (optimistic) answer, Top the most imprecise (conservative)

Direction of lattice • Always safe to go up in the lattice • Can always set the result to > • Hard to go down in the lattice • So. . . Bottom will be the empty set in reaching defs

Worklist algorithm using lattices let m: map from edge to computed value at edge let worklist: work list of nodes for each edge e in CFG do m(e) : = ? for each node n do worklist. add(n) while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length do let new_info : = m(n. outgoing_edges[i]) t info_out[i]; if (m(n. outgoing_edges[i]) new_info]) m(n. outgoing_edges[i]) : = new_info; worklist. add(n. outgoing_edges[i]. dst);

Termination of this algorithm? • For reaching definitions, it terminates. . . • Why? – lattice is finite • Can we loosen this requirement? – Yes, we only require the lattice to have a finite height • Height of a lattice: length of the longest ascending or descending chain • Height of lattice (2 S, µ) =

Termination • Still, it’s annoying to have to perform a join in the worklist algorithm while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length do let new_info : = m(n. outgoing_edges[i]) t info_out[i]; if (m(n. outgoing_edges[i]) new_info]) m(n. outgoing_edges[i]) : = new_info; worklist. add(n. outgoing_edges[i]. dst); • It would be nice to get rid of it, if there is a property of the flow functions that would allow us to do so

Even more formal • To reason more formally about termination and precision, we re-express our worklist algorithm mathematically • We will use fixed points to formalize our algorithm

Fixed points • Recall, we are computing m, a map from edges to dataflow information • Define a global flow function F as follows: F takes a map m as a parameter and returns a new map m’, in which individual local flow functions have been applied

Fixed points • We want to find a fixed point of F, that is to say a map m such that m = F(m) • Approach to doing this? • Define ? , which is ? lifted to be a map: ? = e. ? • Compute F(? ), then F(F(? )), then F(F(F(? ))), . . . until the result doesn’t change anymore

Fixed points • Formally: • We would like the sequence Fi(? ) for i = 0, 1, 2. . . to be increasing, so we can get rid of the outer join • Require that F be monotonic: – 8 a, b. a v b ) F(a) v F(b)

Fixed points

Back to termination • So if F is monotonic, we have what we want: finite height ) termination, without the outer join • Also, if the local flow functions are monotonic, then global flow function F is monotonic

Another benefit of monotonicity • Suppose Marsians came to earth, and miraculously give you a fixed point of F, call it fp. • Then:

Another benefit of monotonicity • We are computing the least fixed point. . .

Recap • Let’s do a recap of what we’ve seen so far • Started with worklist algorithm for reaching definitions

Worklist algorithm for reaching defns let m: map from edge to computed value at edge let worklist: work list of nodes for each edge e in CFG do m(e) : = ; for each node n do worklist. add(n) while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length do let new_info : = m(n. outgoing_edges[i]) [ info_out[i]; if (m(n. outgoing_edges[i]) new_info]) m(n. outgoing_edges[i]) : = new_info; worklist. add(n. outgoing_edges[i]. dst);

Generalized algorithm using lattices let m: map from edge to computed value at edge let worklist: work list of nodes for each edge e in CFG do m(e) : = ? for each node n do worklist. add(n) while (worklist. empty. not) do let n : = worklist. remove_any; let info_in : = m(n. incoming_edges); let info_out : = F(n, info_in); for i : = 0. . info_out. length do let new_info : = m(n. outgoing_edges[i]) t info_out[i]; if (m(n. outgoing_edges[i]) new_info]) m(n. outgoing_edges[i]) : = new_info; worklist. add(n. outgoing_edges[i]. dst);

Next step: removed outer join • Wanted to remove the outer join, while still providing termination guarantee • To do this, we re-expressed our algorithm more formally • We first defined a “global” flow function F, and then expressed our algorithm as a fixed point computation

Guarantees • If F is monotonic, don’t need outer join • If F is monotonic and height of lattice is finite: iterative algorithm terminates • If F is monotonic, the fixed point we find is the least fixed point. • Any questions so far?

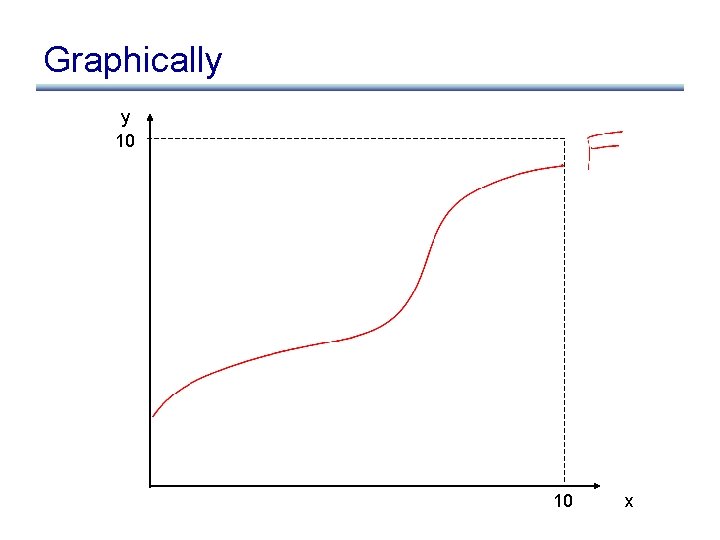
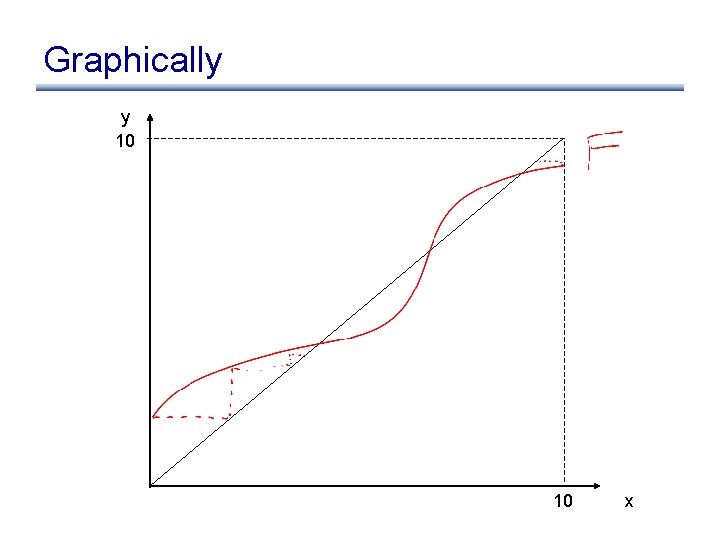
What about if we start at top? • What if we start with >: F(>), F(F(>)), F(F(F(>)))

What about if we start at top? • What if we start with >: F(>), F(F(>)), F(F(F(>))) • We get the greatest fixed point • Why do we prefer the least fixed point? – More precise

Graphically y 10 10 x

Graphically, another way

Another example: constant prop • Set D = in x : = N Fx : = N(in) = out in x : = y op z out Fx : = y op z(in) =

Another example: constant prop • Set D = 2 { x ! N | x 2 Vars Æ N 2 Z } in x : = N Fx : = N(in) = in – { x ! * } [ { x ! N } out in x : = y op z out Fx : = y op z(in) = in – { x ! * } [ { x ! N | ( y ! N 1 ) 2 in Æ ( z ! N 2 ) 2 in Æ N = N 1 op N 2 }

Another example: constant prop in x : = *y Fx : = *y(in) = out in *x : = y out F*x : = y(in) =

Another example: constant prop in x : = *y out in *x : = y out Fx : = *y(in) = in – { x ! * } [ { x ! N | 8 z 2 may-point-to(x). (z ! N) 2 in } F*x : = y(in) = in – { z ! * | z 2 may-point(x) } [ { z ! N | z 2 must-point-to(x) Æ y ! N 2 in } [ { z ! N | (y ! N) 2 in Æ (z ! N) 2 in }

Another example: constant prop in *x : = *y + *z F*x : = *y + *z(in) = out in x : = f(. . . ) out Fx : = f(. . . )(in) =

Another example: constant prop in *x : = *y + *z F*x : = *y + *z(in) = Fa : = *y; b : = *z; c : = a + b; *x : = c(in) out in x : = f(. . . ) out Fx : = f(. . . )(in) = ;

Another example: constant prop in s: if (. . . ) out[0] out[1] in[0] in[1] merge out