Working with bits Some observations on using x

Working with ‘bits’ Some observations on using x 86 bit-manipulations

Twos-complement extension • The following are legal statements in C: char short int c = -5; s = c; i = s; • They illustrate ‘type promotions’ of signed integers having different storage widths 11111011 ‘sign-extension’ 11111011 8 -bits 16 -bits The byte’s sign-bit is replicated throughout in the upper portion of the word

Sign-Extensions • The x 86 processor provides some special instructions for integer type-promotions: • • • CBW: CWDE: CDQE: CWD: CDQ: CQO: – movsx – movzx AX sign-extension of AL EAX sign-extension of AX RAX sign-extension of EAX DX: AX sign-extension of AX EDX: EAX sign-extension of EAX RDX: RAX sign-extension of RDX sign-extends source to destination zero-extends source to destination

Absolute value (naïve version) • Here is an amateur’s way of computing |x| in assembly language (test-and-branch): # # Replaces the signed integer in RAX with its absolute value # abs: cmp $0, %rax # is the value less than zero? jge isok # no, leave value unchanged neg %rax # otherwise negate the value isok: ret # return absolute value in RAX • But jumps flush the CPUs prefetch queue!

Absolute value (smart version) • Here is a professional’s way of computing |x| in assembly language (no branching): # # Replaces the signed integer in RAX with its absolute value # abs: cqo # sign-extend RAX to RDX: RAX xor %rdx, %rax # maybe flips all the bits in RAX sub %rdx, %rax # maybe subtracts -1 from RAX ret # return absolute value in RAX • No effect on positive integers, but ‘flips the bits and adds one’ for negative integers
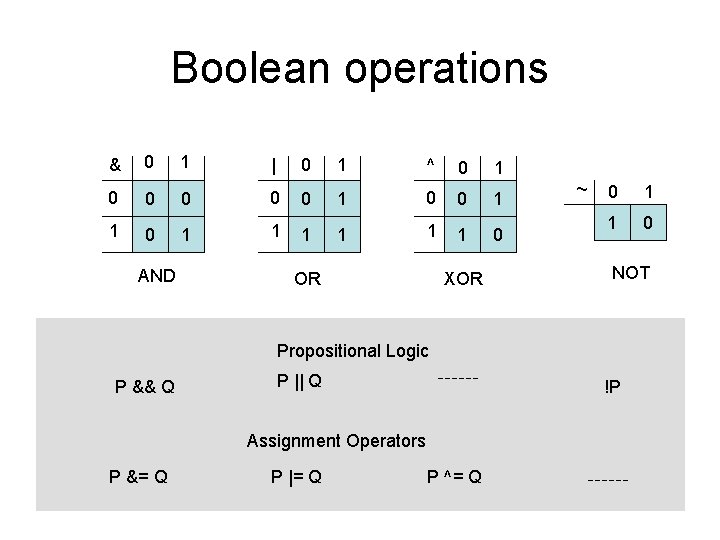
Boolean operations & 0 1 | 0 1 ^ 0 1 0 0 1 1 1 1 0 AND OR XOR ~ 0 1 1 0 NOT Propositional Logic P && Q P || Q !P Assignment Operators P &= Q P |= Q P ^= Q
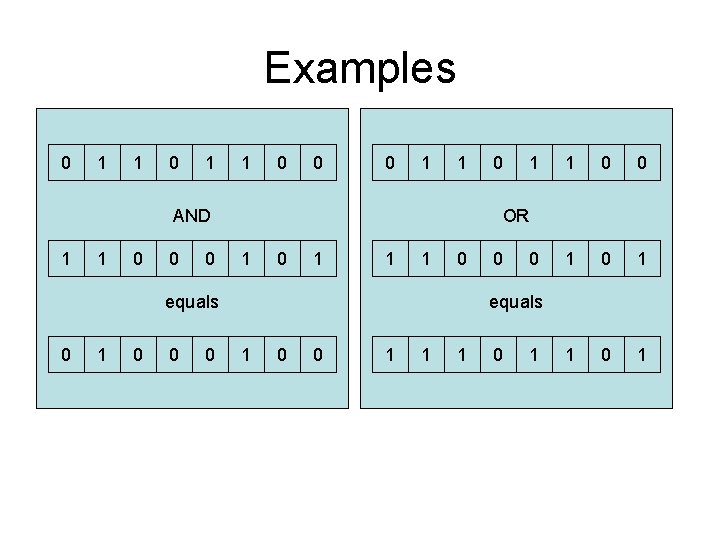
Examples 0 1 1 0 0 0 1 1 AND 1 1 0 0 0 1 1 0 1 OR 1 0 1 1 1 0 equals 0 0 equals 1 0 0 1 1 1 0 1
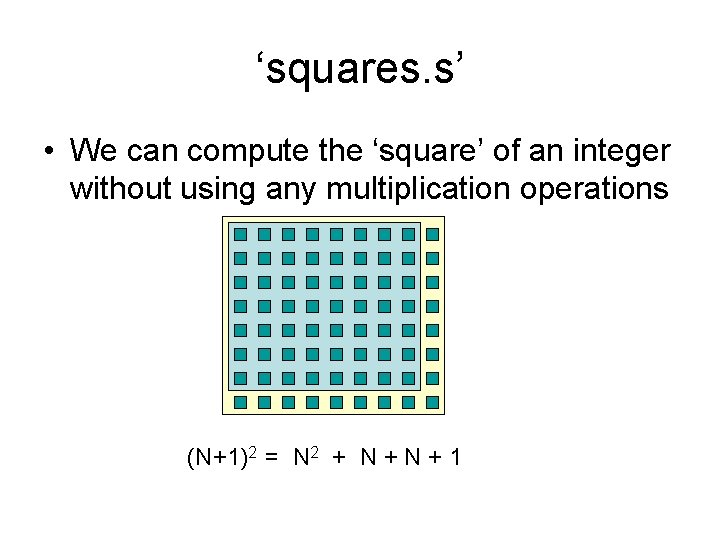
‘squares. s’ • We can compute the ‘square’ of an integer without using any multiplication operations (N+1)2 = N 2 + N + 1
- Slides: 8