Working towards the current model of the atom

Working towards the current model of the atom….

Hey everyone! How’s it going? It’s time to look at Bohr’s model of the atom!! Ya. HOOOO!

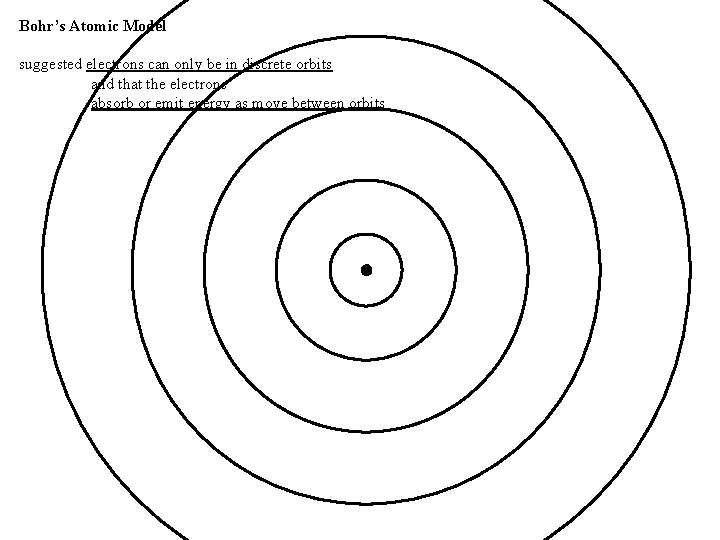
Bohr’s Atomic Model suggested electrons can only be in discrete orbits and that the electrons absorb or emit energy as move between orbits

Bohr’s Atomic Model suggested electrons can only be in discrete orbits and that the electrons absorb or emit energy as move between orbits as electrons move between orbits, the PE/KE of the electron is transformed into radiation (photon) the difference in energy between states is equal to the energy of a photon (places where the electron can be) E = Ephoton = h energy gained/lost by e- energy of photon absorbed/released

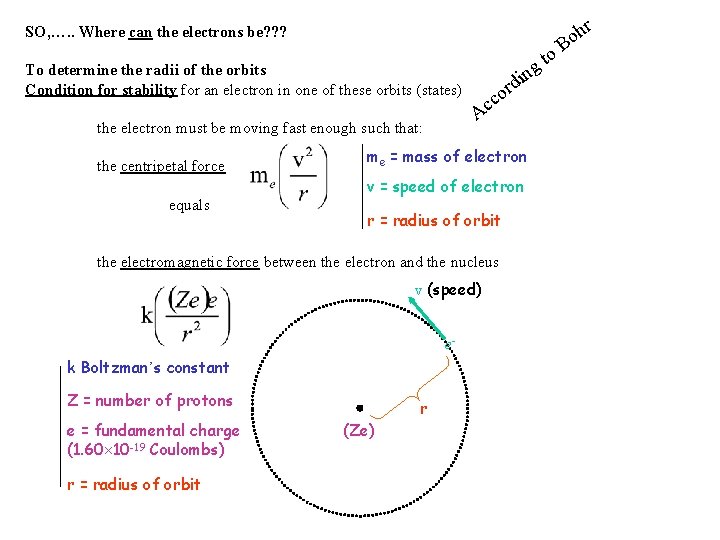
SO, …. . Where can the electrons be? ? ? To determine the radii of the orbits Condition for stability for an electron in one of these orbits (states) equals r o cc A the electron must be moving fast enough such that: the centripetal force me = mass of electron v = speed of electron r = radius of orbit the electromagnetic force between the electron and the nucleus v (speed) ek Boltzman’s constant Z = number of protons e = fundamental charge (1. 60 10 -19 Coulombs) r = radius of orbit to g din r (Ze) B r h o

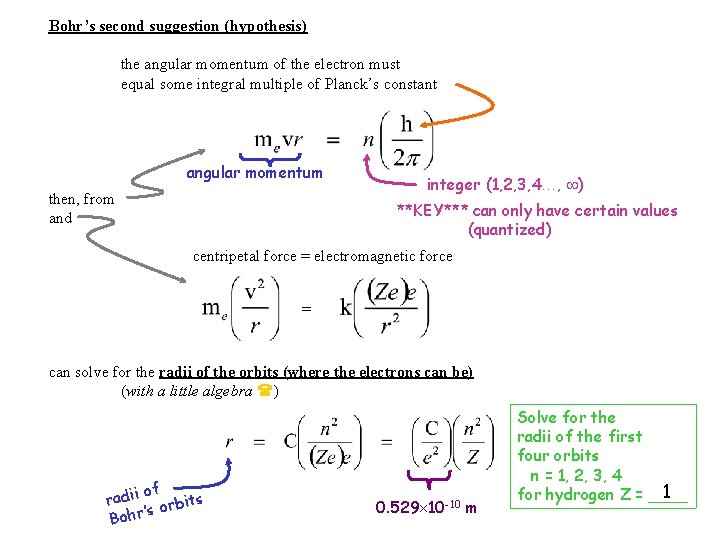
Bohr’s second suggestion (hypothesis) the angular momentum of the electron must equal some integral multiple of Planck’s constant angular momentum then, from and integer (1, 2, 3, 4…, ) **KEY*** can only have certain values (quantized) centripetal force = electromagnetic force = can solve for the radii of the orbits (where the electrons can be) (with a little algebra ) of radii orbits ’s Bohr 0. 529 10 -10 m Solve for the radii of the first four orbits n = 1, 2, 3, 4 1 for hydrogen Z = ____

Bohr’s Atomic Model of radii orbits ’s Bohr 0. 529 10 -10 m Quantized Radii 1 Hydrogen: Z = ______ For n = 1, r = 0. 529 x 10 -10 m For n = 2, r = 2. 12 x 10 -10 m For n = 3, r = 4. 76 x 10 -10 m 1. 59 10 -10 m 2. 64 10 -10 m 3. 70 10 -10 m For n = 4, r = 8. 46 x 10 -10 m. . . get further apart from each other as n increases meters !!!! For n = 4, r = ___________ - infinite number of orbits - biggest orbit is infinitely big (CURIOUS) SO, …. . why is an atom so tiny ? …… the electrons spend most of their time in orbits close to the nucleus

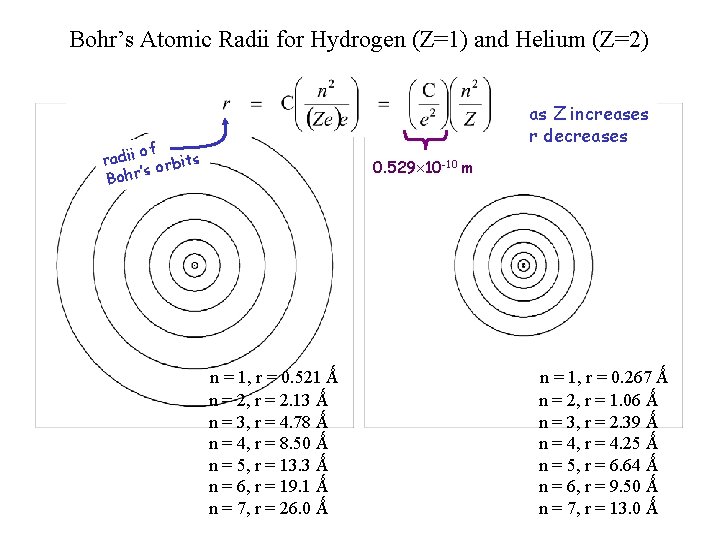
Bohr’s Atomic Radii for Hydrogen (Z=1) and Helium (Z=2) as Z increases r decreases of radii orbits ’s Bohr 0. 529 10 -10 m . . n = 1, r = 0. 521 Ǻ n = 2, r = 2. 13 Ǻ n = 3, r = 4. 78 Ǻ n = 4, r = 8. 50 Ǻ n = 5, r = 13. 3 Ǻ n = 6, r = 19. 1 Ǻ n = 7, r = 26. 0 Ǻ n = 1, r = 0. 267 Ǻ n = 2, r = 1. 06 Ǻ n = 3, r = 2. 39 Ǻ n = 4, r = 4. 25 Ǻ n = 5, r = 6. 64 Ǻ n = 6, r = 9. 50 Ǻ n = 7, r = 13. 0 Ǻ

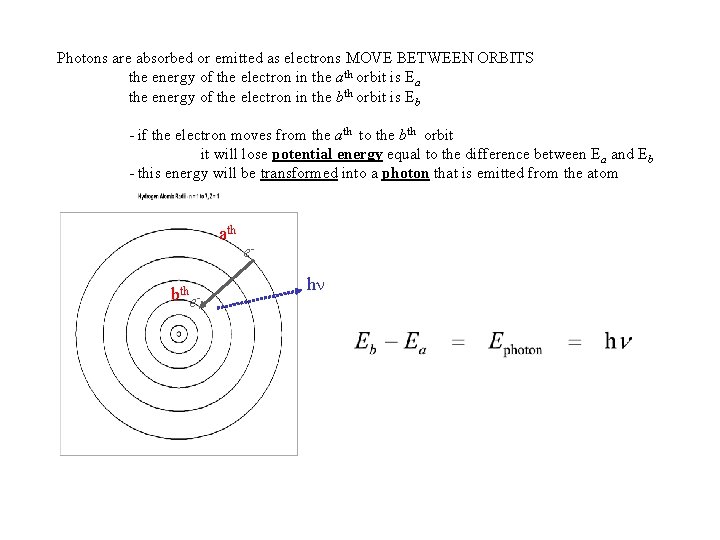
Photons are absorbed or emitted as electrons MOVE BETWEEN ORBITS the energy of the electron in the ath orbit is Ea the energy of the electron in the bth orbit is Eb - if the electron moves from the ath to the bth orbit it will lose potential energy equal to the difference between Ea and Eb - this energy will be transformed into a photon that is emitted from the atom ath bthe- eh

Bohr’s Atomic Model If the position of the e- is known, the energy of the e- in that place can be calculated Energy of an electron in a particular orbit ! ! total energy of the electron has to equal the kinetic plus potential because we don’t know how fast the e- is moving k k e e k e substitute in for velocity from balance of centripetal and electromagnetic forces e e = e e get solve for v

Quantized energy states ! ! k k The energy depends on where the electron is. If the radii are quantized, (discrete / can only be in certain places) so is the energy. (can only have certain values) e e k e e e Radii, r, are given by: Substitute in for r, and solve for the energy of an electron in a particular orbit, n: get (bunch o’ constants)

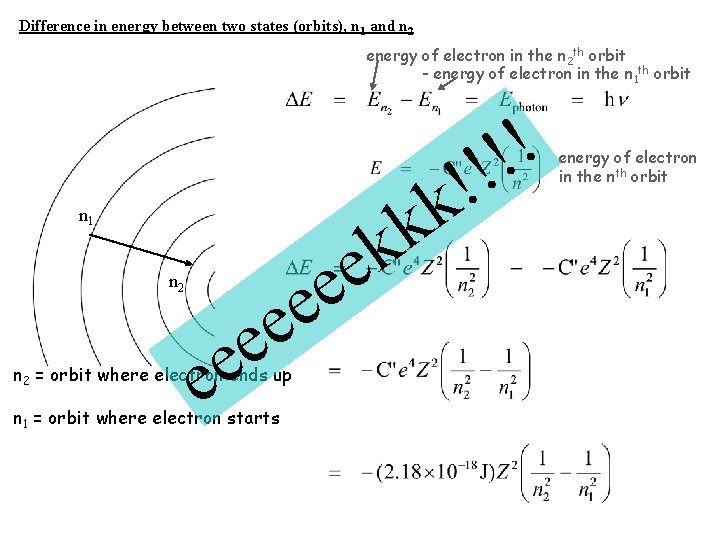
Difference in energy between two states (orbits), n 1 and n 2 energy of electron in the n 2 th orbit - energy of electron in the n 1 th orbit n 1 n 2 e e e n 2 = orbit where electron ends up n 1 = orbit where electron starts k e k k ! ! energy of electron in the nth orbit

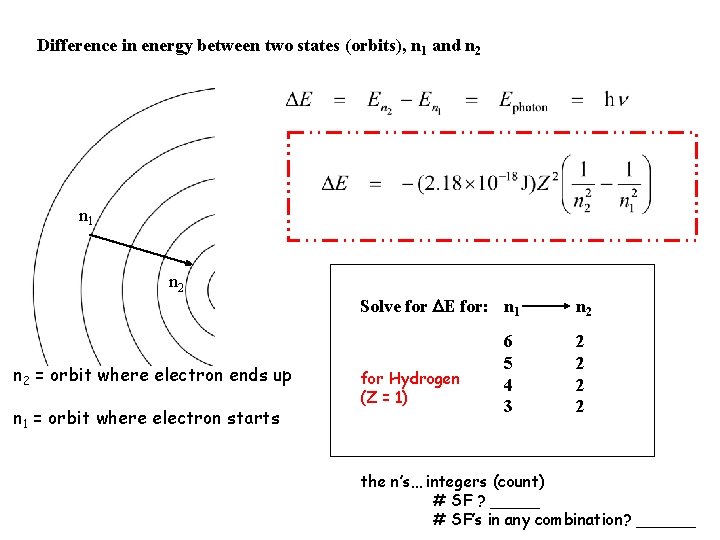
Difference in energy between two states (orbits), n 1 and n 2 n 1 n 2 = orbit where electron ends up n 1 = orbit where electron starts Solve for E for: n 1 for Hydrogen (Z = 1) 6 5 4 3 n 2 2 2 the n’s… integers (count) # SF ? _____ # SF’s in any combination? ______

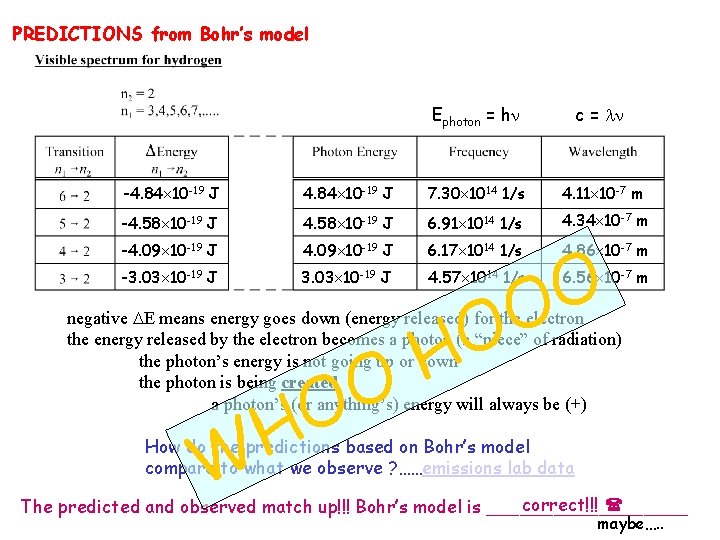
PREDICTIONS from Bohr’s model Ephoton = h c = -4. 84 10 -19 J 7. 30 1014 1/s 4. 11 10 -7 m -4. 58 10 -19 J 6. 91 1014 1/s 4. 34 10 -7 m -4. 09 10 -19 J 6. 17 1014 1/s 4. 86 10 -7 m -3. 03 10 -19 J 4. 57 1014 1/s 6. 56 10 -7 m O H O O negative E means energy goes down (energy released) for the electron the energy released by the electron becomes a photon (a “piece” of radiation) the photon’s energy is not going up or down the photon is being created a photon’s (or anything’s) energy will always be (+) W How do the predictions based on Bohr’s model compare to what we observe ? ……emissions lab data correct!!! The predicted and observed match up!!! Bohr’s model is _________ maybe…. .

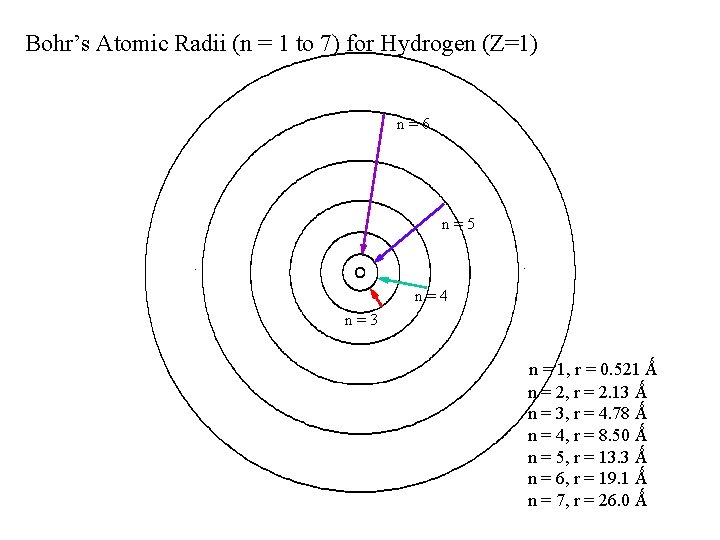
Bohr’s Atomic Radii (n = 1 to 7) for Hydrogen (Z=1) n=6 n=5. . n=4 n=3 n = 1, r = 0. 521 Ǻ n = 2, r = 2. 13 Ǻ n = 3, r = 4. 78 Ǻ n = 4, r = 8. 50 Ǻ n = 5, r = 13. 3 Ǻ n = 6, r = 19. 1 Ǻ n = 7, r = 26. 0 Ǻ

. … m iu (Z=2) l e Bohr’s Atomic Radii for Hydrogen (Z=1) and. H Helium r o f a t a d e h t t u o b a t a h W. . n = 1, r = 0. 521 Ǻ n = 2, r = 2. 13 Ǻ n = 3, r = 4. 78 Ǻ n = 4, r = 8. 50 Ǻ n = 5, r = 13. 3 Ǻ n = 6, r = 19. 1 Ǻ n = 7, r = 26. 0 Ǻ n = 1, r = 0. 267 Ǻ n = 2, r = 1. 06 Ǻ n = 3, r = 2. 39 Ǻ n = 4, r = 4. 25 Ǻ n = 5, r = 6. 64 Ǻ n = 6, r = 9. 50 Ǻ n = 7, r = 13. 0 Ǻ

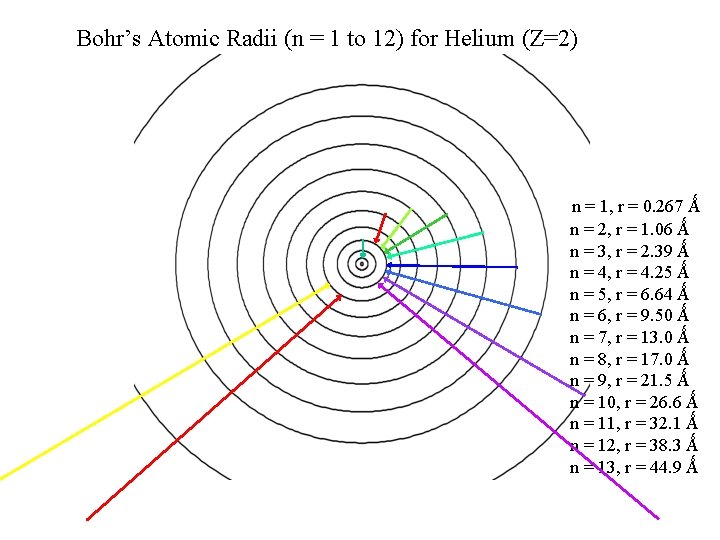
Bohr’s Atomic Radii (n = 1 to 12) for Helium (Z=2) Actual spectrum Predicted transitions in the visible. How do the predictions based on Bohr’s model compare to what we observe ? ……emissions lab data . n = 1, r = 0. 267 Ǻ n = 2, r = 1. 06 Ǻ n = 3, r = 2. 39 Ǻ n = 4, r = 4. 25 Ǻ n = 5, r = 6. 64 Ǻ n = 6, r = 9. 50 Ǻ n = 7, r = 13. 0 Ǻ n = 8, r = 17. 0 Ǻ n = 9, r = 21. 5 Ǻ n = 10, r = 26. 6 Ǻ n = 11, r = 32. 1 Ǻ n = 12, r = 38. 3 Ǻ n = 13, r = 44. 9 Ǻ

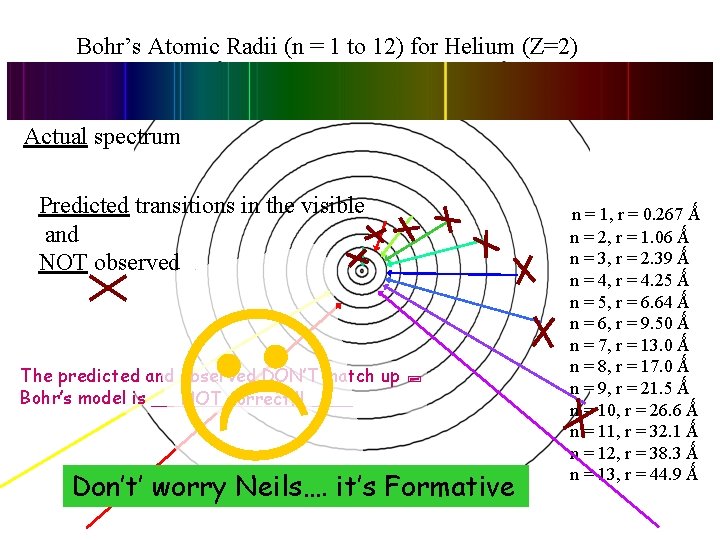
Bohr’s Atomic Radii (n = 1 to 12) for Helium (Z=2) Actual spectrum Predicted transitions in the visible and NOT observed. The predicted and observed DON’T match up Bohr’s model is _________ NOT correct!!! Don’t’ worry Neils…. it’s Formative . n = 1, r = 0. 267 Ǻ n = 2, r = 1. 06 Ǻ n = 3, r = 2. 39 Ǻ n = 4, r = 4. 25 Ǻ n = 5, r = 6. 64 Ǻ n = 6, r = 9. 50 Ǻ n = 7, r = 13. 0 Ǻ n = 8, r = 17. 0 Ǻ n = 9, r = 21. 5 Ǻ n = 10, r = 26. 6 Ǻ n = 11, r = 32. 1 Ǻ n = 12, r = 38. 3 Ǻ n = 13, r = 44. 9 Ǻ

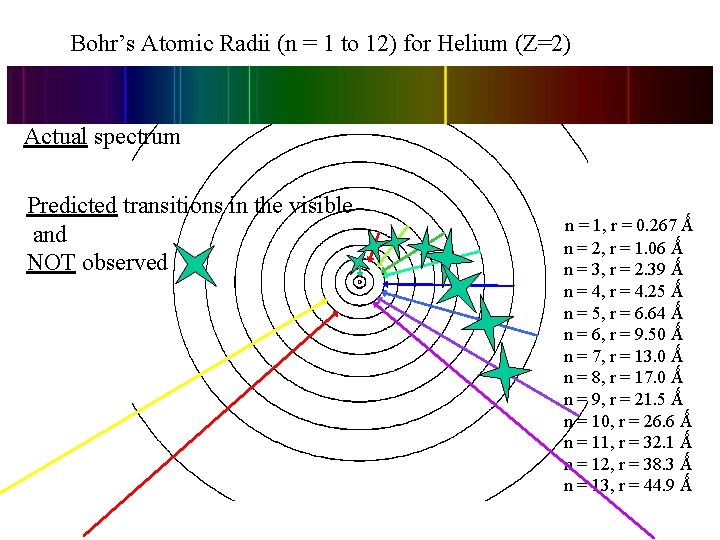
Bohr’s Atomic Radii (n = 1 to 12) for Helium (Z=2) Actual spectrum Predicted transitions in the visible and NOT observed. . n = 1, r = 0. 267 Ǻ n = 2, r = 1. 06 Ǻ n = 3, r = 2. 39 Ǻ n = 4, r = 4. 25 Ǻ n = 5, r = 6. 64 Ǻ n = 6, r = 9. 50 Ǻ n = 7, r = 13. 0 Ǻ n = 8, r = 17. 0 Ǻ n = 9, r = 21. 5 Ǻ n = 10, r = 26. 6 Ǻ n = 11, r = 32. 1 Ǻ n = 12, r = 38. 3 Ǻ n = 13, r = 44. 9 Ǻ

Bohr’s Atomic Radii (n = 1 to 12) for Helium (Z=2) n = 1, r = 0. 267 Ǻ n = 2, r = 1. 06 Ǻ n = 3, r = 2. 39 Ǻ n = 4, r = 4. 25 Ǻ n = 5, r = 6. 64 Ǻ n = 6, r = 9. 50 Ǻ n = 7, r = 13. 0 Ǻ n = 8, r = 17. 0 Ǻ n = 9, r = 21. 5 Ǻ n = 10, r = 26. 6 Ǻ n = 11, r = 32. 1 Ǻ n = 12, r = 38. 3 Ǻ n = 13, r = 44. 9 Ǻ