Work Energy and Simple Machines Physical Science Unit












































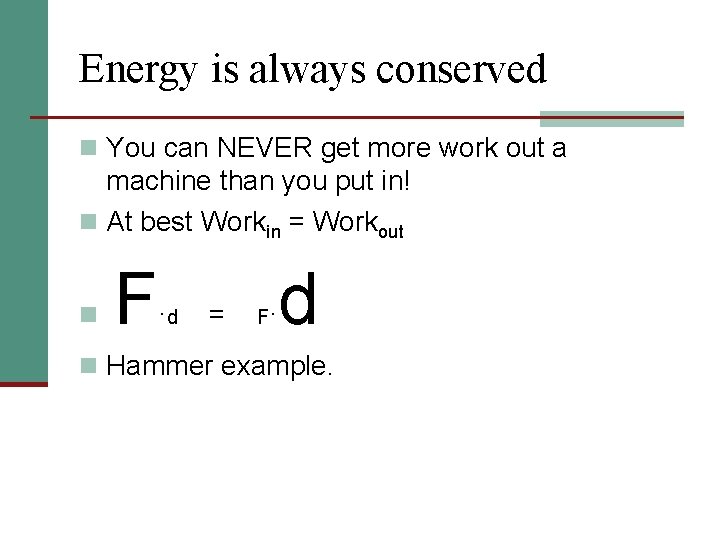
















- Slides: 63

Work, Energy and Simple Machines Physical Science: Unit 3 Chapters 4 and 5

Energy n The ability to cause change. n The “currency” of nature. n Need energy (money) to accomplish things. n Like currency, energy can be stored in different forms. n Unit of Energy n Joule (J) n kg • m²/s²

Kinetic Energy n Energy of motion. n Depends on the mass and velocity of the object. n Formula: KE= ½ m • v² n What has the greater effect, speed or mass? n

Kinetic Energy Sample Problems n What is the kinetic energy of a baseball moving at a speed of 40 m/s if the baseball has a mass of 0. 15 kg? n A car moving at 20 m/s has a kinetic energy of 300, 000 J. What is the car’s mass? n A sprinter has a mass of 80 kg and a kinetic energy of 4, 000 J. What is the sprinter’s speed?

Potential Energy n Energy of position or condition. n Gravitation P. E. n a ball above the ground. n Formula: PEg=m • g • h n Elastic Potential n Energy stored in something that can stretch or compress. n Spring wound up (as in a mousetrap) n Chemical Potential n Energy stored in chemical bonds. n Gasoline, Lunch, TNT.

Potential Energy Sample Problems n Find the height of a baseball with a mass of 0. 15 kg that has a gravitational potential energy (PEg) of 73. 5 J. n Find the PEg of Mrs. Kasch-Flugum’s coffee mug with a mass of 0. 3 kg on a 1 -meter high desk. n What is the mass of a hiker 200 m above the ground if her Peg 117, 600 J.

Forms of Energy n All forms fit under either kinetic or potential n Mechanical: n Motion or position of object. n Electrical: n Electric current- movement of electrons. n Electromagnetic: n Light- wave energy n Chemical: n Explosives and Food- changing bonds n Thermal: n Heat- movement of atoms n Nuclear: n Reactors- splitting of atoms

WS: Potential and Kinetic Energy

Energy Conversions: n Light bulb n From electrical to thermal and electromagnetic (light). n Water heater n From chemical to thermal. n Car engine n From chemical to thermal to mechanical. n Book dropped n From PE to KE to sound, and thermal.

Pendulum

Ball Toss

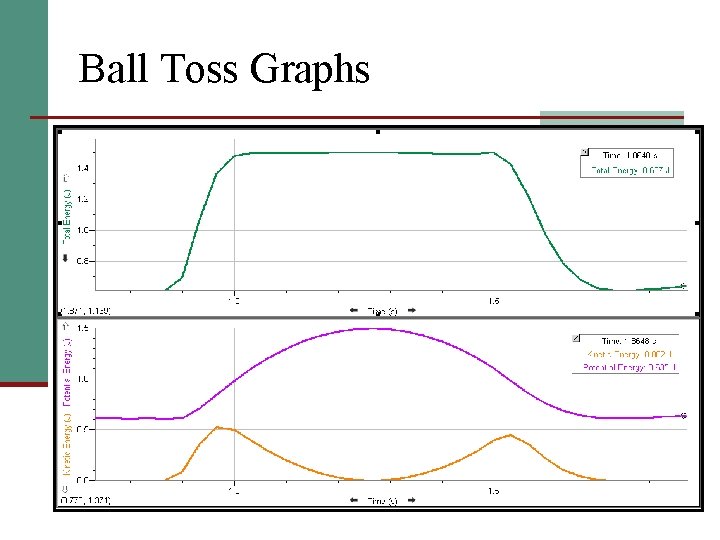
Conservation and Energy Changes n Conservation of Energy: Energy cannot be created or destroyed, but it can be transformed from one type to another. n In each transformation, some energy is misplaced. n Usually “lost” energy is in the form of thermal energy.

Lab: Energy of a Tossed Ball What happens to a ball’s KE and PE as it rises and falls?

Ball Toss Graphs

Where does the book’s energy come from? n You lifted the book, giving it energy. n Appling a force to move something is work.

Work n The transfer of energy through motion. n To have work, a force must be applied through distance. n This force must partially be in the same direction of the movement. n Work or no work done? Lifting book n Carrying book n Pushing chair n Pushing wall n

Units of Work n Work is measured in Joules or Newton – meters. n So many Joules of energy are transferred from one object to the next.

Calculating Work n To calculate work, take the force applied times the distance moved. n Work (J or N·m)= Force (N) x distance (m)

Work Sample Problem #1 n A dancer lifts a 400 N ballerina 1. 4 m overhead. How much work is done on the ballerina? Givens: n Unknown: n Formula: n Solve: n

Work Sample Problem #1 n A dancer lifts a 400 N ballerina 1. 4 m overhead. How much work is done on the ballerina? Givens: Force = 400 N; Distance = 1. 4 meters · n Unknown: Work n Formula: W=F · d n Solve: Work = 400 N · 1. 4 m = n

Work Sample Problem #1 n A dancer lifts a 400 N ballerina 1. 4 m overhead. How much work is done on the ballerina? Givens: Force = 400 N; Distance = 1. 4 meters · n Unknown: Work n Formula: W=F · d n Solve: Work = 400 N · 1. 4 m = 560 Joules n

Work Sample Problem #2 n A carpenter lifts a 45 kg beam 1. 2 m. How much work is done on the beam? Givens: n Unknown: n Formula: n Solve: n

Work Sample Problem #2 n A carpenter lifts a 45 kg beam 1. 2 m. How much work is done on the beam? Givens: mass = 45 kg; distance = 1. 2 m n Unknown: Work n Formula: Work = F · d n Solve: 45 kg is not a force!! So. . . n

Work Sample Problem #2 n A carpenter lifts a 45 kg beam 1. 2 m. How much work is done on the beam? Givens: mass = 45 kg; distance = 1. 2 m n Unknown: Work n Formula: Work = F · d; F (weight) = m · 9. 8 n Solve: F= 45 kg · 9. 8 = 441 N Work = 441 N · 1. 2 m = n

Work Sample Problem #2 n A carpenter lifts a 45 kg beam 1. 2 m. How much work is done on the beam? Givens: mass = 45 kg; distance = 1. 2 m n Unknown: Work n Formula: Work = F · d; F (weight) = m · 9. 8 n Solve: F= 45 kg · 9. 8 = 441 N Work = 441 N · 1. 2 m = 529. 2 J n

Work Sample Problem #3 n The carpenter then carries the beam 10 m. How much work is done on the beam? n n Givens: Unknown: Formula: Solve:

Work Sample Problem #3 n The carpenter then carries the beam 10 m. How much work is done on the beam? n n Givens: Is the force in the same direction as your movement? Unknown: Formula: Solve:

Work Sample Problem #3 n The carpenter then carries the beam 10 m. How much work is done on the beam? n Givens: Is the force in the same direction as your movement? NO! So there is no work done!!

Power n A science teacher and a weight lifter both lift 100 pounds. Who does more work? n Who can do it quicker? n Who has more power? n

Power n A science teacher and a weight lifter both lift 100 pounds. Who does more work? Same Work n Who can do it quicker? Weight Lifter n Who has more power? Weight Lifter n n Power is the amount of work done in a unit of time. n Unit of power is Joules per second which is a watt. (W)

Calculating Power n Power is the amount work done divided by time it took. n Power (Watts) = Work (J) / time (s)

Power Practice Problem #1 n An athlete lifting weights does 900 J of work in 2 seconds. What is the athlete’s power? Givens: n Unknown: n Formula: n Solve: n

Power Practice Problem #1 n An athlete lifting weights does 900 J of work in 2 seconds. What is the athlete’s power? Givens: Work = 900 J; time = 2 seconds n Unknown: Power n Formula: Power = work / time n Solve: n

Power Practice Problem #1 n An athlete lifting weights does 900 J of work in 2 seconds. What is the athlete’s power? Givens: Work = 900 J; time = 2 seconds n Unknown: Power n Formula: Power = work / time n Solve: P = 900 J / 2 s = n

Power Practice Problem #1 n An athlete lifting weights does 900 J of work in 2 seconds. What is the athlete’s power? Givens: Work = 900 J; time = 2 seconds n Unknown: Power n Formula: Power = work / time n Solve: P = 900 J / 2 s = 450 Watts n

Power Practice Problem #2 n You use force of 10 N to move a box 100 m in 10 sec. Watts your power? Givens: n Unknown: n Formula: n Solve: n

Power Practice Problem #2 n You use force of 10 N to move a box 100 m in 10 sec. What is your power? Givens: F = 10 N; d = 100 m; t = 10 s n Unknown: Power n Formula: P = W/t; W=F·d n Solve: n

Power Practice Problem #2 n You use force of 10 N to move a box 100 m in 10 sec. What is your power? Givens: F = 10 N; d = 100 m; t = 10 s n Unknown: Power n Formula: P = W/t; W=F·d n Solve: W= 10 N · 100 m = 1000 J P= ? n

Power Practice Problem #2 n You use force of 10 N to move a box 100 m in 10 sec. What is your power? Givens: F = 10 N; d = 100 m; t = 10 s n Unknown: Power n Formula: P = W/t; W=F·d n Solve: W= 10 N · 100 m = 1000 J P= 1000 J / 10 s = 100 Watts n

Power Practice Problem #3 n A light bulb is rated 60 Watts. How many Joules of energy are used by this light bulb in an hour? Givens: n Unknown: n Formula: n Solve: n

Power Practice Problem #3 n A light bulb is rated 60 Watts. How many Joules of energy are used by this light bulb in an hour? Givens: Power = 60 W; t = 3600 s n Unknown: Joules n Formula: P = W/t ; W = P·t n Solve: n

Power Practice Problem #3 n A light bulb is rated 60 Watts. How many Joules of energy are used by this light bulb in an hour? Givens: Power = 60 W; t = 3600 s n Unknown: Joules n Formula: P = W/t ; W = P·t n Solve: W = 60 W · 3600 s = 216, 000 J n

KE, PE, Work and Power Worksheet #1

Machines n Machines manipulate energy by adjusting how the work is done. n A machine can…. . Change the direction of a force (pulley) n Change the output force (lever) n Change the distance the force works (baseball bat) n n A machine will never increase both the force and distance at the same time. n You trade one for the other.

How a machine works n You do work on the machine n Work input (Win) n The machine takes that work, changes it, and does work on an object n Work output (Wout)
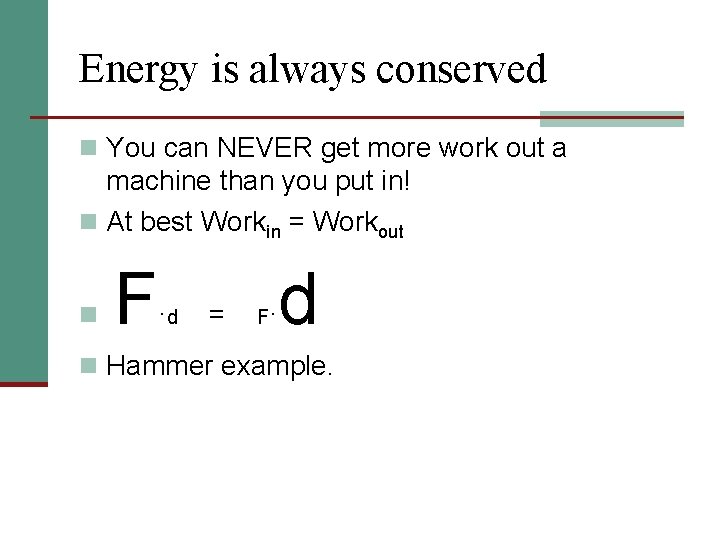
Energy is always conserved n You can NEVER get more work out a machine than you put in! n At best Workin = Workout n F ·d = F· d n Hammer example.

Mechanical Advantage n Number of times a machine multiplies the force you put in. n Output Force / Input Force n If the distance is multiplied, output force is less then input force. MA is a decimal. n If direction is changed (opposite), MA=1

Efficiency of Machines n Compares work put in to the work you get out. n A percentage- higher is better. n 100% is an ideal machine n Efficiency = Output Work / Input Work n No machine is 100% efficient. Some energy is always lost in friction.

Incline Plane n A sloping surface used to raise objects. n IMA = length of slope / height of slope n Usually has a low efficiency. n Examples: n Ramp n Staircase

Levers n A bar that is free to pivot, or turn, about a fixed point. Fulcrum: the fixed point of a lever. n Effort arm: From fulcrum to where you push. n Resistance arm: From the fulcrum to where object (resistance) is. n n Ideal Mechanical Advantage = length of the effort arm / length of the resistance arm

Classes of Levers n There are three different types or classes of levers.

1 st Class Lever n Effort, Fulcrum, Resistance

1 st Class Lever - Examples n Examples: n Pry Bar n “Claw” on hammer n Two wheeled cart

2 nd Class Lever n Fulcrum, Resistance, Effort

2 nd Class Lever - Examples n Examples: n Wheelbarrow n Nut Cracker

3 rd Class Lever n Fulcrum, Effort, Resistance n Do not increase force, but distance.

3 rd Class Lever - Examples n Broom n Baseball bat n Mouse trap

Key Point! All machines are variation of the incline plane or lever.

Wheel and Axle n Definition: Two wheels of different sizes that rotate together. n Examples: Steering wheels n Gears n Chain on bikes n n IMA = radius of wheel (you) / radius of axle (machine)

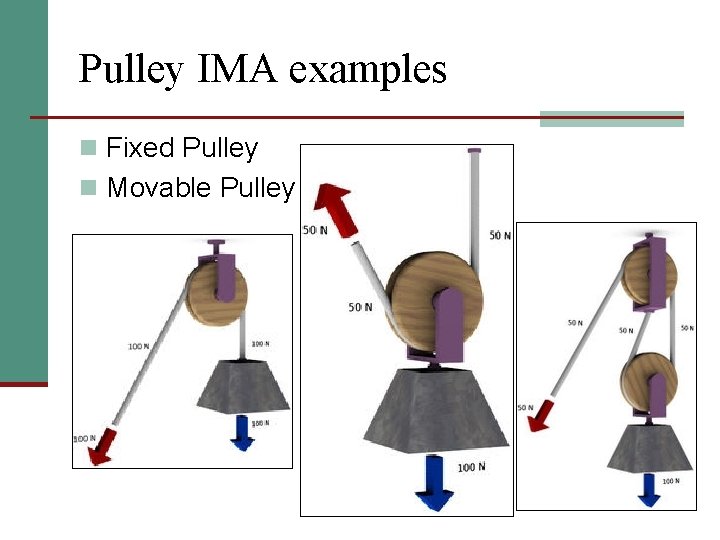
Pulley n Definition: A grooved wheel with a rope or a chain along the groove. n Pulleys can be fixed or movable. n IMA of fixed pulley is equal to 1. n The IMA of a movable pulley is equal to the number of ropes that support the resistance weight.

Pulley IMA examples n Fixed Pulley n Movable Pulley

Wedge n An inclined plane with one or two sloping sides.

Screw n An incline plane wrapped in a spiral around a post.