Work Do Now What do you think it

Work Do Now What do you think it means to do work? You carry something across the room without changing its height. Did you do work? You push all day on a wall just for fun and it never moves. Did you do work? Why do we use ramps and pulleys?

Work W=Fx This formula applies when: • the force is constant • the force is in the same direction as the displacement of the object F x

Work Example A 50 N horizontal force is applied to a 15 kg crate over a distance of 10 m. The amount of work this force does is: Tofu Almond Crunch 50 N 10 m

Work Example A 50 N horizontal force is applied to a 15 kg crate over a distance of 10 m. The amount of work this force does is: W = 50 N · 10 m = 500 N · m Tofu Almond Crunch 50 N 10 m

Work Example W = 50 N · 10 m = 500 N · m The SI unit of work is the Newton · meter. This is also called the Joule, J. 1 Joule = 1 Newton · meter, Tofu Almond Crunch 50 N 10 m

Negative Work Forces acting opposite the direction of motion does (-) work. Suppose a box skids across the floor until friction stops it. The displacement is to the right, but the force of friction left. What is the frictional work in this case? v Tofu Almond Crunch fk = 20 N 7 m

Negative Work Forces acting opposite the direction of motion does (-) work. Suppose a box skids across the floor until friction stops it. The displacement is to the right, but the force of friction left. W=Fd= (-20)(7) = -140 J. v Tofu Almond Crunch fk = 20 N 7 m

When zero work is done As the crate slides horizontally, the normal force and weight do no work at all, because they are perpendicular to the displacement. N Tofu Almond Crunch mg 7 m

When zero work is done If the granola bar were moving vertically, such as in an elevator, then they each force would be doing work. Moving up in an elevator the normal force would do positive work, and the weight would do negative work. N Tofu Almond Crunch mg 7 m

When zero work is done Another case when zero work is done is with zero displacement. Even though the force applied is 200 lb, and work was done in getting over head, no work is done just holding it over head.

Net Work The net work done on an object is the sum of all the work done on it. Work is a scalar, so we can simply add work up. The applied force does +200 J of work; friction does -80 J of work; and the normal force and weight do zero work. So, Wnet = 200 J - 80 J + 0 = 120 J Note that (Fnet ) (distance) = (30 N) (4 m) = 120 J. Therefore, Wnet = Fnet x N Tofu Almond Crunch fk = 20 N mg FA = 50 N 4 m

When the force is at an angle The component of F parallel to the displacement does work, The perpendicular component of F does zero work. W = F x cos F sin Tofu Almond Crunch F F cos x This formula assumes that F is constant.

Work: Incline First we break F into components and // to the ramp. F = Fn= Fg cos ( ) Only forces // to the ramp do any work. Ffk = Fn k F// = Fg sin ( ) m d Fg=mg

Work: Incline First we break F into components and // to the ramp. Then we multiply the F// by the distance the block travels. F = Fn= Fg cos ( ) Only forces // to the ramp do any work. Ffk = Fn k F// = Fg sin ( ) m d Fg=mg

Forms of Energy When work is done on an object, the amount of energy it has changes. The types of energy it possesses could also change. Here are some types of energy you should know: • Kinetic energy • Rotational Kinetic Energy • Gravitational Potential Energy • Elastic Potential Energy • Chemical Potential Energy • Mass itself • Electrical energy • Light • Sound • Other waves • Thermal energy

Kinetic Energy Kinetic energy is the energy of motion. By definition, kinetic energy is given by: K = ½ mv 2 The equation shows that. . . • the more mass a body has • or the faster it’s moving. . . the more kinetic energy it has.

Kinetic Energy Kinetic energy is the energy of motion. By definition, kinetic energy is given by: K = ½ mv 2 The equation shows that. . . • the more mass a body has • or the faster it’s moving. . . the more kinetic energy it has K is proportional to v 2, so doubling the speed quadruples kinetic energy, and tripling the speed makes it nine times greater.

Energy Units The formula for kinetic energy, K = ½ m v 2, shows that its units are: kg · (m/s)2 = kg · m 2 / s 2 = (kg · m / s 2 ) m = N·m = J So the SI unit for kinetic energy is the Joule, just as it is for work. The Joule is the SI unit for all types of energy.

Another Type of Energy Another type of energy that you know about is the calorie. This is the energy to heat up 1 gram of water 1 degree Co 1 cal = 4. 186 J A food calorie is really a kilocalorie. 1 Cal = 1000 cal = 4186 J

Kinetic Energy Example A 55 kg toy sailboat is cruising at 3 m/s. What is its kinetic energy? Note: Kinetic energy (along with every other type of energy) is a scalar, not a vector!

Kinetic Energy Example A 55 kg toy sailboat is cruising at 3 m/s. What is its kinetic energy? This is a simple plug and chug problem: K = 0. 5 (55) (3) 2 = 247. 5 J Note: Kinetic energy (along with every other type of energy) is a scalar, not a vector!

Work - Energy Theorem: The net work done on an object equals its change in energy. If the work is being used to change an object’s speed then: Wnet = = Kf - K 0 = K

Work - Energy Sample 1 Bobby takes his 1800 kg pet rhinoceros, Gertrude, ice skating. Gertrude coasts at 4 m/s and is slowed down because of friction. The force of friction is 170 N. How fast is she going after 25 meters?

Work - Energy Sample 1 Bobby takes his 1800 kg pet rhinoceros, Gertrude, ice skating. Gertrude coasts at 4 m/s and is slowed down because of friction. The force of friction is 170 N. How fast is she going after 25 meters? The force is negative since it is opposing motion Wnet = (-170 N) (25 m) = -4250 J By the work-energy theorem this is the change in her kinetic energy, meaning she loses this much energy. Thus, -4250 J = K = ½ m vf 2 - ½ m v 02 = ½ m (vf 2 - v 02) = ½ (1800 kg) [vf 2 - (4 m/s)2] vf = 3. 358 m/s

Gravitational Potential Energy Objects above the Earth’s ground have energy by virtue of their height. This is gravitational potential energy. If allowed to fall, the energy can be converted into other forms like kinetic energy, heat, and sound. U = mgh The equation shows that. . . • the more mass a body has • or the stronger the gravitational field it’s in • or the higher up it is. . . the more gravitational potential energy it’s got.

SI Potential Energy Units From the equation U = m g h the units of gravitational potential energy must be: kg · (m/s 2) · m = (kg · m/s 2) · m = N · m = J This shows the SI unit for potential energy is the Joule, as it is for work and all other types of energy.

Reference point for U is arbitrary Gravitational potential energy depends on an object’s height, It doesn’t matter what we choose as a reference point so long as we are consistent. continued on next slide

Reference point for U is arbitrary Example: A 190 kg mountain goat is perched precariously atop a 220 m mountain ledge. How much gravitational potential energy does it have? continued on next slide

Reference point for U is arbitrary Example: A 190 kg mountain goat is perched precariously atop a 220 m mountain ledge. How much gravitational potential energy does it have? U = mgh = (190 kg) (9. 8 m/s^2) (220 m) = 409, 640 J This is how much energy the goat has with respect to the ground. It would be different if we had chosen a different reference point. continued on next slide

Work and Potential Energy FA = 10 N mg = 10 N If a force does work on an object but does not increase its kinetic energy, then that work is converted into some other form of energy, such as potential energy or heat.

Work and Potential Energy FA = 10 N mg = 10 N Suppose a 10 N upward force is applied to our miniwatermelon over a distance of 5 m. Since its weight is 10 N, the net force on it is zero, so there is no net work done on it. The work-energy theorem says that the melon undergoes no change in kinetic energy. However, it does gain gravitational potential energy in the amount of U = mgh = (10 N) (5 m) = 50 J. Notice that this is the same amount of work that the applied force does on it: W = F d = (10 N) (5 m) = 50 J. This is an example of the conservation of energy.

Conservation of Energy One of the most important principles in all of science is conservation of energy. It is also known as the first law of thermodynamics. It states that energy can change forms, but it cannot be created or destroyed. This means that all the energy in a system before some event must be accounted for afterwards. before m For example, suppose a mass is dropped from some height. The gravitational potential energy it had originally is not destroyed. Rather it is converted into kinetic energy and heat. (The heat is generated due to heat friction with the air. ) The initial total energy is given by E 0 = U = mgh. The final total energy is given by Ef = K + heat = ½ mv 2 + heat. Conservation of after energy demands that E 0 = Ef. m Therefore, mgh = ½ m v 2 + heat. v

Conservation of Energy vs. Kinematics Many problems that we’ve been solving with kinematics can be solved using energy methods. For many problems energy methods are easier, and for some it is the only possible way to solve them. Let’s do one both ways: A 185 kg orangutan drops from a 7 m high branch in a rainforest in Indonesia. How fast is he moving when he hits the ground? kinematics: Conservation of energy: vf 2 - v 02 = 2 a x vf 2 = 2 (-9. 8) (-7) vf = 11. 71 m/s E 0 = Ef mgh = ½ mv 2 2 gh = v 2 v = [2 (9. 8) (7)] ½ = 11. 71 m/s Note: the mass didn’t matter in either method. Also, we ignored air resistance in each, meaning a is a constant in the kinematics method and no heat is generated in the energy method.

Waste Heat The thermal energy that is converted from other forms due to friction, air resistance, drag, etc. is often referred to as “waste heat” because it represents energy “robbed from the system. ” In real life some of the potential energy the orangutan had in the last example would have been converted to waste heat, making his fur and the surrounding air a tad bit hotter. This means that the ape has less kinetic energy upon impact than he had potential energy up in the tree. Air resistance robbed him of energy, but all the energy is still account for. What happens to all his energy after he drops and is just standing still on the ground? (Now he has no kinetic or potential energy. ) answer: It all ends up as waste heat. A small amount of energy is carried off as sound, but that eventually ends up as waste heat as well.

Incline / friction example A crate slides down a ramp. Use energy methods to find its speed at the bottom of the ramp. Acme k = 0. 21 4 m 18 m continued on next slide

Incline / friction example A crate slides down a ramp. Use energy methods to find its speed at the bottom of the ramp. answer: The grav. potential energy at the top is partly converted to kinetic energy. Friction turns the rest into waste heat. The work that friction does is negative. Acme k = 0. 21 4 m 18 m continued on next slide

Incline / friction example (cont. ) Let h = height of ramp; = angle of inclination; d = length of ramp. E 0 = Ef Acme k = 0. 21 4 m 18 m U = | Wf | + K

Incline / friction example (cont. ) Let h = height of ramp; = angle of inclination; d = length of ramp. E 0 = Ef U = | Wf | + K m g h = Fkf d + ½ m v 2 = ( km g cos ) d + ½ m v 2 Acme k = 0. 21 4 m 18 m

Incline / friction example (cont. ) Let h = height of ramp; = angle of inclination; d = length of ramp. E 0 = Ef U = | Wf | + K m g h = Fkf d + ½ m v 2 = ( km g cos ) d + ½ m v 2 g h = k g (18 / d ) d + ½ v 2 = k g (18) + ½ v 2 Acme k = 0. 21 4 m 18 m

Incline / friction example (cont. ) Let h = height of ramp; = angle of inclination; d = length of ramp. E 0 = Ef U = | Wf | + K m g h = Fkf d + ½ m v 2 = ( km g cos ) d + ½ m v 2 g h = k g (18 / d ) d + ½ v 2 = k g (18) + ½ v 2 v = [ 2 g h - 36 k g ] ½ = [ 19. 6 (4) - 36 (0. 21) (9. 8) ] ½ v = 2. 07 m/s Acme k = 0. 21 4 m 18 m Note that we never actually had to calculate d or .

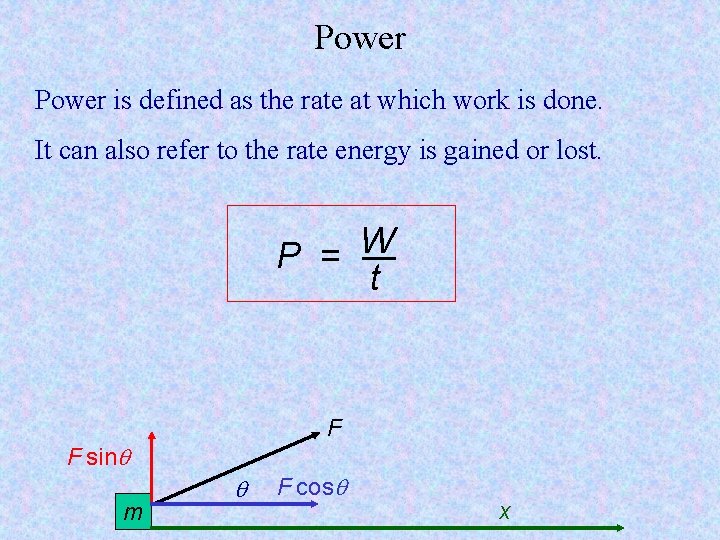
Power is defined as the rate at which work is done. It can also refer to the rate energy is gained or lost. W P = t F F sin m F cos x

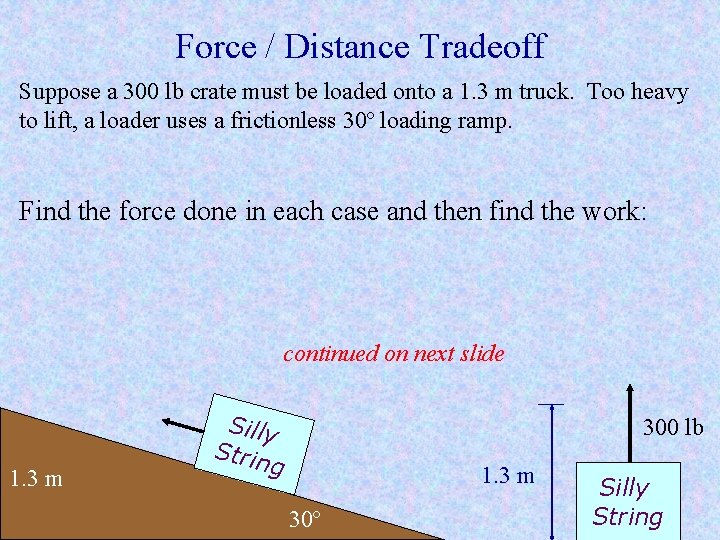
Force / Distance Tradeoff Suppose a 300 lb crate must be loaded onto a 1. 3 m truck. Too heavy to lift, a loader uses a frictionless 30º loading ramp. Find the force done in each case and then find the work: continued on next slide 1. 3 m Silly Strin g 300 lb 1. 3 m 30º Silly String

Force / Distance Tradeoff Suppose a 300 lb crate must be loaded onto a 1. 3 m truck. Too heavy to lift, a loader uses a frictionless 30º loading ramp. With the ramp, the worker only needs a 150 lb force (sin 30º = ½). A little trig gives us the length of the ramp: 2. 6 m. With the ramp, the worker applies half the force over twice the distance. In either case the work done is the same! 150 lb 1. 3 m Silly Strin g 300 lb 1. 3 m 30º Silly String

Force / Distance Tradeoff (cont. ) So why does the truck loader bother with the ramp if he does as much work with it as without it? In fact, if the ramp were not frictionless, he would have done even more work with the ramp than without it.

Force / Distance Tradeoff (cont. ) So why does the truck loader bother with the ramp if he does as much work with it as without it? In fact, if the ramp were not frictionless, he would have done even more work with the ramp than without it. answer: Even though the work is the same or more, he simply could not lift a 300 lb box straight up on his own. The simple machine allowed him to apply a lesser force over a greater distance. This is the “force / distance tradeoff. ”

Force / Distance Tradeoff (cont. ) A simple machine allows a job to be done with a smaller force, but the distance over which the force is applied is greater. In a frictionless case, the product of force and distance (work) is the same with or without the machine.

Mechanical Advantage Mechanical advantage is the ratio of the amount of force that must be applied to do a job with a machine to the force that would be required without the machine. Fout M. A. = Fin What was the ramps mechanical advantage in the last problem? Note: a mechanical advantage has no units and is typically > 1.

Mechanical Advantage With the ramp the worker only had to push with a 150 lb force. His input force was 150 lb. The effective output force which is what he would have had to apply without the ramp was 300 lb. Fout M. A. = Fin Therefore, the mechanical advantage of this particular ramp is M. A. = (300 lb) / (150 lb) = 2. Note: a mechanical advantage has no units and is typically > 1.

Work - Energy Theorem Darivation: The net work done on an object equals its change in energy. Here’s a proof when Fnet is in line with the displacement, x. Recall that for uniform acceleration, average speed = v = ½ (vf + v 0 ). Wnet = Fnet x = m a x = m x ( v / t ) = m (x / t) v = m v (vf - v 0) = m [ ½ (vf + v 0)] (vf - v 0) = ½ m (vf 2 - v 02) = ½ m vf 2 - ½ m v 02 = Kf - K 0 = K