Work and Energy Dr Walker Work Work is

Work and Energy Dr. Walker

Work • Work is the product of the force on an object and the distance through which the object is moved: the quantity force × distance • When we lift an object against gravity, we perform work • Work is increased when – We lift something heavier (F = ma) – We accelerate an object at a higher rate (F = ma) – We move something farther (W = Fd)

Work Units • The unit of measurement for work combines a unit of force, N, with a unit of distance, m. • The unit of work is the newton-meter (N • m), also called the joule. • Remember, W = Fd • One joule (J) of work is done when a force of 1 N is exerted over a distance of 1 m (lifting an apple over your head).

Examples of Work • An archer stretches her bowstring, doing work against the elastic forces of the bow. • When the ram of a pile driver is raised, work is required to raise the ram against the force of gravity. • When you do push-ups, you do work against your own weight. • Bringing an automobile up to speed or in slowing it down involves work.

Example 1 • Suppose that you apply a 60 -N horizontal force to a 32 -kg package, which pushes it 4 meters across a mailroom floor. How much work do you do on the package?

Example 1 • Suppose that you apply a 60 -N horizontal force to a 32 -kg package, which pushes it 4 meters across a mailroom floor. How much work do you do on the package? • W = Fd = 60 N x 4 m = 240 J – Notice we didn’t need the mass (tricksy hobbitses…)

Example 2 • A 6600 kg building is moved a distance of 2. 5 m. What is the amount of work performed?

Example 2 • A 6600 kg building is moved a distance of 2. 5 m. What is the amount of work performed? • What is the force of the building? – F = ma = (6600 kg)(9. 8 m/s 2) = 6. 5 x 104 N • What is the work? – W = Fd = (6. 5 x 104 N)(2. 5 m) = 1. 6 x 105 J

Example 3 • A lifter performs a 440 lb (200 kg) deadlift. The distance from the floor to lockout is 0. 6 m. How much work is performed?

Example 3 • A lifter performs a 440 lb (200 kg) deadlift. The distance from the floor to lockout is 0. 6 m. How much work is performed? • W = Fd • W = (ma)d • W = (200 kg)(9. 8 m/s 2)(0. 6 m) = 1179 J or 1. 18 k. J

Energy • The ability to produce change within a system – Potential Energy (“position”) • Elastic potential energy (an extended rubber band) • Chemical energy (stored in chemical bonds, released during reactions) • Gravitational potential energy (released during a fall) – Kinetic Energy (“motion)

Gravitational Potential Energy • The amount of gravitational potential energy possessed by an elevated object is equal to the work done against gravity to lift it. – The upward force of a stationary object is mass x acceleration due to gravity – W = Fd • As a result, for gravitational potential energy, it’s PE = mgh or mass x gravity x height

Example 1 • What is the potential energy of a 10 kg boulder at a height of 2 m?

Example 1 • What is the potential energy of a 10 kg boulder at a height of 2 m? • PE = mgh • PE = (10 kg)(9. 8 m/s 2)(2 m) = 196 J

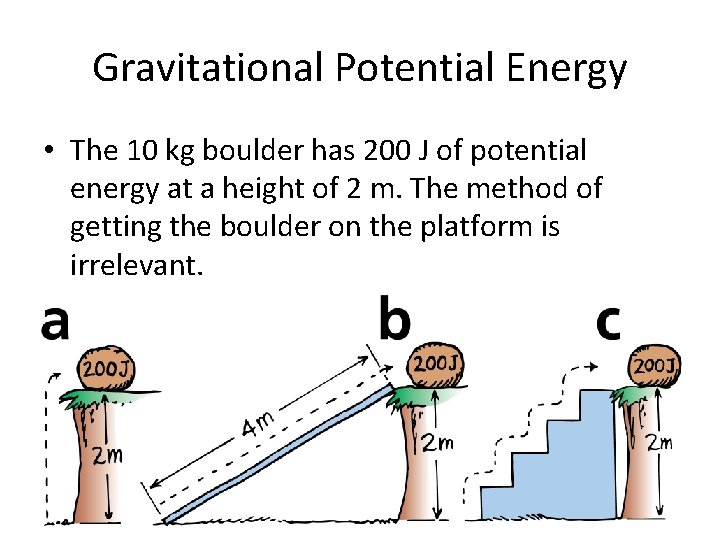
Gravitational Potential Energy • The 10 kg boulder has 200 J of potential energy at a height of 2 m. The method of getting the boulder on the platform is irrelevant.

Example 2 • A cart is loaded with a brick and pulled at constant speed along an inclined plane to the height of a seat-top. If the mass of the loaded cart is 3. 0 kg and the height of the seat top is 0. 45 meters, then what is the potential energy of the loaded cart at the height of the seattop?

Example 2 • A cart is loaded with a brick and pulled at constant speed along an inclined plane to the height of a seat-top. If the mass of the loaded cart is 3. 0 kg and the height of the seat top is 0. 45 meters, then what is the potential energy of the loaded cart at the height of the seat-top? • PE = mgh • PE = (3. 0 kg)(9. 8 m/s 2)(0. 45 m) = 13. 2 J – Note: If you were asked for the work performed, you would’ve done the same calculation since mg = F and the height is the distance

Kinetic Energy • Energy of Motion • KE = ½ mv 2 – If the velocity is doubled, the KE increases by a factor of 4 • This can be derived W = Fd, F = ma, and Vf = Vi + 2 ad

Kinetic Energy Example 1 • Determine the kinetic energy of a 625 -kg roller coaster car that is moving with a speed of 18. 3 m/s.

Kinetic Energy Example 1 • Determine the kinetic energy of a 625 -kg roller coaster car that is moving with a speed of 18. 3 m/s. • KE = ½ mv 2 • KE = ½(625 kg)(18. 3 m/s)2 = 105000 J = 105 k. J

Kinetic Energy Example 2 • Missy Diwater, the former platform diver for the Ringling Brother's Circus, had a kinetic energy of 12 000 J just prior to hitting the bucket of water. If Missy's mass is 40 kg, then what is her speed?

Kinetic Energy Example 2 • Missy Diwater, the former platform diver for the Ringling Brother's Circus, had a kinetic energy of 12 000 J just prior to hitting the bucket of water. If Missy's mass is 40 kg, then what is her speed? • KE = ½ mv 2 • 12000 J = ½ (40 kg)v 2 • V = 24. 5 m/s

Review Exercise • If Missy was moving at 24. 5 m/s when hitting the water, at what height was her platform?

Review Exercise • If Missy was moving at 24. 5 m/s when hitting the water, at what height was her platform? • V = at – 24. 5 m/s = (9. 8 m/s 2)t – t = 2. 5 s • D = 1/2 gt 2 – D = ½ (9. 8 m/s 2)(2. 5 s)2 – D = 30. 6 m – Or you could have used Vf 2 = Vi 2 + 2 ad and gotten the same answer.

Work-Energy Theorem • Work = ∆KE • The work is based on net work (yep, it’s a vector), which is based on the net force – Net force matters when two forces oppose each other, such as when friction is present • Work = DKE • Fd = ½mv 2 – Note: This is the “maximum” speed of a system. In free fall, this is the velocity just prior to impact.

Conservation Of Energy • The energy of an isolated system is constant over time – Energy can be converted to other forms (i. e. , potential to kinetic) – It cannot be created or destroyed – Not all energy is instantly “converted” from PE to KE. Total energy = KE + PE. The numbers below are “maximum” numbers.

Back To Missy… • Missy Diwater, the former platform diver for the Ringling Brother's Circus, had a kinetic energy of 12 000 J just prior to hitting the bucket of water. If Missy's mass is 40 kg, then how high was her platform? • Note: Yes, we already figured this out…. but how can we determine it from this information since we don’t have her speed here?

Back To Missy… • Missy Diwater, the former platform diver for the Ringling Brother's Circus, had a kinetic energy of 12, 000 J just prior to hitting the bucket of water. If Missy's mass is 40 kg, then how high was her platform? • Through the conservation of energy, KE = PE • Since she has 12000 J of KE at entry, she had 12000 J PE at the top of the platform • PE = mgh • 12000 J = (40 kg)(9. 8 m/s 2)h • h = 30. 6 m (and yes, it should be the same answer!!)

Putting It Together • An 80 kg student climbed onto a 5 m platform. How work did the student perform to get on the platform? • How much potential energy does the student have on top of the platform? • If the student jumps off the platform, what velocity will the student have when they land? • How long did it take the student to land?

Putting It Together • An 80 kg student climbed onto a 5. 0 m platform. How work did the student perform to get on the platform? – W = Fd = (ma)d – W = (80 kg)(9. 8 m/s 2)(5. 0 m) = 3920 J = 3. 92 k. J

Putting It Together • How much potential energy does the student have on top of the platform? – Remember, Work = PE = KE – Short Version – Since the Work was 3920 J, PE = 3920 J – Long Version • PE = mgh • PE = (80 kg)(9. 8 m/s 2)(5. 0 m) = 3920 J • Notice it’s the same number!!!

Putting It Together • If the student jumps off the platform, what velocity will the student have when they land? • • • Remember PE = KE If PE = 3920 J, then KE = 3920 J = ½ mv 2 3920 J = ½ (80 kg)v 2 V = 9. 98 m/s

Putting It Together – Review • How long the student was in the air after jumping off of the 5. 0 m platform? • One Way – d = (1/2)gt 2 – 5. 0 m = ½(9. 8 m/s 2)t 2 – t = 1. 01 s • The Other Way – – Their final velocity was 9. 98 m/s V = at 9. 98 m/s = (9. 8 m/s 2)(t) t = 1. 01 s (it’s the same – and should be!!)

Energy Conversion • A 0. 1 kg ball is taken to the top of a treehouse 20 m high. – What is the potential energy of this ball? – What is the kinetic energy and potential energy when it has fallen halfway? – How fast was the ball moving right before impact?

Energy Conversion • A 0. 1 kg ball is taken to the top of a treehouse 20 m high. – What is the potential energy of this ball? • PE = mgh • PE = (0. 1 kg)(9. 8 m/s 2)(20 m) • PE = 19. 6 J

Energy Conversion • A 0. 1 kg ball is taken to the top of a treehouse 20 m high. – What is the kinetic energy and potential energy when it has fallen halfway? – PE = mgh, halfway is 10 m – PE = (0. 1 kg)(9. 8 m/s 2)(10 m) = 9. 8 J – Note: Since the total energy of the system is 19. 6 J, the ball has 9. 8 J of PE and 9. 8 J of KE

Energy Conversions • A 0. 1 kg ball is taken to the top of a treehouse 20 m high. – How fast was the ball moving right before impact? • • At this point, all of the energy has been converted to KE KE = (1/2)mv 2 19. 6 J = (1/2)(0. 1 kg)v 2 v = 19. 8 m/s • Note – Since gravity accelerates an object at roughly 10 m/s/s, these numbers should make sense. If we plugged this into our old kinematics equations, the height and final speed would check out.

Power • Power is the rate of doing work (or the rate of energy transfer) – The faster work is performed, the more power a system has – Power is measured in watts (W) • Example: Your average light bulb is 40 or 60 KW

Power • One non-metric unit of power is horsepower (hp) – The power of a car engine is usually measured in horsepower – 1 hp = 0. 75 W

Example 1 • Our lifter that performed a 440 lb (200 kg) deadlift took 4. 0 s to complete his rep. The distance from the floor to lockout is 0. 6 m. How much power was generated?

Example 1 • Our lifter that performed a 440 lb (200 kg) deadlift took 4. 0 s to complete his rep. The distance from the floor to lockout is 0. 6 m. How much power was generated? • Power = Work/Time • Power = Fd/Dt = (ma)d/Dt • Power = (200 kg)(9. 8 m/s 2)(0. 6 m)/(4. 0 s) = 817 watts

Example 2 • Earlier that day, our same lifter performed a 220 lb (100 kg) power clean, which took 1. 0 s to complete his rep. The distance from the floor to lockout is 1. 25 m (it’s a longer range of motion!). How much power was generated?

Example 2 • Earlier that day, our same lifter performed a 220 lb (100 kg) power clearn, which took 1. 0 s to complete his rep. The distance from the floor to lockout is 1. 25 m (it’s a longer range of motion!). How much power was generated? • Power = Work/Time • Power = Fd/Dt = (ma)d/Dt • Power = (100 kg)(9. 8 m/s 2)(1. 25 m)/(1. 0 s) = 1225 watts or 1. 2 k. W – Notice, less time = more POWER!

Example 3 • Ryan hauls his piano up two flights of stairs (22 m) in 5 minutes. The piano’s mass is 90. 7 kg. What power is used?

Example 3 • Ryan hauls his piano up two flights of stairs (22 m) in 5 minutes. The piano’s mass is 90. 7 kg. What power is used? • Power = W/T = Fd/time = (ma)d/t • Power = (90. 7 kg)(9. 8 m/s 2)(22 m)/(300 s) = 65. 2 W

Example 4 • What if Ryan managed to move the same 90. 7 kg piano 22 m in only 20 s?

Example 4 • What if Ryan managed to move the same 90. 7 kg piano 22 m in only 20 s? • Power = W/T = Fd/time = (ma)d/t • Power = (90. 7 kg)(9. 8 m/s 2)(22 m)/(20 s) = 978 W – Less time, more POWER!!

Example 5 • An engine moves a boat through the water at a constant speed of 15 m/s. The engine must exert a force of 6. 0 x 103 N to balance the force that water exerts against the hull. What power does the engine develop?

Example 5 • An engine moves a boat through the water at a constant speed of 15 m/s. The engine must exert a force of 6. 0 x 103 N to balance the force that water exerts against the hull. What power does the engine develop? • Power = Fd/t • Remember, d/t = v, so Power = Fv • Power = (6. 0 x 103 N)(15 m/s) = 9. 0 x 104 W or 90 k. W