Wireless Propagation Signal Strength Measure signal strength in

Wireless Propagation

Signal Strength • Measure signal strength in – d. BW = 10*log(Power in Watts) – d. Bm = 10*log(Power in m. W) • 802. 11 can legally transmit at 30 d. Bm (1 W) (for 802. 11 a it is more complicated) • Most 802. 11 PCMCIA cards transmit at 10 -20 d. Bm (why? ) • Mica 2 (cross bow wireless node) can transmit from – 20 d. Bm to 5 d. Bm. (10 micro. W to 3 m. W) • Mobile phone base station: 20 W, but 60 users, so 0. 3 W / user, but antenna has gain=18 d. Bi. • Mobile phone handset: 21 d. Bm

Noise • Interference – From other transmitters – From other equipment • E. g. , microwave ovens 20 d. Bm 50% duty-cycle with 16 ms period. – Noise in the electronics – e. g. , digital circuit noise on analogue parts. – Non-linearities in circuits. – Often modeled as white Gaussian noise, but this is not always a valid assumption. • Thermal noise – Due to thermal agitation of electrons. Present in all electronics and transmission media. – k. T(W/hz) • k Boltzmann’s constant = 1. 38 10 -23 • T – temperture in Kelvin (C+273) – k. TB(W) • B bandwidth – E. g. , • Temp = 293, => -203 d. B, -173 d. Bm /Hz • Temp 293 and 22 MHz => -130 d. B, -100 d. Bm

Signal to Noise Ratio (SNR) • • SNR = signal power / noise power SNR (d. B) = 10*log 10(signal power / noise power) Signal strength is the transmitted power multiplied by a gain – impairments Impairments – – – The transmitter is far away. The signal passes through rain or fog and the frequency is high. The signal must pass through an object. The signal reflects of an object, but not all of the energy is reflected. The signal interferes with itself – multi-path fading An object not directly in the way impairs the transmission.

Receiver Sensitivity • The received signal must have a strength that is larger than the receiver sensitivity • 20 d. B larger would be good. (More on this later) • E. g. , – 802. 11 b – Cisco Aironet 250 (the most sensitive) • 1 Mbps: -94 d. Bm; 2 Mbps: -91 d. Bm; 5. 5 Mbps: -89 d. Bm; 11 Mbps: -85 d. Bm – Mobile phone base station: -119 d. Bm – Mobile phone hand set: -118 d. Bm – Mica 2 at 868/916 MHz: -98 d. Bm

Simple link budget • Determine if received signal is larger than the receiver sensitivity • Must account for effective transmission power – Transmission power – Antenna gain – Losses in cable and connectors. • Path losses – Attenuation – Ground reflection – Fading (self-interference) • Receiver – Receiver sensitivity – Losses in cable and connectors

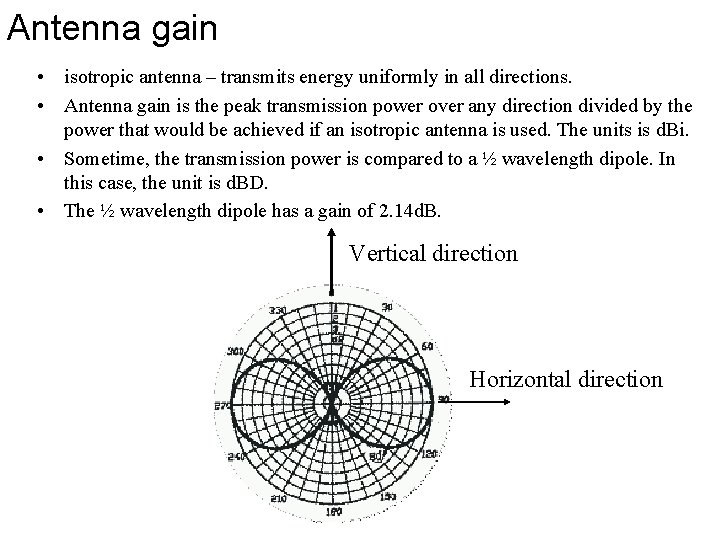
Antenna gain • isotropic antenna – transmits energy uniformly in all directions. • Antenna gain is the peak transmission power over any direction divided by the power that would be achieved if an isotropic antenna is used. The units is d. Bi. • Sometime, the transmission power is compared to a ½ wavelength dipole. In this case, the unit is d. BD. • The ½ wavelength dipole has a gain of 2. 14 d. B. Vertical direction Horizontal direction

Antenna gain • Antenna gain is increased by focusing the antenna – The antenna does not create energy, so a higher gain in one direction must mean a lower gain in another. – Note: antenna gain is based on the maximum gain, not the average over a region. This maximum may only be achieved only if the antenna is carefully aimed. This antenna is narrower and results in 3 d. B higher gain than the dipole, hence, 3 d. BD or 5. 14 d. Bi This antenna is narrower and results in 9 d. B higher gain than the dipole, hence, 9 d. BD or 11. 14 d. Bi

Antenna gain Instead of the energy going in all horizontal directions, a reflector can be placed so it only goes in one direction => another 3 d. B of gain, 3 d. BD or 5. 14 d. Bi Further focusing on a sector results in more gain. A uniform 3 sector antenna system would give 4. 77 d. B more. A 10 degree “range” 15 d. B more. Mobile phone base stations claim a gain of 18 d. Bi with three sector antenna system. • Cover 15 degree vertical (360/15 = 24 or 10 log 10(24)d. Bi = 13. 8 d. Bi from vertical) • 3 sector, 10 log 10(3) =4. 77 d. Bi • 13. 8+4. 77 – loss = 18 d. Bi

Simple link budget – 802. 11 g receiver sensitivity • 6 Mbps – – – Thermal noise: -174 d. Bm/Hz Channel noise (22 MHz): 73 d. B Noise factor: 10 d. B Noise power (sum of the above): -91 d. Bm Receiver requirements: • 3 d. B is the minimum SNR (see next slide) – Min receiver signal strength: -88 d. Bm • 54 Mbps – – – Thermal noise: -174 d. Bm/Hz Channel noise (22 MHz): 73 d. B Noise factor: 10 d. B Noise power (sum of the above): -91 d. Bm Receiver requirements: • 20 d. B is the minimum SNR (see next slide) – Min receiver signal strength: -71 d. Bm

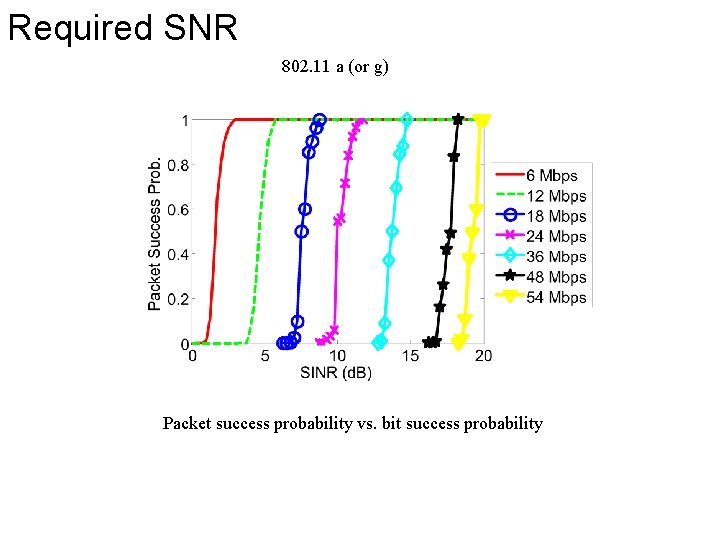
Required SNR 802. 11 a (or g) Packet success probability vs. bit success probability

Simple link budget – 802. 11 g example • From base station (6 Mbps) – – – • From PCMCIA to base station – – – • +20 d. Bm transmission power +6 d. Bi transmit antenna gain +2. 2 d. Bi receiver antenna gain -88 d. Bm minimum receiver power => 116. 2 d. B path losses => 113. 2 d. B path losses if 3 d. B of link margin is added (to ensure the link works well. ) +10 d. Bm transmission power +6 d. Bi transmit antenna gain +2. 2 d. Bi receiver antenna gain -88 d. Bm minimum receiver power => 106. 2 d. B path losses => 103. 2 d. B path losses if 3 d. B of link margin is added (to ensure the link works well. ) From base station (54 Mbps) – – – +20 d. Bm transmission power +6 d. Bi transmit antenna gain +2. 2 d. Bi receiver antenna gain -71 d. Bm minimum receiver power => 99. 2 d. B path losses => 96. 2 d. B path losses if 3 d. B of link margin is added (to ensure the link works well. )

Simple link budget – mobile phone – downlink example • • • • • Transmission power (base station): 20 W (can be as high as 100 W) Transmission power for voice (not control): 18 W Number of users: 60 Transmission power/user: 0. 3 W, 300 m. W, 24. 8 d. Bm Base station antenna gain (3 -sectors): 18 d. Bi Cable loss at base station: 2 d. B Effective isotropic radiated power: 40 d. Bm (sum of the above) Receiver: Thermal noise: -174 d. Bm/Hz Mobile station receiver noise figure (noise generated by the receiver, Johnson Noise, ADC quantization, clock jitter): 7 d. B Receiver noise density: -167 d. B/Hz (-174+7) Receiver noise: -101. 2 d. Bm (assuming 3. 84 MHz bandwidth for CDMA) Processing gain: 25 d. B (CDMA is spread, when unspread(demodulated) and filtered, some of the wide band noise is removed) Required signal strength: 7. 9 d. B Receiver sensitivity: -101. 2 – 25 + 7. 9 = -118. 3 Body loss (loss due to your big head): 3 d. B Maximum path loss: 40 – (-118. 3) – 3 = 155. 3

Simple link budget – mobile phone – uplink example • • • • Transmission power (mobile): 0. 1 W (21 d. Bm) Antenna gain: 0 d. Bi Body loss: 3 d. B Effective isotropic radiated power: 18 d. Bm (sum of the above) (maximum allowable by FCC is 33 d. Bm at 1900 MHz and 20 d. Bm at 1700/2100 MHz Receiver/base station Thermal noise: -174 d. Bm/Hz Mobile station receiver noise figure (noise generated by the receiver, Johnson Noise, ADC quantization, clock jitter): 5 d. B Receiver noise density: -169 d. B/Hz (-174+5) Receiver noise: -103. 2 d. Bm (assuming 3. 84 MHz bandwidth for CDMA) Processing gain: 25 d. B (CDMA is spread, when unspread(demodulated) and filtered, some of the wide band noise is removed) Margin for interference: 3 d. B (more interference on the uplink than on the downlink) Required signal strength: 6. 1 d. B Receiver sensitivity: -119. 0 Maximum path loss: 153. 3

Shannon Capacity • Given SNR it is possible to find theoretical maximum bit-rate: • Effective bits/sec = B log 2(1 + SNR), where B is bandwidth • E. g. , – – B = 22 MHz, SNR = 2. 5 d. B (where 802. 11 at 6 Mbps gives a low bit error) 22 106 log 2(1 + 10^(2. 5/10)) = 32 Mbps Of course, 802. 11 a/g can only do 6 Mbps when the SNR = 2. 5 d. B – Today, Shannon capacity is not possible, but we can get within a few d. B. • SNR ~ 2. 5 d. B – 3 d. B • 22 106 log 2(1 + 10^((2. 5 -3)/10)) = 20 Mbps

Propagation • Required receiver signal strength minus Transmitted signal strength is often approximately – – – • 99 d. B 802. 11 base station -> laptop 79. 2 d. B 802. 11 b laptop -> base station 75. 4 d. B laptop -> laptop 155. 3 Mobile phone downlink 153. 3 Mobile phone uplink. Where does all this energy go… – – Free space propagation – not valid but a good start Ground reflection • – – – Wall reflections/transmission Diffraction Large-scale path loss models • • • – – 2 -ray – only valid in open areas. Not valid if buildings are nearby. Log-distance Log-normal shadowing Okumura Hata Longley-Rice Indoor propagation Small-scale path loss • • Rayleigh fading Rician Fading

Free Space Propagation • The surface area of a sphere of radius d is 4 d 2, so that the power flow per unit area w(power flux in watts/meter 2) at distance d from a transmitter antenna with input accepted power p. T and antenna gain GT is • The received signal strength depends on the “size” or aperture of the receiving antenna. If the antenna has an effective area A, then the received signal strength is PR = PT GT (A/ (4 d 2)) • • Define the receiver antenna gain GR = 4 A/ 2. = c/f • 2. 4 GHz=> = 3 e 8 m/s/2. 4 e 9/s = 12. 5 cm • 933 MHz => =32 cm. Receiver signal strength: PR = PT GT GR ( /4 d)2 PR (d. Bm) = PT (d. Bm) + GT (d. Bi) + GR (d. Bi) + 10 log 10 (( /4 )2)-10 log 10(d 2) 2. 4 GHz => 10 log 10 (( /4 )2) = -40 d. B 933 MHz => 10 log 10 (( /4 )2) = -32 d. B • •

Free Space Propagation - examples • Mobile phone downlink – – – • Mobile phone uplink – • = 12. 5 cm PR (d. Bm) = (PT GT GRL) (d. Bm) - 40 d. B + 10 log 10 (1/d 2) Or PR – (PT +GR + L) - 40 d. B = 10 log 10(1/d 2) Or 155 – 40 = 10 log 10 (1/d 2) = Or (155 -40)/20 = log 10 (1/d) Or d = 10^ ((155 -40)/20) = 562 Km or Wilmington DE to Boston MA d = 10^ ((153 -40)/20) = 446 Km 802. 11 – – PR - PT = -113. 2 d. Bm 6 Mbps • • • – 54 Mbps needs – 85 d. Bm • • d = 10(113. 2 -40)/20 = 4500 m d = 10(113. 2 -40 - 3)/20 = 3235 m with 3 d. B gain margin d = 10(113. 2 -40 – 3 - 9)/20 = 1148 m with 3 d. B gain margin and neglecting antenna gains d = 10(99. 2 -40)/20 = 912 m d = 10(99. 2 -40 - 3)/20 = 646 m with 3 d. B gain margin d = 10(99. 2 -40 – 3 - 9)/20 = 230 m with 3 d. B gain margin and neglecting antenna gains Mica 2 Mote – – – -98 d. Bm sensitivity 0 d. Bm transmission power d = 10^((98 -30)/20) = 2511 m

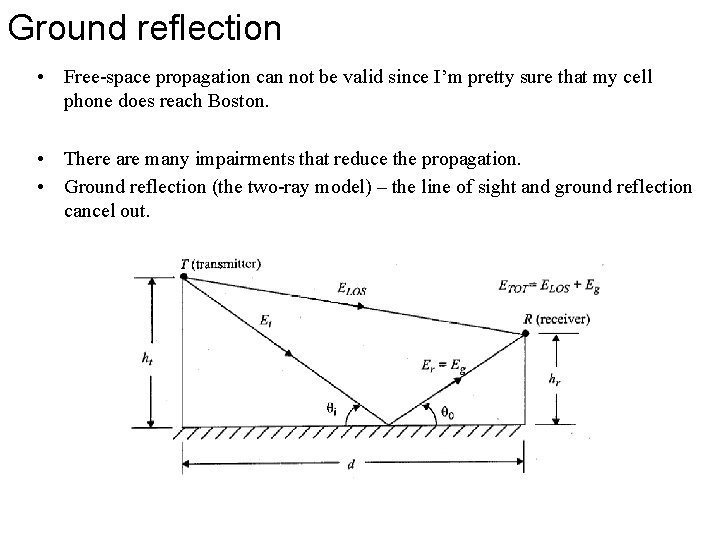
Ground reflection • Free-space propagation can not be valid since I’m pretty sure that my cell phone does reach Boston. • There are many impairments that reduce the propagation. • Ground reflection (the two-ray model) – the line of sight and ground reflection cancel out.

Ground reflection (approximate) • Approximation! When the wireless signal hits the ground, it is completely reflected but with a phase shift of pi (neither of these is exactly true). • The total signal is the sum of line of sight and the reflected signal. • The LOS signal is = Eo/d. LOS cos(2 / t) • The reflected signal is -1 Eo /d. GR cos(2 / (t – (d. GR-d. LOS))) • Phasors: – LOS = Eo/d. LOS 0 – Reflected = Eo/d. GR (d. GR-d. LOS) 2 / • For large d d. LOS = d. GR • Total energy – E = (Eo/d. LOS) ( (cos ((d. GR-d. LOS) 2 / ) – 1)2 + sin 2((d. GR-d. LOS) 2 / ) ) ½ – E = (Eo/d. LOS) 2 sin((d. GR-d. LOS) / )

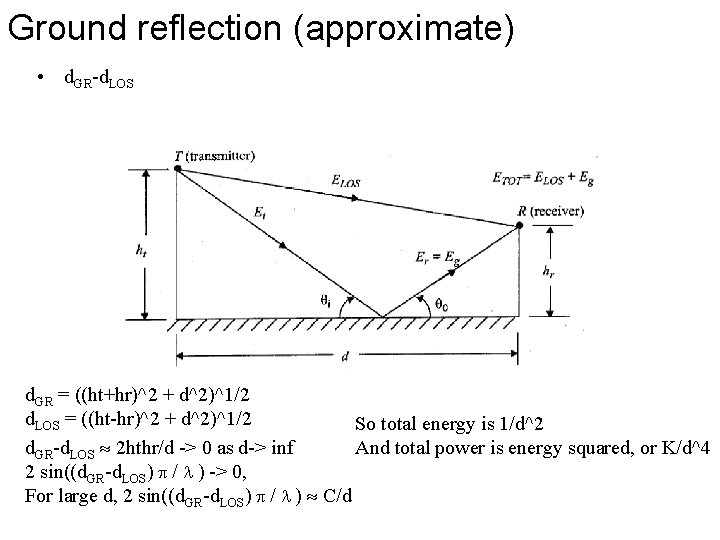
Ground reflection (approximate) • d. GR-d. LOS d. GR = ((ht+hr)^2 + d^2)^1/2 d. LOS = ((ht-hr)^2 + d^2)^1/2 So total energy is 1/d^2 And total power is energy squared, or K/d^4 d. GR-d. LOS 2 hthr/d -> 0 as d-> inf 2 sin((d. GR-d. LOS) / ) -> 0, For large d, 2 sin((d. GR-d. LOS) / ) C/d

Ground reflection (approximate) • • or • • Examples: Mobile phone – Suppose the base station is at 10 m and user at 1. 5 m – do = 1. 5 Km – d = 10^((155 – 40 + 20 log 10(do) )/40) = 29 Km • 802. 11 – Suppose the base station is at 1. 5 m and user at 1. 5 m – do = 226 m – 6 Mbps (20 d. B transmit power) • d = 10(113. 2 -40 + 20 log 10(do))/40 = 1016 m • d = 10(113. 2 -40 -3 – 8. 2 + 20 log 10(do))/40 = 533 m 3 d. B gain margin and neglecting antenna gains – 54 Mbps (20 d. B transmit power) • d = 10(99. 2 -40 + 20 log 10(do))/40 = 453 m • d = 10(99. 2 -40 -3 – 8. 2 + 20 log 10(do))/40 = 238 m 3 d. B gain margin and neglecting antenna gains • What is the impact of 3 d. B of power – Mobile phone: 34 Km – 802. 11: ~100 m (at 6 Mbps) and ~50 m (at 54 Mbps)

Ground reflection (more accurate) • When the signal reflects off of the ground, it is partially absorbed and the phase shift is not always . • Polarization • Transmission line model of reflections

Polarization The polarization could be such that the above picture is rotated by pi/2 along the axis. It could also be shifted. If a rotated and shifted

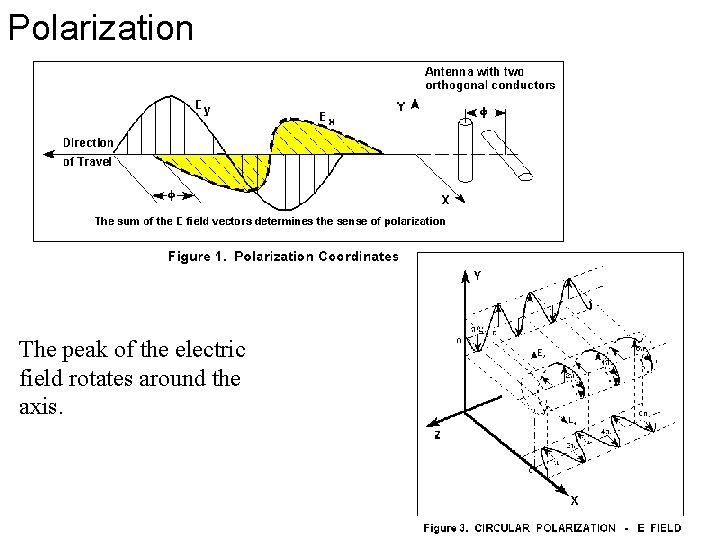
Polarization The peak of the electric field rotates around the axis.

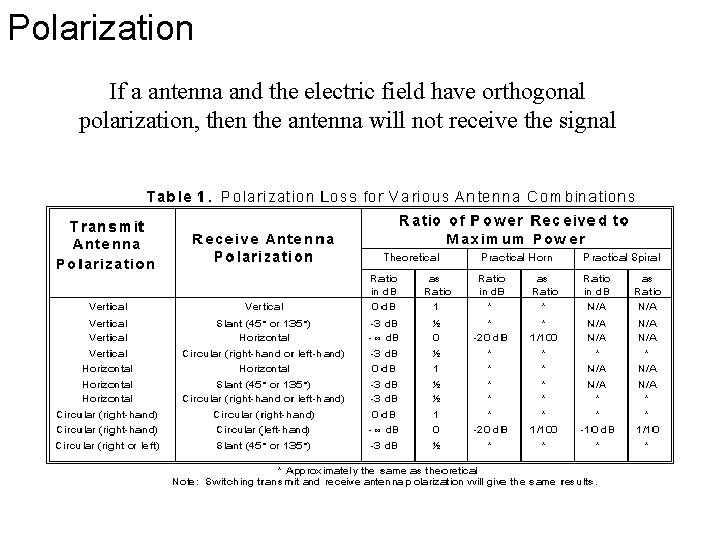
Polarization If a antenna and the electric field have orthogonal polarization, then the antenna will not receive the signal

Polarization • When a linearly polarized electric field reflects off of a vertical or horizontal wall, then the electric field maintains its polarization. • In practice, there are non-horizontal and non-vertical reflectors, and antenna are not exactly polarized. In practice, a vertically polarized signal can be received with a horizontally polarized antenna, but with a 20 d. B loss. • Theoretically, and sometimes in practice, it is possible to transmit two signals, one vertically polarized and one horizontally. Vertically/ horizontally polarized

Snell's Law for Oblique Incidence y x T T Graphical interpretation of Snell’s law

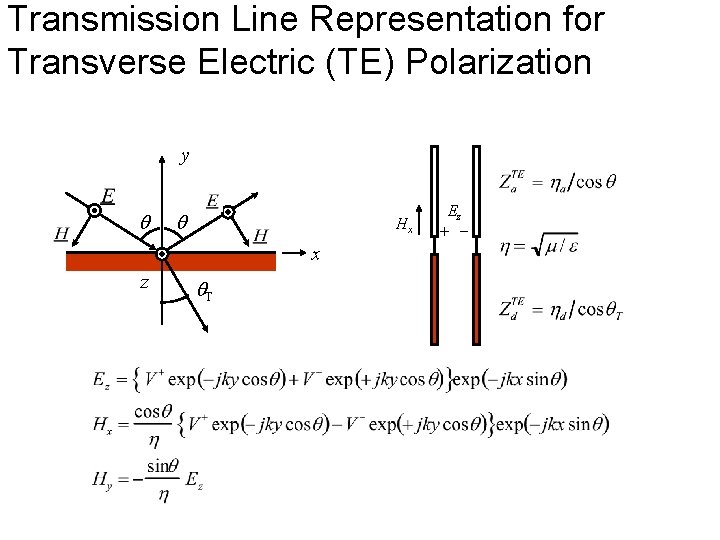
Transmission Line Representation for Transverse Electric (TE) Polarization y Hx x z T Ez + -

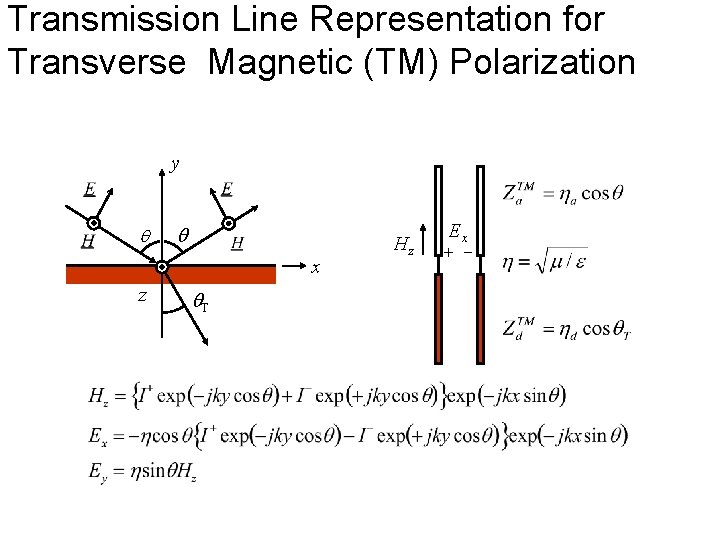
Transmission Line Representation for Transverse Magnetic (TM) Polarization y x z T Hz Ex + -

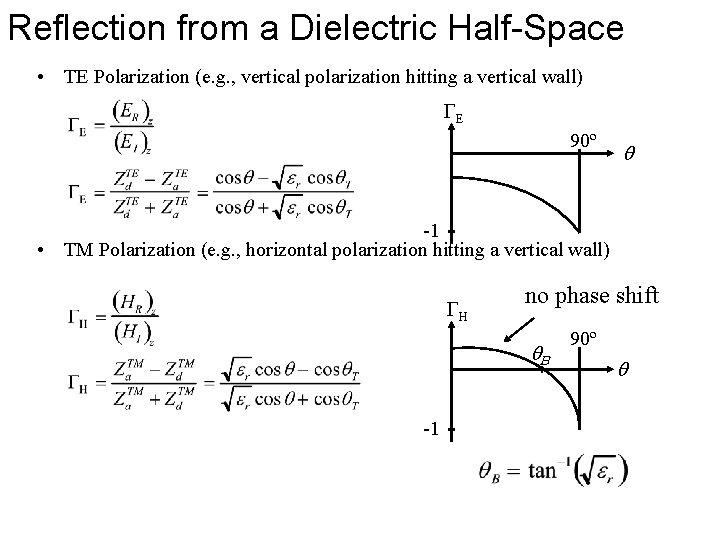
Reflection from a Dielectric Half-Space • TE Polarization (e. g. , vertical polarization hitting a vertical wall) GE 90º -1 • TM Polarization (e. g. , horizontal polarization hitting a vertical wall) GH no phase shift B -1 90º

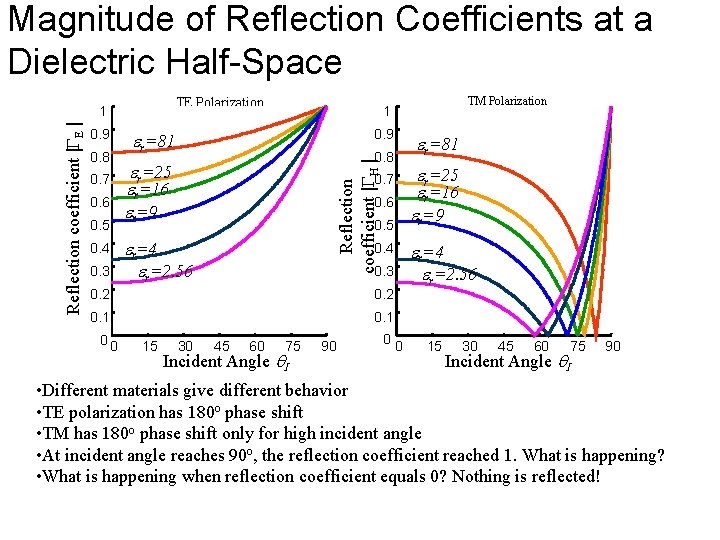
Magnitude of Reflection Coefficients at a Dielectric Half-Space TE Polarization 0. 9 0. 8 0. 7 0. 6 0. 5 0. 4 0. 3 0. 9 er=81 0. 8 er=25 er=16 er=9 0. 7 0. 6 0. 5 er=4 er=2. 56 0. 4 0. 3 0. 2 0. 1 00 15 30 45 60 TM Polarization 1 Reflection coefficient |GH | Reflection coefficient |GE | 1 75 Incident Angle I 90 00 er=81 er=25 er=16 er=9 er=4 er=2. 56 15 30 45 60 75 Incident Angle I 90 • Different materials give different behavior • TE polarization has 180 o phase shift • TM has 180 o phase shift only for high incident angle • At incident angle reaches 90 o, the reflection coefficient reached 1. What is happening? • What is happening when reflection coefficient equals 0? Nothing is reflected!

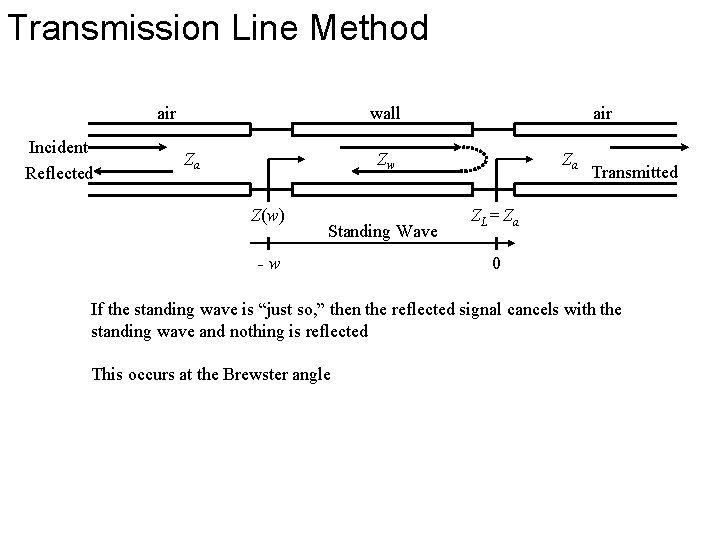
Transmission Line Method air Incident Reflected wall Za air Zw Z(w) Standing Wave -w Za Transmitted ZL = Za 0 If the standing wave is “just so, ” then the reflected signal cancels with the standing wave and nothing is reflected This occurs at the Brewster angle

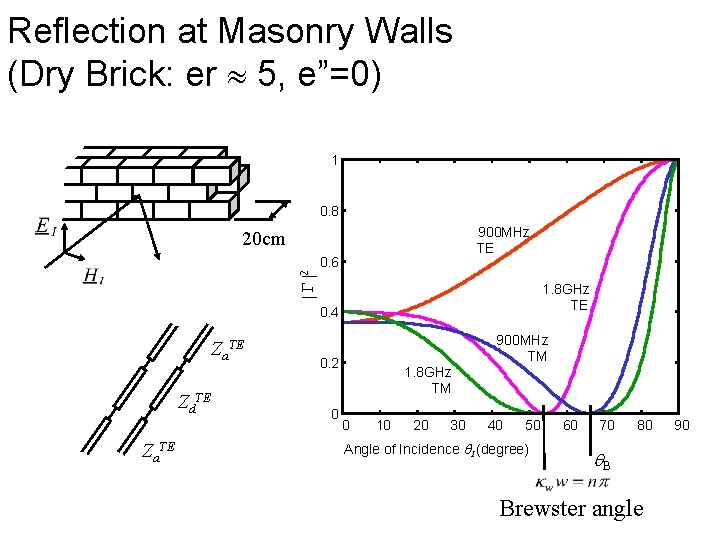
Reflection at Masonry Walls (Dry Brick: er 5, e”=0) 1 0. 8 900 MHz TE 20 cm G 2 0. 6 1. 8 GHz TE 0. 4 Za. TE Zd. TE Za. TE 900 MHz TM 0. 2 0 1. 8 GHz TM 0 10 20 30 40 50 Angle of Incidence I (degree) 60 70 80 B Brewster angle 90

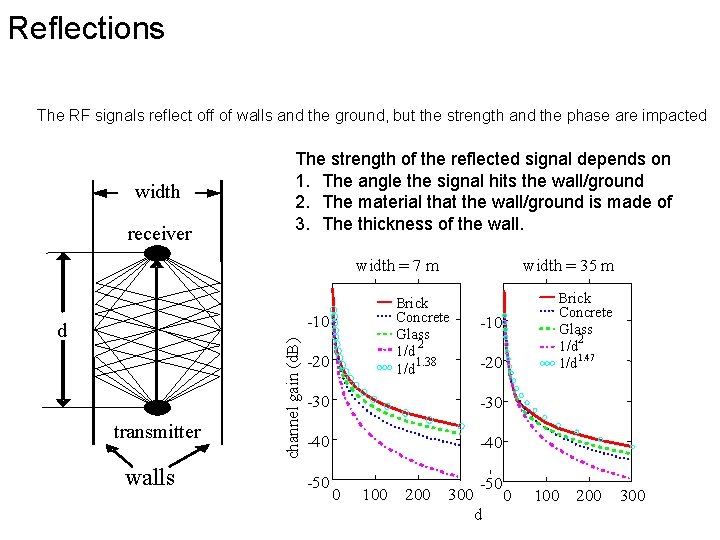
Reflections The RF signals reflect off of walls and the ground, but the strength and the phase are impacted width receiver The strength of the reflected signal depends on 1. The angle the signal hits the wall/ground 2. The material that the wall/ground is made of 3. The thickness of the wall. width = 7 m Brick Concrete Glass 2 1/d 1. 38 1/d transmitter walls channel gain (d. B) -10 d width = 35 m -20 -10 -20 -30 -40 -50 0 100 200 -50 300 0 d Brick Concrete Glass 2 1/d 1. 47 1/d 100 200 300

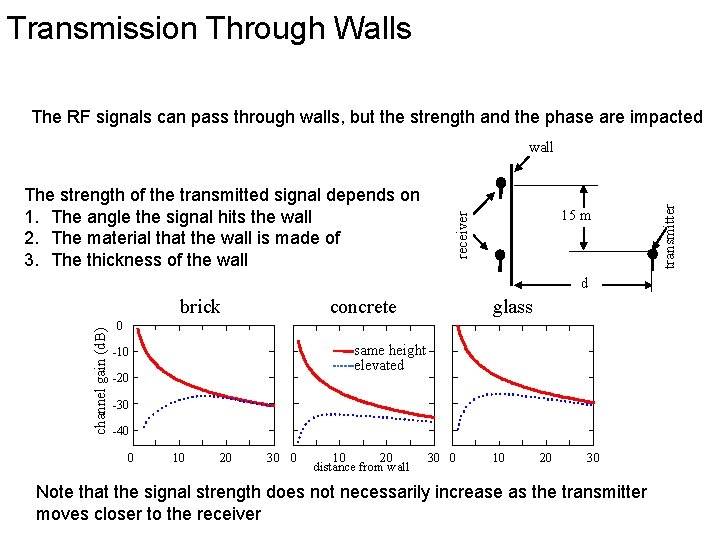
Transmission Through Walls The RF signals can pass through walls, but the strength and the phase are impacted 15 m receiver The strength of the transmitted signal depends on 1. The angle the signal hits the wall 2. The material that the wall is made of 3. The thickness of the wall d channel gain (d. B) brick concrete glass 0 same height elevated -10 -20 -30 -40 0 10 20 30 0 10 20 distance from wall 30 0 10 20 30 Note that the signal strength does not necessarily increase as the transmitter moves closer to the receiver transmitter wall

Ground reflection • See Mathcad file

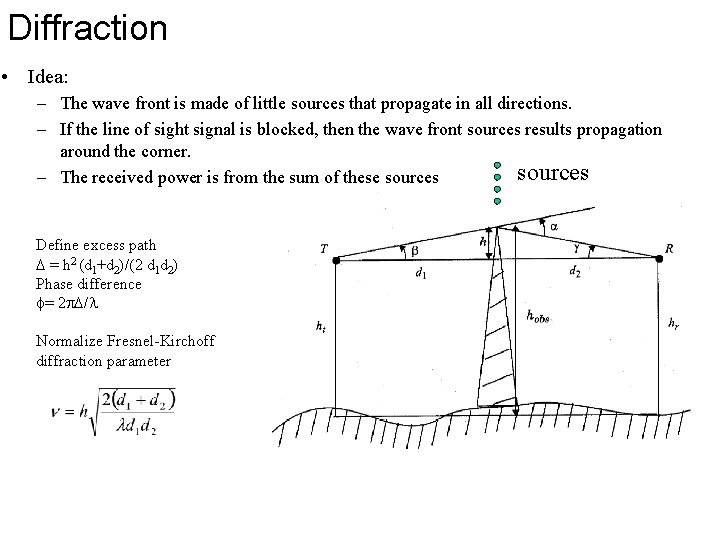
Diffraction • Idea: – The wave front is made of little sources that propagate in all directions. – If the line of sight signal is blocked, then the wave front sources results propagation around the corner. sources – The received power is from the sum of these sources Define excess path = h 2 (d 1+d 2)/(2 d 1 d 2) Phase difference f= 2 / Normalize Fresnel-Kirchoff diffraction parameter

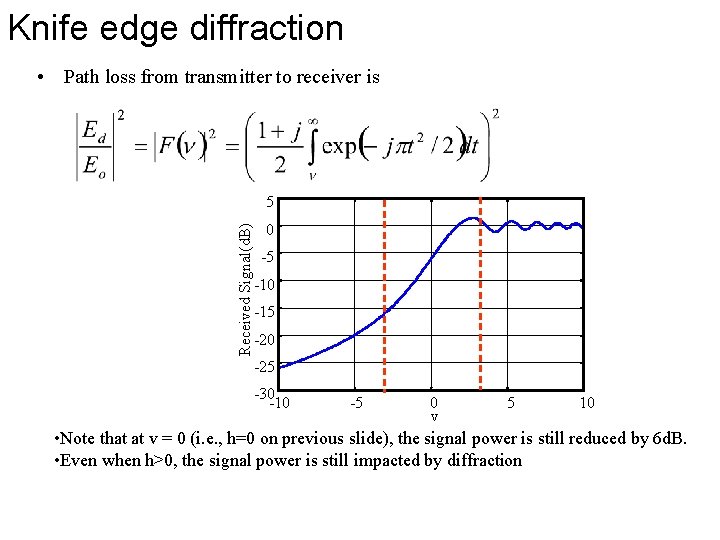
Knife edge diffraction • Path loss from transmitter to receiver is Received Signal(d. B) 5 0 -5 -10 -15 -20 -25 -30 -10 -5 0 v 5 10 • Note that at v = 0 (i. e. , h=0 on previous slide), the signal power is still reduced by 6 d. B. • Even when h>0, the signal power is still impacted by diffraction

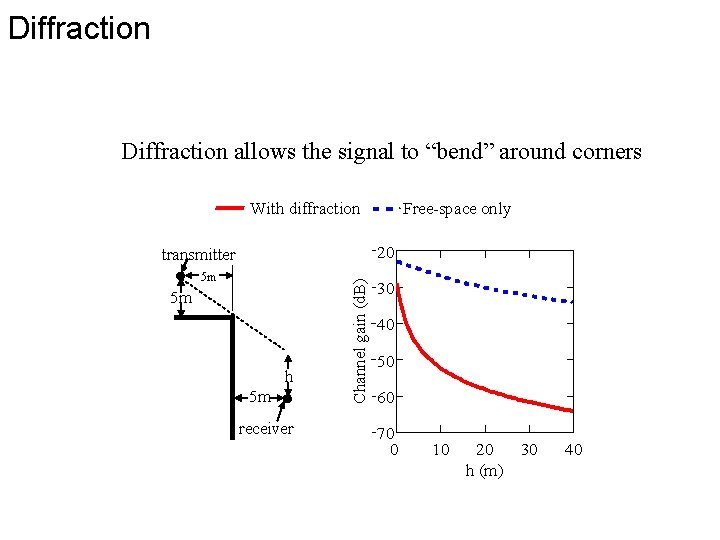
Diffraction allows the signal to “bend” around corners With diffraction Free-space only 20 5 m 5 m h 5 m receiver Channel gain (d. B) transmitter 30 40 50 60 70 0 10 20 h (m) 30 40

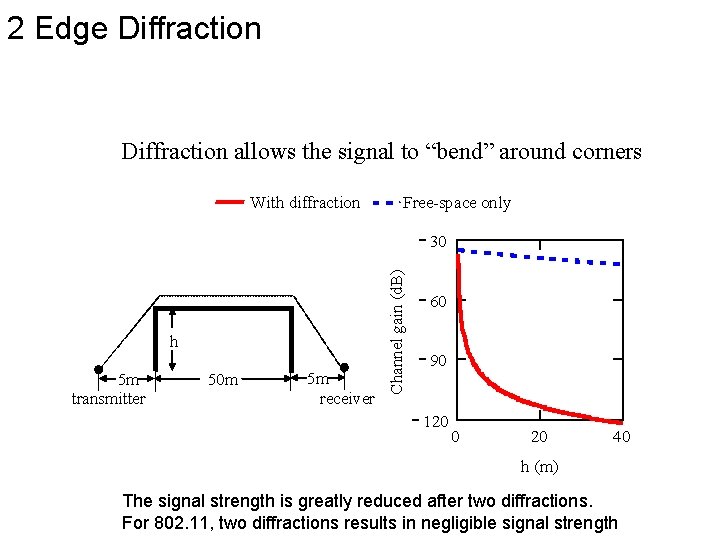
2 Edge Diffraction allows the signal to “bend” around corners With diffraction Free-space only h 5 m transmitter 50 m 5 m receiver Channel gain (d. B) 30 60 90 120 0 20 40 h (m) The signal strength is greatly reduced after two diffractions. For 802. 11, two diffractions results in negligible signal strength

Multiple diffractions • If there are two diffractions, there are some models. For more than 2 edges, the models are not very good. • On the other hand, there is so much loss after more than 2 edges, that the models are not very useful. For example, the signal might be stronger from just passing through the object than diffracting around it.

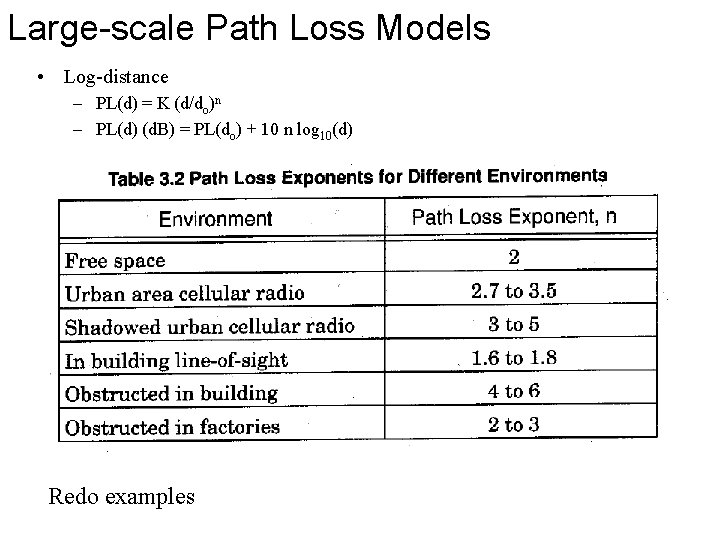
Large-scale Path Loss Models • Log-distance – PL(d) = K (d/do)n – PL(d) (d. B) = PL(do) + 10 n log 10(d) Redo examples

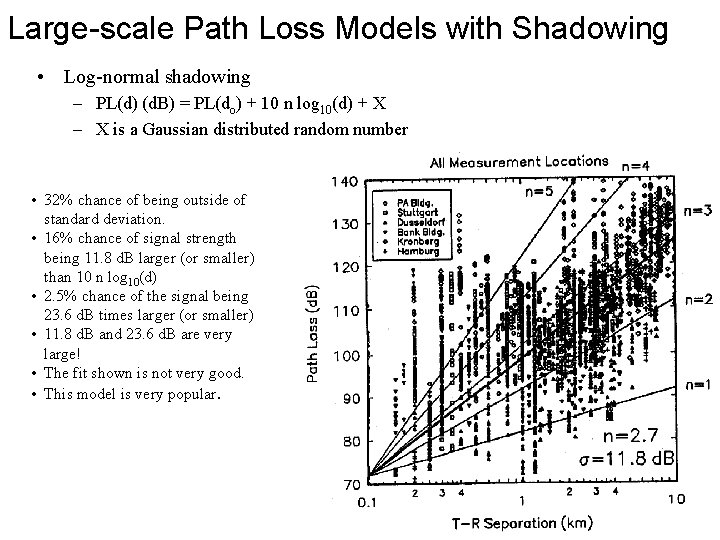
Large-scale Path Loss Models with Shadowing • Log-normal shadowing – PL(d) (d. B) = PL(do) + 10 n log 10(d) + X – X is a Gaussian distributed random number • 32% chance of being outside of standard deviation. • 16% chance of signal strength being 11. 8 d. B larger (or smaller) than 10 n log 10(d) • 2. 5% chance of the signal being 23. 6 d. B times larger (or smaller) • 11. 8 d. B and 23. 6 d. B are very large! • The fit shown is not very good. • This model is very popular.

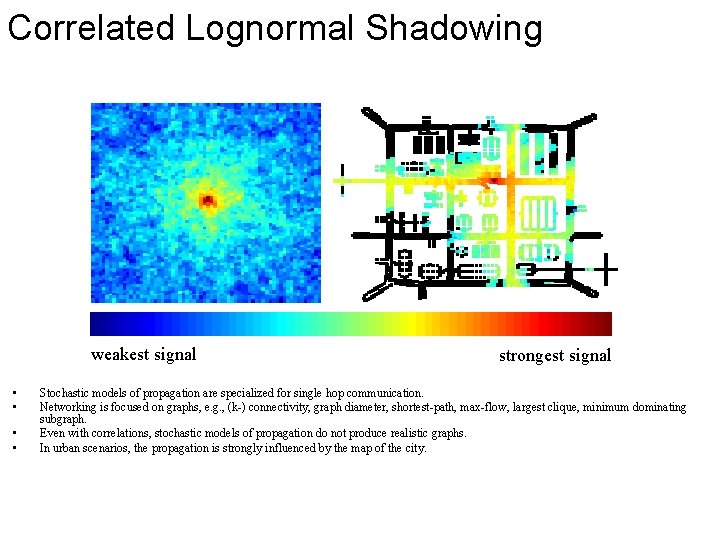
Correlated Lognormal Shadowing weakest signal • • strongest signal Stochastic models of propagation are specialized for single hop communication. Networking is focused on graphs, e. g. , (k-) connectivity, graph diameter, shortest-path, max-flow, largest clique, minimum dominating subgraph. Even with correlations, stochastic models of propagation do not produce realistic graphs. In urban scenarios, the propagation is strongly influenced by the map of the city.

Outdoor propagation models • Okumura – – – Empirical model Several adjustments to free-space propagation Path Loss L(d) = Lfree space + Amu(f, d) – G(ht) – G(hr) – GArea A is the median attenuation relative to free-space G(ht) = 20 log(ht /200) is the base station height gain factor G(hr) is the receiver height gain factor • G(hr) = 10 log(hr /3) for hr <3 • G(hr) = 20 log(hr /3) for hr >3 – Garea is the environmental correction factor

Hata Model • Valid from 150 MHz to 1500 MHz • A standard formula • For urban areas the formula is: – L 50(urban, d)(d. B) = 69. 55 + 26. 16 logfc - 13. 82 loghte – a(hre) + (44. 9 – 6. 55 loghte)logd where fc is the ferquency in MHz hte is effective transmitter antenna height in meters (30 -200 m) hre is effective receiver antenna height in meters (1 -10 m) d is T-R separation in km a(hre) is the correction factor for effective mobile antenna height which is a function of coverage area a(hre) = (1. 1 logfc – 0. 7)hre – (1. 56 logfc – 0. 8) d. B for a small to medium sized city

Indoor propagation models • Types of propagation – Line of sight – Through obstructions • Approaches – Log-normal – Site specific – attenuation factor model • Log-normal – PL(d)[d. Bm] = PL(d 0) + 10 nlog(d/d 0) + Xs • n and s depend on the type of the building • Smaller value for s indicates the accuracy of the path loss model.

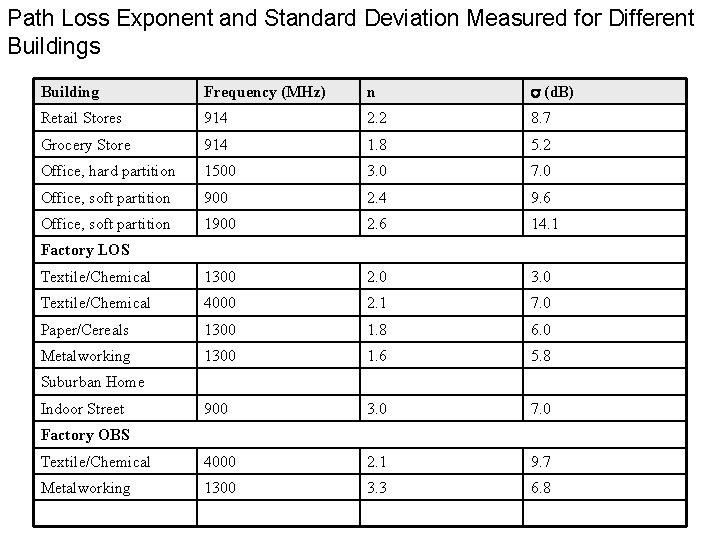
Path Loss Exponent and Standard Deviation Measured for Different Buildings Building Frequency (MHz) n s (d. B) Retail Stores 914 2. 2 8. 7 Grocery Store 914 1. 8 5. 2 Office, hard partition 1500 3. 0 7. 0 Office, soft partition 900 2. 4 9. 6 Office, soft partition 1900 2. 6 14. 1 Textile/Chemical 1300 2. 0 3. 0 Textile/Chemical 4000 2. 1 7. 0 Paper/Cereals 1300 1. 8 6. 0 Metalworking 1300 1. 6 5. 8 900 3. 0 7. 0 Textile/Chemical 4000 2. 1 9. 7 Metalworking 1300 3. 3 6. 8 Factory LOS Suburban Home Indoor Street Factory OBS

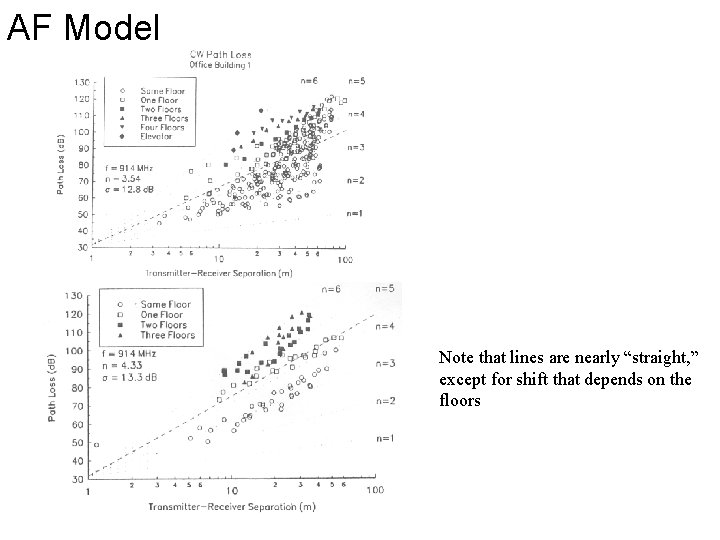
Site specific – attenuation factor (AF) model • PL(d) (d. B) = PL(do) + 10 n log(d/do) + FAF + PAF • FAF floor attenuation factor - Losses between floors – • Note that the increase in attenuation decreases as the number of floors increases. PAF partition attenuation factor - Losses due to passing through different types of materials – Use straight line between transmitter and receiver and count objects the line passes through FAF (d. B) s (d. B) Through 1 Floor 12. 9 7. 0 Through 2 Floors 18. 7 2. 8 Through 3 Floors 24. 4 1. 7 Through 4 Floors 27. 0 1. 5 Through 1 Floor 16. 2 2. 9 Through 2 Floors 27. 5 5. 4 Through 3 Floors 31. 6 7. 2 Building Office Building 1 Office Building 2

AF Model Note that lines are nearly “straight, ” except for shift that depends on the floors

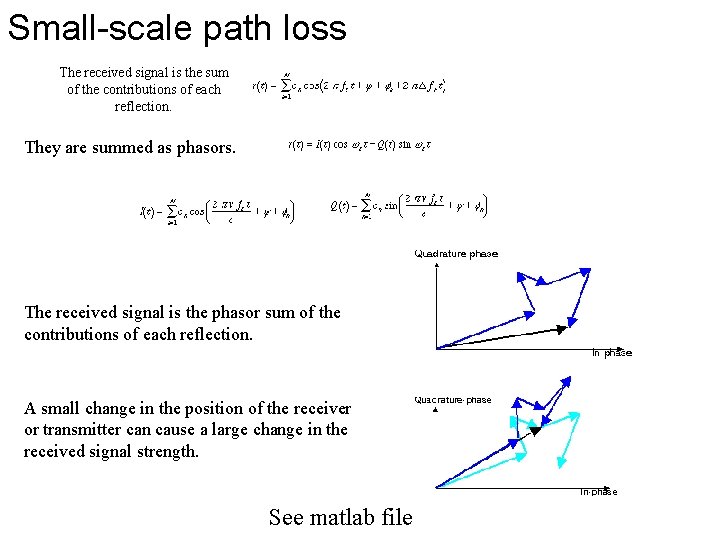
Small-scale path loss The received signal is the sum of the contributions of each reflection. They are summed as phasors. The received signal is the phasor sum of the contributions of each reflection. A small change in the position of the receiver or transmitter can cause a large change in the received signal strength. See matlab file

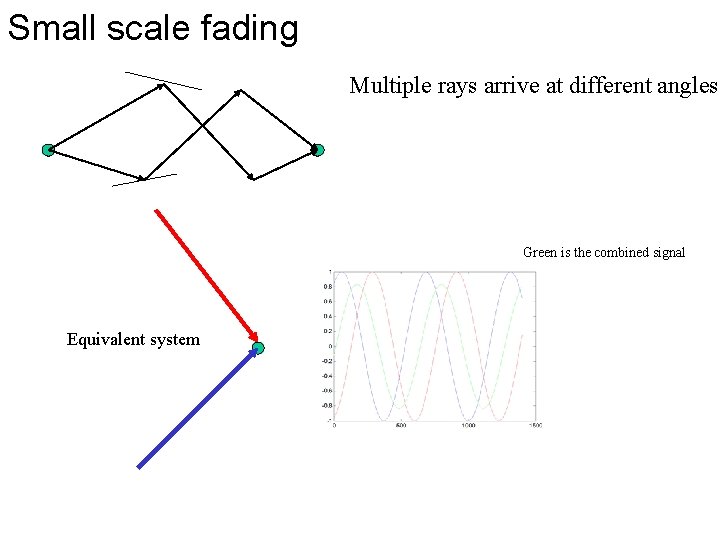
Small scale fading Multiple rays arrive at different angles Green is the combined signal Equivalent system

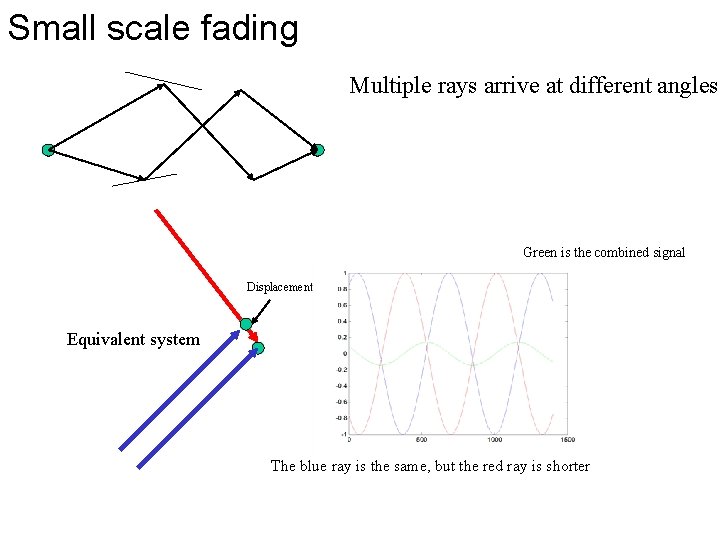
Small scale fading Multiple rays arrive at different angles Green is the combined signal Displacement of sensor/antenna Equivalent system The blue ray is the same, but the red ray is shorter

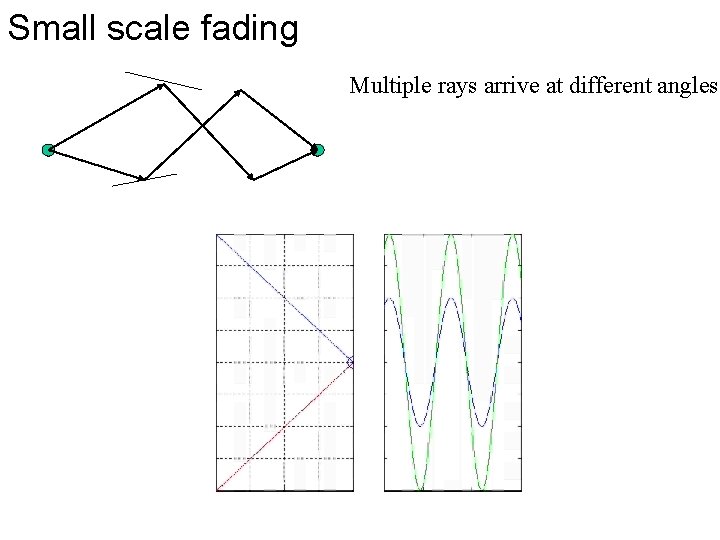
Small scale fading Multiple rays arrive at different angles

Rayleigh and Rician Fading • The inphase and quadrature parts can be modeled as independent Gaussian random variables. • The energy is the (X 2 + Y 2)1/2 where X and Y are Gaussian => the energy is Rayleigh distributed. • The power is (X 2 + Y 2) which is exponentially distributed. • Rician – if there is a strong line-of-sight component as well as reflections. Then the signal strength has a Ricain distribution.

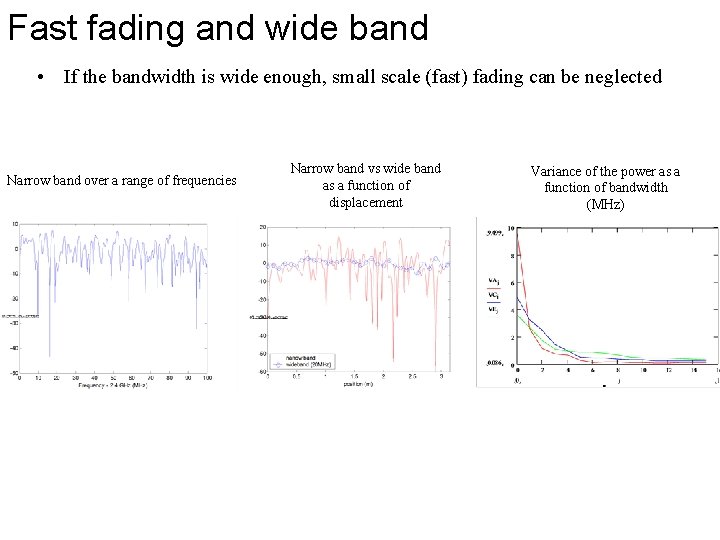
Fast fading and wide band • If the bandwidth is wide enough, small scale (fast) fading can be neglected Narrow band over a range of frequencies Narrow band vs wide band as a function of displacement Variance of the power as a function of bandwidth (MHz)

Rayleigh fading The signal is random with Rayleigh distribution The signal power is exponentially distributed Combined Rayleigh and lognormal PL(d) (d. B) = PL(do) + 10 n log 10(d) + X + 10 log 10(Y) –X is a Gaussian distributed random number with mean 0 and standard deviation between 4 and 12 d. B –X is correlated over moderate distances (like under a few meters or a few tens of meters) –Y is exponential with mean 1/W where the channel gain is averaged over W “independent” Rayleigh channels

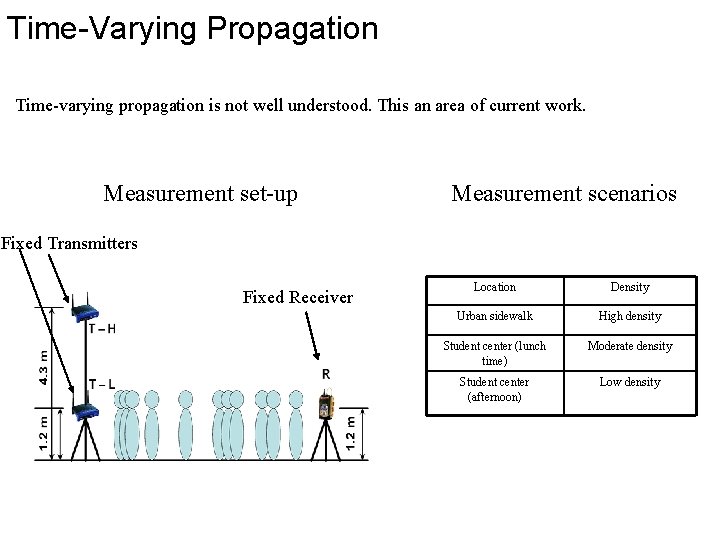
Time-Varying Propagation Time-varying propagation is not well understood. This an area of current work. Measurement set-up Measurement scenarios Fixed Transmitters Fixed Receiver Location Density Urban sidewalk High density Student center (lunch time) Moderate density Student center (afternoon) Low density

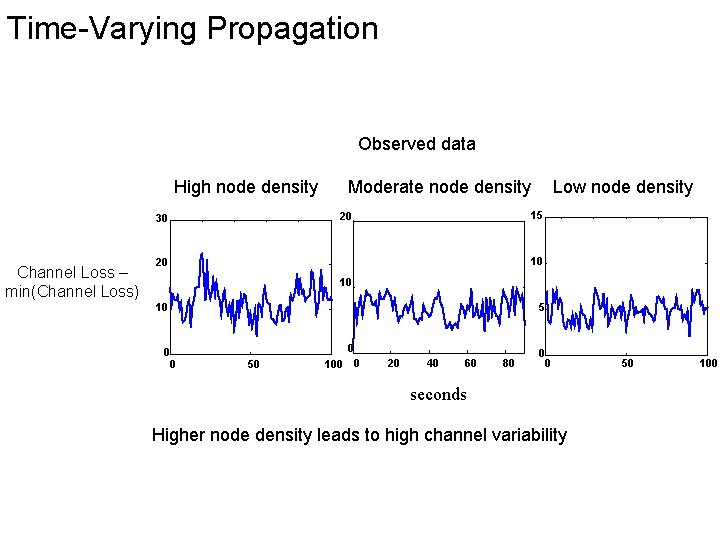
Time-Varying Propagation Observed data High node density Low node density 15 20 30 Channel Loss – min(Channel Loss) Moderate node density 10 20 10 10 5 0 0 0 50 100 0 20 40 60 80 0 0 seconds Higher node density leads to high channel variability 50 100

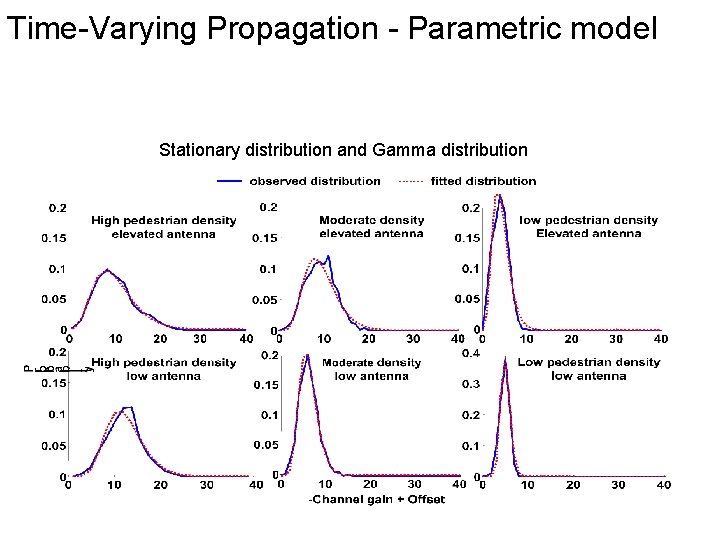
Time-Varying Propagation - Parametric model Stationary distribution and Gamma distribution

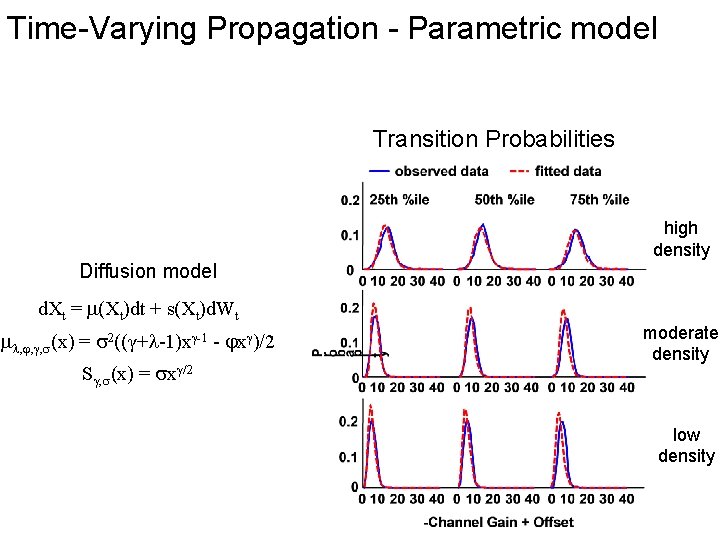
Time-Varying Propagation - Parametric model Transition Probabilities Diffusion model d. Xt = (Xt)dt + s(Xt)d. Wt , , , (x) = 2((γ+ -1)x -1 - x )/2 Sγ, (x) = xγ/2 high density moderate density low density

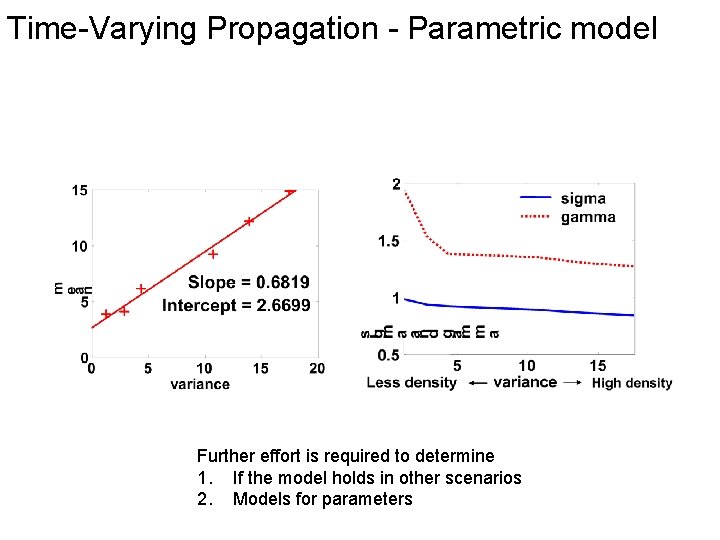
Time-Varying Propagation - Parametric model Further effort is required to determine 1. If the model holds in other scenarios 2. Models for parameters

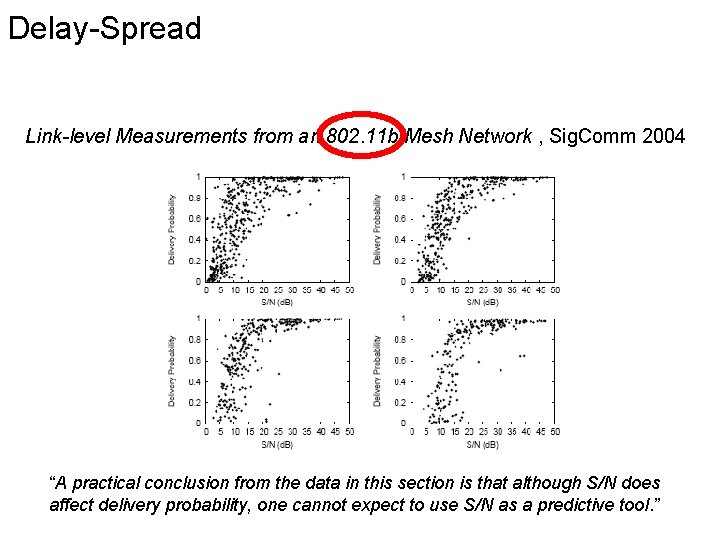
Delay-Spread Link-level Measurements from an 802. 11 b Mesh Network , Sig. Comm 2004 “A practical conclusion from the data in this section is that although S/N does affect delivery probability, one cannot expect to use S/N as a predictive tool. ”

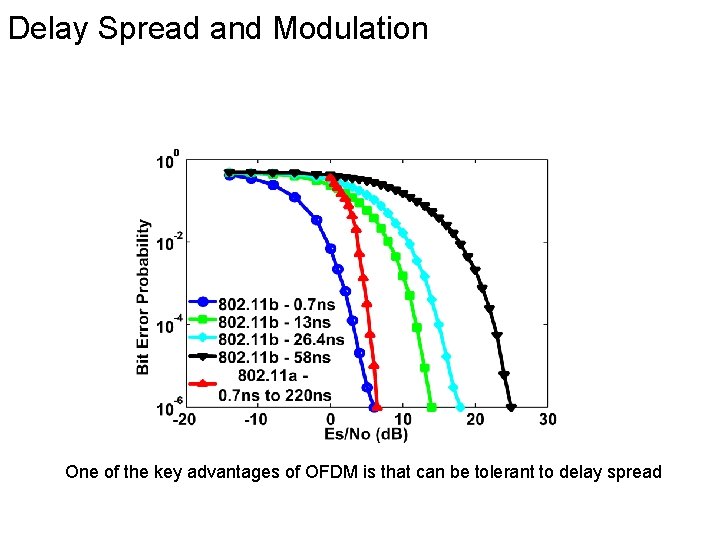
Delay Spread and Modulation One of the key advantages of OFDM is that can be tolerant to delay spread

Summary • The signal strength depends on the environment in a complicate way. • If objects are possible obstructing, then the signal strength may be log-normal distributed => large deviation from free-space • If the signal is narrow band, then the signal could be completely canceled out due to reflections and multiple paths. • Reflection, transmission, and diffraction can all be important

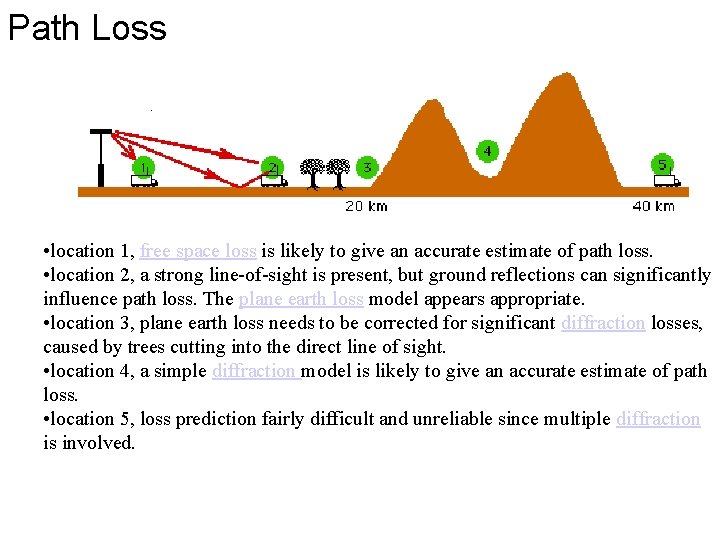
Path Loss • location 1, free space loss is likely to give an accurate estimate of path loss. • location 2, a strong line-of-sight is present, but ground reflections can significantly influence path loss. The plane earth loss model appears appropriate. • location 3, plane earth loss needs to be corrected for significant diffraction losses, caused by trees cutting into the direct line of sight. • location 4, a simple diffraction model is likely to give an accurate estimate of path loss. • location 5, loss prediction fairly difficult and unreliable since multiple diffraction is involved.