Wireless Information Transmission System Lab Introduction to Channel

Wireless Information Transmission System Lab. Introduction to Channel Estimation in OFDM Systems 2018/08/06 Wei-Wen Hu Institute of Communications National Sun Yat-sen

Outline Introduction System Model Channel Estimation Techniques in OFDM Systems LS Channel Estimation Linear Interpolation Channel Estimation MLS Channel Estimation LMMSE Channel Estimation 2

Wireless Information Transmission System Lab. Introduction Institute of Communications National Sun Yat-sen

Introduction In general, channel estimation can be cataloged into three kinds of estimation schemes: 1. Blind 2. Superimposed 3. Pilot-based The first two structures can obtain some bandwidth merit, but the computational complexity is usually not acceptable in practical realization. 4

Introduction The pilot-based estimation can be cataloged into two kinds of approaches: 1. The parameters are deterministic but unknown constant, such as maximum likelihood (ML) estimator and least square (LS) estimator. 2. The parameters are random variables, such as minimum mean square error (MMSE) estimator and maximum a posteriori (MAP) estimator. 5

Wireless Information Transmission System Lab. System Model Institute of Communications National Sun Yat-sen

The Transmitted OFDM Signal After the inverse discrete Fourier transform (IDFT) operation, the ith transmitted OFDM symbol in time domain can be expressed by: where and are an vector and an for modulated symbols and an IDFT matrix. 7 matrix standing

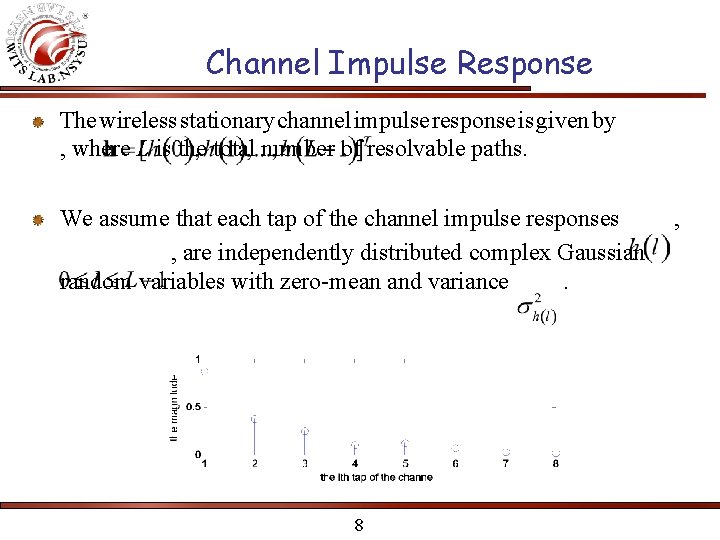
Channel Impulse Response The wireless stationary channel impulse response is given by , where L is the total number of resolvable paths. We assume that each tap of the channel impulse responses , are independently distributed complex Gaussian random variables with zero-mean and variance. 8 ,

Received Signal 9

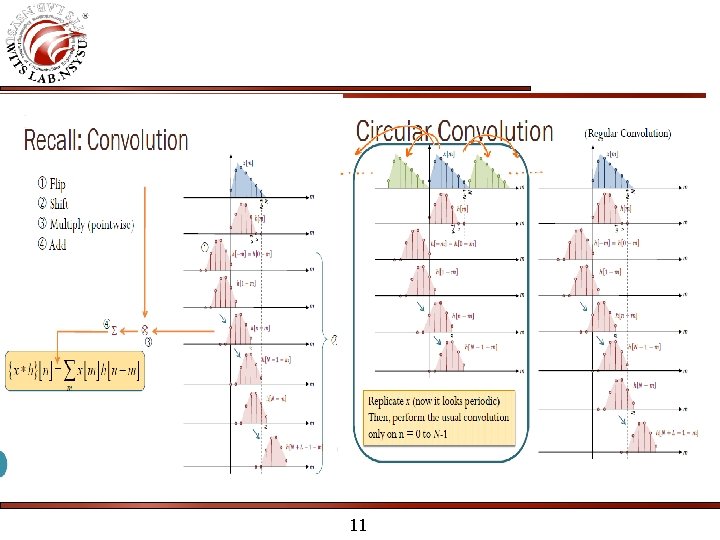
The Received CP-OFDM Symbol Assuming the synchronization is perfect and CP is adopted, the received ith OFDM symbol can be expressed as: where denotes the circular convolution and denotes the additive white Gaussian noise (AWGN) vector in the time domain with zero mean and variance. We note that there is no ICI and ISI in each OFDM symbol. 10

11

The Matrix Form of Channel is a circular convolution matrix, which can be given by 12

The Matrix Form of Channel The matrix G is constructed as follows: EX: Data = [1 2 3 4] Channel = [1 1] 13

The Matrix Form of Channel The matrix is constructed as follows: CP 14

The Received CP-OFDM Symbol If system is perfectly synchronized, and the CP is added and removed appropriately, there is no ISI and inter-carrier interference (ICI). After DFT operation, the ith received OFDM symbol in the frequency domain can be expressed as: where H is a N × N diagonal matrix denoting the channel response in frequency domain and is the AWGN in the frequency domain with covariance matrix. 15

The Received CP-OFDM Symbol Any circular matrix can be diagonalized by DFT matrix: 16

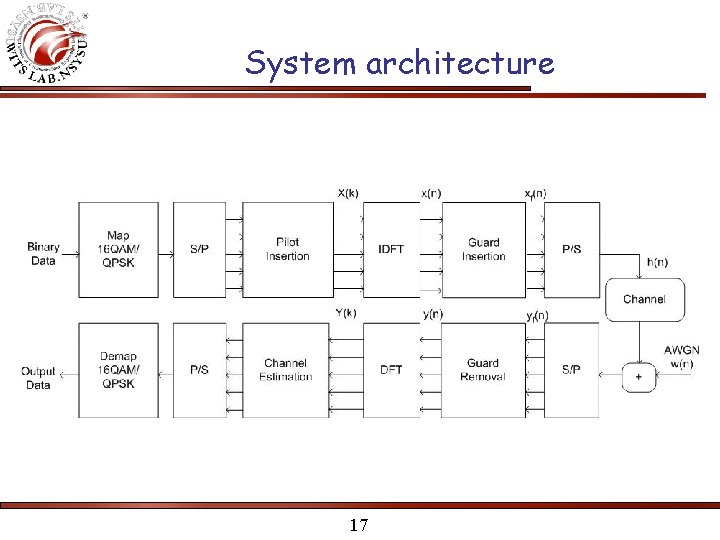
System architecture 17

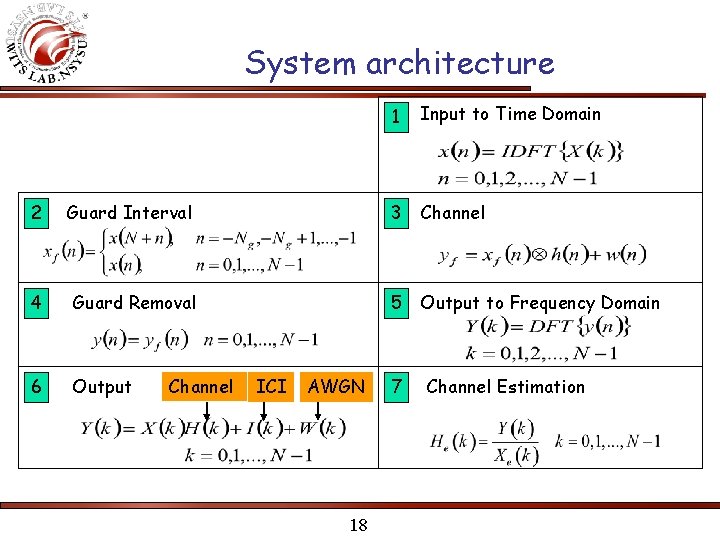
System architecture 1 Input to Time Domain 2 Guard Interval 3 Channel 4 Guard Removal 5 Output to Frequency Domain 6 Output Channel ICI AWGN 18 7 Channel Estimation

System Model Generally, the pilot symbols are multiplexed into an OFDM symbol in frequency domain: In addition, the power allocation of data and pilot symbols are given by: ρ: Total Power β: Power Allocation Factor N: Number of Subcarriers 19

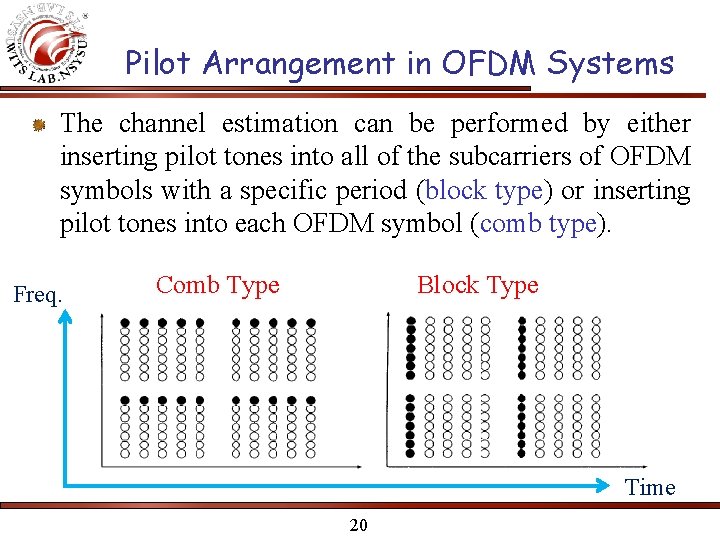
Pilot Arrangement in OFDM Systems The channel estimation can be performed by either inserting pilot tones into all of the subcarriers of OFDM symbols with a specific period (block type) or inserting pilot tones into each OFDM symbol (comb type). Freq. Comb Type Block Type Time 20

Wireless Information Transmission System Lab. Channel Estimation Techniques in OFDM Systems Institute of Communications National Sun Yat-sen

Least Square estimation In the simple case, the channel estimates, are found by straightforward multiplying the received pilot by the inverse of the known transmitted pilot. This method is called least square (LS) estimator as given by 22

The LMMSE Channel Estimator The linear minimum mean square error (LMMSE) estimator is given by [3, 4] where represents the cross-correlation between all the subcarriers and the pilot subcarriers, represents the autocorrelation matrix between the pilot subcarriers, and. The LMMSE estimator shown in (*) is for block-type pilot arrangement. Readers who are interested in LMMSE estimator for comb-type arrangement may refer to [5]. 23

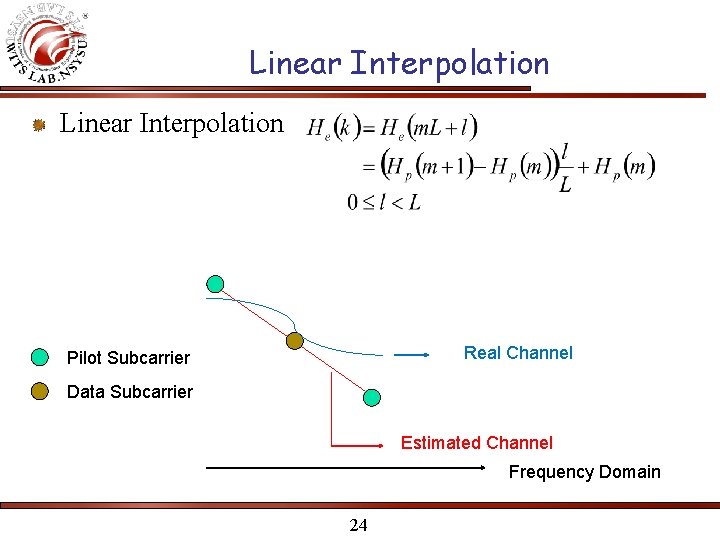
Linear Interpolation Real Channel Pilot Subcarrier Data Subcarrier Estimated Channel Frequency Domain 24

References [1] Sinem Coleri, Mustafa Ergen, Anuj Puri, and Ahmad Bahai, “Channel Estimation Techniques Based on Pilot Arrangement in OFDM Systems, ” IEEE transactions on Broadcasting, Vol. 48, No. 3, September 2002. [2] G. -S. Liu and C. -H. Wei, “A new variable fractional sample delay filter with nonlinear interpolation, ” IEEE Trans. Circuits and Systems-11: Anulog and. Digiral Signal Processing, vol. 39, no. 2, Feb. 1992. [3] O. Edfors, M. Sandell, J. -J. van de Beek, S. K. Wilson, and P. O. Borjesson, “OFDM Channel Estimation by Singular Value Decomposition, ” IEEE Transactions on Communications, vol. 46, no. 7, pp. 931 -939, Jul. 1998. [4] S. M. Kay, Fundamentals of Statistical Signal Processing: Estimation Theory, New Jersey: Prentice Hall, 1993, pp. 380 -382. [5] M. K. Ozdemir and H. Arslan, “Channel estimation for wireless OFDM systems, ” IEEE Communication Surveys & Tutorials, vol. 9, no. 2, pp. 18 -48, 2 nd Quarter, 2007 25

Appendix A. LMMSE estimator 26

Appendix A. LMMSE estimator 27

HW Consider an OFDM system with the number of subcarrier N = 128, and the length of CP NCP =16. The multi-path channel is given by where L = 6 is the number of resolvable paths. The channel taps , , are assumed to be independent complex Gaussian distributed random variables with zero mean and a variance , where , and is the normalization coefficient such that. 28

HW Pilot : ZC sequence (loaded on the subcarrier set [1: D: N]) First order interpolation is adopted. Exercise: Plot the MSE of channel estimation versus SNR in the cases of D=4 and D=8. 29