Wind Turbine Structure Design Ken Youssefi Engineering 10

Wind Turbine Structure Design Ken Youssefi Engineering 10, SJSU 1

Blade design • Do your research on rotor design: blade profile, blade number and angle of attack before going to the lab. • Finish modeling your blade during the lab next week • Make sure your blade is not too thin (less than 1. 5 mm or 1/16 inch), round the sharp edges and emboss the hub with your section and group number, S 10 G 9. • Your lab instructor will collect the. stl and part files at the end of the lab period. Ken Youssefi Engineering 10, SJSU 2

Blade edges too thin, not rounded Blade with rounded edge Emboss Group Blade with and section # on sharp edge the hub Do not cover the hole in the hub First blade modeled with rounded edge, rounded edges did not copied when array command created the other two. Ken Youssefi Engineering 10, SJSU 3

Wind Turbine Structure The Goal (Design objective) The support structure should be optimized for weight and stiffness (deflection) Minimize weight, maximize stiffness (minimize deflection) Support Structure Ken Youssefi Engineering 10, SJSU 4

Wind Turbine Structure Hollow tapered tube Lattice structure Hollow tube with guy wire Ken Youssefi Engineering 10, SJSU 5

Wind Turbine Structural support Tripod support Tube with guy wire and winch Ken Youssefi Engineering 10, SJSU 6

Harmful to birds and bats Ken Youssefi Engineering 10, SJSU 7

Wind Belt (50 W) 9600 KWh of energy annually Mariah Power's Windspire Magnetic Levitation wind-turbine Ken Youssefi Engineering 10, SJSU Helical wind turbine 8

Wind Turbine Structure World Trade Center in Bahrain Three giant wind turbine provides 15% of the power needed. Ken Youssefi Engineering 10, SJSU 9

Sunbathing on top of a wind turbine Sunbathing on top of a 200 -ft wind turbine Ken Youssefi Engineering 10, SJSU 10

Support structure failure, New York. Stress at the base of the support tower exceeding the strength of the material Ken Youssefi Engineering 10, SJSU 11

Support structure failure, Denmark. Caused by high wind Ken Youssefi Engineering 10, SJSU 12

Blade failure, Illinois. Failure at the thin section of the blade Support structure failure, UK Lightning strike, Germany Ken Youssefi Engineering 10, SJSU 13

Ken Youssefi Engineering 10, SJSU 14

Balsa wood Cardboard PVC Pipe Ken Youssefi Engineering 10, SJSU 15

Ken Youssefi Engineering 10, SJSU 16

X Ken Youssefi Engineering 10, SJSU 17

Provided Motor (generator), 1” diameter You design Blades Top plate to support the motor (wood, 3. 5 x 3. 5 inch) Support structure Bottom plate (wood, 12 x 12 inch) Ken Youssefi Engineering 10, SJSU 18

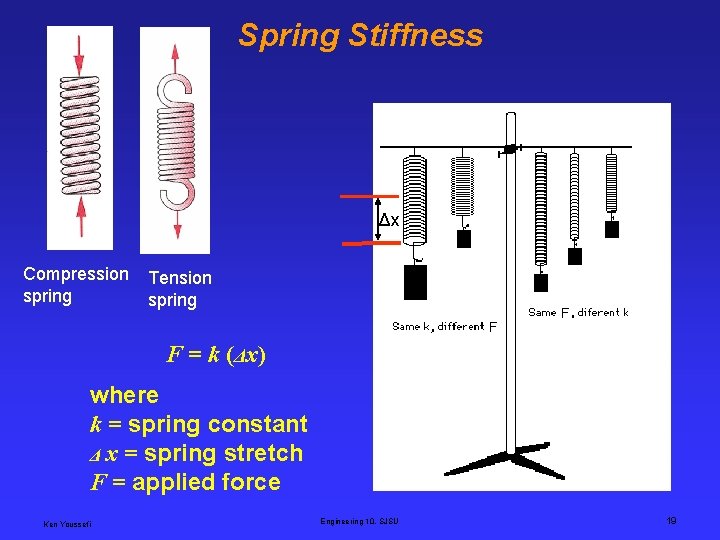
Spring Stiffness Δx Compression spring Tension spring F F F = k (Δx) where k = spring constant Δ x = spring stretch F = applied force Ken Youssefi Engineering 10, SJSU 19

Stiffness (Spring) • Deflection is proportional to load, F = k (∆x) Load (N or lb) slope, k Deflection (mm or in. ) Slope of Load-Deflection curve: The “Stiffness” Ken Youssefi Engineering 10, SJSU 20

Stiffness (Solid Bar) • Stiffness in tension and compression – Applied Forces F, length L, cross-sectional area, A, and material property, E (Young’s modulus) F F L F A End view F L δ E is constant for a given material E (steel) = 30 x 106 psi E (Al) = 10 x 106 psi Elongation (deflection) of the bar Ken Youssefi E (concrete) = 3. 4 x 103 psi 3 Stiffness for components E (Kevlar, plastic) = 19 x 10 psi in tension-compression E (rubber) = 100 psi Engineering 10, SJSU 21

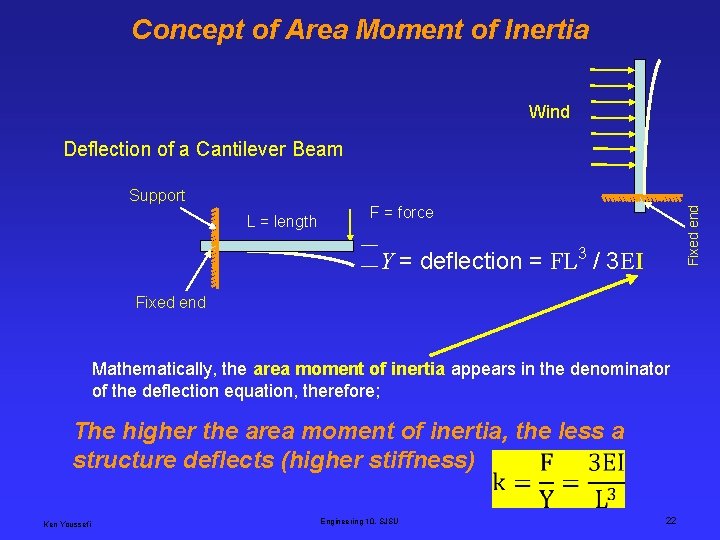
Concept of Area Moment of Inertia Wind Deflection of a Cantilever Beam L = length F = force Fixed end Support Y = deflection = FL 3 / 3 EI Fixed end Mathematically, the area moment of inertia appears in the denominator of the deflection equation, therefore; The higher the area moment of inertia, the less a structure deflects (higher stiffness) Ken Youssefi Engineering 10, SJSU 22

Wind Turbine Tower Stiffness Testing Dial indicator to measure deflection Pulley weights Ken Youssefi Engineering 10, SJSU 23

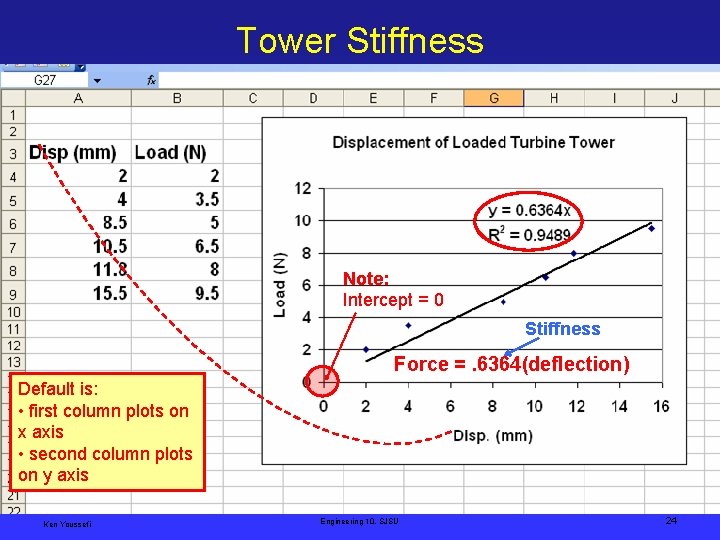
Tower Stiffness Note: Intercept = 0 Stiffness Force =. 6364(deflection) Default is: • first column plots on x axis • second column plots on y axis Ken Youssefi Engineering 10, SJSU 24

Concept of Area Moment of Inertia The Area Moment of Inertia is an important parameter in determine the state of stress in a part (component, structure), the resistance to bending and buckling, and the amount of deflection in a beam. The area moment of inertia allows you to tell how stiff a structure is. The Area Moment of Inertia, I, is a term used to describe the capacity of a cross-section (profile) to resist bending. It is always considered with respect to a reference axis, in the x or y direction. It is a mathematical property of a section concerned with a surface area and how that area is distributed about the reference axis. The reference axis is usually a centroidal axis. Y = deflection = FL 3 / 3 EI Ken Youssefi Engineering 10, SJSU 25

Moment of Inertia – Comparison Y = deflection = FL 3 / 3 EI 1 Load 4” Maximum distance of 4 inch to the centroid 2 x 8 beam I 1 2” Same load and location centroidal axis I 2 2 1” 2 x 8 beam Maximum distance of 1 inch to the centroidal axis Stiffer beam I 2 > I 1 , orientation 2 deflects less Ken Youssefi Engineering 10, SJSU 26

I-Beam and C-Channel Ken Youssefi Engineering 10, SJSU 27

Mathematical Equation for Area Moment of Inertia Ixx = ∑ (Ai) (yi)2 = A 1(y 1)2 + A 2(y 2)2 + …. . An(yn)2 A (total area) = A 1 + A 2 + ……. . An A 2 A 1 y 2 X Ken Youssefi Area, A X Engineering 10, SJSU 28

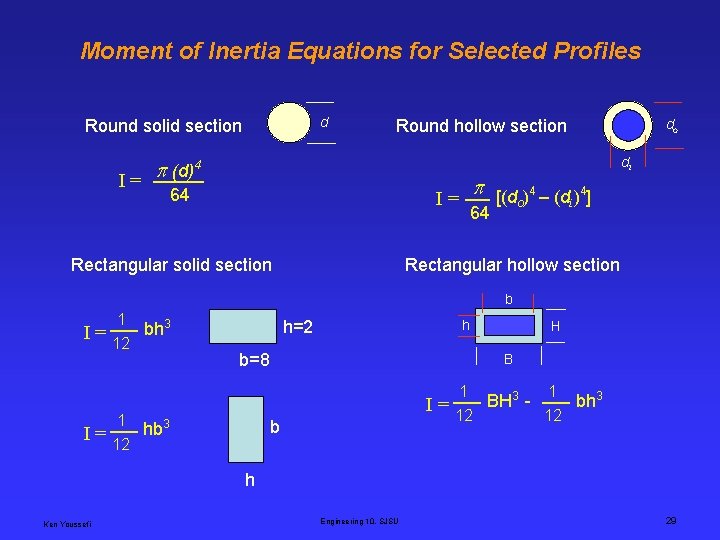
Moment of Inertia Equations for Selected Profiles d Round solid section I= Round hollow section do di (d)4 64 I= Rectangular solid section [(d )4 – (d )4] o i 64 Rectangular hollow section b I= I= 1 bh 3 12 h=2 h b=8 B I= 1 hb 3 12 H b 1 1 BH 3 bh 3 12 12 h Ken Youssefi Engineering 10, SJSU 29

Example – Optimization for Weight & Stiffness Consider a solid rectangular section 2. 0 inch wide by 1. 0 high. 1. 0 I = (1/12)bh 3 = (1/12)(2)(1)3 =. 1667 , Area = 2 2. 0 Now, consider a hollow rectangular section 2. 25 inch wide by 1. 25 high by. 125 thick. b B = 2. 25, H = 1. 25 h b = 2. 0, h = 1. 0 H B I = (1/12)(2. 25)(1. 25)3 – (1/12)(2)(1)3=. 3662 -. 1667 =. 1995 Area = 2. 25 x 1. 25 – 2 x 1 =. 8125 (. 1995 -. 1667)/(. 1667) x 100 = 20% less deflection Compare the weight of the two parts (same material and length), so only the cross sectional areas need to be compared. (2 -. 8125)/(2) =. 6 = 60% lighter So, for a slightly larger outside dimension section, 2. 25 x 1. 25 instead of 2 x 1, you can design a beam that is 20% stiffer and 60 % lighter Ken Youssefi Engineering 10, SJSU 30

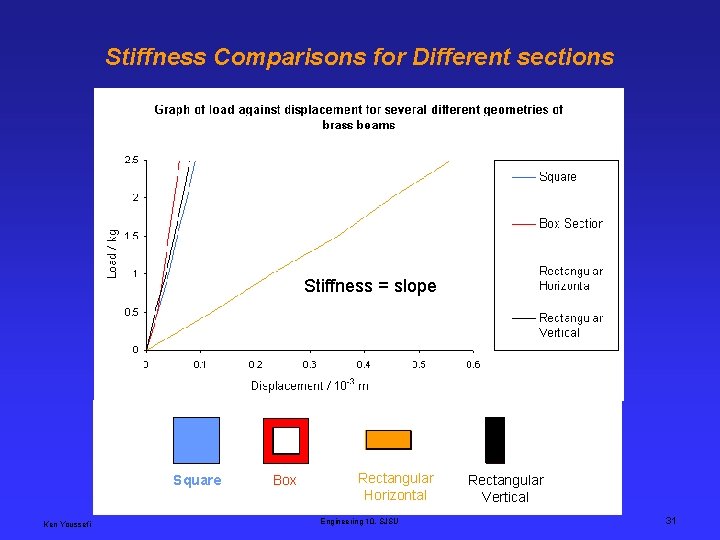
Stiffness Comparisons for Different sections Stiffness = slope Square Ken Youssefi Box Rectangular Horizontal Engineering 10, SJSU Rectangular Vertical 31

Material and Stiffness E = Elasticity Module, a measure of material deformation under a load. Deflection of a Cantilever Beam Support L = length F = force Y = deflection = FL 3 / 3 EI Fixed end The higher the value of E, the less a structure deflects (higher stiffness) Ken Youssefi Engineering 10, SJSU 32

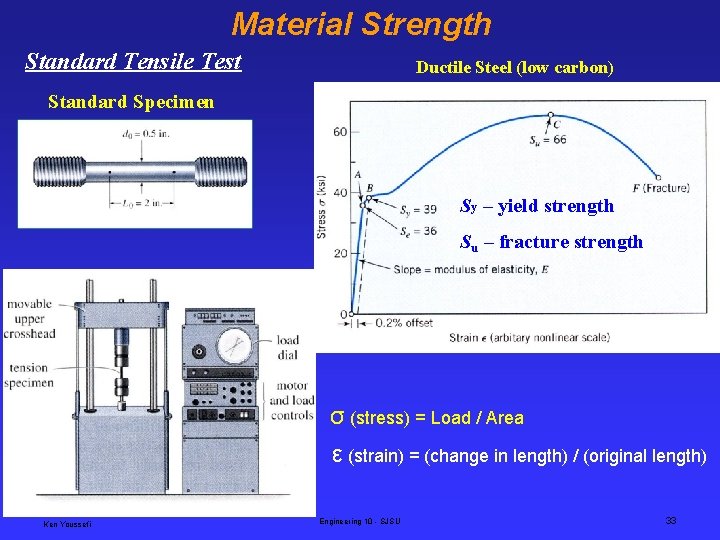
Material Strength Standard Tensile Test Ductile Steel (low carbon) Standard Specimen Sy – yield strength Su – fracture strength σ (stress) = Load / Area ε (strain) = (change in length) / (original length) Ken Youssefi Engineering 10 - SJSU 33

Common Mechanical Properties • Yield Strength (Sy) – the highest stress a material can withstand still return exactly to its original size when unloaded. • Ultimate Strength (Su) - the greatest stress a material can withstand, fracture stress. • Modulus of elasticity (E) - the slope of the straight portion of the stress-strain curve. • Ductility - the extent of plastic deformation that a material undergoes before fracture, measured as a percent elongation of a material. % elongation = (final length, at fracture – original length) / original length • Resilience - the capacity of a material to absorb energy within the elastic zone (area under the stress-strain curve in the elastic zone) • Toughness - the total capacity of a material to absorb energy without fracture (total area under the stress-strain curve) Ken Youssefi Engineering 10 - SJSU 34

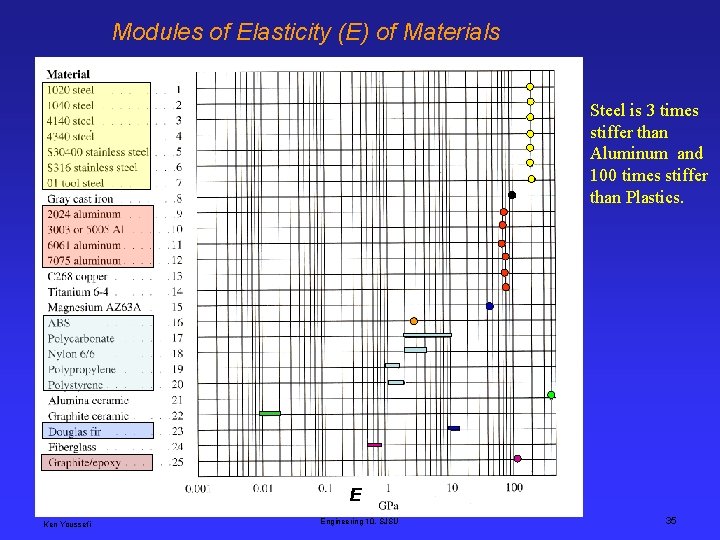
Modules of Elasticity (E) of Materials Steel is 3 times stiffer than Aluminum and 100 times stiffer than Plastics. E Ken Youssefi Engineering 10, SJSU 35

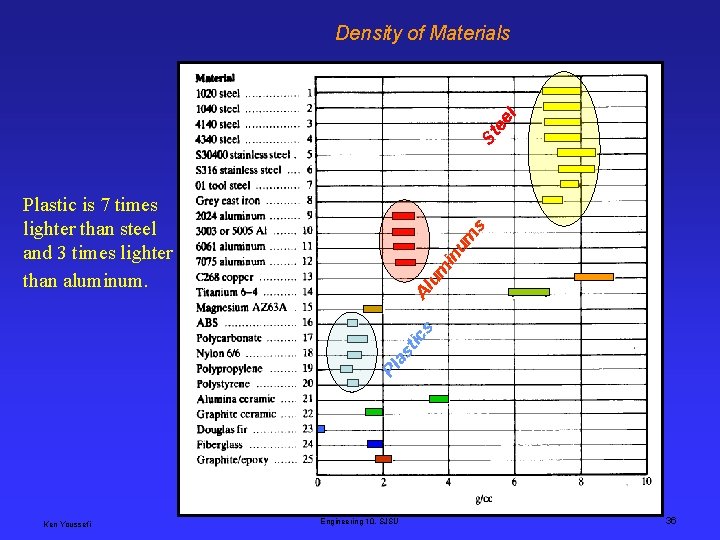
St ee l Density of Materials Pl as tic s Al um in u m s Plastic is 7 times lighter than steel and 3 times lighter than aluminum. Ken Youssefi Engineering 10, SJSU 36

Stiffness Testing Apparatus Successful testers Ken Youssefi Engineering 10, SJSU 37