Wind loading and structural response Lecture 12 Dr

Wind loading and structural response Lecture 12 Dr. J. D. Holmes Along-wind dynamic response

Dynamic response • Significant resonant dynamic response can occur under wind actions for structures with n 1 < 1 Hertz (approximate) • All structures will experience fluctuating loads below resonant frequencies (background response) • Significant resonant response may not occur if damping is high enough • e. g. electrical transmission lines - ‘pendulum’ modes - high aerodynamic damping

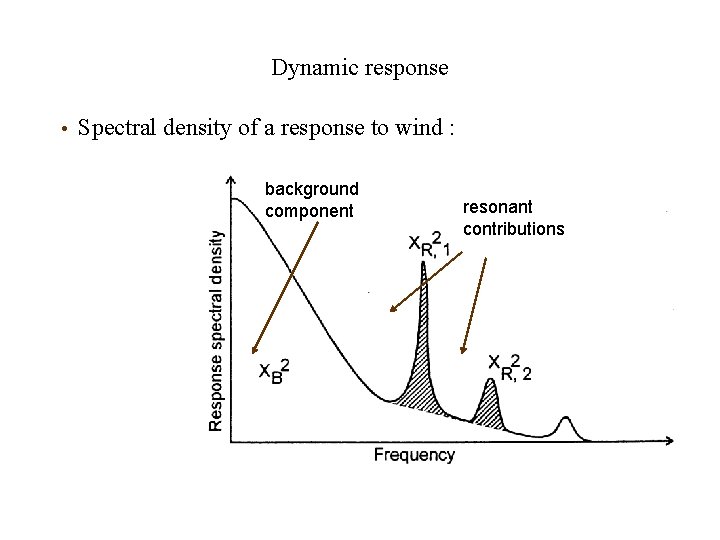
Dynamic response • Spectral density of a response to wind : background component resonant contributions

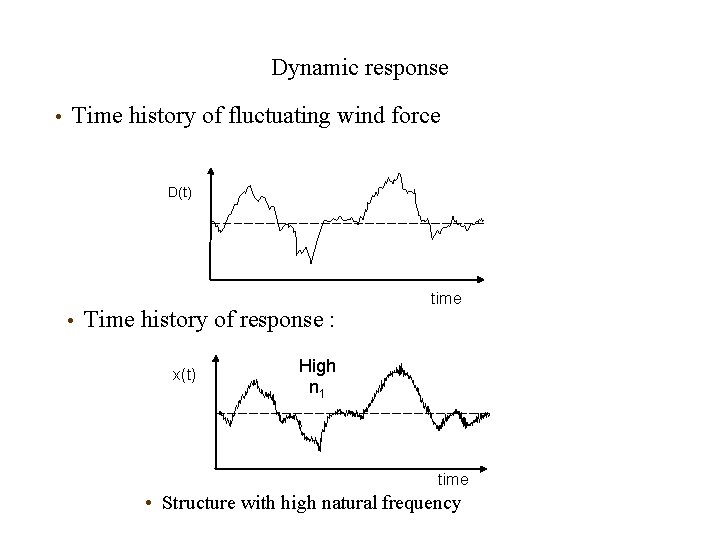
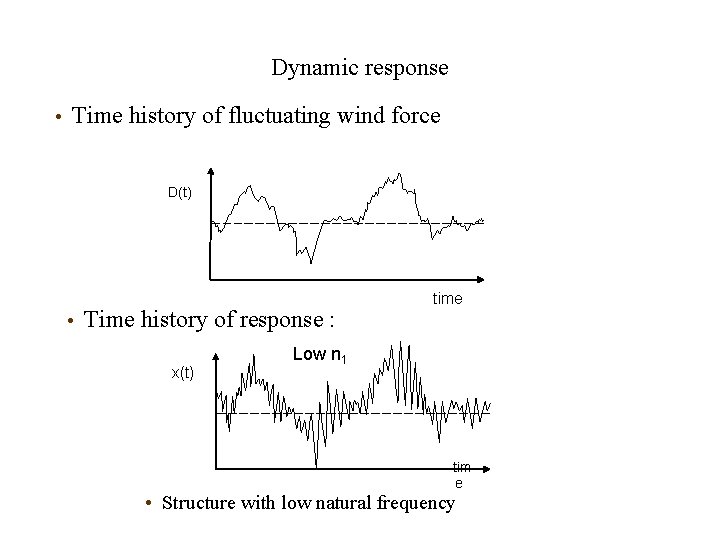
Dynamic response • Time history of fluctuating wind force D(t) time

Dynamic response • Time history of fluctuating wind force D(t) • Time history of response : x(t) time High n 1 time • Structure with high natural frequency

Dynamic response • Time history of fluctuating wind force D(t) • Time history of response : x(t) time Low n 1 tim e • Structure with low natural frequency

Dynamic response • Features of resonant dynamic response : • Time-history effect : when vibrations build up structure response at any given time depends on history of loading • Additional forces resist loading : inertial forces, damping forces • Stable vibration amplitudes : damping forces = applied loads inertial forces (mass acceleration) balance elastic forces in structure effective static loads : ( 1 times) inertial forces

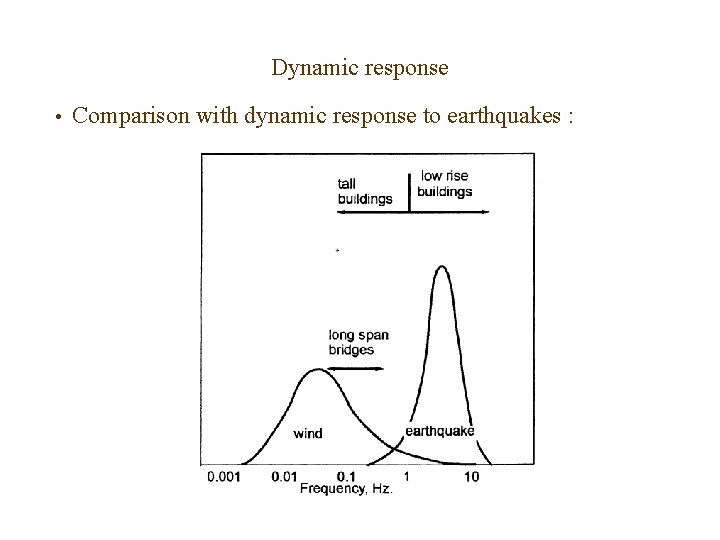
Dynamic response • Comparison with dynamic response to earthquakes : • Earthquakes are shorter duration than most wind storms • Dominant frequencies of excitation in earthquakes are 10 -50 times higher than wind loading • Earthquake forces appear as fully-correlated equivalent lateral forces wind forces (along-wind and cross wind) are partially-correlated fluctuating forces

Dynamic response • Comparison with dynamic response to earthquakes :

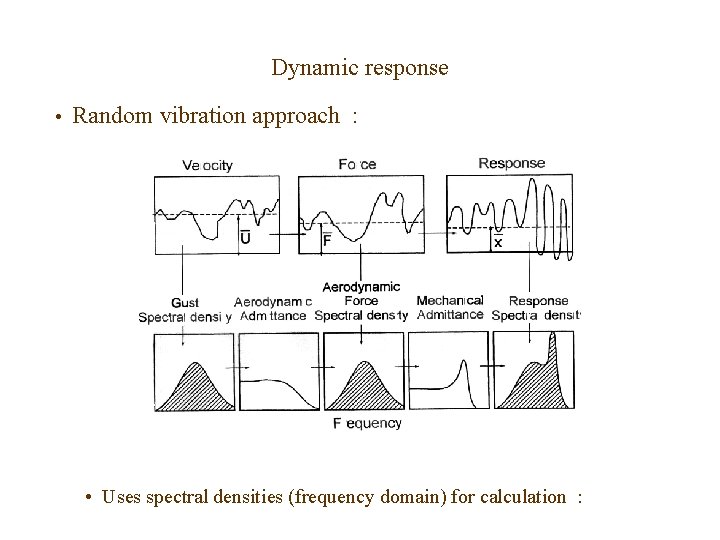
Dynamic response • Random vibration approach : • Uses spectral densities (frequency domain) for calculation :

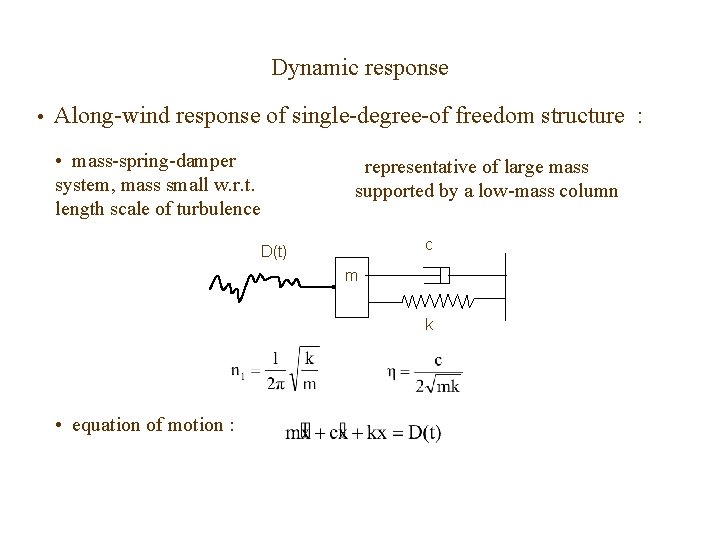
Dynamic response • Along-wind response of single-degree-of freedom structure : • mass-spring-damper system, mass small w. r. t. length scale of turbulence representative of large mass supported by a low-mass column c D(t) m k • equation of motion :

Dynamic response • Along-wind response of single-degree-of freedom structure : • by quasi-steady assumption (Lecture 9) : since : • in terms of spectral density : • hence : this is relation between spectral density of force and velocity

Dynamic response • Along-wind response of single-degree-of freedom structure : • deflection : X(t) = X + x'(t) mean deflection : k = spring stiffness spectral density : where the mechanical admittance is given by : this is relation between spectral density of deflection and approach velocity

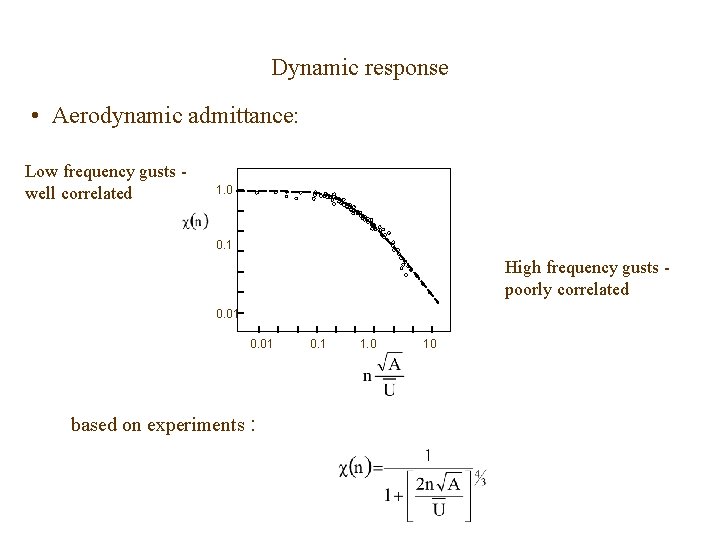
Dynamic response • Aerodynamic admittance: • Larger structures - velocity fluctuations approaching windward face cannot be assumed to be uniform then : where 2(n) is the ‘aerodynamic admittance’

Dynamic response • Aerodynamic admittance: Low frequency gusts well correlated 1. 0 0. 1 High frequency gusts poorly correlated 0. 01 based on experiments : 0. 1 1. 0 10

Dynamic response • Aerodynamic admittance: hence : substituting D = k X :

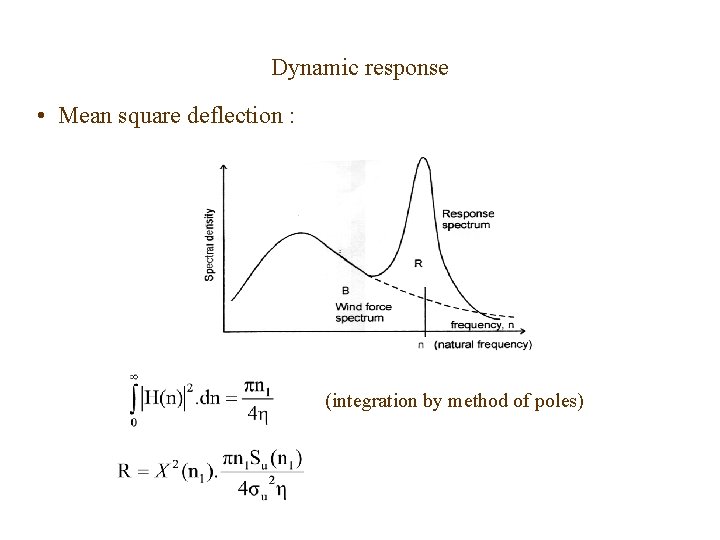
Dynamic response • Mean square deflection : where : independent of frequency assumes X 2(n) and Su(n) are constant at X 2(n 1) and Su(n 1), near the resonant peak

Dynamic response • Mean square deflection : (integration by method of poles)

Dynamic response • Gust response factor (G) : Expected maximum response in defined time period / mean response in same time period g = peak factor = ‘cycling’ rate (average frequency)

Dynamic response • Dynamic response factor (Cdyn): This is a factor defined as follows : Maximum response including correlation and resonant effects / maximum response excluding correlation and resonant effects B = 1 (reduction due to correlation ignored) R = 0 (resonant effects ignored) Used in codes and standards based on peak gust (e. g. ASCE-7)

Dynamic response • Gust effect factor (ASCE-7) : For flexible and dynamically sensitive structures (Section 6. 5. 8. 2) This is a ‘dynamic response factor’ not a ‘gust response factor’ 0. 925(instead of 1) is ‘calibration factor’ 1. 7 (instead of 2) to adjust for 3 -second gust instead of true peak gust Separate peak factors (g. Q and g. R) for background and resonant response : g. Q = gv= 3. 4

Dynamic response • Gust effect factor (ASCE-7) : Resonant response factor (Equation 6 -8) : Previously : is critical damping ratio ( ) Rh. RB(0. 53 + 0. 47 RL) is the aerodynamic admittance 2(n 1) decomposed into components for vertical separations (Rh), lateral separations (RB) and along-wind (windward/ leeward wall) (RL)

Dynamic response • Gust effect factor (ASCE-7) : Rn should be : In fact it is : where : Note that : 6. 9=(2/3) 10. 3 so that Note that Su(0) is equal to 6. 9 u 2 Lz/Vz But Su(0) should = 4 u 2 lu / Uz (Lecture 7) Hence Lz = (4/6. 9) lu = 0. 58 lu

Dynamic response • Along-wind response of structure with distributed mass : The calculation of along-wind response with distributed masses (many modes of vibration) is more complex (Section 5. 3. 6 in the book) Based on modal analysis (Lecture 11) : x(z, t) = j aj (t) j (z) is mode shape in jth mode Use : generalized (modal) mass, stiffness, damping, applied force for each mode Two approaches : i) use modal analysis for background and resonant parts (inefficient needs many modes) - Section 5. 3. 6 ii) calculate background component separately; use modal analysis only for resonant parts - Section 5. 3. 7 Easier to use (ii) in the context of effective static load distributions

End of Lecture 12 John Holmes 225 -405 -3789 JHolmes@lsu. edu