Wind loading and structural response Lecture 11 Dr

Wind loading and structural response - Lecture 11 Dr. J. D. Holmes Basic structural dynamics II

Basic structural dynamics II • Topics : • multi-degree-of freedom structures - free vibration • multi-degree-of freedom structures - forced vibration • response of a tower to vortex shedding forces

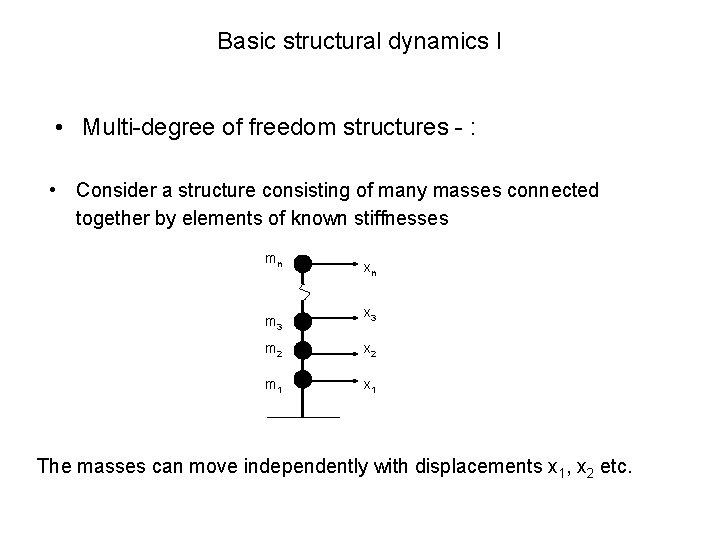
Basic structural dynamics I • Multi-degree of freedom structures - : • Consider a structure consisting of many masses connected together by elements of known stiffnesses mn m 3 xn x 3 m 2 x 2 m 1 x 1 The masses can move independently with displacements x 1, x 2 etc.

Basic structural dynamics I • Multi-degree of freedom structures – free vibration : • Each mass has an equation of motion For free vibration: mass m 1: mass m 2: …………. mass mn: Note coupling terms (e. g. terms in x 2, x 3 etc. in first equation) stiffness terms k 12, k 13 etc. are not necessarily equal to zero

Basic structural dynamics I • Multi-degree of freedom structures – free vibration : In matrix form : Assuming harmonic motion : {x }= {X}sin( t+ ) This is an eigenvalue problem for the matrix [k]-1[m]

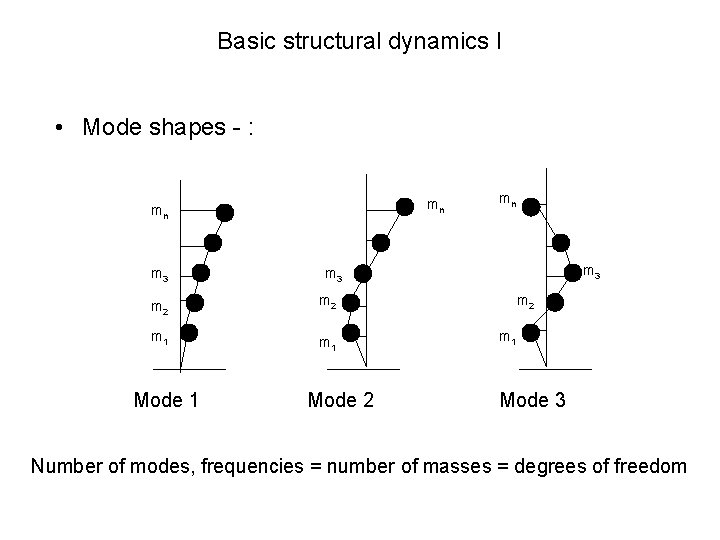
Basic structural dynamics I • Multi-degree of freedom structures – free vibration : There are n eigenvalues, j and n sets of eigenvectors { j} for j=1, 2, 3 ……n Then, for each j : j is the circular frequency (2 nj); { j} is the mode shape for mode j. They satisfy the equation : The mode shape can be scaled arbitrarily - multiplying both sides of the equation by a constant will not affect the equality

Basic structural dynamics I • Mode shapes - : mn mn m 3 m 3 m 2 m 1 Mode 1 mn Mode 2 m 1 Mode 3 Number of modes, frequencies = number of masses = degrees of freedom

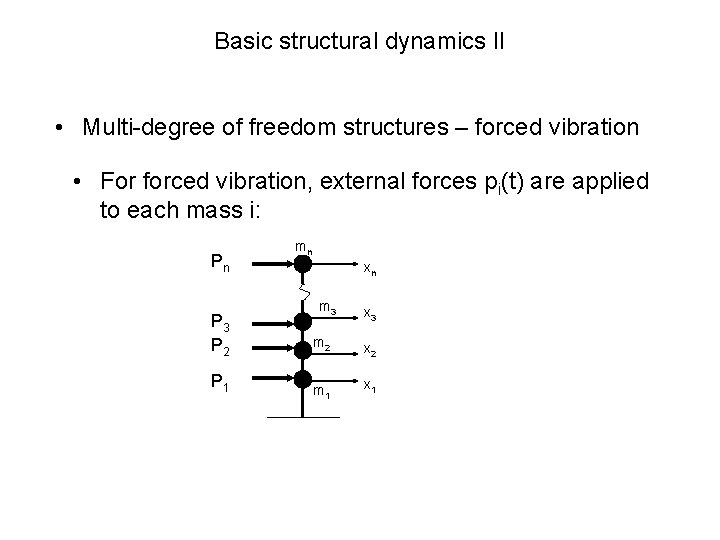
Basic structural dynamics II • Multi-degree of freedom structures – forced vibration • For forced vibration, external forces pi(t) are applied to each mass i: Pn mn xn m 3 x 3 P 2 m 2 x 2 P 1 m 1 x 1

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration • For forced vibration, external forces pi(t) are applied to each mass i: …………. • These are coupled differential equations of motion

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration • For forced vibration, external forces pi(t) are applied to each mass i: …………. • These are coupled differential equations

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration • For forced vibration, external forces pi(t) are applied to each mass i: …………. • These are coupled differential equations

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration • In matrix form : Mass matrix [m] is diagonal Stiffness matrix [k] is symmetric {p(t)} is a vector of external forces – each element is a function of time

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration • Modal analysis is a convenient method of solution of the forced vibration problem when the elements of the stiffness matrix are constant – i. e. the structure is linear The coupled equations of motion are transformed into a set of uncoupled equations Each uncoupled equation is analogous to the equation of motion for a single d-o-f system, and can be solved in the same way

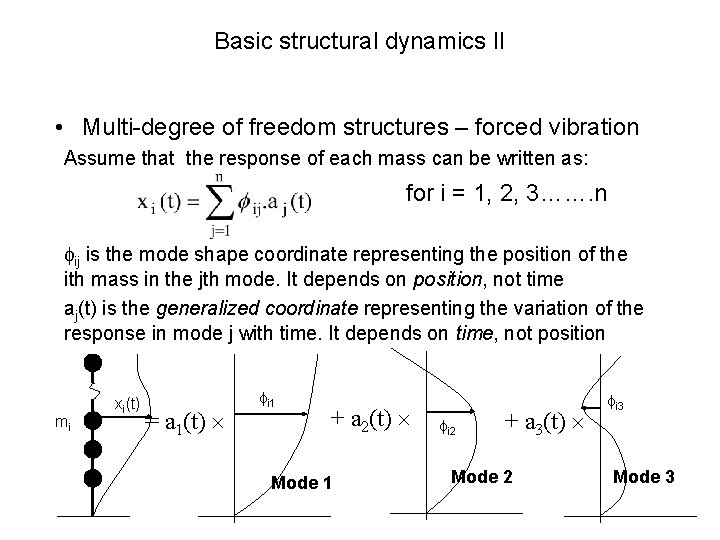
Basic structural dynamics II • Multi-degree of freedom structures – forced vibration Assume that the response of each mass can be written as: for i = 1, 2, 3……. n ij is the mode shape coordinate representing the position of the ith mass in the jth mode. It depends on position, not time aj(t) is the generalized coordinate representing the variation of the response in mode j with time. It depends on time, not position mi xi(t) = a 1(t) i 1 + a 2(t) Mode 1 i 2 + a 3(t) Mode 2 i 3 Mode 3

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration In matrix form : [ ] is a matrix in which the mode shapes are written as columns ([ ]T is a matrix in which the mode shapes are written as rows) Differentiating with respect to time twice :

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration By substitution, the original equations of motion reduce to: The matrix [G] is diagonal, with the jth term equal to : Gj is the generalized mass in the jth mode The matrix [K] is also diagonal, with the jth term equal to :

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration The right hand side is a single column, with the jth term equal to : Pj(t) is the generalized force in the jth mode

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration We now have a set of independent uncoupled equations. Each one has the form : Gen. mass This is the same in form as the equation of motion of a single d. o. f. system, and the same solutions for aj(t) can be used

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration We now have a set of independent uncoupled equations. Each one has the form : Gen. stiffness This is the same in form as the equation of motion of a single d. o. f. system, and the same solutions for aj(t) can be used

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration We now have a set of independent uncoupled equations. Each one has the form : Gen. force This is the same in form as the equation of motion of a single d. o. f. system, and the same solutions for aj(t) can be used

Basic structural dynamics II • Multi-degree of freedom structures – forced vibration We now have a set of independent uncoupled equations. Each one has the form : Gen. coordinate This is the same in form as the equation of motion of a single d. o. f. system, and the same solutions for aj(t) can be used

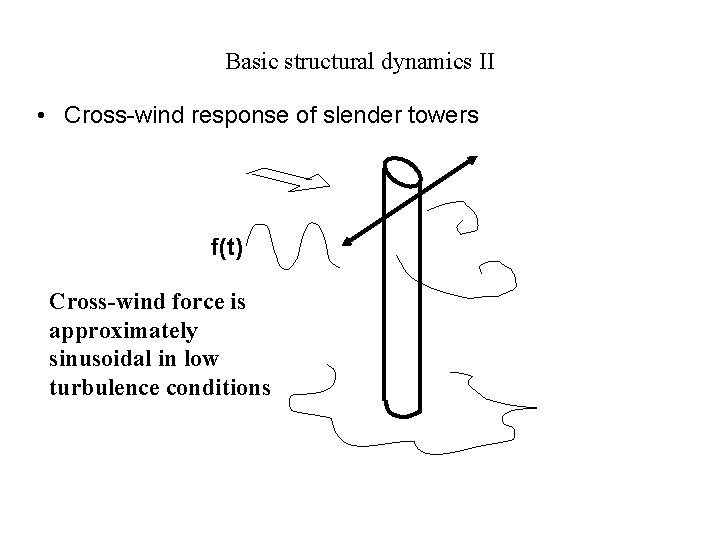
Basic structural dynamics II • Cross-wind response of slender towers f(t) Cross-wind force is approximately sinusoidal in low turbulence conditions

Basic structural dynamics II • Cross-wind response of slender towers Sinusoidal excitation model : Assumptions : • sinusoidal cross-wind force variation with time • full correlation of forces over the height • constant amplitude of fluctuating force coefficient ‘Deterministic’ model - not random Sinusoidal excitation leads to sinusoidal response (deflection)

Basic structural dynamics II • Cross-wind response of slender towers Sinusoidal excitation model : Equation of motion (jth mode): Gj is the ‘generalized’ or effective mass = j(z) is mode shape Pj(t) is the ‘generalized’ or effective force =

Basic structural dynamics II • Cross-wind response of slender towers Sinusoidal excitation model : Applied force is assumed to be sinusoidal with a frequency equal to the vortex shedding frequency, ns Maximum amplitude occurs at resonance when ns=nj Force per unit length of structure = Cl = cross-wind (lift) force coefficient b = width of tower

Basic structural dynamics II • Cross-wind response of slender towers Then generalized force in jth mode is : Pj, max is the amplitude of the sinusoidal generalized force

Basic structural dynamics II • Cross-wind response of slender towers Then, maximum amplitude Note analogy with single d. o. f system result (Lecture 10) Substituting for Pj, max : Then, maximum deflection on structure at height, z, (Slide 14 - considering only 1 st mode contribution)

Basic structural dynamics II • Cross-wind response of slender towers Maximum deflection at top of structure (Section 11. 5. 1 in ‘Wind Loading of Structures’) where j is the critical damping ratio for the jth mode, equal to Strouhal Number for vortex shedding ze = effective height ( 2 h/3) (Scruton Number or mass-damping parameter) m = average mass/unit height

End of Lecture John Holmes 225 -405 -3789 JHolmes@lsu. edu