William Stallings Computer Organization and Architecture Chapter 9

William Stallings Computer Organization and Architecture Chapter 9 Computer Arithmetic Rev. by Luciano Gualà (2008) 8 - 1

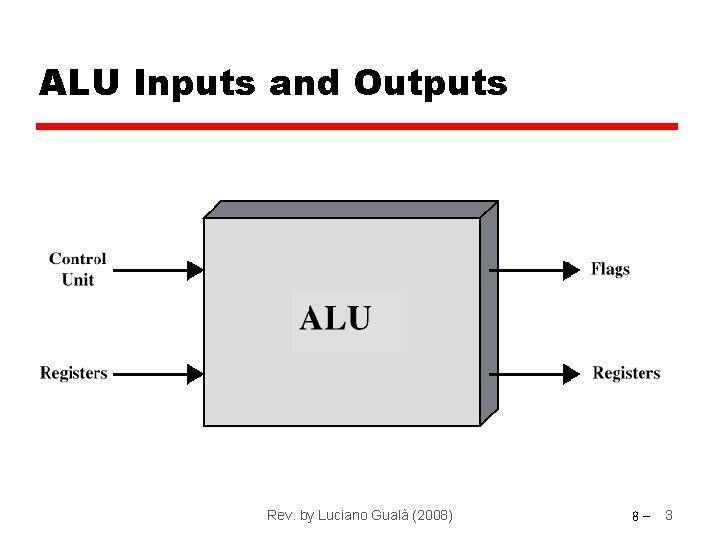
Arithmetic & Logic Unit • Does the calculations • Almost everything else in the computer is there to service this unit • Handles integers • May handle floating point (real) numbers Rev. by Luciano Gualà (2008) 8 - 2

ALU Inputs and Outputs Rev. by Luciano Gualà (2008) 8 - 3

Reminder • Let A=an-1 an-2…a 1 a 0 be a (pure) binary number • Its (decimal) value is: Example: 10010 = 24 + 21 = 16 + 2 = 18 Rev. by Luciano Gualà (2008) 8 - 4

Integer Representation • Only have 0 & 1 to represent everything • Positive numbers stored in binary § e. g. 41=00101001 § Binary digit = Bit • No minus sign • Negative integer representations: § Sign-Magnitude § Two’s complement Rev. by Luciano Gualà (2008) 8 - 5

Sign-Magnitude • Left most bit is sign bit • 0 means positive • 1 means negative +18 = 00010010 -18 = 10010010 • Problems § Need to consider both sign and magnitude in arithmetic § Two representations of zero (+0 and -0) Rev. by Luciano Gualà (2008) 8 - 6

A better representation: Two’s Complement • Let A=an-1 an-2…a 1 a 0 be a n-length binary string • It’s value is in Two’s Complement representation is: if an-1=0 then A is a non-negative number if an-1=1 then A is a negative number Rev. by Luciano Gualà (2008) 8 - 7

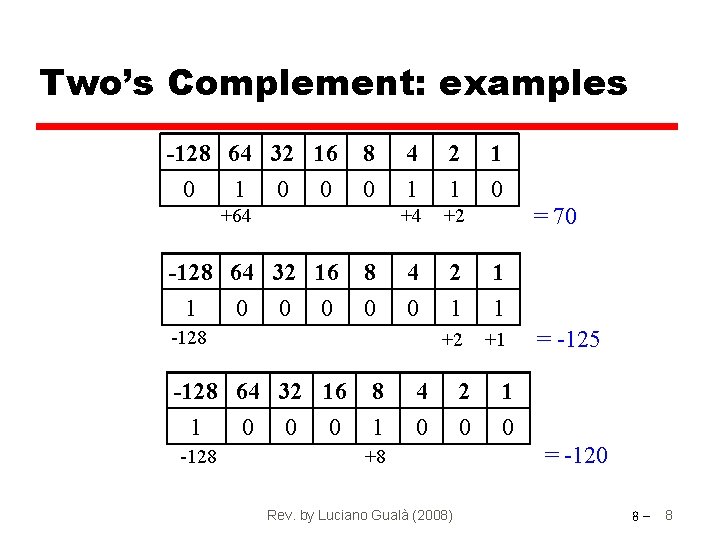
Two’s Complement: examples -128 64 32 16 0 1 0 0 8 4 2 1 0 1 1 0 +4 +2 8 4 2 1 0 0 1 1 +2 +1 +64 -128 64 32 16 1 0 0 0 -128 64 32 16 1 -128 0 0 0 = 70 8 4 2 1 1 0 0 0 +8 Rev. by Luciano Gualà (2008) = -125 = -120 8 - 8

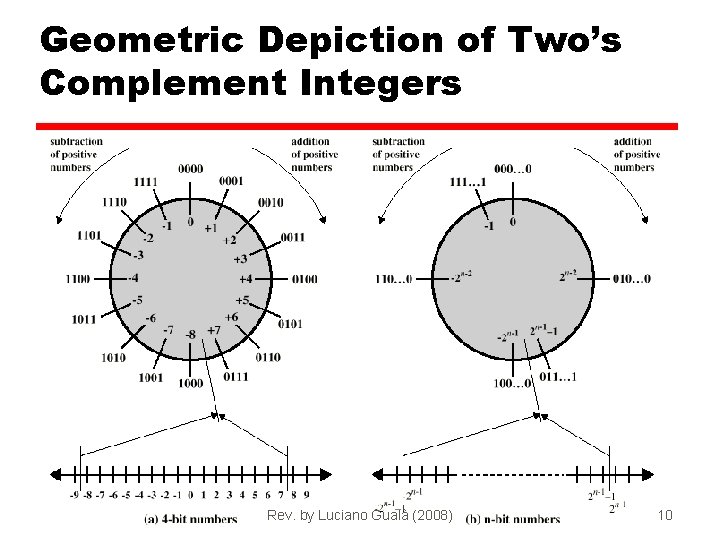
Benefits • Only one representation of zero +0 +1 +2 +3 +4 +5 +6 +7 = = = = 0000 0001 0010 0011 0100 0101 0110 0111 -1 -2 -3 -4 -5 -6 -7 -8 = = = = 1111 1110 1101 1100 1011 1010 1001 1000 • Arithmetic works easily (see later) Rev. by Luciano Gualà (2008) 8 - 9

Geometric Depiction of Two’s Complement Integers Rev. by Luciano Gualà (2008) 8 - 10

Range of Numbers • 8 bit 2’s complement +127 = 01111111 = 27 -1 -128 = 10000000 = -27 • 16 bit 2’s complement +32767 = 01111111 = 215 - 1 -32768 = 10000000 = -215 Rev. by Luciano Gualà (2008) 8 - 11

2’s Complement representation for negative numbers • To represent a negative number using the “two’s complement” technique: 1. First decide how many bits are used for representation 2. Then write the modulo of the negative number (in pure binary) 3. Then, change each 0 in 1, each 1 in 0 (Boolean Complement or “one’s complement”) 4. Finally, add 1 (as the result of Step 3 was a pure binary number) Rev. by Luciano Gualà (2008) 8 - 12

Examples • E. g. : how to represent -3 with 4 bits: § Start from +3 = 0011 § Boolean complement gives § Add 1 to LSB gives -3 • Represent -20 with 8 bits: § Start from +20 = § Bolean complement gives § Add 1 1100 1101 00010100 11101011 11101100 • Negation works in the same way, e. g. negation of -3 is obtained by the “two’s complement” of -3: § Representation of -3 § Boolean complement gives § Add 1 to LSB gives -(-3)=+3 1101 0010 0011 Rev. by Luciano Gualà (2008) 8 - 13

Negation Special Case 1 • • • 0= 0000 Bitwise NOT 1111 (Boolean complement) Add 1 to LSB +1 Result 1 0000 Carry is ignored, so: - 0 = 0 OK ! Rev. by Luciano Gualà (2008) 8 - 14

Negation Special Case 2 • • -8 = 1000 Bitwise NOT 0111 (Boolean complement) Add 1 to LSB +1 Result 1000 So: -(-8) = -8 WRONG ! Monitor MSB (sign bit) If it does not change during negation there is a mistake (but for 0!) Rev. by Luciano Gualà (2008) 8 - 15

Conversion Between Lengths • Positive number: pack with leading zeroes +18 = 00010010 +18 = 0000 00010010 • Negative number: pack with leading ones -18 = 1110 -18 = 1111 1110 • i. e. pack with MSB (sign bit) Rev. by Luciano Gualà (2008) 8 - 16

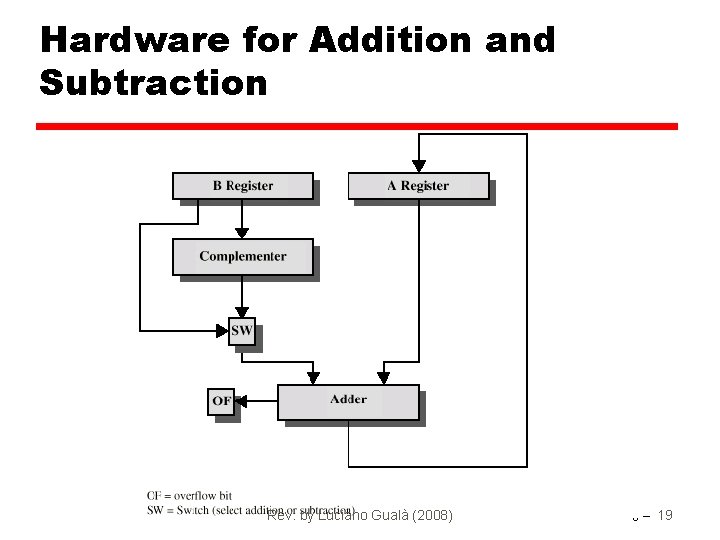
Addition and Subtraction • Addition: standard • Overflow: when the result needs more bits to be represented • Monitor MSB: if it changes there may be an overflow § When Pos + Pos or Neg + Neg the sign bit should not change: if it does there is an overflow • Subtraction: take two’s complement of subtrahend add to minuend § i. e. : a - b = a + (-b) • So we only need addition and complement circuits Rev. by Luciano Gualà (2008) 8 - 17

Addition: examples 1001 + -7 0101 = 5 1110 -2 1100 + 0100 = 1 0000 0011 + 0100 = 0111 0101 + 0100 = 1001 3 4 7 -4 4 0 5 4 overflow Rev. by Luciano Gualà (2008) 1100 + -4 1111 = -1 -5 1 1011 1001 + -7 1010 = -6 overflow 1 0011 8 - 18

Hardware for Addition and Subtraction Rev. by Luciano Gualà (2008) 8 - 19

Real Numbers • …very informally, numbers with the fractional point • Actually, only finite precision real numbers • we need to code the binary point position • Solution: floating point numbers Rev. by Luciano Gualà (2008) 8 - 20

Reminder • Let A=an-1 an-2…a 1 a 0 , a-1, a-2, …, a-m be a binary number • Its value is: Example: 1001, 1011 = 23 + 20 +2 -1 + 2 -3 + 2 -4 =9, 6875 2 -1 2 -2 2 -3 2 -4 2 -5 0, 250 0, 125 0, 0625 0, 03125 Rev. by Luciano Gualà (2008) 8 - 21

Real Numbers • Where is the binary point? § Fixed? • Very limited § Moving? • How do you show where it is? • Example: 976. 000 = 9, 76 * 1014 0, 0000000976 = 9, 76 * 10 -14 Rev. by Luciano Gualà (2008) 8 - 22

Sign bit Floating Point Biased Exponent Significand or Mantissa • Represents the value +/-. <significand> * <base><exponent> • “Floating” refers to the fact that the true position of the point “floats” according to the value of the exponent Rev. by Luciano Gualà (2008) 8 - 23

Normalization (10, 0101)2= 10, 0101* 20 = 10010, 1 * 2 -3 = 1001010 * 2 -5 = 0, 00100101 * 24 • Floating Point numbers are usually normalized § exponent is adjusted so that there is a single bit equal to 1 before the binary point • Similar to scientific notation for decimal numbers where numbers are normalized to give a single digit before the decimal point 3123 = 3. 123 x 103 Rev. by Luciano Gualà (2008) 8 - 24

Normalization • A normalized number ( 0) has the following form: +/- 1, bbb…b * 2 +/- E where b {0, 1} • The base (or radix) for the exponent is suppose to be 2 (so it is not represented) • Since MSB of the mantissa is always 1 there is no need to represent it Rev. by Luciano Gualà (2008) 8 - 25

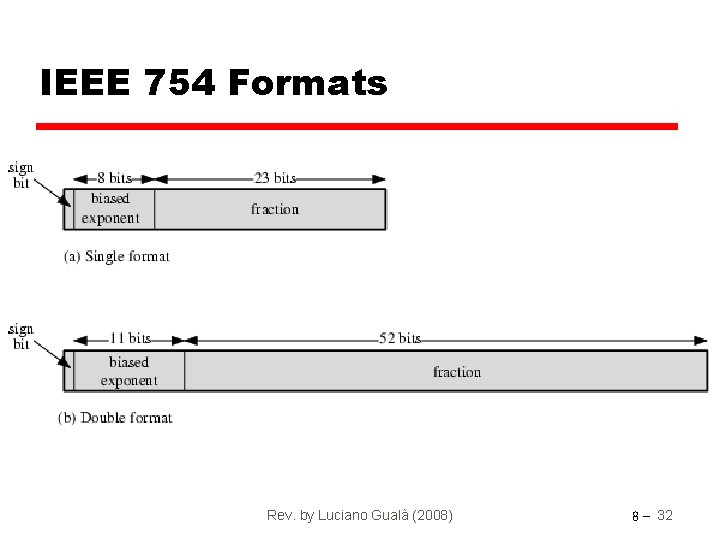
Typical Representation of Floating Point with 32 bits • Mantissa uses 23 bits to store a 24 bits pure binary number in the interval [1, 2) • Sign is stored in the first bit • Exponent value is represented in excess or biased notation with 8 bits • Excess (bias) 127 means § § 8 bit exponent field Nominal exponent value has range 0 -255 Subtract 127 (= 28 -1 -1) to get correct exponent value Real range of exponent value is -127 to +128 Rev. by Luciano Gualà (2008) 8 - 26

excess (bias) notation • Two parameters are specified: § the number of bits n § the bias value K (usually, K=2 n -1 -1) • the string consisting of all 0 s represents the value –K • the string consisting of all 1 s represents the value –K + 2 n-1 n = 4 K=7 0000 = -7 0001 = -6 0010 = -5 0011 = -4 0100 = -3 0101 = -2 0110 = -1 0111 = 0 Rev. by Luciano Gualà (2008) 1000 = 1001 = 1010 = 1011 = 1100 = 1101 = 1110 = 1111 = 1 2 3 4 5 6 7 8 8 - 27

Floating Point Examples 147 = 127+20 107 = 127 -20 Rev. by Luciano Gualà (2008) 8 - 28

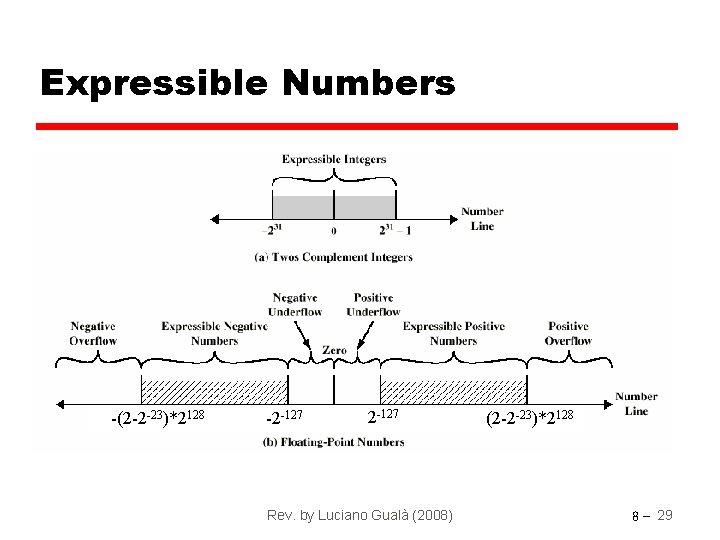
Expressible Numbers -(2 -2 -23)*2128 -2 -127 Rev. by Luciano Gualà (2008) (2 -2 -23)*2128 8 - 29

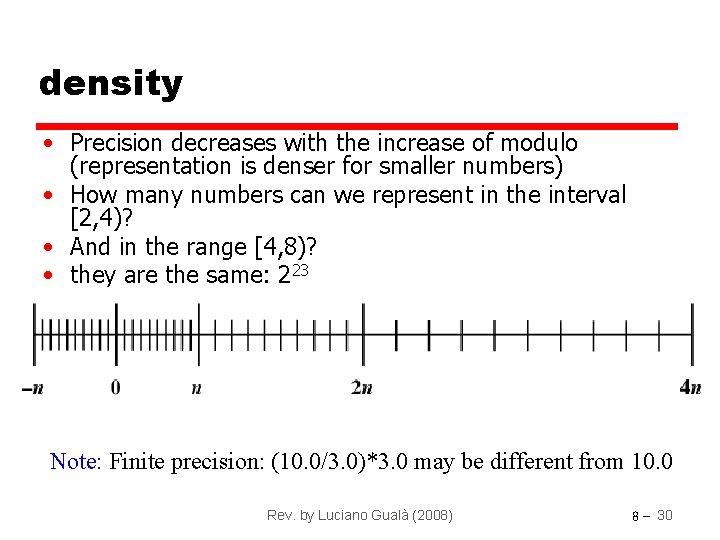
density • Precision decreases with the increase of modulo (representation is denser for smaller numbers) • How many numbers can we represent in the interval [2, 4)? • And in the range [4, 8)? • they are the same: 223 Note: Finite precision: (10. 0/3. 0)*3. 0 may be different from 10. 0 Rev. by Luciano Gualà (2008) 8 - 30

IEEE 754 • • Standard for floating point storage 32 and 64 bit standards 8 and 11 bit exponent respectively Extended formats (both mantissa and exponent) for intermediate results Rev. by Luciano Gualà (2008) 8 - 31

IEEE 754 Formats Rev. by Luciano Gualà (2008) 8 - 32

Special cases (single format) • exponent [-126, 127]: normalized numbers • Some strings are interpreted as special strings • Two representations for zero (posit. and negat. ) § +/- 0 = 0/1 0000000000000000 • Able to represent infinity (posit. and negat. ) § +/- = 0/1 1111 000000000000 • Non-normalized numbers: § 0/1 0000 (string different to all 0 s) § exponent=-126 § form of significand: 0. bbbb. . • NAN = Not A Number § Result of an operation which has no solution § Propagated as NAN through subsequent operations § representation: 0/1 1111 (string different to all 0 s) Rev. by Luciano Gualà (2008) 8 - 33

FP Arithmetic: addition and subtraction • • Check for zero Align significands (adjusting exponents) Add or subtract significands Normalize result Rev. by Luciano Gualà (2008) 8 - 34

FP Arithmetic: multiplication and division • • • Check for zero Add/subtract exponents Multiply/divide significands (watch sign) Normalize Round All intermediate results should be in double length storage Rev. by Luciano Gualà (2008) 8 - 35