William M Trochim James P Donnelly Kanika Arora

William M. Trochim James P. Donnelly Kanika Arora 12 Inferential Analysis

12. 1 Foundations of Analysis for Research Design • The analysis procedure you choose is based on your research design • All of the procedures in this chapter are based on the General Linear Model (GLM) – A system of equations that is used as the mathematical framework for most of the statistical analyses used in applied social research

12. 2 Inferential Statistics • Statistical analyses used to reach conclusions that extend beyond the immediate data alone • The GLM uses dummy variables – A variable that uses discrete numbers, usually 0 and 1, to represent different groups in your study

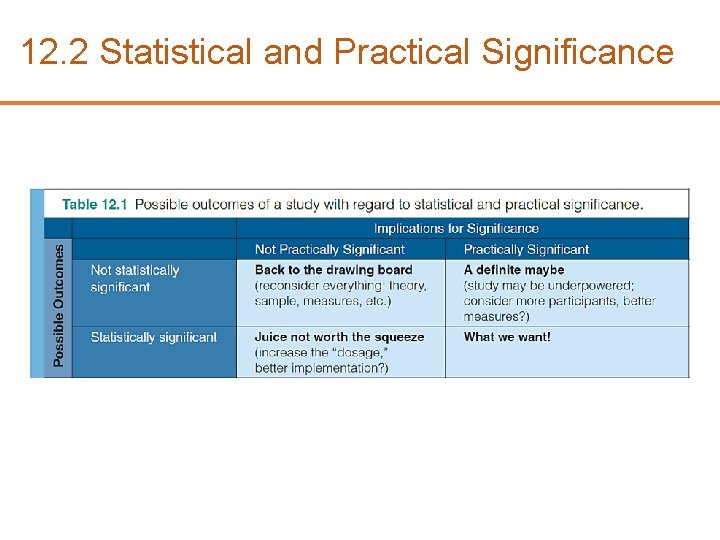
12. 2 Inferential Statistics – Statistical Significance • Uses the GLM to estimate statistical significance – p value: an estimate of the probability of your result if the null hypothesis is true – Statistical significance is not enough; we need an effect size, as well

12. 2 Statistical and Practical Significance

12. 3 General Linear Model • Foundation for – t-test – ANOVA and ANCOVA – Regression, factor, and cluster analyses – Multidimensional scaling – Discriminant function analysis – Canonical correlation

12. 3 General Linear Model • Assumptions – The relationships between variables are linear – Samples are random and independently drawn from the population – Variables have equal (homogeneous) variances – Variables have normally distributed error

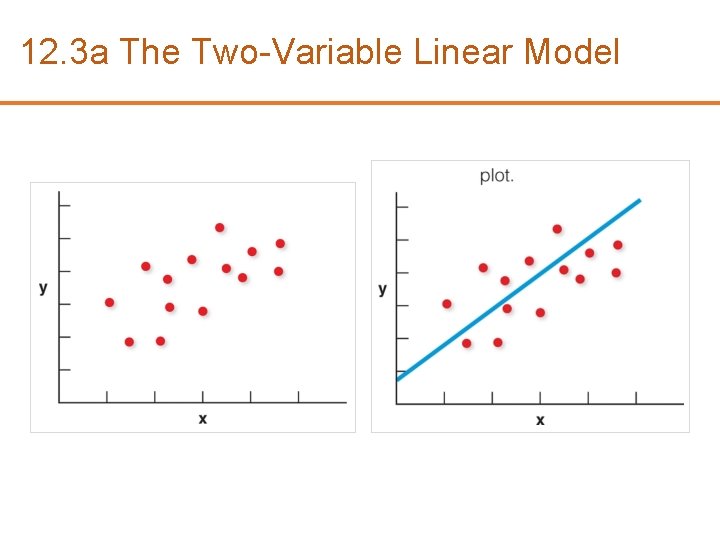
12. 3 a The Two-Variable Linear Model

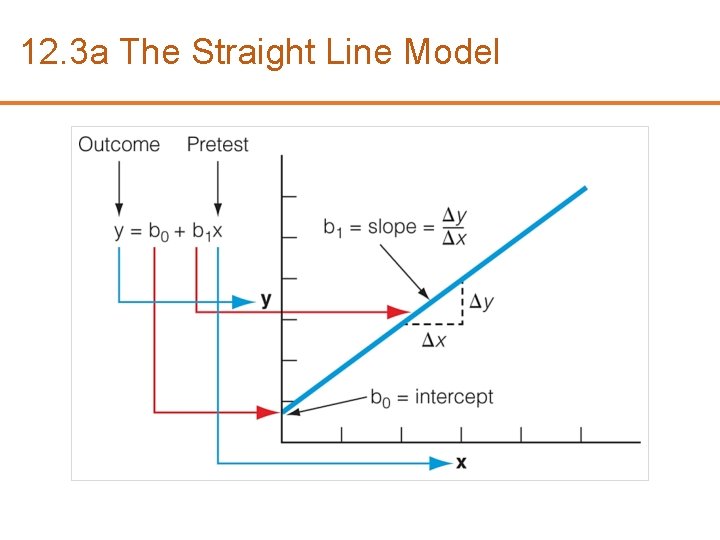
12. 3 a The Straight Line Model

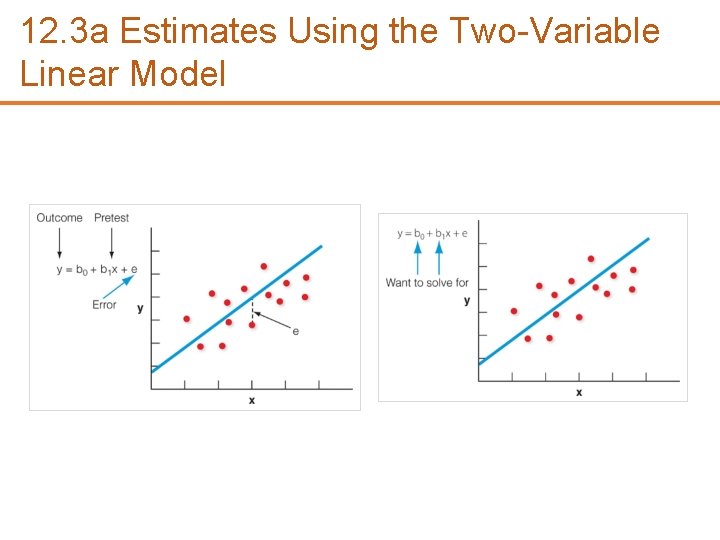
12. 3 a Estimates Using the Two-Variable Linear Model

12. 3 b The “General” in the General Linear Model

12. 3 b The “General” in the General Linear Model (cont’d. ) • The GLM allows you to summarize a wide variety of research outcomes • The major problem for the researcher who uses the GLM is model specification – How to identify the equation that best summarizes the data for a study – If the model is misspecified, the estimates of the coefficients (the b-values) that you get from the analysis are likely to be biased

12. 3 c Dummy Variables • Enable you to use a single regression equation to represent multiple groups – Act like switches that turn various values on and off in an equation

12. 3 c Using Dummy Variables

12. 3 d The t-Test • Assesses whether the means of two groups (for example, the treatment and control groups) are statistically different from each other

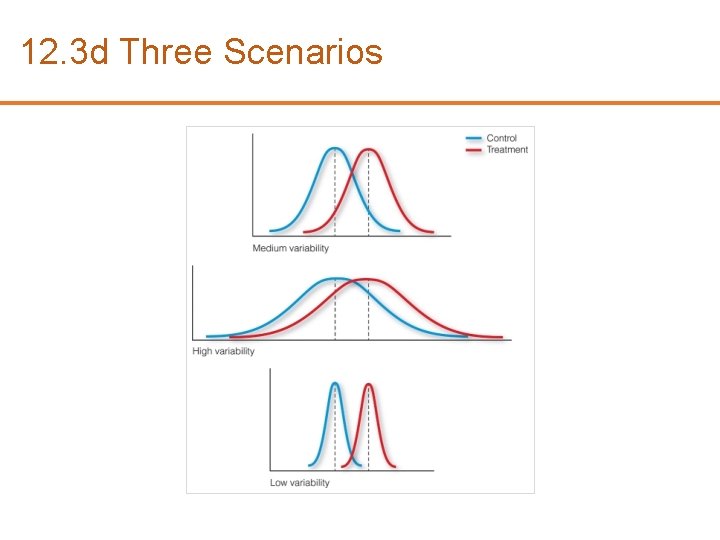
12. 3 d Three Scenarios

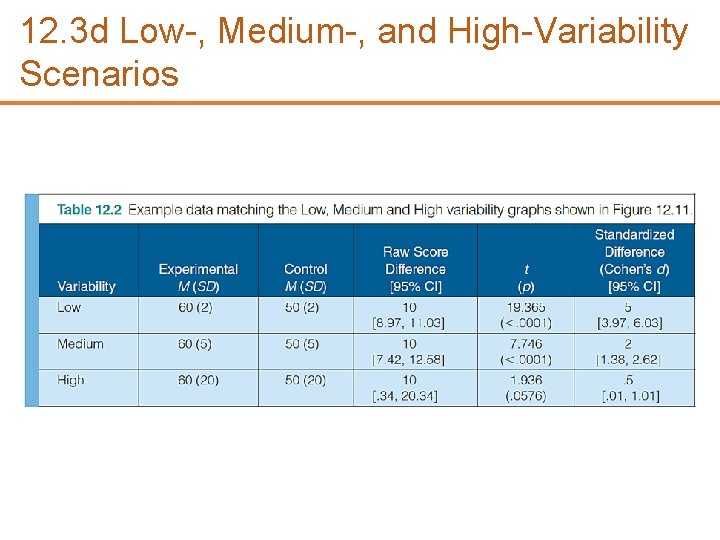
12. 3 d Low-, Medium-, and High-Variability Scenarios

12. 3 d Difference Between the Means • When you are looking at the differences between scores for two groups, you have to judge the difference between their means relative to the spread or variability of their scores • The t-test does just this—it determines if a difference exists between the means of two groups

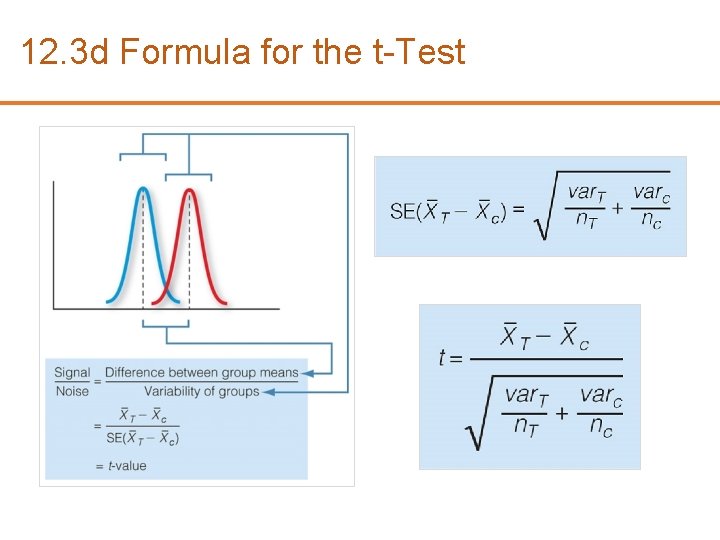
12. 3 d Formula for the t-Test

12. 3 d The t-Test • t-Value • Standard error of the difference • Variance • Standard deviation (sd) • Alpha level (α) • Degrees of freedom (df) The regression formula for the t-test & ANOVA

12. 4 a The Two-Group Posttest-Only Randomized Experiment • Meets the following requirements: – Has two groups – Uses a post-only measure – Has a distribution for each group on the response measure, each with an average and variation – Assesses treatment effect as the statistical (non-chance) difference between the groups

12. 4 a The Two-Group Posttest-Only Randomized Experiment (cont’d. ) • Three tests meet these requirements, and they all yield the same results – Independent t-Test – One-way ANOVA – Regression analysis

12. 4 b Factorial Design Analysis • Analysis requires results for two main effects and one interaction effect in a 2 x 2 factorial design

12. 4 c Randomized Block Analysis • The dummy variable Z 1 represents the treatment group • The other dummy variables indicate the blocks • The beta values (Β) reflect the analogous treatment and blocks

12. 4 d Analysis of Covariance • An analysis that estimates the difference between the groups on the posttest after adjusting for differences on the pretest

12. 5 Quasi-Experimental Analysis • Quasi-experimental designs still use the GLM, but it has to be adjusted for measurement error – Any influence on an observed score not related to what you are attempting to measure • This adjustment for error makes the analyses more complicated

12. 5 a Nonequivalent Groups Analysis Formula for adjusting pretest values for unreliability in the reliabilitycorrected ANCOVA The regression model for the reliability corrected ANCOVA

12. 5 b Regression-Discontinuity Analysis Adjusting the pretest by subtracting the cutoff in the Regression. Discontinuity (RD) analysis model. The regression model for the basic regression-discontinuity design

12. 5 c Regression Point Displacement Analysis

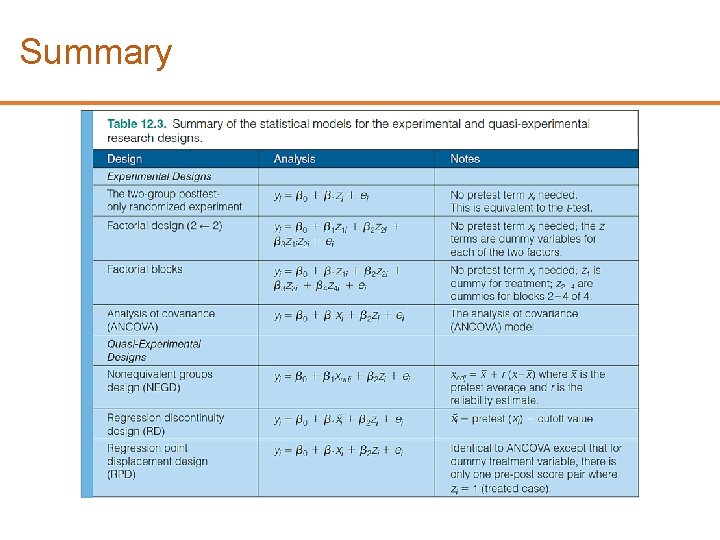
Summary

Discuss and Debate • What is the difference between statistical significance and practical significance? – Give an example to support your answer • Discuss how the four assumptions underlying the GLM impact the data analysis process